因子分析在SPSS软件中的数据应用解析

肖志芳

作为一项可以从多个变量中抽取共性因子的统计分析技术，因子分析能够揭示复杂又庞大的变量之间的关系，能够从可观测的多个变量中归纳总结出较少个数的因子，以便进行最大程度、最有效的解释并概括这些观测变量的信息，从而计算出事物之间的相关性。

1 因子分析的实例应用

本文选取了J 市某高校关于大学生学习倦怠的调查数据，拟对该份数据使用SPSS 应用分析，在对该调查数据进行SPSS 标准化数据处理后如表1所示。该调查数据共有16 个变量，其中T01=我能精力充沛地学习，T02=我不知道该干什么，T03=我很想放弃学习，T04=我在学习中经常能够达到所制定的目标，T05=我在一天的学习结束后感到非常疲劳，T06=学不学我都无所谓，T07=我学习时忘记一切，T08=我最近学习精疲力尽，T09=学习体会不到成就，T10=学习对我没有意义，T11=我能够很好地应付考试，T12=我上课感觉很累，T13=无所谓的态度学习，T14=我有效地解决学习中的问题，T15=我可以做到轻松地应对学习方面的问题，T16=对于所学知识我可以很好掌握。本案例拟从这16 个变量中归纳出较少数量的因子，以便进行有针对性的分析问题、解决问题。

在进行因子分析之前，需要对SPSS 中的因子载荷、因子的方差贡献以及公因子方差等作用进行一些了解[1]。要理解因子载荷的绝对值与其相关性成正比趋势[2]。公因子方差也称为变量共同度，公因子的方差值与变量（T01～T16）被解释度成正比趋势，越是无限接近于1，越可以被所选的公因子说明。同理，因子的方差贡献亦是如此。

根据SPSS 分析对应的相关矩阵表中的相关系数反映了T01～T16 之间相互依赖的程度。从该矩阵中可以看出T01～T16 间的相关系数较大，且对应的显著性普遍偏小，说明变量T01～T16 之间存在显著相关性，因而有必要对这16 个变量进行因子分析。

根据本调查数据量表分析，如果KMO 统计量为（0.9～1），说明此份调查数据量表非常适合做因子分析，做因子分析的适合性随着KMO 统计量的值递减逐渐递减，KMO 统计量在0.7 以上时，表示该调查数据量表比较适合做因子分析，当该调查数据量表的KMO 统计量低于0.5 时，表示极不适合做因子分析[3]。通过KMO 与Bartlett 检验得到该份调查数据量表的KMO 统计量Kaiser-Meyer-Olkin=0.909，大于0.9，说明该调查表的相关矩阵中存在着共同的因子，非常适合进行因子分析，如表2 所示。

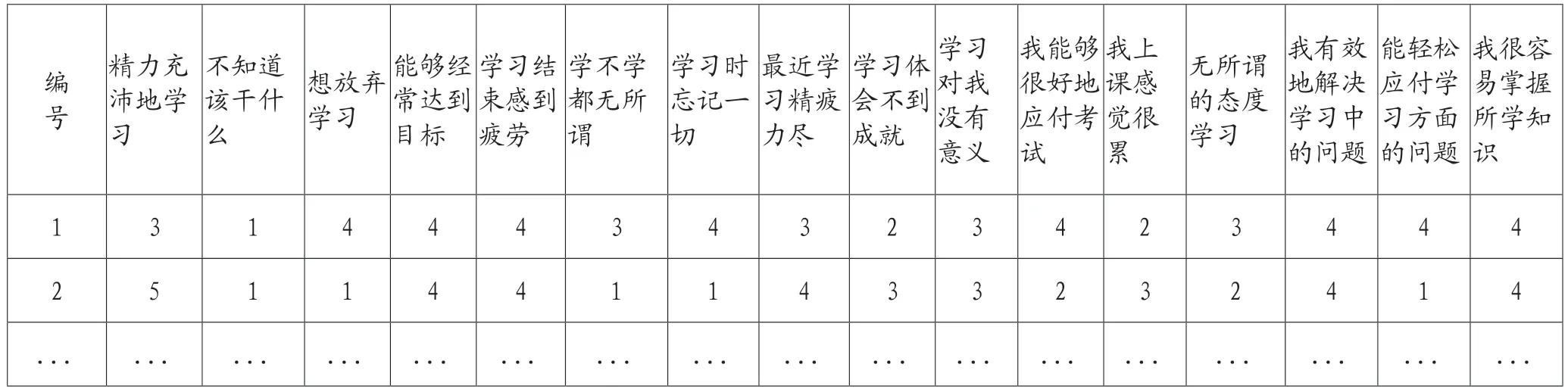
表1 原始数据表

表2 KMO 和 Bartlett的检验值

根据SPSS 运行后解释的总方差结果呈现，如表3 所示。可以分析出前三个因子的解释的累计方差58.278%，而后面的13 个公因子的特征值相对偏小，因此提取前三个公因子比较合适，它们可以较好地代表J 市某高校大学生学习倦怠的调查数据中T01～T16 所能反映出来的信息。与此同时，根据SPSS 分析的初始特征值栏中的合计列，如表4 所示。可以观察到从第四个公因子开始，其后的特征值变化趋缓，所以选前三个因子比较合适。

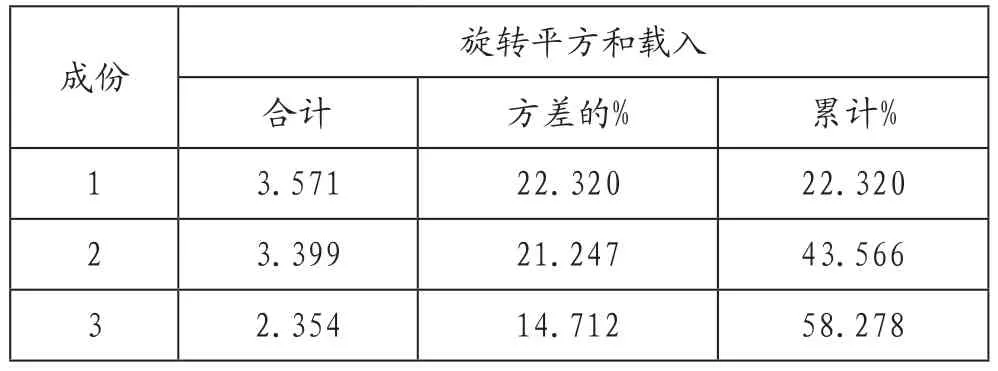
表3 解释的总方差

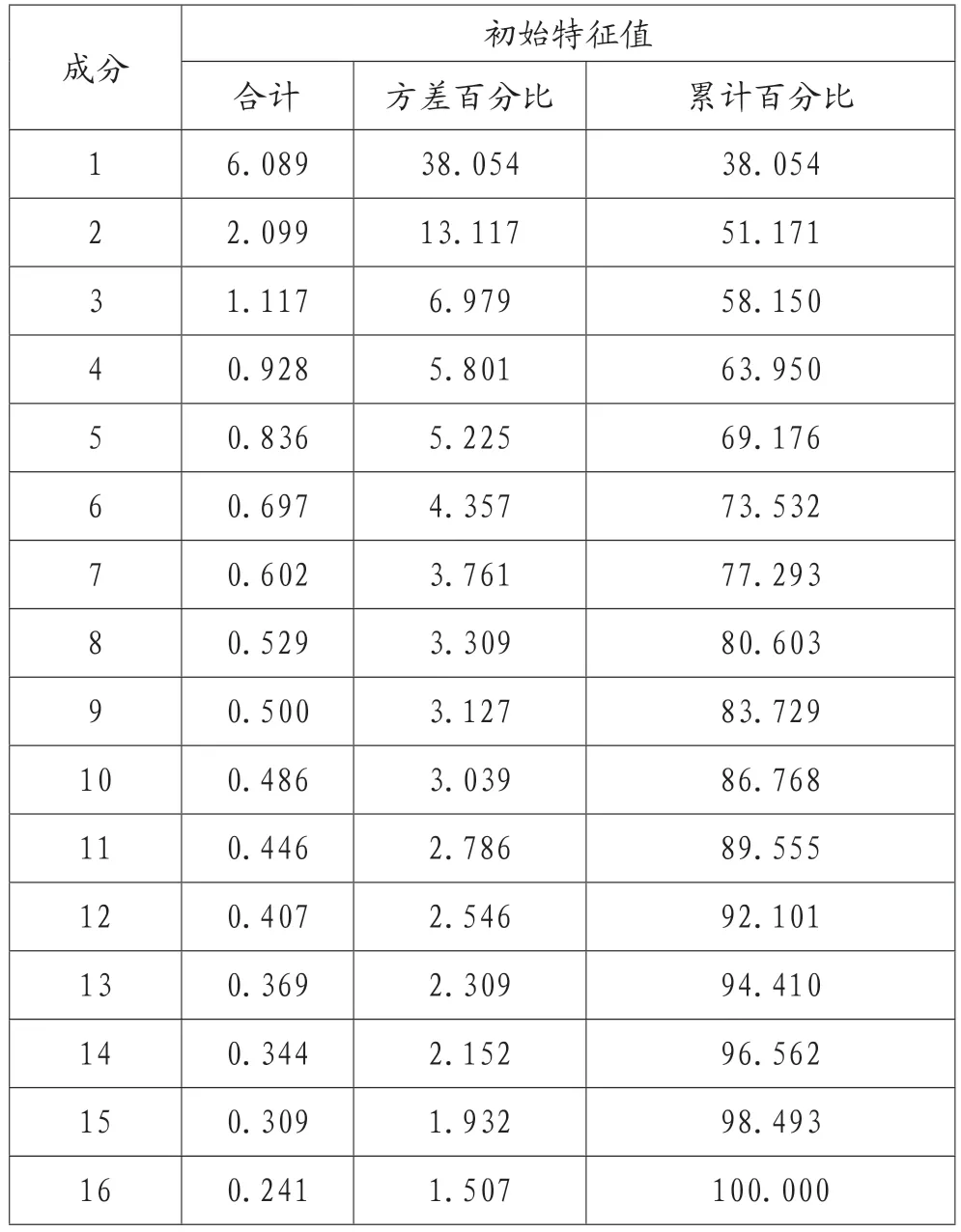
表4 初始特征值

为了更突出各个因子的典型代表变量，这样更容易发觉因子的作用.对因子进行旋转，旋转后比旋转前更容易解释各因子的意义。根据旋转成分矩阵中因子的载荷绝对值的大小，可以分析出有三个比较清晰的因子，分别为T01、T04、T07、T14、T15、T16，T03、T06、T09、T10、T13，T05、T08、T12，如表5 所示。

表5 旋转成分矩阵

2 结论

通过对该份调查数据的计算分析，提取出了J市某高校大学生学习倦怠的公共因子。分别为三个因子F1、F2、F3 进行命名，对F1 命名为：学业低成就感，对F2 命名为：学业疏离感，对F3 命名为：学业身心耗竭。因子分析反映了一种降维的思想。通过对16 个变量进行降维将关联度较高的变量汇集在一起，从而对该高校关于大学生学习倦怠的调查数据进行精简，进而降低问题分析的复杂性。