某履带装甲车辆传动齿轮系疲劳载荷研究

魏领军，刘海鸥，陈慧岩，石 锋

（1.北京理工大学，北京 100081；2.北京交通运输职业学院，北京 102611；3.中国汽车工程研究院，重庆 401122）

在现代军事战争中，履带装甲车辆良好的越野性能使其在陆军地面武器中具有不可替代的作用[1]。随着现代新技术的发展，履带装甲车辆通常把传动、操纵、转向、制动、液压控制系统集成一体，即综合传动系统[2]。传动齿轮系作为综合传动系统的核心部件，其编谱技术的研究与产品设计息息相关，并涉及多种学科和领域，准确的载荷谱在强度研究及产品设计中是必不可少的，所以传动齿轮系载荷谱研究具有十分重要的实用价值[3]。鉴于传动齿轮系载荷谱在指导试验和设计方面的重要作用，国内外众多行业都把其列为高密级的重点研究课题，研究成果极少对外公开[4]。

我国对履带装甲车辆传动齿轮系转矩测试数据有一定的积累，但未形成完整、规范的转矩载荷谱，传动齿轮系设计基本上是根据经验估计转矩载荷条件，与实际转矩载荷情况有一定差距，导致了传动齿轮系过设计或使用过程中出现传动齿轮断裂等问题，制约了我国履带装甲车辆综合传动技术的发展[5]。为了进一步提升我国履带装甲车辆传动系统的设计和试验验证能力，逐步实现由基于静载荷的安全系数法向基于载荷谱的疲劳设计法转变，对于实车传动齿轮系载荷编谱技术的研究是十分必要的[6]。

1 峰值计数技术

LMS TecWare的峰值计数原理如图1所示，其实质是统计随机时域数据的载荷极大值和极小值的分布。

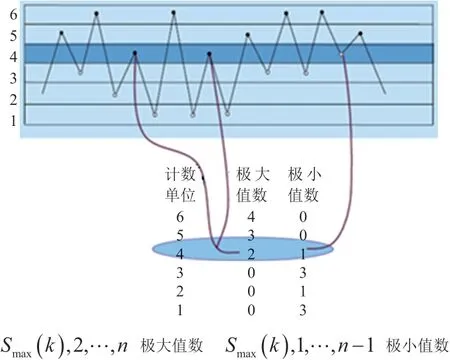
图1 峰值计数技术原理

把试验修正过的13个左输出轴转矩时域的数据样本在LMS TecWare中进行峰值计数，典型结果（021号样本）如图2所示。

图2 021号样本数据峰值计数结果

由图2可知，极大值点（虚线）的分布比极小值点（实线）的分布在绝对数值上明显偏大，因此，只需按照极大值点的统计分布来指定和获得具有一定置信度的最大值即可。

2 参数估计

将试验获得的全部6名驾驶员的样本数据峰值计数结果汇总，得到一个极大值点分布的大样本数据，其中左、右输出轴的数据结果分别如图3和图4中的蓝色柱状图所示。

假设左、右输出轴转矩极大值服从正态分布，则通过极大似然法获得左输出轴转矩极大值的平均值为1 313 Nm、标准差为1 662 Nm，可得图3中黑色的正态分布拟合线；右输出轴转矩极大值的平均值为1 369 Nm、标准差为1 688 Nm，可得出图4中黑色的正态分布拟合线。

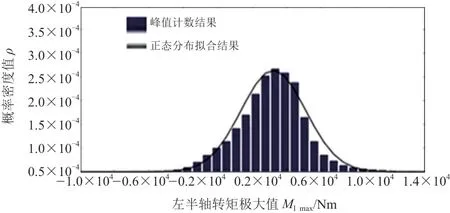
图3 全部数据样本获得的左输出轴极大值分布结果的正态分布拟合结果

图4 全部数据样本获得的右输出轴极大值分布结果的正态分布拟合结果

对照图3和图4，全部数据样本获得的左、右输出轴极大值分布结果的正态分布拟合状况有稍许的差异，造成这种差异的主要原因是试验用车的左、右传动轴结构非完全对称，以及数据采集过程中出现上、下坡转向。

3 由极大值分布获得最大值分布

经统计全部样本数据获得了极大值的正态分布，然后由极大值分布获得最大值分布，并在此基础上最终给出设计谱。

设X1,X2, …,Xn独立同分布于分布函数f(x)和密度函数f(x)，记Y= max (X1,X2, …Xn)，则Y有概率密度函数nFn-1(x)f(x)[7]。对于一维随机变量，最大值Y有概率密度函数F0(x)f(x)=f(x)，对于一维随机变量来说，最大值与极大值同分布，即左转矩最大值服从N[1 313 Nm，（1 662 Nm）2]的正态分布；右转矩最大值服从N[1 369 Nm，（1 688 Nm）2]的正态分布。

既然左转矩最大值服从N[1 313 Nm，（1 688Nm）2]的正态分布，那么可以根据正态分布表，给出具有一定置信度的极大值置信区间上界作为设计谱。比如说，如果指定置信度为99.999%，则设计谱为2 996 Nm，其统计学意义是：在实际使用环境中，左输出轴承受的最大转矩值大于2 996 Nm的概率仅为（1-99.999%），即百万分之一。对于右转矩来说，对应的数值为3 158 Nm。

4 车辆起伏路面行驶时的雨流谱和阶次谱

针对传动轴制定台架试验方案，需采用雨流循环测试方法，以试验对象件（传动轴）所经受的真实损伤（而不是伪损伤）为依据，将真实损伤“搬”到台架上。该技术首先对传动轴所承受的随机转矩时域数据进行雨流计数，得到载荷谱后，再以损伤等价为基础编辑得出阶次谱。

4.1 雨流谱

针对试验处理后的数据分别生成与它们对应的雨流谱，从6名驾驶员中选出具有代表性的驾驶员A，其全部数据生成的左、右传动轴雨流谱如图5所示；通过驾驶员A全部数据生成的左、右传动轴雨流谱图形对照可知，所采集数据的可信度较高。

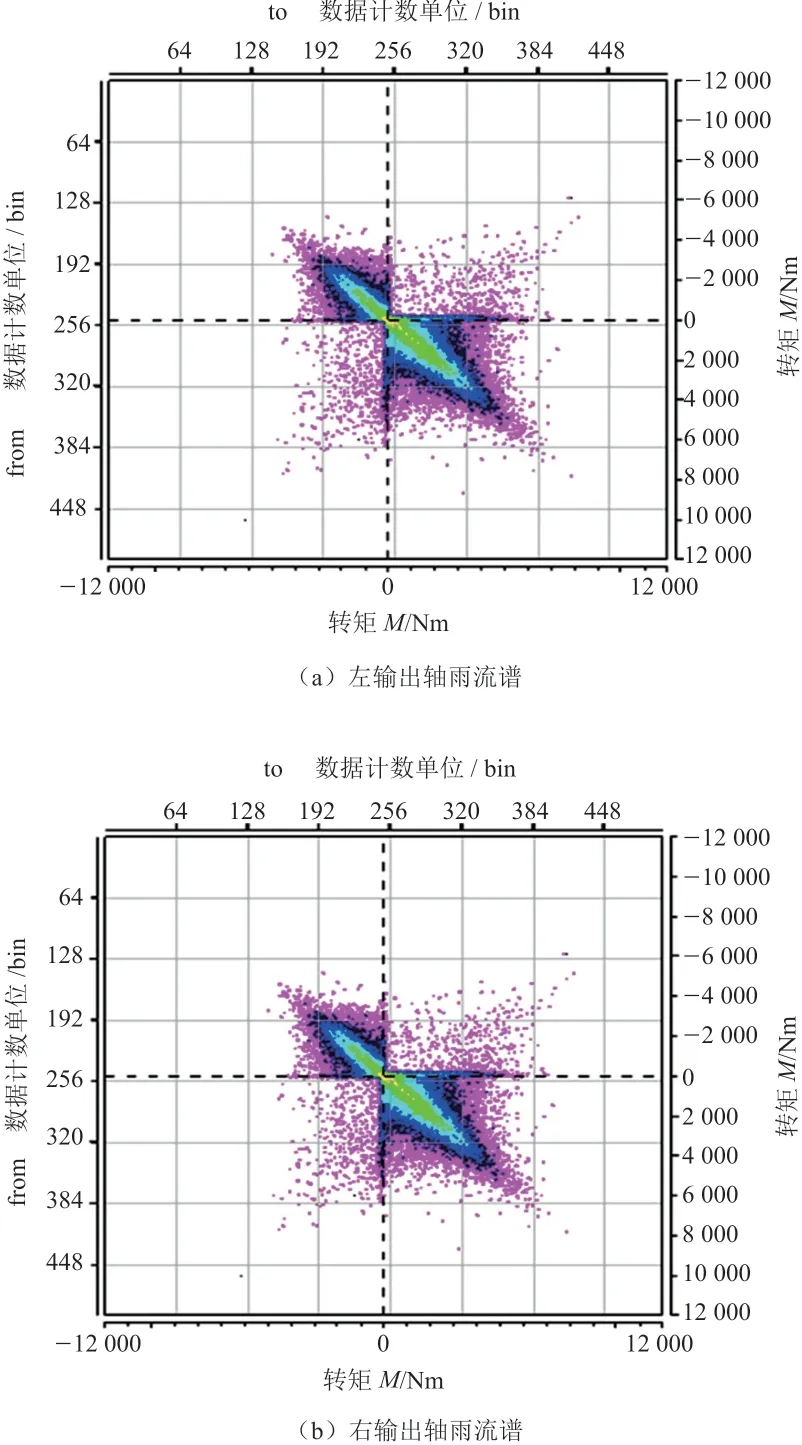
图5 驾驶员A的雨流谱

4.2 阶次谱

在阶次谱编辑过程中，需要结合传动轴材料的真实S-N曲线（本研究中b=5，疲劳极限为1 000 MPa，对应107循环），在考虑平均剪应力的影响（图6）情况下，采用Lsegment平均剪应力修正模型，取系数为0.300，计算真实损伤；将雨流计数矩阵中的每个载荷进行等效损伤平均应力转换，使其成为对称载荷循环，即将均幅值二维载荷谱转换成以幅值为变量的一维载荷谱，然后再次运用等损伤方法将一维载荷谱的幅值转换成8级谱，并针对这8个等级载荷所造成的真实损伤，计算在试验台架上不同载荷幅值等级和频次的载荷旋转次数，从而完成试验方案的初步制定。其主要思路如图7所示。

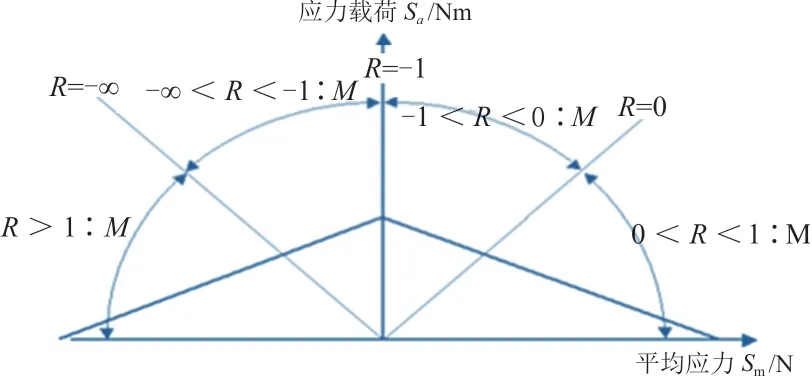
图6 局部平均剪应力修正模型图

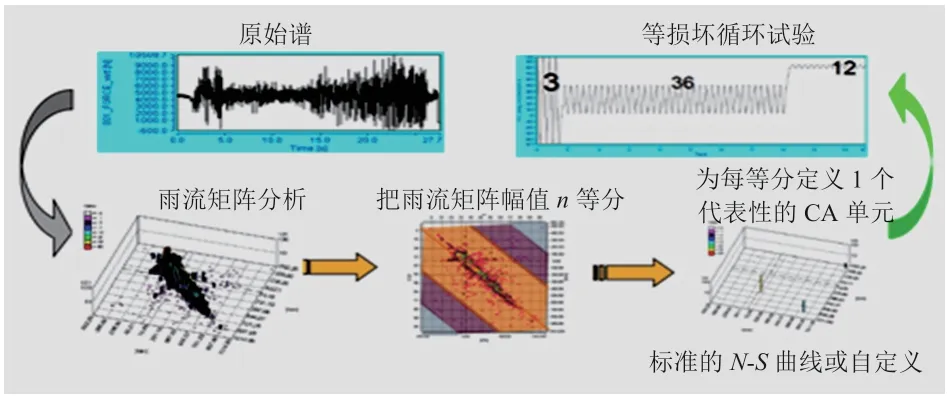
图7 雨流循环测试方法

用不等间隔及等效方法将一维载荷谱转换为8级程序谱，即采用等损伤方法，将幅值在1级与2级之间的载荷循环，分别转换成对称幅值为1级和2级的载荷循环，将幅值在2级与3级之间的载荷循环，分别转换成对称幅值为2级和3级的载荷循环，然后依此类推，将全部数据的对称载荷循环转换为8个幅值级别的对称载荷循环[8]。等效损伤转换公式为：

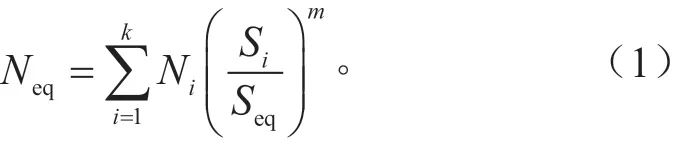
式中：Seq和Neq分别为等效载荷循环的幅值和频次；Si和Ni分别为原载荷循环的幅值和频次；m为S-N曲线的幂指数。把小幅值高频次载荷循环转换成大幅值低频次的载荷循环，对载荷谱疲劳试验起到加速作用。基于雨流循环测试方法制定的左输出轴8级阶次谱见表1。

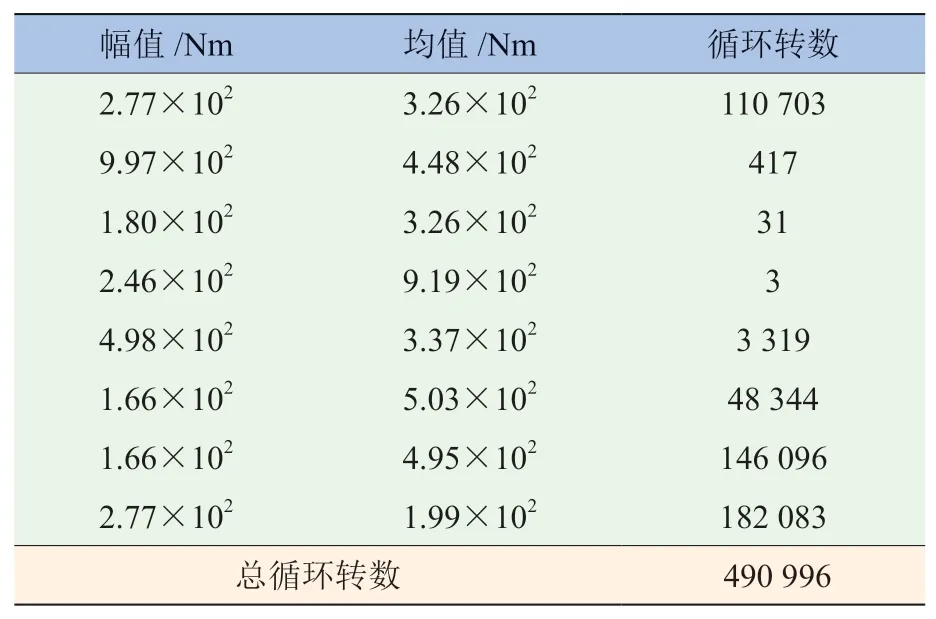
表1 基于雨流循环测试方法制定的左输出轴8级阶次谱

5 损伤数

假设用于制造相关齿轮材料的S-N曲线（循环载荷比R=0）为N·Sb=C（式中，N为循环转，S为载荷幅值，b为材料参数），则齿轮在随机载荷作用下疲劳危险部位所受到的损伤D为[9]：

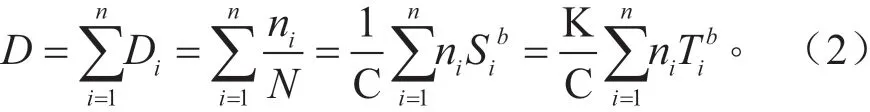
式中：假定齿根疲劳危险点应力水平S与轴转矩T之间呈线性关系，S=KT（K为常数）；ni为对应于轴转矩数值为Ti的旋转频数（也就是齿所遭受的交变转矩在水平为Ti的次数）。

由式（1）可知，由于C与K都为常数，所以对齿根疲劳危险部位造成真正损伤的载荷量值为该数值被称为“损伤数”。在制定台架试验方案时，需将具有统计代表性和满足设计目标的损伤数“搬”到台架上，以完成相关的考核验证。要实现这一目标只需确定材料参数b即可完成。

6 旋转直方图技术

为了计算损伤数（图8），需要6个前进挡和1个倒挡的转速与转矩信息。同时，需要把转矩分割为足够小的bin区间，通过把落入相应bin区间内的转速进行时间积分，在恒定水平的转矩Ti作用下，可得与转矩水平相应的齿轮旋转速度ni，从而得到足够多的用于计算损伤精确的（ni，Ti）数据对[10]。上述过程集成在“旋转直方图”中，其相关技术是制定稳态旋转台架试验方案的关键。

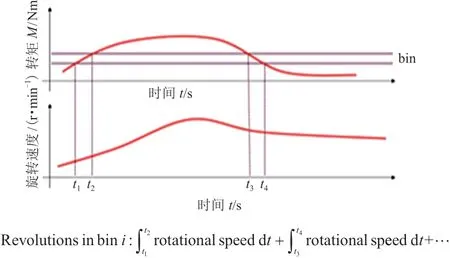
图8 旋转直方图技术原理

分别把全部样本数据分解到6个前进挡和倒挡R的载荷（主要指转矩和转速）进行旋转直方图统计，并作为制定台架试验载荷谱的关键基础数据。在此过程中将产生大量的重要过程数据和图标，是制定面向传动齿轮系统试验谱的核心基础数据。

7 试验载荷谱的制定

试验载荷谱制定的总体思路如图9所示。采集到的数据来自于6名驾驶员的不同样本。首先把每个驾驶员的数据样本放大到相应的总设计里程。在涵盖98%驾驶员的驾驶习惯下，分解到6个前进挡和倒挡R的相应挡位的设计里程为10 000 km。在起伏路面以5挡行驶时从6名驾驶员的数据中选出3个有代表性的数据，将相应的旋转直方图计数结果进行相应比例的放大，其结果见表2。

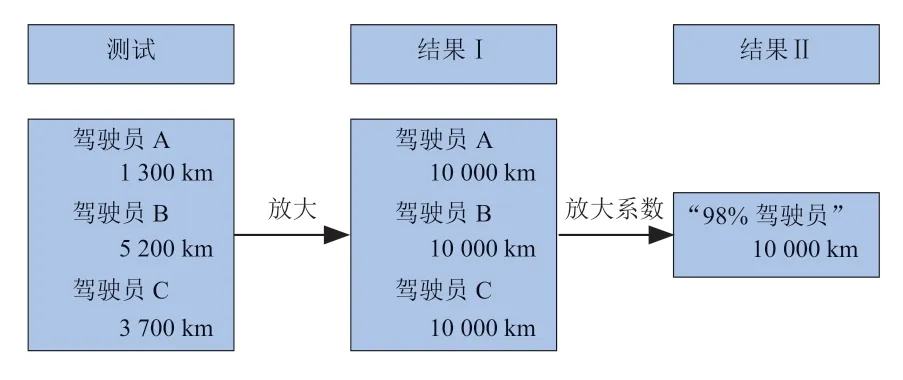
图9 台架试验方案的制定思路

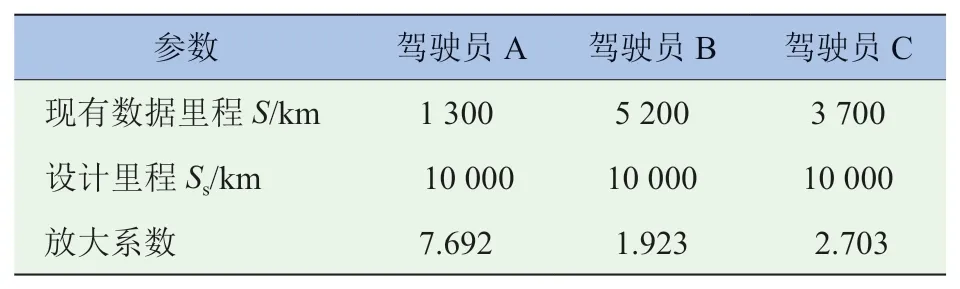
表2 三名驾驶员5挡行驶的放大结果

在此基础上，需要考虑到驾驶员的驾驶习惯，给出带有分位数的外推结果。然而，由于样本数比较小，只有6名有效驾驶员（N=6），所以采用一种特殊的统计方法，以98%的精度来计算驾驶员的特性。先对6名驾驶员在各自区间内的总转数进行平均，其值为再确保转数分布置信水平在98%以上。参照1973年Lipson的研究[11]，利用式（3）计算置信水平为98%的用户转数分布x98%。

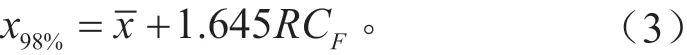
式中：R为转矩区间最大转数与最小转数之间的差值；它的标准差系数参照表3所示，在本试验过程中Cf的标准差系数为0.812；1.645为置信水平为98%时标准正态分布中的值，若需提高置信水平或其它置信度，可参照相应的统计公式进行更改，本文中这一数值全部取为98%。

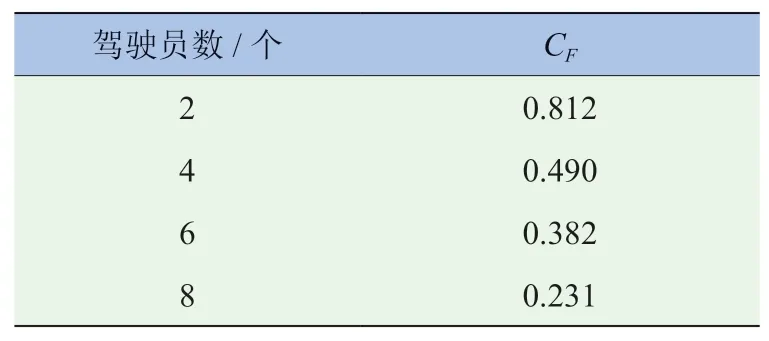
表3 一个区间的标准差系数

下文以履带装甲车辆常用的5挡位行驶为例，进行行驶试验谱的制定，分析其试验谱制定过程，其分析过程对于其它挡位也相同。

涵盖98%驾驶员驾驶习惯的、分解到以5挡位行驶的设计里程为6 738 km，将相应的旋转直方图计数结果进行相应比例的放大，其结果见表4。

表4 以5挡位行驶的放大倍数结果

考虑到驾驶员的驾驶习惯，获得置信水平为98%，总设计里程为10 000 km且保持5挡行驶的T-n结果（转矩-循环数）。在此基础上，采用相等的损伤数来制定台架试验计划即可。在5挡位行驶工况下，齿轮材料的S-N曲线b=5，则如上所述，损伤数为[12]：

为了给试验谱选择合适的转矩，如图10所示，通过旋转直方图计数给出了部分代表性样本数据的总累积损伤分布图。由图可知，以5挡位行驶时载荷比较平稳，因此，在1 400 Nm转矩水平上进行台架试验（表5），在此基础上，在损伤数等效的约束下，确定转矩为1 400 Nm时需要旋转5 164 904转。

表5 以5挡位行驶时设计总里程的试验结果

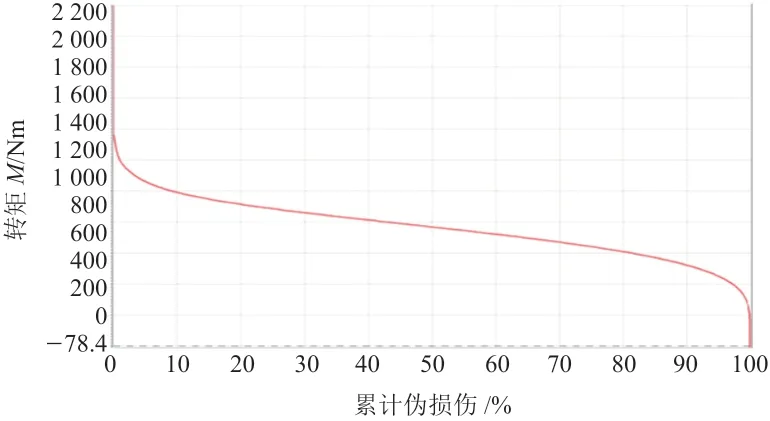
图10 部分样本数据的总累积损伤直方图

当部分代表性样本以5挡位行驶时，对相应的发动机转速数据进行幅值概率密度分布分析，如图11所示，得到发动机转速的幅值概率密度分布结果。由图可知，以5挡位行驶时发动机转速最有可能出现在1 800 r/min，以此确定在转矩为1 400 Nm时，应以1 800 r/min的发动机转速将试验持续47 h 50 min。

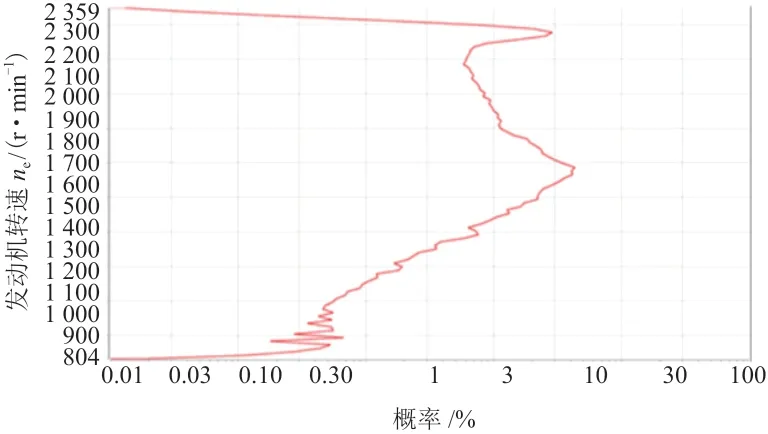
图11 以5挡位行驶时发动机转速幅值概率密度分布

8 稳态旋转台架试验方案

经过上述数据处理，最终可得针对传动轴的稳态旋转台架试验方案，见表6。该方案对应履带装甲车辆在起伏路面上行驶10 000 km时的设计里程。

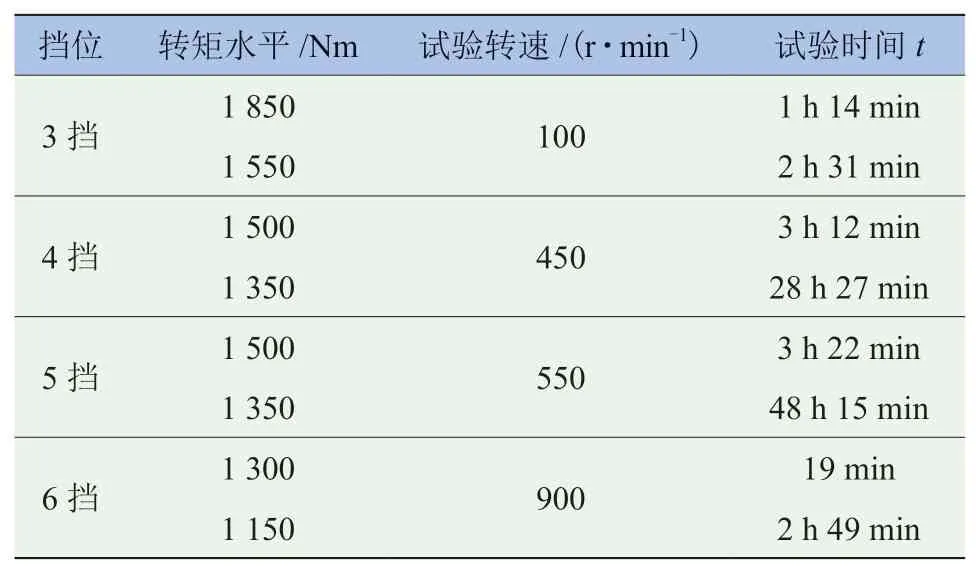
表6 综合传动轴稳态旋转台架试验方案

9 生成具有指定置信度的设计谱

经证明可知，左输出轴转矩极大值服从N[1 161.562 Nm，（4 620.004 Nm）2]的正态分布，那么，根据正态分布表可以得出具有一定置信度的极大值置信区间上界值，作为设计谱安全设计限值，图12所示为13个数据样本获得的左输出轴极大值分布结果及正态分布拟合结果，由图可知设计谱的可靠性较高。

利用统计学正态分布及F检验原理，在实际使用环境中，左输出轴承受的转矩极大值大于2 294 Nm的概率仅为（1-99.999%），即百万分之一。如果指定置信度为99.999%，则设计谱为2 294 N，从而证明了设计谱的可靠性。

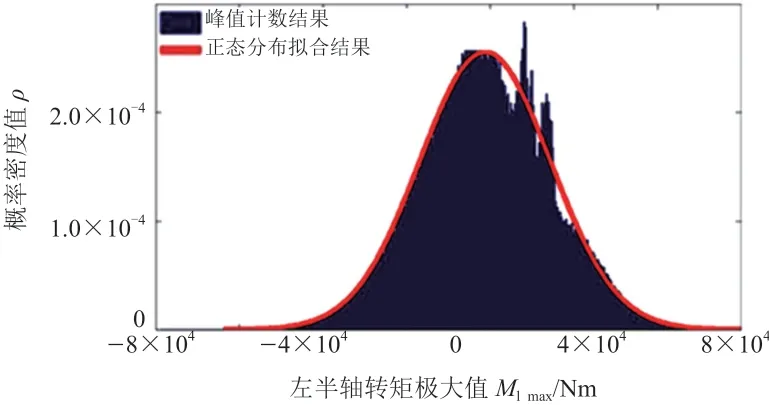
图12 13个数据样本获得的左输出轴极大值分布结果及正态分布拟合结果

10 结论

本研究针对起伏路面行驶时采集后去毛刺和偏置纠正数据样本（主要为传动轴转矩和车速时域数据），制定了传动轴的转矩试验载荷谱，采用雨流循环测试方法，结合传动轴材料的真实S-N曲线，分析了车辆在起伏路面行驶时的载荷谱和阶次谱，以及综合传动系统的试验谱。根据不同幅度的载荷所造成的损伤形成了8级谱，并针对这8个等级的载荷所造成的真实损伤，计算在试验台架上所需要重复的转数，将转速、转矩和车速信息按照履带装甲车辆行驶挡位进行分割，对于每个行驶挡位制定稳态旋转台架试验方案。在分析过程中，将车辆的总设计历程和轴转矩载荷的不确定性纳入考量，并将挡位分割及统计各挡位数据里程，以此形成试验载荷谱的制定方法，最后形成稳态旋转台架试验方案。

按照峰值计数方法的极大值点的统计分布来获得具有一定置信度的最大值，参照极大值分布函数推导出最大值分布，并在此基础上最终给出设计谱。该编谱技术为履带装甲车辆传动轴疲劳设计提供部分参考，并推广应用于工程或民用车辆传动件的抗疲劳设计中，具有一定的实用价值。