基于多目标遗传算法优化和研究CIASI保险指数安全性能

潘志红，宋晋华，陆劲昆，胡 浩，施志平，陈虹吉，李忠超，胡 楷

（东风汽车有限公司 东风日产乘用车公司技术中心，广州 510800）

《中国统计年鉴2018》显示，2017年中国共发生203 049起交通事故，死亡63 772人，受伤209 654人，直接财产损失12.1亿元，数据显示目前我国的交通安全问题仍然很严峻[1]。2017年，中国颁布了中国保险汽车安全指数规程（简称C-IASI）[2]，规定了正面25%重叠碰撞、侧碰和车顶抗压等评价项目，相比国标和2018版本C-CNAP[3]，C-IASI对车体耐撞性的要求更高。此外，随着能源和环境问题的突出，以及CAFC法规的加严，轻量化成为各个汽车生产厂商关注的重点。大量研究表明，汽车质量每减少10%，燃油消耗可降低6%～8%，尾气排放将减少5%～6%[4]。因此，在对应新安全标准提高车辆耐撞性的同时，也需要考虑车辆的轻量化。

关于轻量化，不少学者进行了相关的研究。胡红舟等[5]提出了一种铝合金波纹板加强结构设计方案，用来加强盒形汽车防撞梁。刘昌业等[6]探讨了提升微型客车翻滚耐撞性和轻量化的多目标优化方法。张君媛等[7]描述了B柱碳纤维加强板的设计和优化方法，对纤维复合材料的铺层厚度、角度和铺层进行顺序优化。吕晓江等[8]基于正面40%重叠可变形壁障碰撞对骡子车进行了可靠性优化。以上文献更多的是基于单项碰撞的耐撞性研究，考虑到在整车碰撞性能开发过程中，不同的碰撞性能之间关联的结构件有共通的部分，因此，有必要综合考虑整车各项碰撞性能并进行整体优化。本文以正面25%重叠碰撞、侧面碰撞和车顶抗压3项安全性能为例，利用DOE试验设计、Kriging代理模型和多目标可靠性优化，对乘员舱关联结构件厚度进行优化设计，最终在满足性能目标的前提下，实现轻量化。

1 优化方法

1.1 确定性和可靠性优化

多目标确定性优化问题数学模型可以描述为[9]：

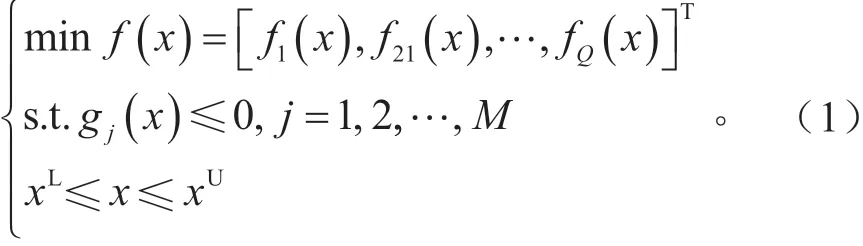
式中：f(x)为目标函数；gj(x)为约束函数；Q和M为目标函数和约束函数的数量；xL和xU为设变变量x的上下限。工程设计中，设计变量往往存在波动和不确定性[10]，相比确定性优化，可靠性优化可以减小响应的波动，使确定性优化解远离约束条件边界，降低响应在设计点上的敏感度[11]。基于可靠性优化的数学模型可以描述为：

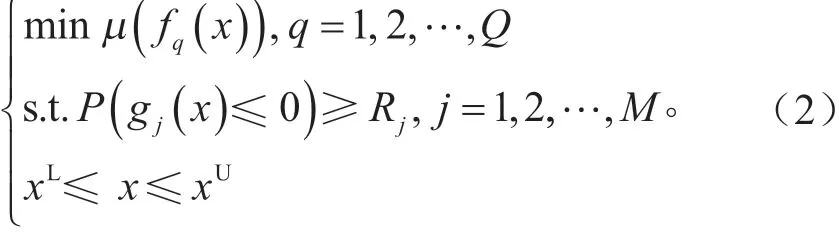
式中：μ为目标函数均值；P(gj(x)≤0)为满足第j个约束的概率；Rj为约束函数的期望可靠度[11]。

1.2 轻量化设计路线

基于径向基RBF代理模型的车身结构多目标可靠性优化设计流程如图1所示[9]，主要有以下几个步骤：

（1）从节省计算成本考虑，将正面25%重叠碰撞、侧面碰撞和车顶抗压3项安全性能分别从整车模型中解耦，并构建有限元子模型。

（2）通过应力分析法，选取关键结构件作为设计变量，并利用最优超级拉丁方试验进行试验设计。

（3）构建目标函数和约束条件，并结合有限元软件计算各个样本点的响应值。

（4）基于遗传算法，采用非支配排序遗传算法NSGA-II对Kriging代理模型进行多目标的确定性和可靠性优化。

（5）采用蒙特卡洛模拟技术对优化结果进行可靠度评估，并最终输出优化方案。

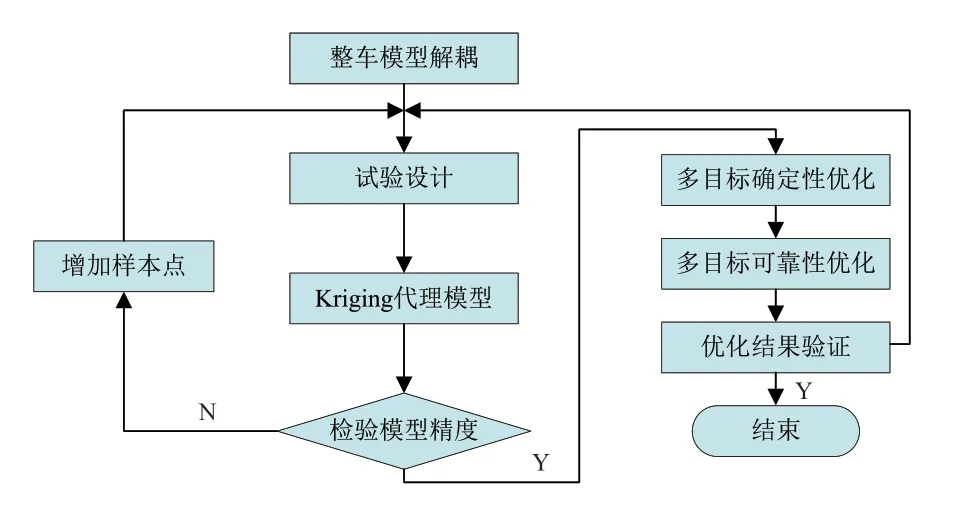
图1 多目标可靠性优化流程

2 车辆安全和轻量化开发

新车型开发采用成熟平台共线生产，能够有效缩短开发周期，降低开发成本，是目前国内外主机厂缩短新车型开发周期最有效的方法，国外欧美和日系主流汽车厂商已具备较齐全的平台系列，国内汽车厂商也在逐步加快平台化建设[12]。本文基于现有平台，仅对乘员舱主要结构件进行优化设计。

2.1 整车模型解耦

根据文献[13]所述，在结构件单独从整车上取下来和保留在整车上这两种情况下，部件的碰撞特性并不相同，但二者的趋势仍是一致的。为了提高计算效率，本文分别对保险指数的3项安全性能正面25%偏置碰撞、侧面碰撞和车顶抗压进行有限元子模型解耦。

首先，对于正面25%偏置碰撞，在整车碰撞过程中，与乘员舱接触的是车辆轮胎、轮毂或者壁障，车辆轮胎、轮毂或者壁障与车辆的相互接触力超过了乘员舱结构所能承受的最大耐力时，乘员舱中的结构件容易出现图2所示的溃缩和变形，主要表现为A柱和前立柱折弯及门槛的压溃变形。从车辆轮胎、轮毂或者壁障与车辆的相互接触力与乘员舱能承受最大耐力的关系出发，车辆轮胎、轮毂或者壁障与车辆的相互接触力低于乘员舱最大耐力时，乘员舱在25%偏置碰撞工况下变形小或者不变形，而当车辆轮胎、轮毂或者壁障与车辆的相互接触力大于乘员舱所能承受的最大反力时，乘员舱容易变形或者变形较大。因此，构建了如图3所示的局部模型，并以局部模型的刚性轮胎与乘员舱之间的相互接触力F1(x)作为优化目标，其中轮胎面设定为刚性面，匀速沿车身纵向挤压乘员舱，乘员舱结构包含A柱、前防火墙结构、前立柱、B柱、门槛、顶盖侧梁、顶盖、前挡风玻璃和底板平台结构件。

图2 正面25%偏置碰乘员舱压溃变形

图3 正面25%重叠碰撞解耦模型

图4a为刚性轮胎与乘员舱的相互作用力，图4b为乘员舱在相互作用力处于波峰时刻的变形模式，相互作用力处于波峰值时，门槛外板出现失稳折弯，说明了门槛对于正面25%偏置碰撞的重要性，门槛的变形模式属于常见的轴向压溃，与图2的试验结果类似。

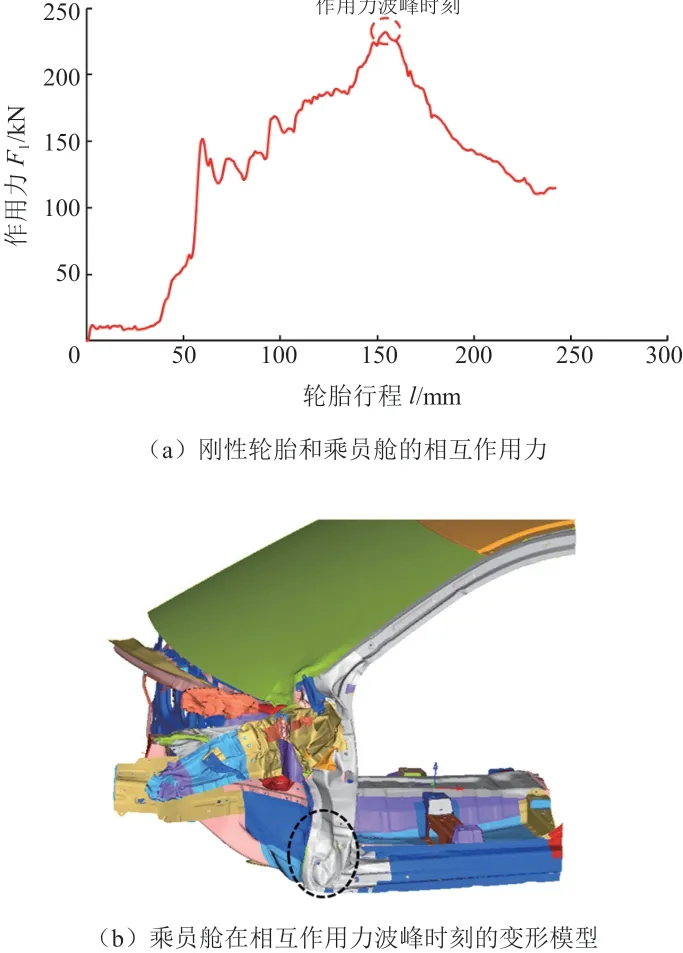
图4 正面25%重叠碰撞强度和变形模式

其次，对于侧面碰撞，与正面25%偏置碰撞共用局部简化模型，只是壁障和施力工况做差异化设计，如图5所示。设置侧碰壁障匀速沿着车身横向挤压乘员舱，根据保险指数侧面碰撞评价规则要求[14]，对碰撞后B柱与驾驶员座椅中线之间的距离进行分级评定，当B柱与驾驶员座椅中线之间的距离≥12.5 cm时，评价侧碰车体结构为优秀；当距离在5.0～12.4 cm之间时，评价车体结构为良好；当距离在0～4.9 cm之间时，评价车体结构为一般；而当距离小于0时，则评定侧碰车体结构为差。由于本文所研究的车辆安全目标为车体结构侧碰优秀，即B柱与座椅中线之间的距离需≥12.5 cm，当B柱与座椅中线之间的距离为12.5 cm时，壁障横向行程预计为300 mm左右，所以本文以壁障在300 mm行程内壁障与乘员舱的最大相互接触力F2(x)作为优化目标。变形模式跟实际试验结果类似，即B柱下端压溃形成塑性铰，门槛外板向车内翻。

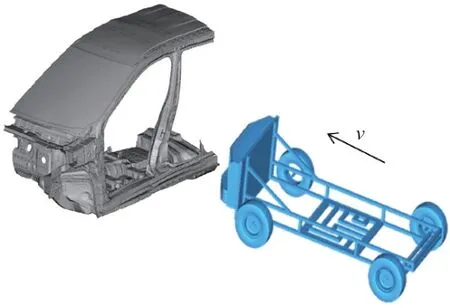
图5 侧面碰撞解耦模型

最后是车顶抗压性能，如图6所示，参考文献[2]中保险指数章程关于车顶抗压试验的要求，设置压板使其纵轴前倾角为水平向下 5°±0.5°（侧视），横轴外倾角为水平向下25°±0.5°（前视），并以5 mm/s施加载荷直至加载位置≥127 mm，提取压板和乘员舱在127 mm行程内的相互作用力F3(x)作为优化目标，出于计算速度考虑，车顶抗压局部简化模型和正面25%偏置碰撞和侧面碰撞共用，只是约束和施力工况不同，并且暂未考虑侧门总成的影响，优化的方向是优化后的结果不低于初始值。

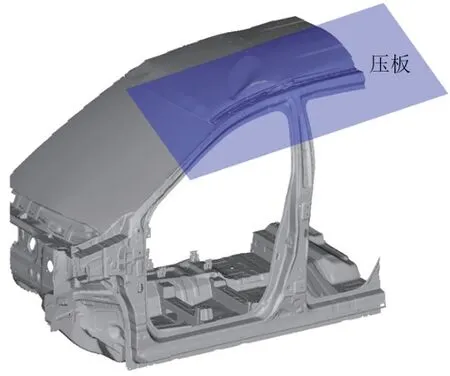
图6 车顶抗压解耦模型

2.2 多目标优化

所研究的优化目标为解耦模型和壁障的相互作用力与各个设计变量的质量和，其中解耦模型和壁障的相互作用力评价包含正面25%偏置碰撞、侧面碰撞和车顶抗压3个工况，该优化课题属于常见的多目标优化。由于板件强度跟成型工艺关联较大，甚至会影响到主机厂对供应商的选择，因此，本研究在钣金材料牌号和强度不变的前提下，只对板件的厚度进行优化。

2.2.1 设计变量

根据正面25%偏置碰撞、侧面碰撞和车顶抗压3个工况的传力路径和应力，在考虑平台不变的情况下，选取x1-侧边梁外板、x2-A柱外板、x3-前立柱外板、x4-门槛外板、x5-B柱外板、x6-侧边梁内板、x7-A柱内板、x8-前立柱内板、x9-门槛内板、x10-B柱内板和x11-顶盖中横梁11个变量作为优化对象，如图7所示。考虑现有钢板的可选厚度范围和加工制造的不确定性，假设设计变量服从正态分布，通过实际统计核算，所用宝钢钢板厚度标准差σ为0.011，设计变量见表1。

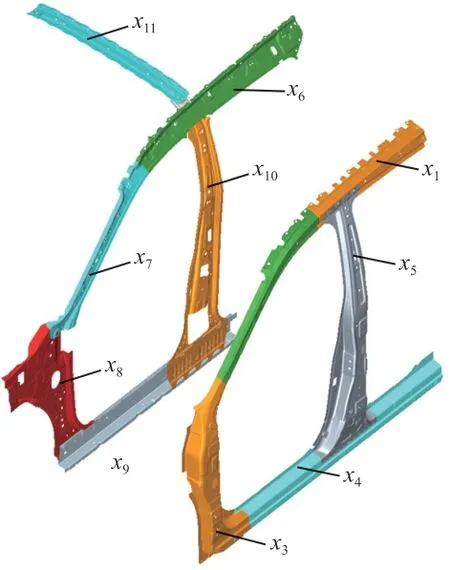
图7 设计变量示意图

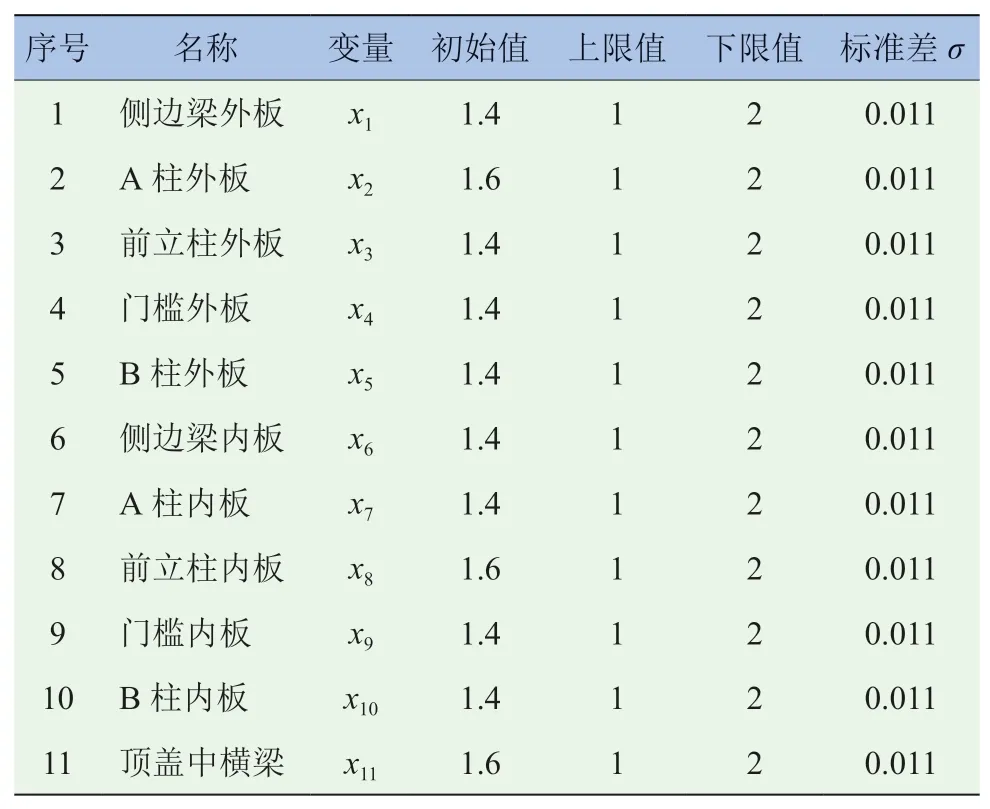
表1 设计变量定义

2.2.2 优化目标和约束条件

从耐撞性的角度考虑，为了对耐撞性强度进行整体的优化，根据实际工程中3项性能提升的难易程度，通过分配权重比得到综合强度F(x)，如2.1节中整车模型解耦所述，F1(x)为正面25%偏置碰撞刚性轮胎在300 mm行程内和乘员舱的最大相互作用力，F2(x)为侧面碰撞壁障在300 mm行程内壁障与乘员舱的最大相互接触力，F3(x)为车顶抗压压板和乘员舱在127 mm内的最大相互作用力。

由于本文的研究目的是提高CIASI的安全性能并控制质量增加，所以设定3项性能分别不低于初始值，各个变形质量和波动范围在5%以内。

2.2.3 建立Kriging模型及讨论

理论上构建Kriging近似模型需要的样本数至少为2n+1[8]，其中n代表变更个数，即至少需要23组，考虑要近似模型的精度和解耦模型的计算效率，通过最优超拉丁方法进行41次试验，并利用有限元软件LS-DYNA计算各样本的响应值。表2为设计样本和仿真结果统计。

基于表2的统计数据构建Kriging代理模型，并进行精度分析，重新计算5组样本，对比近似模型和CAE仿真结果数值，得到表3所示的误差分析结果，从工程的角度考虑，精度已经足够，可用于后续的优化分析。

表2 最优超级拉丁方抽样

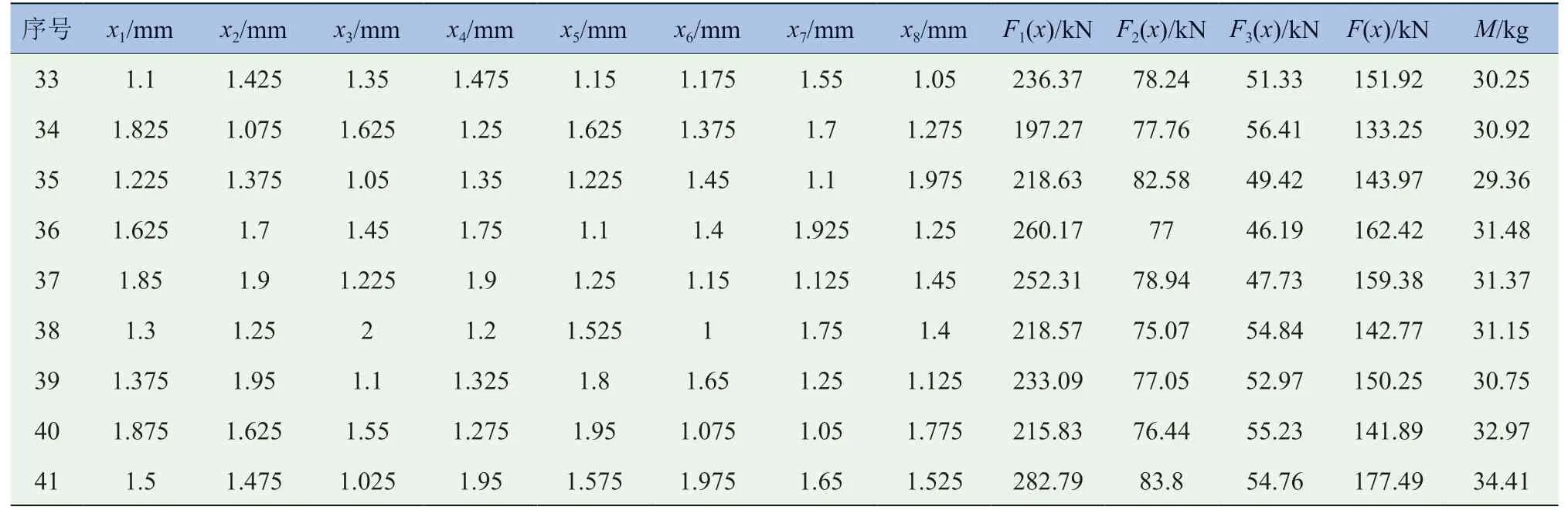
续表2：

表3 代理模型误差分析

图8列出了各设计变量对响应的贡献率，对于正面25%偏置碰撞工况，影响度较大的是x4-门槛外板、x2-A柱外板、x9-门槛内板、x3-前立柱外板、x8-前立柱内板和x1-侧边梁外板，这6个最灵敏的结构件构成图9a所示的传力路径。当壁障或者前轮轮胎轮毂撞击乘员舱时，最新撞击到x3-前立柱外板和x8-前立柱内板构成的前端结构，接着将力通过路径①传递到路径②和路径③。对于侧面碰撞工况，影响度较大的是x5-B柱外板、x4-门槛外板、x9-门槛内板、x10-B柱内板、x11-顶盖中横梁和x1-侧边梁外板，这6个最灵敏结构件构成图9b所示的传力路径④～⑥。当壁障撞击x5-B柱外板和x4-门槛外板后，将力传递给平台的座椅横梁、侧边梁传力路径⑦与顶盖中横梁传力路径⑥及顶盖前后横梁等，其中路径⑥提供车辆横向力的支撑。对于车顶抗压工况，影响度较大的是x5-B柱外板、x10-B柱内板、x2-A柱外板、x11-顶盖中横梁、x7-A柱内板和x3-前立柱外板，6个结构件构成图9c所示的传力路径⑧～⑩，试验时压板将力施加到顶盖侧梁，顶盖侧梁通过路径⑨和⑩传递向下的力，并通过路径⑧传递车辆横向力。

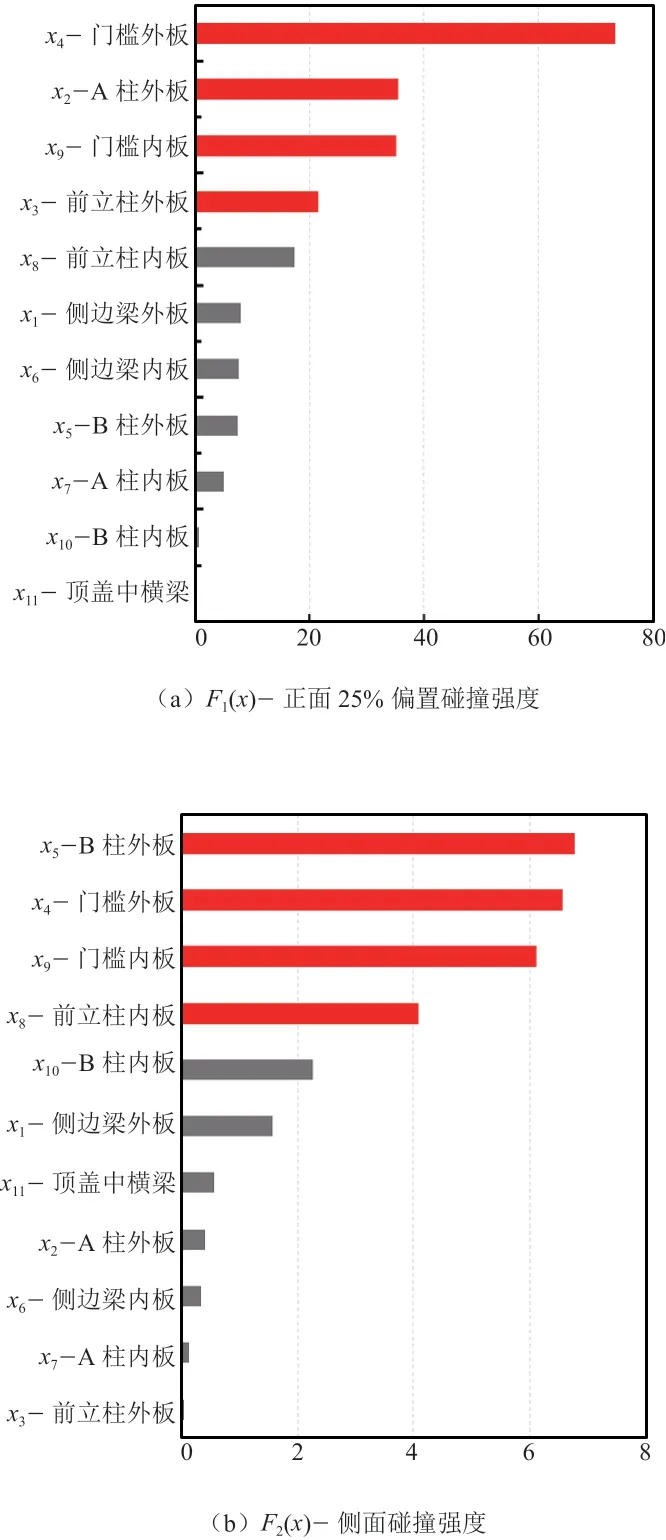
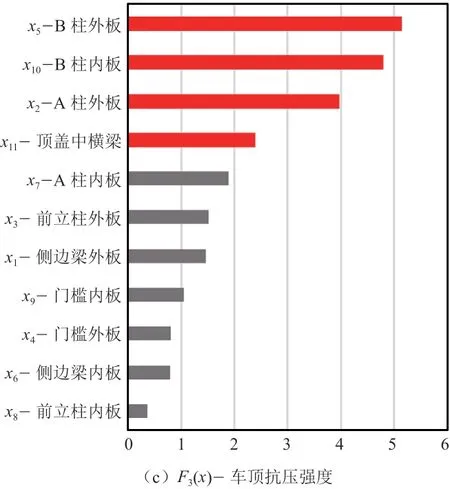
图8 设计变量对各个工况的贡献度

图9 各个工况的灵敏结构件及传力路径

2.2.4 优化结果及讨论

该多目标确定性优化简化模型为：

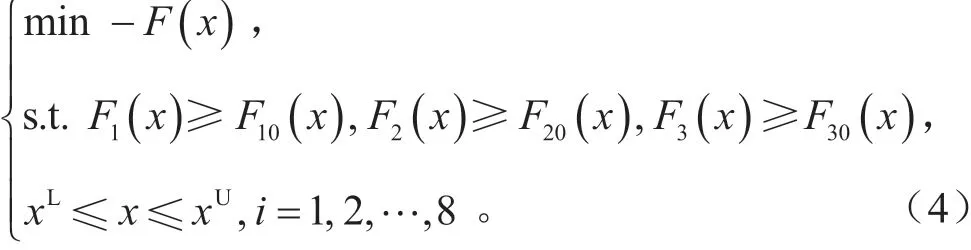
式中：F(x)为式（1）的综合强度；M(x)为变量x1～x11的质量和；F10(x)、F20(x)、F30(x)为设计变量初始值时对应正面25%偏置碰撞、侧面碰撞和车顶抗压的强度；xL和xU为设计变量的上下限，即约束3项子性能不能低于初始值。利用非支配排序遗传算法NSGA-II对综合强度F(x)进行有无约束的确定性优化，得到有无约束的确定性优化Pareto前沿，如图10所示。由图可知，当约束3项子性能不低于初始值时，对应的Pareto前沿范围减小。

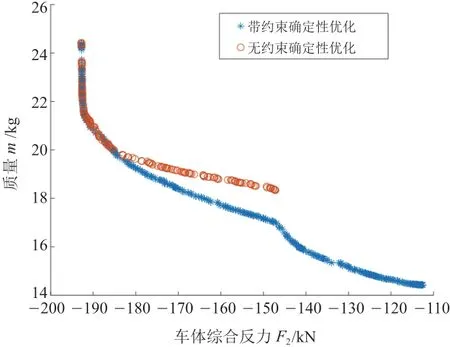
图10 有无约束的确定性优化Pareto前沿

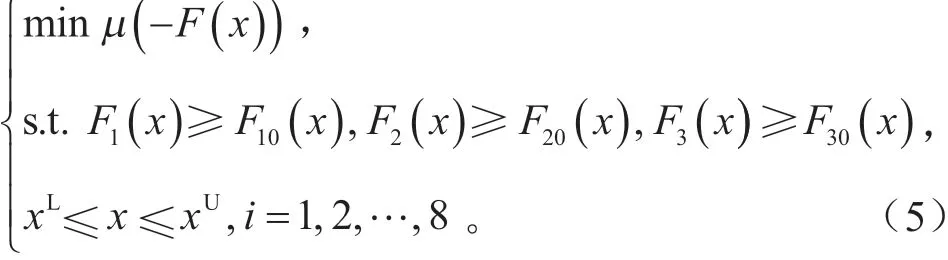
该可靠性多目标优化简化模型为：

本文分别求解95%和99%的可靠度，利用非支配排序遗传算法NSGA-II对F(x)进行确定性和可靠性优化设计，得到图11所示的Pareto前沿，并选取了表4所示的确定性优化和可靠性优化解集。

由图11和表4可知，确定性优化、95%可靠度和99%可靠度对应的设计变量的解比较接近，当M(x)相当时，可靠度越大，F(x)越低，但数值差距较小，可见随着钢板生产的稳定性提高，板厚标准差降低，可靠性优化和确定性优化的差异不大。根据优化的设计变量，考虑量产实际和现有钢板厚度系列，对表4的设计变量进行圆整和修正，并通过CAE重新仿真，得到的结果见表5。

表4 确定性优化和可靠性优化解集

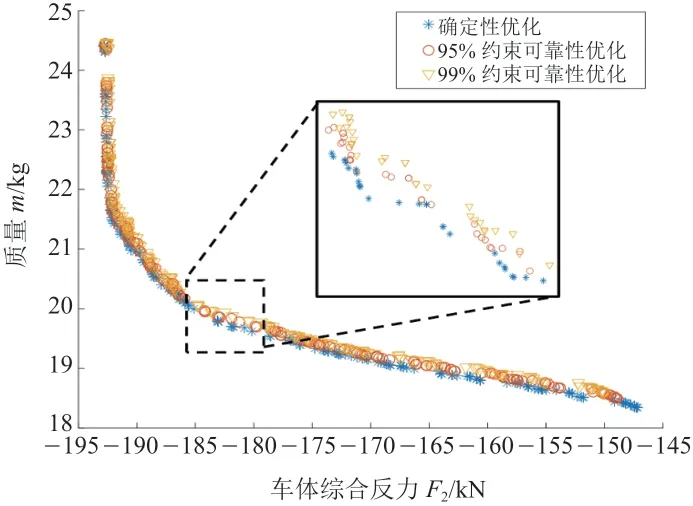
图11 确定性和可靠性优化Pareto

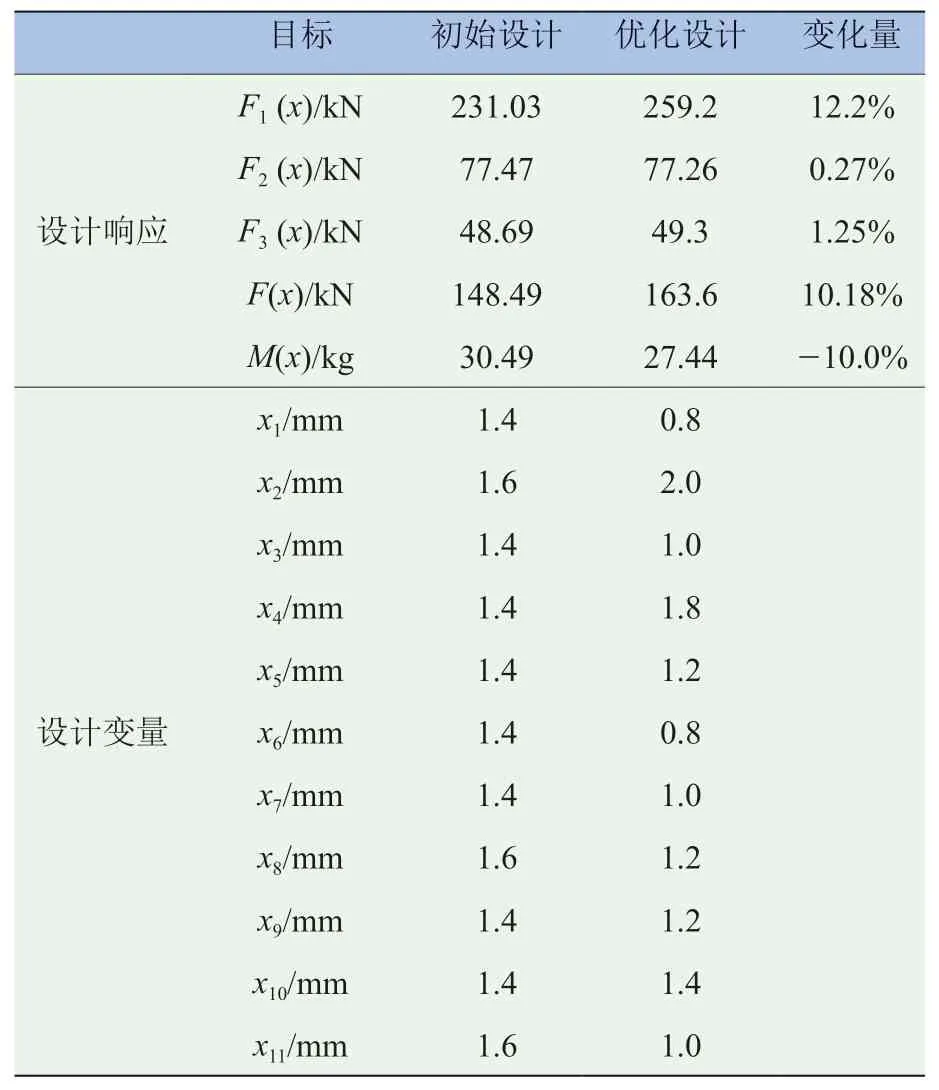
表5 初始设计与优化设计的仿真结果对比

由表4可以，优化后设计变量x1～x11的质量和减少3.05 kg，相比原来轻量化10.0%，正面25%偏置碰撞强度F1(x)提高12.2%，侧面碰撞乘员舱强度F2(x)和车顶抗压强度F3(x)基本维持原来水平，由于25%偏置碰撞强度F1(x)分配的系数0.5高于侧面碰撞乘员舱强度F2(x)和车顶抗压强度F3(x)，所以有明显提升，同时综合强度F(x)也提高10.18%。

2.3 整车验证

分别验证整车级别的正面25%偏置碰撞、侧面碰撞和车顶抗压的强度，车体结构分别获得良好、优秀和优秀的成绩。

3 结论

（1）从提升计算效率的角度考虑，从整车模型上解耦出简易模型，针对正面25%偏置碰撞、侧面碰撞和车顶抗压3项性能，通过同一个简易模型快速计算各个工况乘员舱的耐撞强度。

（2）通过Kriging代理模型研究设计变量对正面25%偏置碰撞、侧面碰撞和车顶抗压3项性能的影响度和传力路径，总结其规律并指导新车开发。

（3）通过确定性多目标优化、可靠性多目标优化，发现随着钢板生产稳定性的提高，板厚标准差降低，可靠性和确定性优化差异不大。

（4）通过多目标遗传算法优化，相比初始设计，优化设计综合强度提高10.18%，同时实现轻量化10.0%，减重3.05 kg。