基于UbD理论的单元教学设计——以平面解析几何为例
2020-10-28葛丽婷施梦媛于国文
葛丽婷,施梦媛,于国文
基于UbD理论的单元教学设计——以平面解析几何为例
葛丽婷1,施梦媛2,于国文3
(1.杭州市杭州中学,浙江 杭州 310002;2.福建省厦门第一中学,福建 厦门 361003;3.北京教育科学研究院 基础教育教学研究中心,北京 100036)
基于UbD的单元教学设计是对当前课程体系的一种温和有序重构.结合大概念、理解六侧面、基本问题、评估与反馈以及WHERETO元素可以进行基于UbD理论的单元教学设计.通过对高中平面解析几何进行基于UbD的设计,旨在为初探高中数学课程如何设计追求理解的大单元教学设计的数学教育者提供参考和借鉴.基于UbD的单元教学具有可操作性,它使课程设计得以整体化和连续化,在培养学生核心素养的同时还能促进教师的专业发展.
UbD理论;单元教学设计;平面解析几何
1 问题提出
2014年《关于全面深化课程改革落实立德树人根本任务的意见》提出了“核心素养”的概念后,“核心素养”已成为近年中国教育研究者及一线教师研究的重要课题.2017年,新版《普通高中数学课程标准(2017年版)》对数学核心素养是什么的问题作出了回答,普通高中新课程标准的出台明确了学科目标从知识点的了解、理解与记忆向学科核心素养的关键能力、必备品格与价值观念的培育转变[1].那么,“如何将数学核心素养落实到课堂中”这一问题便是亟待解决的.
传统课堂中学生对教师传授的知识更多是记忆和模仿,这样的教学有两大问题:其一在于使用记忆获得的记忆型知识易被遗忘,其二在于学生对这样的知识缺乏深入的理解,无法融会贯通,难以将其迁移到现实生活中解决问题[2].《人是如何学习的:大脑、心理、经验及学习》中提到,当学习者知道并理解可以应用于新环境中的问题的基本概念和原则时,知识的迁移最有可能发生.理解学习比简单地记忆更有可能促进交流[3].因此,培养学生的理解力,让学生对所学知识产生深入的理解,能够在一定程度上促进学生在现实生活中进行知识迁移,使得通过学校培养学生的核心素养成为了可能.在这个意义上,追求理解的教学是在课堂中落实核心素养的可操作途径.另一方面,国内崔允漷教授发出了学科核心素养呼唤大单元教学设计的倡议.学科核心素养的出台倒逼着教学设计的变革,指向学科核心素养的大单元设计是学科核心素养落地的关键路径[4].
美国哈佛大学教育研究院的IJTFU项目集6年成果而提出的面向理解的教学设计模式,以“生成性目标—理解性目标—理解性实作—追踪式评价”为教学设计框架[5].为了让学生达到知识的理解目标,该模式将教学分为了4个核心步骤,依次回答了“教什么?”“学生需要什么?”“如何达到学习目标?”“怎样知道学生已掌握这些知识?”等4个问题.追求理解的教学设计在关注教什么和怎么教的同时,还关注学生理解什么以及有什么证据可以证明学生获得了“理解”.基于这样的思考,Grant Wiggins和Jay McTighe针对传统教学设计中“活动导向的教学设计”以及“灌输式学习”的教学设计误区,提出了“追求理解”的教学设计方案(Understanding by Design,下文简称UbD),也称为逆向教学设计,为课堂教学提供新的思路.UbD的设计理念与崔允漷教授提出的大单元设计的6要素不谋而合[4].因此,研究以平面解析几何内容为例,结合UbD理论旨在初探高中数学课程中如何设计追求理解的大单元教学设计.
2 UbD理论概述
2.1 大概念
大概念(big ideas)是学科的核心,具有内在的可迁移特性,将离散的主题和技能联结起来[6].它用于强化思维,连接不同的知识片段,使学生具备应用和迁移的能力.不同于学科知识中需要掌握和完成的重要内容与需要熟悉的知识,大概念所包含的知识范围更大,其概括性、抽象性、普遍性的特点与核心素养的迁移要求可谓无缝对接[7].大概念指向学科结构的中心,与学科核心素养有着潜在的关联,为学科核心素养的落实扮演重要角色[8].UbD理论也提出大概念,并主张围绕“大概念”设定教学目标、基本问题以及预期结果.数学学科中关系和函数、方程和不等式、形状和立体图形、可能性等都可成为单元设计中的大概念.例如,在平面解析几何的单元设计中,曲线与方程就是一个大概念.
2.2 理解六侧面
对所学知识的深度理解是学生得以发展的前提.特别对于身处信息时代的学习者而言,计算机已可以胜任人类大部分知识记忆的工作,对核心问题的理解力、创新力便成了人的核心竞争力的重要体现.因此,追求理解是信息时代学习的核心价值,也是有效学习的关键条件[9].数学核心素养形成的表现也包括对理解能力的评估[10].那么,如何架构“理解”呢?UbD理论认为所谓理解并不是简单的知道和明确,理解是指对知识的一种迁移,包括了对知识和技能的有效应用以及对事物进行有意义地推断,并提出了理解六侧面,如果学生理解了,就能达到[6].
侧面1——能解释:适恰地运用理论和图示说明事件、行为及观点,并有自己的见解.通过归纳或推理,系统合理地解释现象、事实和数据;洞察事物间的联系并提供例证.
侧面2——能阐明:演绎、解说和转述,从而提供某种意义.
侧面3——能应用:在新的、不同的、现实的情境中有效地使用知识.
侧面4——能洞察:批判性的、富有洞见的观点.
侧面5——能神入:感受别人的情感和世界观的能力.
侧面6——能自知:知道自己无知的智慧,知道自己的思维模式与行为方式是如何促进或妨碍了认知.
2.3 基本问题
基于问题学习让学生在问题中获得知识,又会灵活运用知识解决问题,以发展学生的高级思维、培养自主学习和团结合作的能力[11-12],以问题为基础的教学已然是深化改革的一条基本思路,也是培养学生核心素养的有力途径.而UbD理论同样将对问题的架构放在关键地位,提出了“基本问题”的概念.所谓的基本问题是学科知识的核心,包括相关的核心大概念和核心思想,也是学习核心内容必须解决的问题.它使得学生参与到各种各样的高阶思维中以增强学习能力[6],更重要的是能激发学生对更多问题的深度思考,并对已有经验进行反思,让学生主动与先前知识产生有意义的联系进而为知识的迁移创造机会.那什么样的问题是有价值的?如何提出合适的基本问题?如图1的问题过滤器[6]正是一个产生基本问题的有用工具,帮助教师在教学活动的设计中筛选出值得深入探究的有效问题.

图1 问题过滤器
2.4 评估与反馈
基于UbD理论的设计中,教学过程是其中重要的一个方面,而评估也是设计中重要的一环.评估不仅是传统意义上的考试与测评,不能因为考试的结束而终止评估.UbD理论认为需采取连续跟踪式的评估,从简单到复杂、从短期到长期、从非真实情境到真实情境、从高度结构化到非结构化,形成评估的连续系统,如图2所示[6].其中,表现性任务是UbD理论的特色,有研究指出将真实情境的表现性任务与教学结合有利于促进学生关注深层知识的理解[13].所谓表现性任务,是指在一个复制或模拟现实世界的情境中检验知识与能力的任务,是学生获得与真实工作与生活一样的真正“测试”[6].表现性任务使学生可以学到学校之外的现实世界中如何真正运用学校中学到的知识和技能,从而弥补传统评估方法的局限性.不同层次的评价方式适用于不同性质的知识内容,如图3[6],确保评估的高效与准确.

图2 评估的连续系统
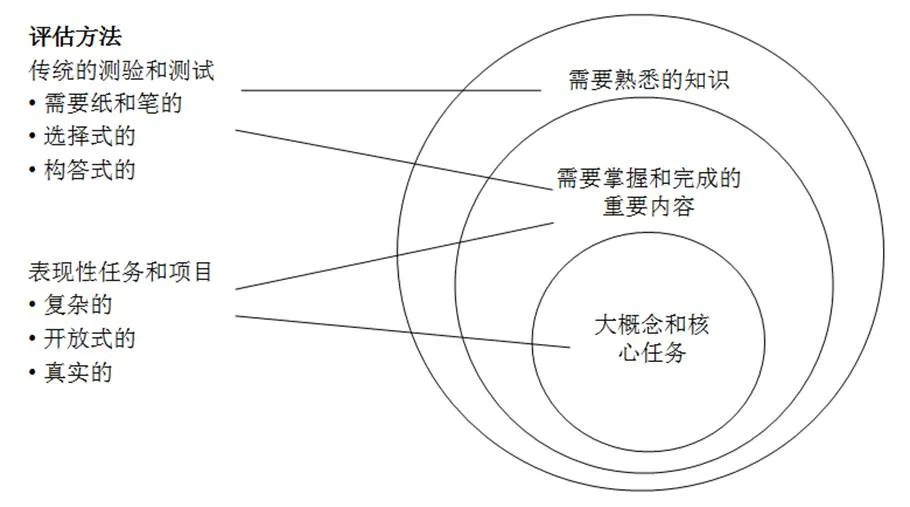
图3 课程重点和评估方法
上述评估适用于教师和学生对他人的评估过程,但正如学者们所倡导的核心素养不是教出来的,而是学生悟出来的,学生个体对自我感悟有准确地衡量,对掌握的任务有自己的认知与看法是发展素养的重要组成部分.而UbD理论也同样重视自评,要求学生能准确地进行自我评估并有效地自我调节,同时教师也能据此了解学生所获理解的复杂程度.要注意的是,在教学过程中,评估者要立即提供评估与反馈.Marzano、Pickering和Pollock的研究也指出,评估后立即提供反馈,有利于提高学习能力;有参考标准的反馈比无参考标准的反馈对学生学习的影响更大[14].教师需对学生的作品和表现提出统一的评估标准,使得学生的表现与其真实的理解层次对应,保证评估的一致性和公平性.
2.5 WHERETO元素
在一个教学设计中,设计学生活动可以有多种方式.为了更好地实现学习计划,引导学生更深入地思考问题,教师可以更全面地考量学生对知识的理解程度,教学过程的设计可以借鉴Grant Wiggins等提出的“WHERETO”元素[6],各元素的含义如表1所示,其有助于帮助设计者构建和检测学习计划,使得预期的目标、评估方法以及证据在整个单元教学中贯穿实现.
2.6 UbD理论与“平面解析几何”单元教学设计的联系
前文大概念、理解六侧面、基本问题、评估与反馈以及WHERETO元素等为平面解析几何具体的单元教学设计奠定了理论基础.在每一个阶段中都涉及到了其中一个或者多个理论,使得UbD理论与教学设计紧密相结合,与其具体联系如图4所示.
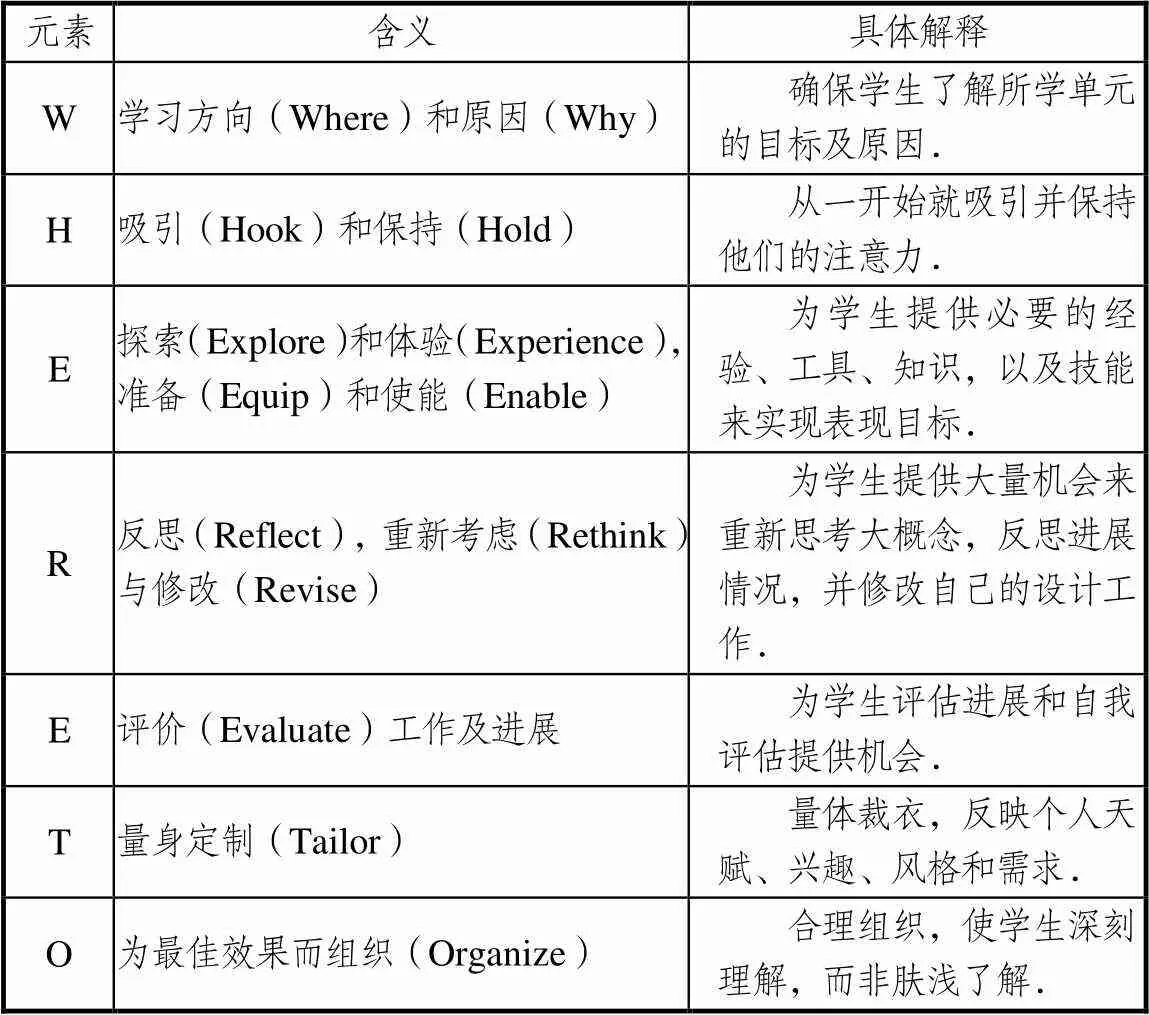
表1 “WHERETO”元素及其解释
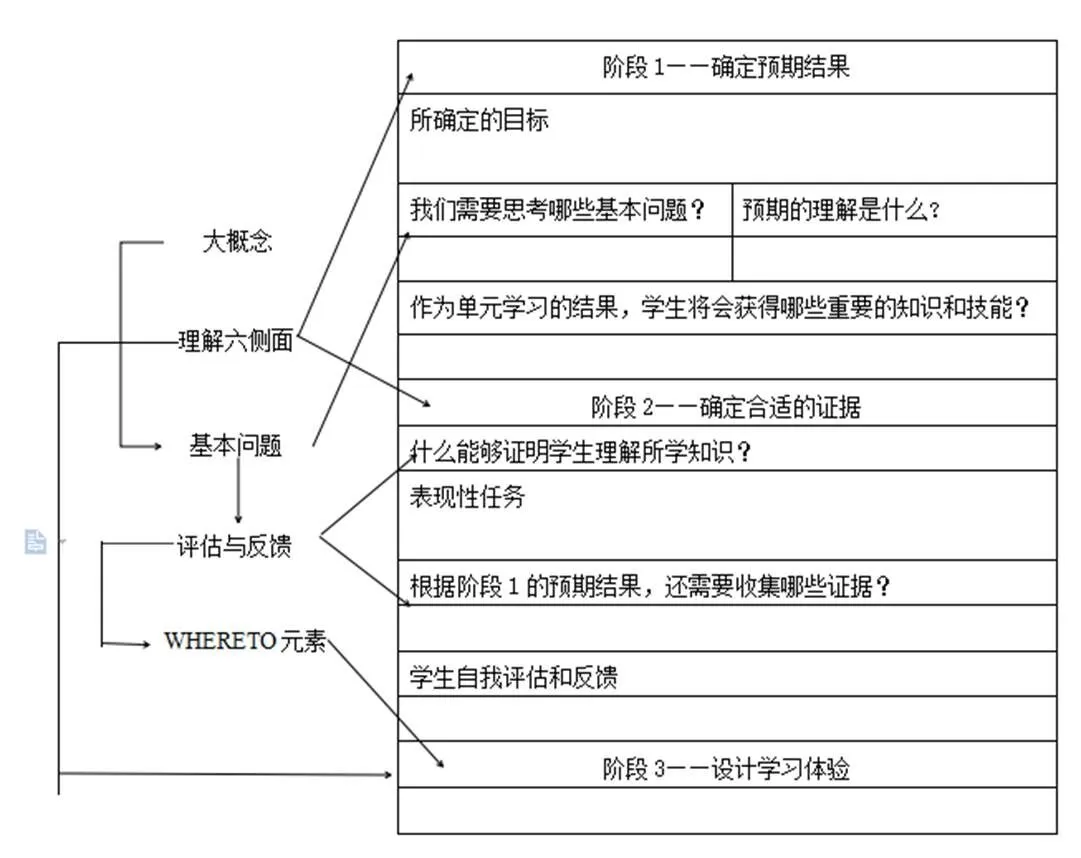
图4 UbD理论与“平面解析几何”单元教学设计的联系
大概念和基本问题为阶段1平面解析几何核心的单元目标以及基本问题提供了理论指导.同时,基本问题的提出也奠定了后继学习的基础.理解六侧面在平面解析几何单元的阶段1基本问题的确立、阶段2评估学生的理解程度以及最后阶段3的实施计划中都有所渗透,使得基本问题、评估和理解三者处于交织循环模式.并且,评估与反馈是平面解析几何教学设计中重要的一环.基于理解的教学设计在对教学过程进行设计的同时,还需将评估渗透在整个教学过程中.根据阶段1确定的基本问题、预期的理解等,再结合评估与反馈的理论,则可设计阶段2中评估所需的证据.最后,WHERETO元素渗透在整个教学活动设计的各个阶段,后继的学习计划以WHERETO中的元素进行具体的活动设计.同时,基本问题以及评估与反馈等理论为最终平面解析几何单元教学设计中WHERETO元素的确立与编排提供了基础,使阶段1和阶段2的各环节在阶段3得以恰当实现.
3 “平面解析几何”逆向单元设计
高中平面解析几何单元内容属于选择性必修课程中的“几何与代数”主题,《普通高中数学课程标准(2017年版)》对于其的基本要求是学生学习平面解析几何,通过建立坐标系,借助直线、圆与圆锥曲线的几何特征,导出相应方程;用代数方法研究它们的几何性质,体现形与数的结合.课标还提出要将数学文化融入课程内容[15–22].根据UbD理论,对平面解析几何单元根据“阶段1——确定预期结果”“阶段2——确定合适的证据”以及“阶段3——设计学习体验”的设计顺序,可以得到平面解析几何的逆向单元教学设计.
3.1 阶段1——确定预期结果
基于平面解析几何中“曲线与方程”这一大概念,利用问题过滤器思考以下问题:平面解析几何单元能给学生带来什么,研究平面解析几何的价值是什么,想让学生理解这一单元的什么内容?平面解析几何在数学学科中起着革命性的作用,其核心在于建立曲线与方程的一一对应关系,为代数与几何之间架起一座桥梁,使得几何代数化、代数几何化成为了解决代数和几何问题的重要思想方法.教学中期望学生能解释“为什么要学习平面解析几何”,能阐明“代数和几何是如何联系在一起的”,能应用“平面解析几何的思想解决问题”,能洞察“两种解决几何问题的方法有什么弊端”.基于上述分析,提出表2中的基本问题与预期的理解.同时,结合《普通高中数学课程标准(2017年版)》对平面解析几何部分的内容提出的要求确定本单元设计中的教学目标.并从上述课程标准出发,结合所确定的目标确定学生通过单元学习获得的知识与技能.
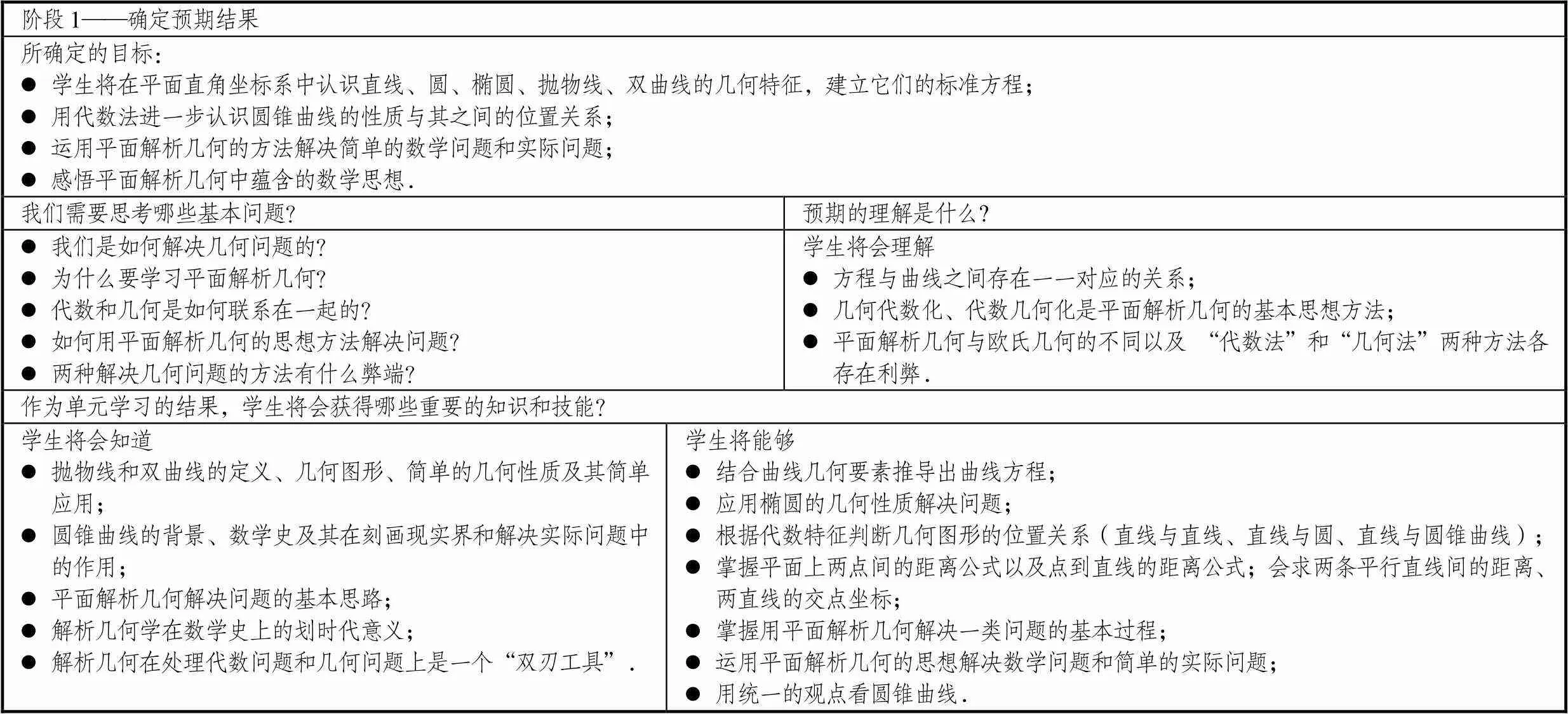
表2 “平面解析几何”逆向单元设计的阶段1设计
3.2 阶段2——确定合适的证据
根据UbD理论,单元设计中的评估方法涉及到了表现性任务、随堂测验、小测验、单元测试、问答题以及自我评估等,如表3所示.对于平面解析几何这一单元而言,学生要掌握的核心任务是掌握用平面解析几何解决几何问题的一般思想与基本思路,辩证地认识“几何法”和“代数法”这两种解决几何问题的基本方法.同时,了解平面解析几何在数学史上的划时代意义以及会运用平面解析几何的思想解决实际问题都是顺应时代的重要学习任务.而对于认识直线、圆、圆锥曲线的几何特征等需要学生熟悉的知识,利用传统的测验和测试评估是有效可行的.
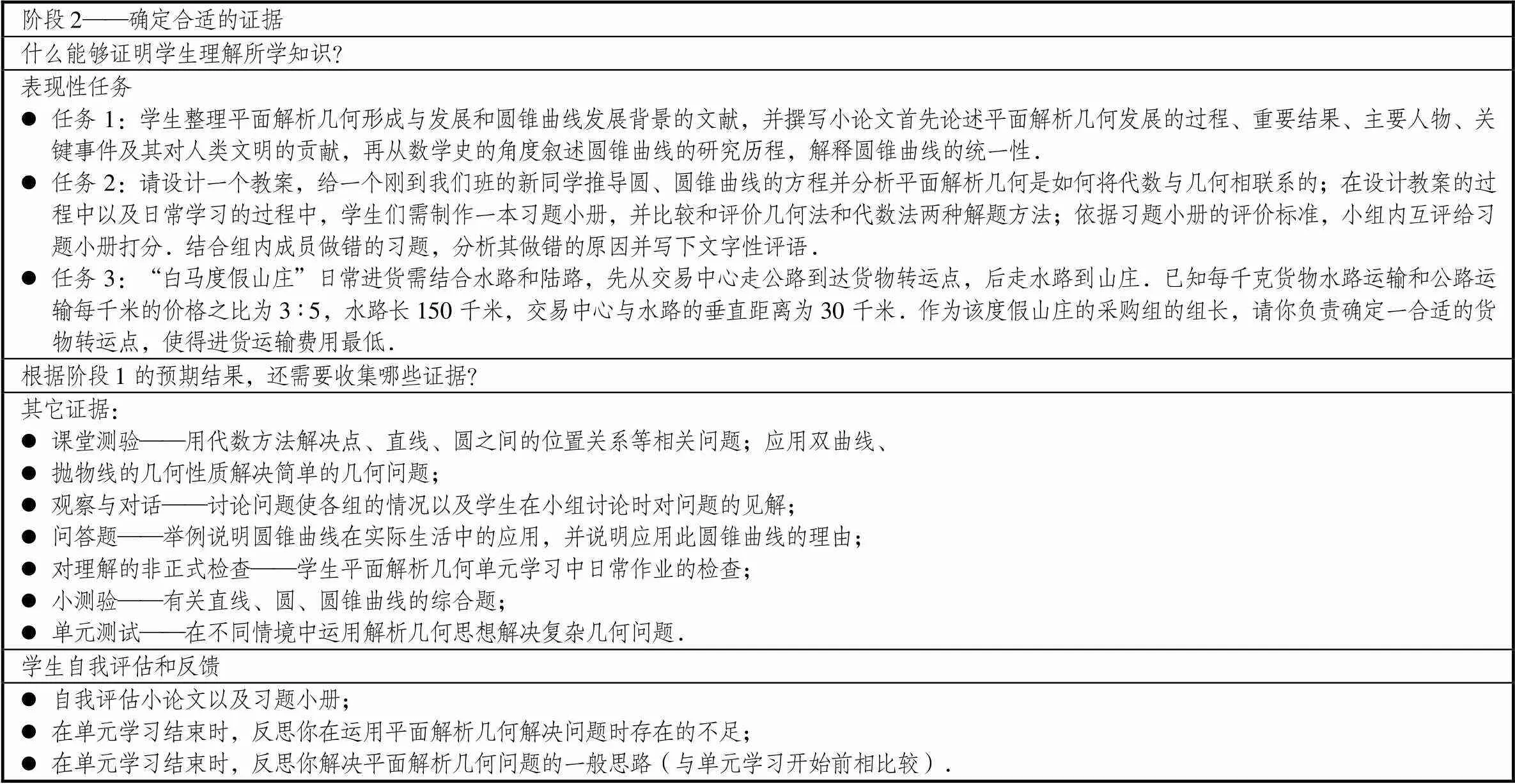
表3 “平面解析几何”逆向单元设计的阶段2设计
在表现性任务的选择上,根据其测评目标的理解侧面可以选择不同类型的表现性任务.表现性任务强调任务与情境的真实性,离开真实情境或任务是无法很好地评价核心素养的[1].如为了给请假未上课的同学补圆锥曲线的课,设计一个教案;阅读平面解析几何的发展史,写成小论文在课上汇报;给项目经理挑选合适的货物转送点,完成一份项目报告等都是具体的基于真实情境的表现性任务.上述表现性任务可以根据理解的多个侧面对学生的知识理解进行评估.并且,基于真实情境的表现性任务是培养学生关键能力、必备品格与价值观念的良好载体.此外,此单元的设计还重视学生的自我评估与互相评估.在反思自身学习过程的基础上,习题小册的互评表不仅能指引学生知道如何学习,通过对他人出错原因的剖析也能对学生神入的理解侧面进行考察.最后,为了保证每一个目标都被评估,设计中需要从后往前逆向推导,所设计的评估任务是否评估了阶段1所提出的所有目标.这时设计者可能发现重要的学习任务会被反复地评估,逆向设计的功能就悄悄地显现出来了.
为了更好地检验学生对平面解析几何单元知识的理解,在阶段2中提出了3个表现性任务.对于这3个表现性任务,研究者又进一步对任务进行深描,考核了学生“对平面解析几何在数学史上的划时代意义、圆锥曲线的背景的了解;会用统一的观点看圆锥曲线;能运用平面解析几何的思想解决实际问题”等目标,对学生应该呈现的表现和作品提出具体的要求和标准,从而更好地实现评估与反馈.
表现性任务1计划
通过这个任务,我们需要对哪些理解或目标进行评估?
学生对平面解析几何在数学史上的划时代意义、圆锥曲线的背景的了解;学生会用统一的观点看圆锥曲线.
不考虑任务的特殊性,在内容标准和理解中隐含哪些准则?学生作品必须呈现哪些品质才能表明他已经达到内容标准的要求?
涉及的历史故事真实;有自己的理解.
通过什么样的真实的表现性任务来证明学生的理解?
任务概述:每一个数学知识的背后都有着深厚的历史底蕴,了解数学史有利于我们对新知识的掌握.通过整理平面解析几何形成与发展的文献,你的目标是撰写一篇论文,论述平面解析几何发展过程中出现的主要人物、关键事件、重要结果及其对人类文明的贡献.并且,你还需要从数学史的角度叙述圆锥曲线的研究历程,解释圆锥曲线的统一性.
学生的哪些作品和表现将为预期的理解提供证据?
小论文.
通过哪些标准来评估学生的作品和表现?
完整的平面解析几何发展过程;准确的重要结果、主要人物、关键事件;恰当的论文格式;能从阿波罗尼乌斯的研究中学会用统一的观点看圆锥曲线.
表现性任务2计划
通过这个任务,我们需要对哪些理解或目标进行评估?
学生对用“几何法”“代数法”解决几何问题的辩证认识;学生对用平面解析几何解决问题的基本思路的理解.
不考虑任务的特殊性,在内容标准和理解中隐含哪些准则?学生作品必须呈现哪些品质才能表明他已经达到内容标准的要求?
评价意见客观中肯;教案设计内容准确;习题册渗透了设计思路;总结精准、到位.
通过什么样的真实的表现性任务来证明学生的理解?
任务概述:由于平面解析几何主要是代数与几何之间关系的转化,最重要的是要明确代数与几何之间是如何转化的.因此,你的目标是设计教案,给新同学讲解代数与几何是如何相联系.此外,我希望你能结合具体的例子,在推导圆锥曲线的方程的过程中将上述关系加以解释.最后,请将你的教案进行汇报和大家分享你的设计思想.
在学习的过程中,我们会做较多的习题,你也可能会有许多错题.你的目标是设计一本习题小册将你做过的习题进行整理,也可以自己补充习题.但是,每题都要尝试有代数法和几何法进行求解,并比较两解法的优缺点.最后,总结运用平面解析几何解决一类问题的基本过程,并对两种方法进行总结评价,帮助今后面对几何问题时做正确的决策.
班级是一个大家庭,同学之间要学会互相帮助.因此,我们需要互评小组成员的习题小册,并帮助你的小组成员分析错题出现的原因.你的目标是根据评价标准完成习题册评价表,给小组成员的习题小册打分并写上评语,为你的小伙伴提供建议.
学生的哪些作品和表现将为预期的理解提供证据?
教案;习题小册、习题小册评价表.
通过哪些标准来评估学生的作品和表现?
教案设计的合理可行、教学思路有逻辑、方程推导过程正确;习题小册有设计感:习题有选择性的分版块总结、解题过程规范,选择的习题典型且有创新;在习题小册的总结评价中能领会平面解析几何思想的本质,能深刻认识到自己的理解局限,并有见地的把握代数法、几何法;具有开放的态度理解别人的解题过程,并能提出中肯的建议.
表现性任务3计划
通过这个任务,我们需要对哪些理解或目标进行评估?
学生能运用平面解析几何的思想解决实际问题;学生会掌握运用解析几何解决一类问题的基本过程.
不考虑任务的特殊性,在内容标准和理解中隐含哪些准则?学生作品必须呈现哪些品质才能表明他已经达到内容标准的要求?
方案具有可行性(时间、地理环境).
通过什么样的真实的表现性任务来证明学生的理解?
任务概述:数学与生活是紧密联系的.“白马山庄”的日常进货需水陆结合,先从交易中心走公路到达货物转运点,后走水路到山庄.已知每千克货物水路运输和公路运输每千米的价格之比为3∶5,水路长150千米,交易中心与水路的垂直距离为30千米.作为该度假山庄采购组的组长,你的目标是确定一合适的货物转运点,使得进货运输费用最低.此外,还需要写一份报告给山庄的总经理,解释你的货物转运点是怎样达到进货运输费用最低的要求的,说明货物转运点的地理位置.并且附带一张图表,说明你分析解决此问题的过程.
学生的哪些作品和表现将为预期的理解提供证据?
转运站的位置;给总经理的报告.
通过哪些标准来评估学生的作品和表现?
准确建立数学模型;合理解释货物转运点的入选理由;结合图表规范表达;恰当的报告格式.
3.3 阶段3——设计学习体验
根据逆向教学设计的理念,教学的目标和评估应先行.确定好教学目标和评估之后,基于上述确定的目标和评估即可开展阶段3学习体验的设计.
阶段3根据“WHERETO”元素将阶段1中提到的基本问题以及阶段2中的评估任务进行编排,使其逐步得到实践,如表4、表5所示.

表4 “平面解析几何”逆向单元设计的阶段3设计
在阶段3的设计中,设计者要清楚地明白两个问题:给定了预期目标后学生要做什么;给定了表现目标,如何对课内外时间做最有效的安排.设计的基本思路如下.第一,追本溯源平面解析几何的历史发展让学生明白为什么要学习平面解析几何以及平面解析几何的核心思想:建立点与坐标之间的一一联系;第二,再从学生熟悉的平面几何图形直线与圆入手,师生共同探索点、直线、圆等简单几何图形的方程与位置关系,初步感知平面解析几何的思想;第三,在反思与总结的基础上,借助圆锥曲线的几何特点,经历探索圆锥曲线的方程与简单的几何性质过程,形成用平面解析几何解决几何问题的一般思路;第四,学生需要了解圆锥曲线在生活中的实用价值,并会利用平面解析几何的思想解决实际生活中的问题,发展数形结合、化归转化的数学思想,培养直观想象、逻辑推理、数学建模的数学素养.
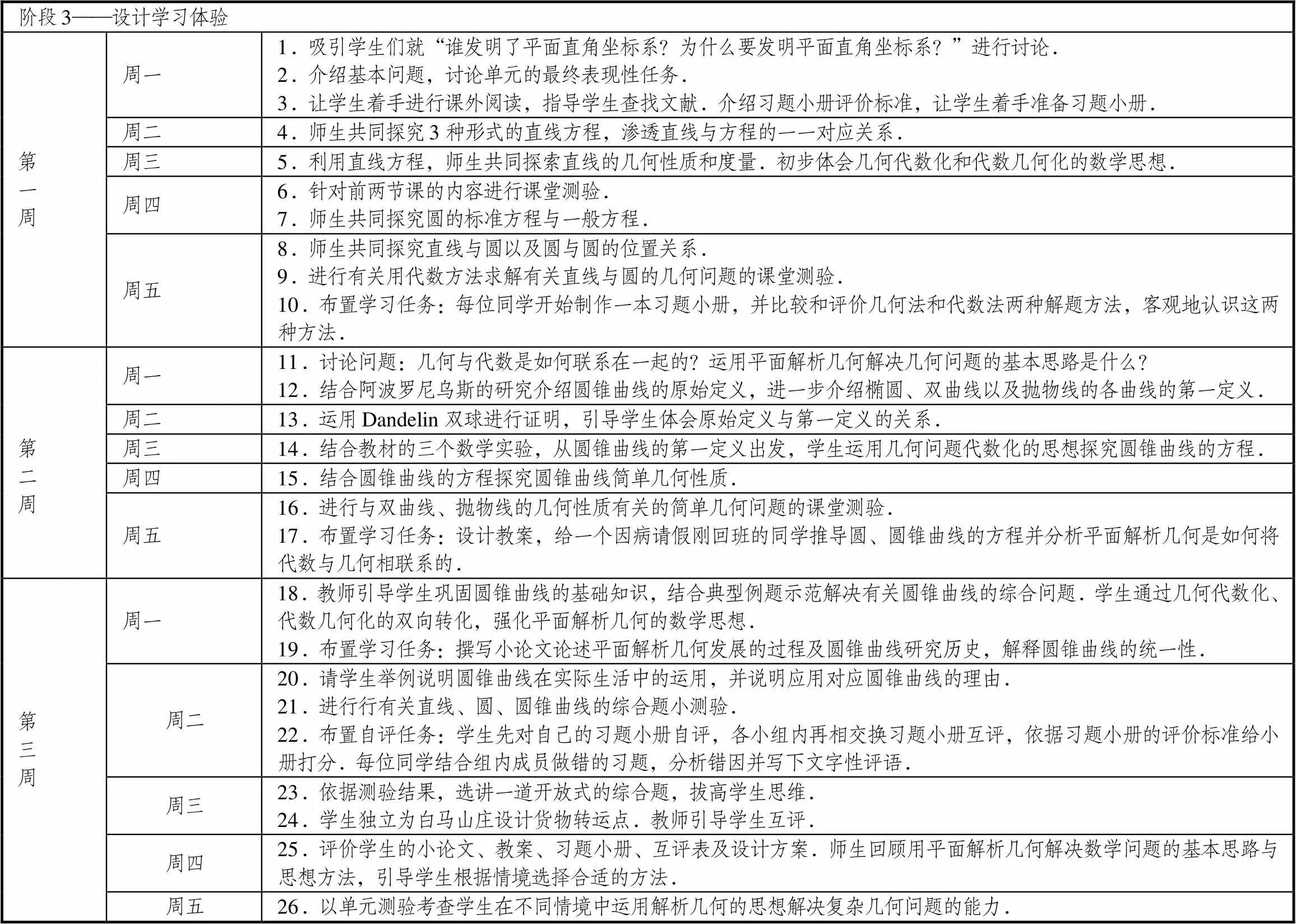
表5 “平面解析几何”逆向单元设计阶段3的时间计划
在以上4步的大框架下,设计者在恰当的时间节点处放入评价任务,确保学生有足够的能力适应学习任务.与传统教学设计的不同之一在于基于UbD的学习体验的设计不只考虑到了学与教,还将教、学、评三者的一致性放到了重要的地位;其二在于该设计充分考虑到了学生能力、品格与观念的培养,真实情境的评价与学后反思的自我评估双管齐下,实现了知识、技能、情感态度价值观到学科核心素养的跨越.
基于UbD的学习计划可以落实到每一天的教学中,此平面解析几何的单元设计可以在3周内完成.在此学习计划中共涉及1个W元素,1个H元素,6个E元素,3个R元素,7个E-2元素,3个T元素以及3个O元素,使得整个教学覆盖了学生的思考、探究、组织、体验、反思以及评价反馈等多方面,形成了一个有效且学生参与性强的学习计划.同时,上述WHERETO元素还有助于教师设计以培养核心素养为目标的学生活动,其涉及面的广度和深度可为教师完善学生学习活动的全面性提供借鉴.
4 启示
基于UbD理论的教学设计是可操作的,UbD单元教学设计并不只是停留在观念层面,它不是难以实现的理念.大概念、理解六侧面、基本问题、评估与反馈、WHERETO等为单元教学设计奠定了坚实的理论基础,使其在真实教学中可以扎实有序地推进.更重要的是,基于UbD理论的教学设计对数学课程、学生和教师的发展有着重要作用.
(1)基于UbD理论的教学设计是对传统教学设计的重构.
UbD的设计并不是对传统课程的颠覆,而是对传统课程的有序重构,充分契合了课程的结构体系和学生的认知发展,呼应了现在亟待落实的核心素养.基于UbD的教学设计是对现有课程的创新改造,随着学习计划的推进,学生对该单元的掌握在交替的学习与评估中逐渐深入,体现了学习体验、学习评估、自我修正三者不断调适交织的的动态过程.但UbD的设计并不完全与传统教学相左,并不排斥传统的考试与测验的评估方式,获得新知之后的及时测试是必要的,纸笔测试在整个单元设计中的作用同样不可忽视.
(2)基于UbD理论的教学设计使得课程实践设计整体化、连续化.
UbD设计是以教学目标为导向的逆向设计,可以应用于一节课、一个单元以及一门课程,使得课程的设计趋于整体化.UbD单元设计可以从整个单元出发安排整个教学,使得学生能连贯地学习有关知识.例如,平面解析几何单元设计对原教材中的教学内容编排顺序进行调整,将整个平面解析几何内容的教学一气呵成.并且,UbD设计中阶段2的评价方法以及证据来源于阶段1的教学目标,通过信效度的检验保证目标与评估的一致性.两个阶段又共同决定了阶段3教学过程的设计.反过来,阶段3的教学过程使阶段1的目标和阶段2的评估方法和证据得到实现.因此,UbD设计的3个环节紧密联系,环环相扣,使得整个设计形成有机的整体,学习、评估、教学三者达到很强的一致性.
(3)UbD理论的教学实践落实学生核心素养,促进教师专业发展.
在基于UbD理论的课堂实施中,教师更加重视思想方法的渗透以及对学生高层次数学思维和能力的培养,这与时代呼应的培养学习者的技能完美融合.学生在整个学习体验过程当中,在问题中成长,经历真实情境,完成具有挑战性和可能性的真实任务.学生在学校的学习中获得了发展21世纪必备品格与关键能力的机会,从而培养了其核心素养.
另一方面,在这样的课程中教师既是设计者又是评估者,还是监测者.首先阶段1的设计要求教师对数学学科的知识有基本的把握,能精准地找到该单元设计中蕴含的大概念.其次,在教学材料的选择上,要求教师自己的学生有足够地了解,基于学情制定评估任务、确定相应的学习材料.特别地,如何围绕所教的数学知识为学生创造一个真实的、必要的而非虚造的表现性任务是有挑战的.最后,在阶段3的学习计划真正实施时,由于单元设计覆盖的知识点具有连贯性,因此教师对整个单元设计需要有宏观地把握.考虑到一些学习任务的复杂性(如习题小册的互评),教师需要灵活地组织管理,时时跟踪学生的学习进度,依据学生当下的表现调整整个单元设计的进程,确保学生的学与教师的教指向学生的理解.在这样循环往复的进程中,教师对单元或者课程的把握逐渐深入,UbD理论的实践过程促进了教师的专业发展.
[1] 崔允漷.如何开展指向学科核心素养的大单元设计[J].北京教育(普教版),2019(2):11-15.
[2] 加德纳·霍华德.多元智能[M].北京:新华出版社,1999:10.
[3] BRANKSFORD J, BROWN A, COCKING K. How people learn: Brain, mind, experience and school [M]. Washongton DC: National Research Council, 1999: 42-56.
[4] 崔允漷.指向学科核心素养的教学即让学科教育“回家”[J].基础教育课程,2019(Z1):5-9.
[5] 莱斯利·P·斯特弗,杰里·盖尔.教育中的建构主义[M].高文,徐斌艳,陈可拉,等译.上海:华东师范大学出版社,2002:50.
[6] 特威金·斯美格兰,杰伊·麦克泰.追求理解的教学设计[M].上海:华东师范大学出版社,2017:36-231.
[7] 邵朝友,崔允漷.指向核心素养的教学方案设计:大观念的视角[J].全球教育展望,2017,46(6):13-21.
[8] 李刚,吕立杰.大概念课程设计:指向学科核心素养落实的课程架构[J].教育发展研究,2018,38(Z2):41-48.
[9] 陈明选,邓喆.围绕理解的学习评价——基于SOLO分类理论的视角[J].中国电化教育,2016(1):71-78.
[10] JABLONKA E. Mathematical literacy [J]. Second International Handbook of Mathematics Education, 2003, 9 (4): 33-34.
[11] BARROWS H S, KELSON A C. Problem-based learning in secondary education and the problem-based learning institute [J]. Springfield IL: Problem-Based Learning Institute,1995, 1 (1): 1-5.
[12] SAVERY J R, DUFFY T M. Problem-based learning: An instructional model and its constructivist framework [J]. Educational Technology, 1995, 35 (5): 31-38.
[13] NEWMANN F, NEWMANN E, NEWMANN M, et. al. Authentic achievement: Restructuring schools for intellectual quality [M]. San Francisco: Jossey-Bass Publishers, 1996: 30.
[14] MARZANO R, PICKERING D, POLLOCK J. Classroom instruction that works: Research-based strategies for increasing student achievement [M]. Alexandria, VA: Association for Supervision and Curriculum Development,2001: 25.
[15] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018:43-46.
[16] 黄翔,童莉,李明振,等.从“四基”“四能”到“三会”——一条培养学生数学核心素养的主线[J].数学教育学报,2019,28(5):37-40.
[17] 李红云,朱文芳,伍春兰.学生统计思维发展水平划分探究[J].数学教育学报,2019,28(5):41-46.
[18] 邓清,夏小刚.数学思维视域下“教表达”的再认识与思考[J].数学教育学报,2019,28(5):47-50.
[19] 吴宏,张珂,刘广军.数学写作融入初中数学教学的实验研究[J].数学教育学报,2019,28(5):51-58.
[20] 渠东剑.素养导向下的学业质量评价探讨[J].数学教育学报,2019,28(5):59-64.
[21] 郑毓信.“数学深度教学”的理论与实践[J].数学教育学报,2019,28(5):24-32.
[22] 朱先东.指向深度学习的数学整体性教学设计[J].数学教育学报,2019,28(5):33-36.
Instructional Unit Design Based on UbD Theory: Using Analytic Geometry as an Example
GE Li-ting1, SHI Meng-yuan2, YU Guo-wen3
(1. Hangzhou Middle School of Hangzhou, Zhejiang Hangzhou, 310002, China;2. Xiamen No.1 Middle School of Fujian, Fujian Xiamen, 361003, China;3. Basic Education Teaching Research Center, Beijing Academy of Educational Sciences, Beijing 100036, China)
Units design based on UbD is a gentle and orderly reconstruction of the current curriculum system. Combined with big concepts, six aspects of understanding, basic issues, evaluation and feedback, and WHERETO elements, we conducted instructional unit design based on UbD theory. The design of analytic geometry based on UbD aimed to provide a reference for mathematics educators who are trying to explore how to design large units of high school mathematics curriculum. UbD-based unit teaching is operable and a reconstruction of traditional teaching. It enables the curriculum design to be integrated and continuous and promotes the professional development of teachers while cultivating students’ key competencies.
UbD theory; teaching unit design; analytic geometry
G427
A
1004–9894(2020)05–0025–07
葛丽婷,施梦媛,于国文.基于UbD理论的单元教学设计——以平面解析几何为例[J].数学教育学报,2020,29(5):25-31.
2020–04–22
北京教育科学研究院专项课题——儿童立场的小学数学教材评价研究(0101112000053/005)
葛丽婷(1995—),女,浙江东阳人,硕士,主要从事数学教育研究.于国文为本文通讯作者.
[责任编校:张楠、陈汉君]
