基于OECD“学习框架2030”的初中数学课程内容分析及其启示

董连春，魏 航，孙彬博，曹一鸣

基于OECD“学习框架2030”的初中数学课程内容分析及其启示

董连春1，魏 航2，孙彬博2，曹一鸣2

（1．中央民族大学 理学院，北京 100081；2．北京师范大学 数学科学学院，北京 100875）

对OECD数学课程内容图谱分析的内容框架进行分析和解读，并结合中国《义务教育数学课程标准（2011年版）》进行对比分析．在此基础上讨论数学课程内容图谱分析的内容框架对中国义务教育数学课程标准修订的启示，并从数学课程组织结构、内容选择和编排等方面提出相关建议．

OECD“学习框架2030”；数学课程图谱；初中数学课程；课程改革

课程是影响教育和学习质量的决定性因素，不仅影响着教育系统的正常运转，同时也决定着人才培养能否适应未来国家和社会发展的需求．如何平衡新内容与传统课程内容比例，优化数学课程内容设置，降低学校数学课程知识与未来社会发展需求之间的落差，成为世界各国数学课程改革都面临的两大挑战．OECD发起了国际课程分析（International Curriculum Analysis）项目，依托OECD2030项目（The Future of Education and Skills 2030 Project），基于面向2030所需的4种知识：学科知识、跨学科知识、认知知识和程序知识，建立课程知识基础，从而帮助各个国家和地区更加系统化地开展课程设计．

课程内容图谱分析（curriculum content mapping，简称CCM）[1]是国际课程分析研究中的核心研究之一，旨在为课程比较提供重要的基准数据，对未来的课程开发提供重要参考．这里围绕CCM项目，聚焦数学学科领域，解读课程内容图谱分析项目中数学学科领域的内容框架，采用质性文本分析方法对《义务教育数学课程标准（2011年版）》[2]进行编码研究，分析中国初中阶段数学课程的对比结果，并在此基础上讨论课程图谱分析项目内容框架及其对比结果对中国初中数学课程发展的启示．

1 CCM数学内容主题框架

课程图谱分析项目的目标教育层级包括国际教育标准分类ISCED Ⅱ的所有年级，相当于中国的初中阶段．为了确保选定的项目包括世界不同区域（即亚洲、欧洲、北美和大洋洲等）的课程模式，OECD课程内容图谱分析项目专家对亚洲、北美洲、欧洲、大洋洲的5个国家和地区现有的课程进行调查，同时结合OECD学习框架2030，最终形成内容主题框架（learning area coding framework）．

考虑到不同国家课程标准与教材的具体内容和详略程度差异较大，数学内容主题框架并没有按照完整的知识体系进行编排，而是给出了7类内容主题和31项子主题，以便于各个国家根据自己的课程与教材情况进行灵活处理．内容主题框架旨在反映数学学习主题而非能力．其中特别增加了一些国家在其课程中强调的一些重点内容，以评估其他国家或地区在其课程中对这些内容项目的重视程度．

数学学科内容框架共7类内容主题，包括：（1）数（number）；（2）测量（measurement）；（3）数据和概率（data and probability）；（4）表达式、方程和代数（expressions, equations and algebra）；（5）函数（functions）；（6）几何（geometry）；（7）数学通识部分（general description, where relevant）．上述内容主题共包含31项子主题．

1.1 数

“数”中包含7项子主题，子主题编码与具体内容如表1所示．

表1 内容主题“数”所含子主题

用数轴表示数字的形式意义包括在数轴上表示正负整数、分数、无理数，以及数的运算．借助数轴理解实数的意义，从直观的角度形象地展示数及其关系，能够加强数与形的关联，同时因为它不涉及使用实物材料，也能帮助学生建立数学抽象．国际上很多国家均在初中课程标准中设置数轴表示数的知识，如新加坡、澳大利亚和美国等国家要求学生在数轴上表示有理数，近似地表示无理数，表示有理数的运算，对实数进行排序等[3–5]．从整数扩充到有理数和无理数，再扩充到复数的变化过程，能够促进学生加深对数的认识和理解，同时也会拓展对运算法则和运算律的认识．实数知识包括对负数和无理数的认识和理解，使用有理数估计无理数，实数的四则运算等．复数是在实数基础上对数系的再一次扩充，将代数与几何知识联系起来，主要包括复数的概念、基本运算和几何意义等．问题解决中的运算策略主要包括学生在解决与实数有关的问题时，结合具体问题情境理解数字的含义，并建立不同数字之间的关系．这里的运算策略，并非狭义的“算得对、算得快”，而是注重学生对运算对象、法则、思路和方法的理解和灵活运用．

比例，百分数和比包括比例、百分数和比的概念，比例数量关系的识别与实际应用，解决与百分数和比相关的实际问题．这部分内容建立在分数、小数、除法等知识与技能的基础之上，对培养学生的比例思维（proportional thinking）或比例推理（proportional reasoning）具有重要作用．比例思维涉及对存在乘法关系的数进行比较，深层次理解数量之间关系等[6]．向量包括概念、运算、坐标表示，在几何与实际问题上的应用等．向量是一种新的运算对象，但又与数的运算有密切的联系．学习向量的含义、运算法则和运算规律，有利于拓宽学生对运算对象的认识，帮助学生重新审视数的运算法则和规律．虽然向量既是代数研究对象，又是几何研究对象，但是很多国家的数学课程标准中将向量知识和数的知识归为一类，例如美国数学课程标准将实数系、复数系、向量与矩阵知识归为一类[5]．已有研究发现九年级学生已经可以较好地接受向量的基本知识[7]．国际上一些国家在初中阶段设置向量知识的学习，例如新加坡初中三/四年级要求学生掌握平面向量的基本知识，包括向量的表示方法，向量的加法、减法、数乘运算，向量的分解，以及解决与向量有关的问题[3]．

1.2 测量

“测量”中包含一项子主题，子主题编码与具体内容为：MME1度量单位和比例尺．其中，度量单位涉及基本的度量单位及其换算、量感（measurement sense）的培养，以及一系列平面图形和立体图形的度量，同时涉及到其它的量的度量，例如角度和时间等．比例尺知识主要涉及到地图比例尺．大部分国家在小学阶段对度量单位的使用和换算知识进行了初步介绍，例如长度单位米、厘米等，因此在初中阶段主要涉及较为复杂的度量单位的使用和换算．量感是度量知识中的重要内容，要求学生根据具体情境选择合适的度量单位．在进行测量时，学生需要识别并使用适当的度量单位，选择适合问题的属性（例如长度、面积、温度），选择合适的测量工具以及选择适合具体情境的单位．比例尺，包括按比例绘制几何图形，根据比例尺计算实际图形的长度和面积，根据不同的比例尺绘制图形[3]．

1.3 数据与概率

数据与概率部分凸显了数据这一核心关键词，重点围绕如何收集数据，如何整理数据，如何分析数据，及其相关的概率知识．“数据与概率”中包含7项子主题，子主题编码与具体内容如表2所示．

随机抽样包括随机抽样的含义以及使用随机抽样解决问题的原理和过程．随机抽样是获取数据样本的重要手段，涉及随机性、样本与总体的关系等，是培养学生统计素养和统计推理的重要部分．数据的整理、展示和解读包括统计图表的类型和绘制方法，不同统计图表的使用目的和适用情境，利用统计图表展示和分析数据．这部分内容涉及数据收集之后对数据进行直观呈现和初步理解，是描述性统计的重要组成部分．随机过程与概率模型包括：随机现象与随机事件、简单随机事件可能的发生结果、随机事件的概率、随机事件概率的运算法则、随机事件的独立性、古典概型、伯努利概型、几何概型．数据的集中趋势和离散程度包括平均数、众数、中位数、百分位数、极差、四分位距、标准差的含义与使用．线性模型与双变量关联（和相关）包括成对数据的相关性，一元线性回归模型的含义、方法与应用．这部分主要涉及成对数据，包括对数据进行分析推理并理解数据中所包含的信息等．

表2 内容主题“数据与概率”所含子主题

1.4 表达式 方程 代数

“表达式、方程和代数”中包含5项子主题，子主题编码与具体内容如表3所示．

表3 内容主题“表达式 方程 代数”所含子主题

表达式、方程和代数部分的核心是代数思维（algebraic thinking）和代数推理（algebraic reasoning）包括对数字及其运算进行一般化的抽象，构建符号表达，使用符号表达和探索数量关系与变化规律等．

使用模式表示关系主要涉及符号表示数量关系，例如，使用第项表示规律与关系，使用符号表示离散类型的线性关系等．代数表达式包括代数式的表示和求值、代数式的运算、整式与分式、因式分解．代数式的学习是学生建立符号意识的重要过程，是学生进行数学表达和数学思考的重要基础．根式与多项式是比较常见的代数表达式，这两部分知识的学习对学生在初中阶段建构代数知识体系具有重要作用．根式知识以根号符号为基础，包括根式的概念、意义与运算．多项式内容包括一次多项式、二次多项式、高次多项式的含义与运算、求值、因式分解，二项式，代数恒等式．线性方程与不等式包括一次方程与不等式、二次方程与不等式和不等式组．

1.5 函数

“函数”中包含4项子主题，子主题编码与具体内容如表4所示．

其中，使用函数对关系进行建模包括函数的概念，函数关系的识别、表示和应用，以及简单的函数类型，构造函数表示对两个变量之间的线性关系，通过数量关系图象描述数量关系所满足的函数关系及特征等．

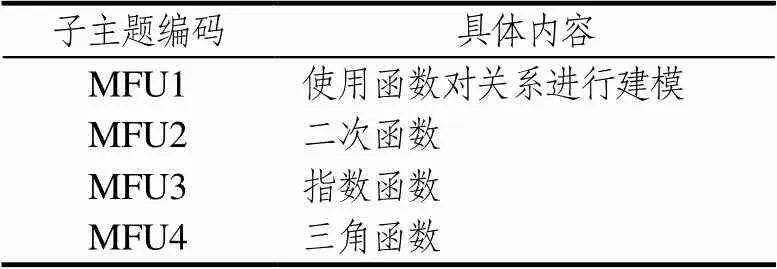
表4 内容主题“函数”所含子主题

二次函数、指数函数和三角函数包括这些函数的定义、图象、性质和使用．例如，通过抛物线图象来认识二次函数及其性质；使用相似性探究直角三角形中的锐角三角函数关系（正弦、余弦和正切）；利用单位圆定义三角函数并画出三角函数图象，研究三角函数的对称性、周期性及其与周期运动的关联，并利用任意角的三角函数知识解决设计和勘测的相关问题等．

1.6 几何

“几何”中包含3项子主题，子主题编码与具体内容如表5所示．

表5 内容主题“几何”所含子主题

空间关系—平面几何和立体几何的定理和性质包括点、线、面位置关系及其相关的定理和性质，平面图形和立体图形相关定理与性质．很多国家数学课程中涉及了空间关系．例如，新加坡涉及角、平行线、三角形、特殊四边形、正多边形、圆及其相关的定理与性质[3]．几何旋转与变换包括平面与空间中图形之间的关系，是几何学习的重点．很多国家数学课程中对这部分做了详细要求．例如，美国八年级要求学生通过操作验证平面几何变换包括旋转变换、翻转变换、平移变换的性质，理解平面几何图形在一系列放缩变换、旋转变换、翻转变换、平移变换后所得到的图形与原图形全等[5]．

勾股定理是重要的几何定理，在几何学习中具有重要意义，也是各个国家数学课程的重点．例如，澳大利亚九年级学习勾股定理及其在直角三角形相关问题中的应用．理解勾股定理可以计算直角三角形中的未知角度和边长；十年级学习使用勾股定理解决空间中与直角三角形相关的问题[4]．美国八年级学习勾股定理及其逆定理的证明，使用勾股定理解决平面和空间几何中与直角三角形有关的边角问题，使用勾股定理极端坐标系中两点间的距离[5]．

1.7 通识部分

“通识部分”中包含4项子主题，子主题编码与具体内容如表6所示．

数学家的工作与贡献常常以数学史与数学文化的内容呈现．例如，在数与代数的学习中引入巴比伦数学，学习素数，公因数与公倍数，幂（包括平方根）等知识，引入古希腊毕达哥拉斯学派以及中国古代勾股术，学习勾股定理等．像数学家一样思考并非要将学生培养成数学家，而是创造机会，让学生从事与数学家相似的数学思考和实践活动．数学与实际生活具有紧密联系，例如民族服饰中的几何知识，经济与金融中的数学知识，包括最优购买方式，盈利与亏损问题，零售打折问题，涉及单利与复利的金融决策问题等．

表6 内容主题“通识部分”所含子主题

数学中的道德与伦理逐渐成为国际课程建设的关注点．道德视角下数学知识的一些应用可能并不正当，例如，数学知识被用于枪械制造，核武器与生化武器，以及其它有伤害性和破坏性的产品和工具[8]．强调数学学习中的道德与伦理，可以帮助学生体验和形成道德理解，并将道德理解应用于行动和决策中[9]．例如，在数据和统计的学习中，因为有意和无意而导致的数据失真（distortion），使用不恰当的比较方式或者标准而造成的不公平，审理财务债权和来源．

编程、数据科学、计算思维与数学学习密切相关．信息技术变革对学生未来数学学习提出更高的要求，未来社会的问题解决与计算机编程（编码）、算法设计、数据科学、机器学习密不可分，均以计算思维为重要基础．PISA2021数学素养测评框架也首次将计算思维作为数学素养的一部分，要求学生综合使用数学思维和计算思维做出预测，为论证提供证据，并对不同的问题解决方案进行检验和比较[10]．

全球公民意识和可持续发展教育是国际课程建设的重要内容．例如，数学学习中所涉及的问题情境应当引发学生对关心国内与国际事务的意识．如人口问题和健康问题，等等[3]．同时，学生通过数学学习获得的问题解决能力和推理能力，探索可持续性问题及其解决方案．例如，学生运用空间推理、测量、估计、计算和比较来衡量当地生态系统的健康状况，并为可持续性发展提出建议和措施[11]．数学知识和技能可以对社会、经济和生态系统随时间的变化进行衡量、追踪和量化，而统计知识和统计分析可以借助数据分析结果预测未来变化，进而在决策和采取行动中做出优化选择．

2 CCM数学主题框架与中国初中数学课程匹配分析

结合CCM数学内容主题框架，对《义务教育数学课程标准（2011年版）》第三学段七~九年级的数学课程内容进行匹配度分析．考虑到CCM项目中数学课程包括数学课程标准文件、数学教材等，因此在匹配度分析过程中，研究者还结合了《义务教育数学课程标准（2011年版）解读》，人教版和北师大版初中数学教材以及教师用书．

CCM数学内容主题按照“完全匹配”“部分匹配”“不匹配”进行分类．其中，“完全匹配”是指内容主题全部包含在中国七~九年级的数学课程中；“部分匹配”是指内容主题只是有一部分包含在中国七~九年级的数学课程中，而其余部分包含在中国小学或高中数学课程中；“不匹配”是指内容主题完全不包含在中国七~九年级的数学课程中．

总体分析结果如图1所示．CCM内容框架涉及的31项子主题中，有23项与中国初中数学课程内容相匹配，约占全部知识主题的74%．其中，14项子主题与中国初中数学课程完全匹配，9项子主题与中国初中数学课程部分匹配，即这9项子主题的知识内容只有一部分设置在初中，同时还有其它部分设置在中国小学或高中数学课程中学习．

2.1 完全匹配内容

共计14个子主题与中国初中数学课程内容完全匹配，如表7所示．

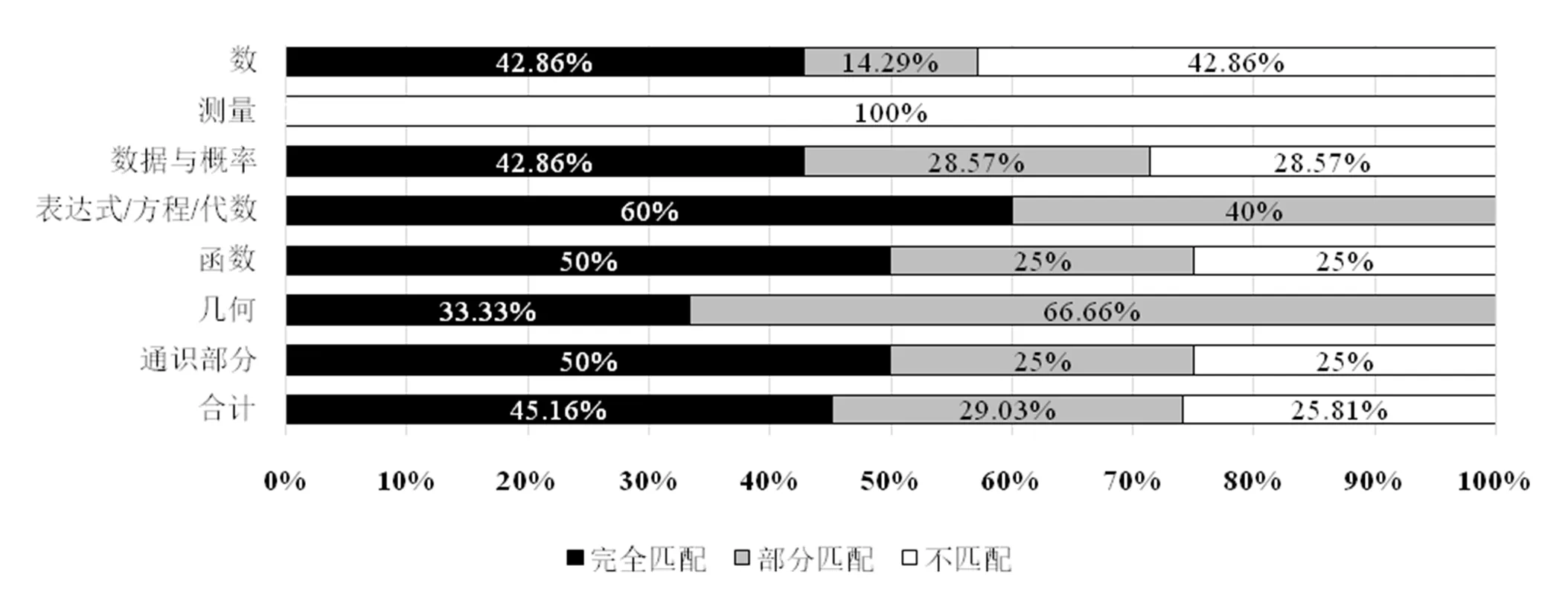
图1 初中数学课程内容与内容框架匹配情况一览

表7 中国义务教育初中阶段数学课程与CCM数学内容主题完全匹配的内容一览

2.2 部分匹配内容

共计9项子主题与中国初中数学课程内容部分匹配，即这些知识主题中的部分内容设置在中国小学或高中数学课程中，如表8所示．

表8 中国义务教育初中阶段数学课程与CCM数学内容主题部分匹配的内容一览

9项与中国初中数学课程内容部分匹配的子主题中，部分内容设置在小学阶段学习的主题有一个，即比例，百分数和比（MNU6），这部分内容的定义、性质及相关计算主要在小学阶段学习．中国《义务教育数学课程标准（2011年版）》中第二学段（四~六年级）“数与代数”部分涉及正比例和反比例内容，要求学生“在实际情境中理解比及按比例分配的含义”，同时要求学生“理解百分数的意义”，解决“百分数的简单实际问题”[2]．

另外8个子主题均有部分内容设置在高中阶段．随机抽样（MDP1）在中国初中数学课程标准中仅涉及简单随机抽样的初步知识，要求学生“体会抽样的必要性，通过实例了解简单随机抽样”[2]．而更加系统地学习在高中进行，要求学生“了解简单随机抽样的含义及其解决问题的过程，掌握两种简单随机抽样方法：抽签法和随机数法”“了解分层随机抽样的特点和适用范围，了解分层随机抽样的必要性”[12]．概率模型（MDP4）在中国初中阶段仅学习一些简单的模型，要求“列出简单随机事件所有可能的结果，及指定事件发生的所有可能结果”，在高中阶段会系统学习古典概型、伯努利概型等模型[12]．多项式（MEA4）在中国初中数学课程标准中仅涉及简单的一次和二次多项式，更复杂的多项式在高中学习．

线性方程与不等式（MEA5）在中国初中数学课程标准中主要涉及一元一次方程、一元一次不等式（组）、二元一次方程（组）、三元一次方程、一元二次方程，而更为复杂的知识如一元二次不等式则在高中学习．二次函数（MFU2）在中国初中数学课程标准中涉及二次函数的图象与性质，使用配方法对二次函数表达式进行变形和分析，用二次函数的图象求一元二次方程的近似解．高中阶段则涉及对二次函数的综合掌握和理解，要求学生“使用一元二次函数认识一元二次方程与一元二次不等式”[12]，空间关系—平面几何和立体几何的定理和性质（MGE1），平面和空间中的几何旋转和变换（MGE2）在中国初中数学课程标准中涉及平面几何部分．而立体几何部分主要在高中阶段学习，例如高中数学必修内容“几何与代数”部分中要求学生“用数学语言表述有关平行、垂直的性质与判定，并对某些结论进行论证”[12]．

与编程、数据科学、计算思维相关的概念（MGE3）在中国初中阶段主要与运算能力相关，要求学生寻求合理简洁的运算途径解决问题．而高中阶段则将“数学运算”作为六大核心素养之一，要求学生“理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果”[12]．

2.3 不匹配内容

31项子主题中，共有8项在初中数学课程内容中不涉及，其中部分主题完全在高中（5项）或小学（2项）学习，另1项完全在其它学科知识中会涉及．具体情况如表9所示．

表9 中国义务教育初中阶段数学课程不涉及的CCM 数学内容主题一览

分数和小数相关问题解决中的运算策略（MNU5）完全设置在中国小学数学课程中，而复数（MNU3）、基于向量的建模和运算（MNU7）则完全设置在中国高中数学课程中．度量单位和比例尺（MME1）完全设置在中国小学数学课程中，中国初中数学课程内容不涉及这部分知识．线性模型（MDP6）、双变量关联（和相关）（MDP7）完全设置在高中数学课程中．指数函数（MFU3）完全设置在高中数学课程中．

与全球公民意识和可持续发展教育相关的概念（MGE4）未出现在中国初中数学课程中，同时中国小学和高中数学课程中也未涉及这部分内容，而是出现在其它学科的课程标准中．例如，中国义务教育地理课程中强调“学生关注自然与社会，使学生逐步形成人地协调与可持续发展的观念”[13]，中国义务教育英语课程中强调“认识世界的多样性，在体验中外文化的异同中形成跨文化意识，增进国际理解”[14]．

3 研究结论

通过分析CCM数学学科内容主题框架，并考察该框架与中国义务教育初中阶段数学课程内容的匹配度，得出如下结论．

3.1 CCM数学内容主题框架突出了学科核心内容主题

CCM数学内容主题框架通过学科核心内容主题组织数学内容结构，凝练了7项内容主题，体现了面向2030背景下OECD课程专家所采取的课程重构原则与方式．数学学科核心主题是数学学习中能够将不同知识内容进行整合的至关重要的思想和主题，在数学学科居于重要地位，并且对数学学科具体内容更具统摄力和关联性．

目前，国际诸多国家在数学课程内容结构上均借鉴了数学学科核心内容主题的理念．例如，新加坡初中数学课程标准提出了8个学科核心内容主题群（eight clusters of big ideas），分别为图示、等价、函数、不变性、测量、模型、符号、成比例，用以将不同的具体数学知识内容进行整合[12]．加拿大不列颠哥伦比亚省数学课程标准提出5个学科核心内容主题：数、运算流畅性、模式化、几何与测量、数据与概率[15]．学科核心内容主题的基本原则是在不同数学知识主题融合基础上的核心概念凝练，强调数学知识之间的联系．课程结构中强调学科核心内容主题可以加强数学知识的连贯性和综合性，有助于学生对知识的综合理解和应用，从而应对未来复杂多变的社会[16]．

3.2 中国初中数学课程内容广度偏小难度偏大

CCM数学内容主题框架与中国初中数学课程内容匹配度研究发现，CCM数学学科框架中仅有45.61%的数学知识主题与中国初中数学课程完全匹配，而与中国初中数学课程部分匹配和不匹配的内容占到54.39%．这意味着，CCM数学学科框架中有超过一半的知识主题并未完全在中国初中阶段设置，而是部分或者完全出现在小学阶段或者高中阶段．与中国初中数学课程内容部分匹配的9项子主题中，有8项为部分内容设置在高中阶段中国初中数学课程内容不匹配的8项子主题中，有5项完全在高中阶学习．这反映出中国初中数学课程知识内容在一定程度上存在广度上偏小、难度上偏大的特点．

3.3 中国初中数学课程在跨学科整合方面存在一定不足

CCM数学学科框架在7类内容主题中，设置了“通识知识”，其中与编程、数据科学、计算思维相关的概念（MGE3）和与全球公民意识和可持续发展教育相关的概念（MGE4）两个二级知识主题，均要求学生将数学知识与其它学科知识进行跨学科整合[21]．而这两个知识主题与中国初中数学课程内容的匹配度结果是部分匹配和不匹配，这反映出中国初中数学课程在跨学科整合方面存在一定程度的上升空间．

4 启示与建议

课程是影响教育和学习质量的决定性因素，因此面对未来的需求和挑战，21世纪的学校课程需要重新定位和调整．CCM数学学科内容主题框架对中国初中数学课程内容的改革和建设提供了借鉴和参考．

（1）在课程内容结构上，凝练学科核心内容主题，突出课程内容主线．

中国初中数学课程结构可以借鉴CCM数学内容主题框架中学科核心内容主题的原则，基于初中阶段的数学知识，提炼核心概念或主题，进而建构数学课程结构．但是需要注意的是，无论是OECD，还是各个国家数学课程标准中，都没有对数学学科核心内容主题的内涵形成统一的认识．普遍的做法是结合各自国家的自身情况和课程建设需求，构建数学学科核心内容主题．基于此，中国初中数学课程中提炼数学学科核心内容主题时，需要在借鉴国际课程建设经验基础上，充分考虑中国数学课程建设的历史经验和优秀传统，结合中国义务教育的实际情况和发展需求，确保中国课程结构中数学学科核心内容主题有效促进基础教育课程改革．

（2）在课程内容选择上，综合考量数学知识主题的广度与难度．

通过与CCM数学内容主题框架进行匹配度分析发现，中国初中数学课程知识内容在一定程度上存在广度上偏小、难度上偏大的特点．这一点在大规模学业测评中也得到了印证．2018年中国义务教育质量监测结果显示，49.4%的八年级学生对数学课程感到很有压力，反映出当前初中数学课程内容使中国学生面临过高的学习压力．而过高的课程压力会进一步对学生数学学业表现、学习兴趣和自信心产生不利影响[17]．与此同时，PISA2018测评结果表明，中国学生数学素养表现世界第一，但是数学学科学习效率为118.0分/时，在参测国家（地区）中排名第46位，从侧面反映出中国学生优异数学学业表现背后所付出的代价，也在一定程度凸显了中国数学课程需要进一步加强在数学内容难度和广度上的考量．因此，中国初中数学课程在改革过程中需要加强对数学课程内容选择的研究，结合中国学生的学习特点和认知发展规律，充分考量数学内容的广度和难度．

（3）在课程内容编排上，重视新兴跨学科内容主题，关注已有数学课程内容是否满足未来社会发展需要，加强跨学科课程整合．

2015年，联合国教科文组织发布《教育2030行动框架》，将教育质量提升作为未来15年世界教育改革的焦点和战略目标[18]，倡导世界各国通过系统性的干预措施和课程改革，提升学校教育系统应对未来复杂形势及多元文化等多重挑战的需求，包括日益复杂的国家与社会各种问题，人口流动、城市化、文化全球化等进程普遍加快，信息、知识的传播渠道和获取方式日趋多元，等等．

未来社会的不确定性和复杂性，要求学生具有更加综合的知识储备和更加宽广的视野，能够将数学知识与其它学科知识进行融合，在非常规的复杂情境中借助数学推理创造性地做出决策[19–20]．OECD在面向2030的知识中指出在理解和解决复杂问题时，跨学科知识变得越来越重要，因此强调学校课程注重跨学科知识的学习．中国初中课程建设需要进一步增强学科之间的交叉和整体性，在设置数学课程内容编排时，充分考虑初中阶段其它学科课程，形成可以用于跨学科整合的知识主题和具有可操作性的具体方案．

[1] 曾再平，孟鸿伟．OECD面向2030的课程图谱分析[J]．基础教育课程，2019（7）：27-33．

[2] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：26-41．

[3] Ministry of education SINGAPORE. Syllabuses of sciences [EB/OL]. (2020-05-22) [2020-06-09]. https://www.moe. gov.sg/education/syllabuses/sciences/.

[4] Australian curriculum, assessment and reporting authority. F-10 curriculum for mathematics [EB/OL]. (2019-02-22) [2020-06-09]. https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/.

[5] Common core state standards initiative. Common core state standards for mathematics [Z]. Washington, DC: National Governors Association Center for Best Practices and the Council of Chief State School Officers, 2010: 58.

[6] CAI J, SUN W. Developing students’ proportional reasoning: A Chinese perspective [M] // LITWILLER B, BRIGHT G. Making sense of fractions, ratios and proportions: 2002 year book. Reston, VA: National Council of Teachers of Mathematics, 2002: 195–205.

[7] GUBRUD A R, NOVAK J D. Learning achievement and the efficiency of learning the concept of vector addition at three different grade levels [J]. Science Education, 1973, 57 (2): 179-191.

[8] ERNEST P. The philosophy of mathematics education today [M] // The ethics of mathematics: Is mathematics harmful. ICME-13 Monographs, 2018: 187-218.

[9] Australian curriculum, Assessment and reporting authority. Ethical understanding [EB/OL]. (2019-02-22) [2020-06-09]. https://www.australiancurriculum.edu.au/f-10-curriculum/general-capabilities/ethical-understanding/.

[10] 董连春，吴立宝，王立东．PISA2021数学素养测评框架评介[J]．数学教育学报，2019，28（4）：6-11，60．

[11] Australian curriculum, Assessment and reporting authority. Sustainability [EB/OL]. (2019-02-22) [2020-06-09]. https://www.australiancurriculum.edu.au/f-10-curriculum/cross-curriculum-priorities/sustainability/.

[12] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：13-50．

[13] 中华人民共和国教育部．义务教育地理课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：3-4．

[14] 中华人民共和国教育部．义务教育英语课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：2-4．

[15] British Columbia, Canada. BC’s new curriculum (mathematics) [EB/OL]. (2019-06-12) [2020-06-09]. https://curriculum.gov.bc.ca/curriculum/mathematics.

[16] TOH T L, KAUR B, TAY E G. Reviewing the past, striving in the present and moving towards a future-ready mathematics education [M] // Mathematics Education in Singapore. Singapore: Springer, 2019: 491-498.

[17] 杨涛，辛涛，罗良，等．义务教育数学教育质量监测的探索与思考[J]．数学教育学报，2018，27（5）：1-7．

[18] 吴凡．面向2030的教育质量：核心理念与保障模式——基于联合国教科文组织等政策报告的文本分析[J]．教育研究，2018，39（1）：132-141．

[19] 曹一鸣，朱忠明．变与不变：PISA2000—2021数学测评框架的沿革[J]．数学教育学报，2019，28（4）：1-5．

[20] 孙彬博，郭衎，邵珍红．PISA2021数学素养测评框架中的“21世纪技能”[J]．数学教育学报，2019，28（4）：12-16．

[21] 曹一鸣，马云鹏，郭衎，等．面向未来的初中数学课程图谱分析——以经济合作与发展组织（OECD）“学习框架2030”为基础[J]．基础教育课程，2020（19）：4-16．

An Analysis and Evaluation of Junior High School Mathematics Curricular Contents Using OECD Learning Framework 2030

DONG Lian-chun1, WEI Hang2, SUN Bin-bo2, CAO Yi-ming2

(1. College of Science, Minzu University of China, Beijing 100081, China;2. Research Center for Mathematics Curriculum and Textbooks of School of Mathematical Sciences, Beijing Normal University, Beijing 100875, China)

This study first introduces and discusses the Learning Area Coding Framework in the OECD Mathematics Curriculum Content Mapping. Then we conducted an analysis of content areas in theusing the Learning Area Coding Framework. The results of the analysis are presented and the implications for the development of the Mathematics Curriculum Standards of Compulsory Education in the next round of mathematics curriculum reform are discussed. Finally, we made recommendations with respect to the structure, content topics, and sequence of content topics.

OECD learning framework 2030; mathematics curriculum content mapping; junior high school mathematics curriculum; curriculum reform

G632.0

A

1004–9894（2020）05–0001–07

董连春，魏航，孙彬博，等．基于OECD“学习框架2030”的初中数学课程内容分析及其启示[J]．数学教育学报，2020，29（5）：1-7．

2020–09–10

经济合作与发展组织（OECD）课程图谱研究项目

董连春（1986—），男，河北沧州人，副教授，主要从事中小学数学课程与教材等研究．曹一鸣为本文通讯作者．

[责任编校：周学智、陈汉君]