泰勒级数法计算静磁场和辐射场强度问题
2020-10-28杨伦
杨 伦
(湖北师范大学 先进材料研究院,湖北 黄石 435002)
0 引言
电动力学是物理学专业核心课程之一,由于涉及的学科知识广、模型公式多、数学理论深、推理计算难,电动力学一直是物理学的重点和难点,现有教学过程中,仍存在对近似解求解重视程度不够的问题[1,2]。物理学中,力学中求解单摆问题、热力学中推导克拉佩龙方程、量子力学中的微扰理论、固体物理中求解晶格原子运动方程等,均广泛利用泰勒级数法[3~5]。本文以电动力学中两道典型问题为例[6],利用泰勒展开法分析同轴线圆形线圈的静磁场和边缘带电荷旋转飞轮的辐射场,有利于加深对稳恒电磁场场强分布和矢量特性的理解,强化了对电偶极矩、电四极矩和磁偶极矩的认识,对电动力学的教学有所裨益。
1 同轴线圆形线圈的静磁场
题目:两个半径为a的同轴线圆形线圈,位于z=±L面上,每个线圈有同方向的电流L.计算轴线上的磁感应强度,求在中心区域产生最接近于均匀的磁场时的L和a的关系(如图1a所示)。
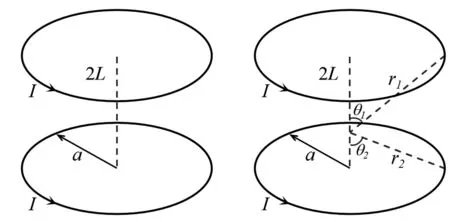
a 同轴线圈 b 轴线角
1.1 计算磁感应强度
磁感应强度的计算是较为简单的,考虑到轴对称性,分别计算2个线圈对轴线上磁场贡献,如图1b所示,引入夹角θ1和θ2,直接利用毕奥-萨法尔定律就可求得:

(1)
1.2 均匀磁场解法一:拉普拉斯算子法

对式(1)计算二阶偏微分得到

1.3 错误解法分析
(2)
1.4 均匀磁场解法二:泰勒级数法

2 旋转飞轮的辐射场
题目:飞轮半径为a,并有电荷均匀分布在其边缘上,总电荷量为Q.设定飞轮以恒定角速度ω旋转,求辐射场(如图2所示)。

图2 飞轮示意图
2.1 常规解法
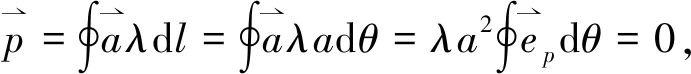
2.2 解法分析
很多学生分析完电偶极辐射和磁偶极辐射,发现均为零,认为题目已经解答完成,该辐射场为零。这种解答方式实际上并不完备,没有考虑电四极矩的贡献,反映出对电磁波辐射问题认识较为肤浅,不够深入,想当然地将电磁波辐射问题作为电偶极辐射和磁偶极辐射的叠加。在解答这道题目之前,需要增强电磁波辐射系统性认识,而不仅仅是简单的记忆电偶极辐射和磁偶极辐射的公式,然后用以结题计算。
回顾辐射场问题,电磁波辐射是源自交变运动的电荷系统,对频率ω0的交变电流,推迟势为
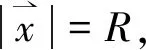
2.3 电四极辐射
Dμ3=D3v=0.飞轮电荷分布相对z轴对称,因此

系统电偶极辐射、磁偶极辐射和电四极辐射均为零,没有这三种类型的辐射场。是否有更高阶的辐射场,在上述计算过程中并不显见,考虑到磁偶极辐射和电四极辐射本就是数量级偏小,更高阶的辐射场更为微弱,现实中很少涉及到。当然,本题目实际上是一种很特殊的情况,我们可以通过普适性分析发现其辐射场为零。
2.4 普适性分析



3 结论
科技发展和现实生活中多数技术问题只能求解近似解,其中最重要的一种方法就是泰勒展开法。本文从电动力学两道典型习题入手,利用泰勒级数法对稳恒电磁场和辐射场场强进行讨论,通过对电磁场具体问题具体分析,增强对矢量场的认识,深化了对辐射场的理解,突出了泰勒展开法在电动力学教学中重要工具性,对学生在物理学进一步学习过程中有一定助益。
