卫星影像在轨定位解算模型构建
2020-10-28丁荣莉谢宝蓉朱浩文张梦琪
丁荣莉,谢宝蓉,王 琰,朱浩文,张梦琪
(上海航天技术研究院,上海 201109)
0 引言
随着遥感技术的发展,卫星影像分辨率不断提高,已经可以达到数十米甚至一米之内[1],影像分辨率的提高利于定位解算技术发展的同时也对定位精度提出更严苛的需求。在轨定位解算技术在无需地面处理的情况下,可以实时提供侦测目标的物理位置信息以实现对动、静目标的定位,可以为一些相关领域的军事及民用项目提供有力的技术支持,如在民用上可以实现渔船等目标的实时跟踪,从而保障出现事故时可及时进行搜救,在军事上可用于对典型目标如船舰、潜艇等定位以及敏感运动目标的运动轨迹跟踪和行为意图的预判,及时有效地建立防御以保障国家领土安全[2-4]。国外定位解算技术相对成熟,文献[5]详细介绍了遥感卫星成像模型中涉及到的主要坐标系并建立了严格成像几何模型。刘世杰[6]探讨了高分辨率卫星遥感影像的各种成像模型,包括严格物理成像模型和有理函数模型等。文献[7]分析了星载线阵CCD传感器严格成像模型的一般建立方法与过程,针对不同的典型高分辨率遥感卫星传感器特点,分别给出了3种改化的严格成像模型。
传统卫星支持作业任务时通常由星上数据获取、星地数传、地面处理和信息分发等环节构成,有效信息到达作战单元的延迟过长,难以满足高动态战场环境感知及战术作战情报信息支持需求。因此,亟需开展在轨处理技术研究以保障信息的实效性。现阶段我国定位解算多是在地面处理计算,而星上在轨定位解算技术发展仍比较空白。本文着重分析了章动岁差、自转和极移对定位精度的影响,并在此基础上优化得到在轨实时定位模型,其算法复杂度相比严格物理成像模型大大降低,符合在轨实现的硬件要求。
1 严格物理成像模型
卫星影像拍摄时刻的像点、投影中心和地面物点这3点满足共线方程,依据3点共线可建立严格物理成像模型[8-9]。模型还涉及到一系列航天坐标系及其相互转换,需要依次建立WGS84坐标系[10]、J2000坐标系[11]、轨道坐标系、本体坐标系、相机坐标系和焦平面坐标系[12]。通过坐标系间的转换,将影像坐标与地面坐标归一到同一参考系下,坐标系变换框图如图1所示。
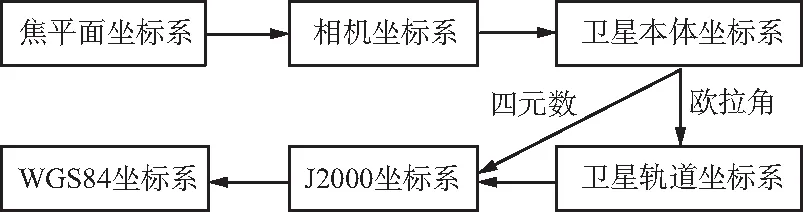
图1 航天坐标系变换框图Fig.1 Transformation block diagram of space coordinate systems
由以上可得严格物理成像模型表达式:
(1)
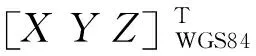
2 星上几何成像模型构建
星上存储资源紧张且感兴趣目标点定位解算实时性要求较高,而严格物理成像模型涉及大量的三角函数运算和矩阵变换,计算资源消耗大且计算耗时长,因此需要对严格物理成像模型进行优化从而得到适用于星上处理的几何成像模型。
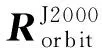
(2)
b3=-s/|s|,
(3)
b2=b3×v/|b3×v|,
(4)
b1=b2×b3,
(5)
式中,s为J2000坐标系中的卫星位置矢量;v为J2000坐标系中的卫星速度矢量。
J2000坐标系到WGS84坐标系的变换矩阵为[14]:
(6)
式中,W(t)为极移矩阵;R(t)为地球自转矩阵;Q(t)章动岁差矩阵。
GPS下传的卫星轨道数据常为WGS84坐标系下的速度和位置,进行定位解算时首先需将WGS84坐标系下的速度和位置转换为J2000坐标系下的速度和位置,即:
sJ2000=[W(t)·R(t)·Q(t)]T·sWGS84=
(7)
vJ2000=QT(t)·RT(t)[WT(t)·vWGS84+we×
(WT(t)·sWGS84)]=
(WT(t)·sWGS84),
(8)
式中,we=7.292×10-5(1-LOD/86 400)。
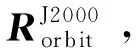
(9)
(10)
由以上可知,定位时J2000坐标系到WGS84坐标系的变换矩阵,以及轨道坐标系到J2000坐标系的变换矩阵表达式中都涉及章动岁差矩阵、地球自转矩阵和极移矩阵及其逆矩阵的求解。而这3个矩阵求解时涉及的角度表达式系数多、运算量大、计算复杂。为降低模型运算量对它们展开具体分析。
2.1 章动岁差矩阵
在J2000坐标系转WGS84坐标系过程中,若不考虑章动岁差影响,则其引起的误差表达式为:
(11)
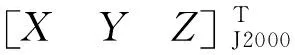
根据式(11)进行Matlab仿真得坐标转换误差,如图2所示。
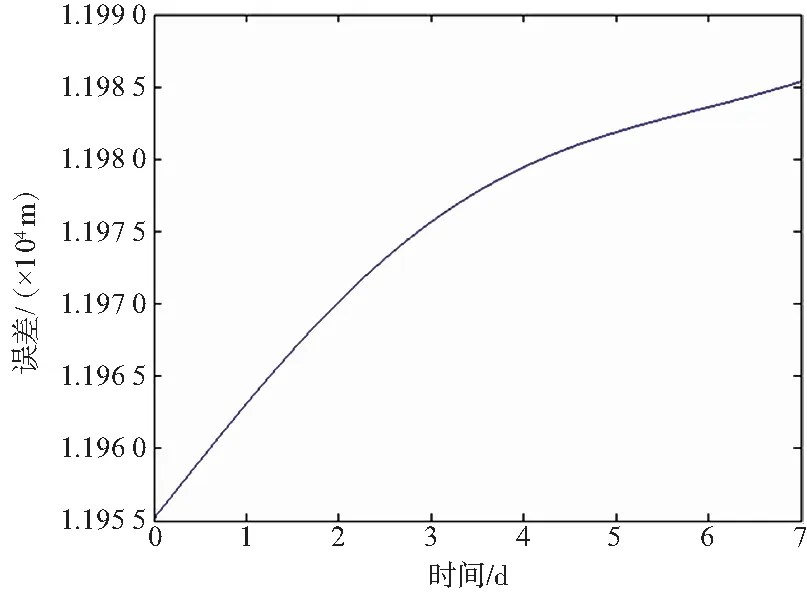
图2 缺省章动岁差对坐标变换影响Fig.2 The effect of default nutation precession on coordinate transformation
由图2可知,J2000坐标系转WGS84坐标系的过程中,在7天观测时间内,章动岁差对J2000坐标系转WGS84坐标系产生的影响峰值超过11.986 km,且呈缓慢增长趋势。故坐标系变换过程中缺省章动岁差对变换结果影响较大,不可忽略。
2.2 地球自转矩阵
在J2000坐标系转WGS84坐标系过程中若不考虑地球自转影响,则其引起的误差表达式为
(12)
式中,d(r)为有无地球自转矩阵引起的距离误差;R(t)为地球自转矩阵。
根据式(12)进行Matlab仿真得坐标转换误差,如图3所示。
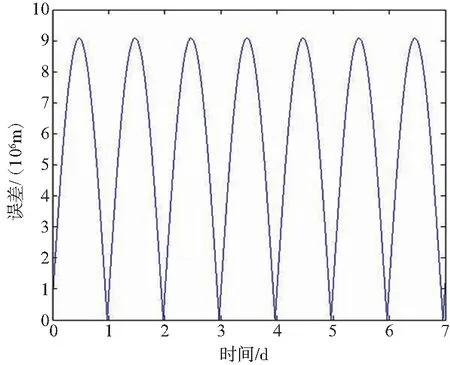
图3 缺省地球自转对坐标变换影响Fig.3 The effect of default earth rotation on coordinate transformation
由图3可知,J2000坐标系转WGS84坐标系过程中,在7天观测时间范围内,地球自转对J2000坐标系转WGS84坐标系产生的影响峰值超过9 000 km。坐标系变换过程中缺省地球自转矩阵对变换结果影响显著,不可缺省自转构成的变换矩阵。
2.3 极移矩阵
在J2000坐标系转WGS84坐标系过程中若不考虑极移矩阵影响,则其引起的误差表达式为
(13)
式中,d(r)为有无极移矩阵引起的距离误差;W(t)为极移矩阵。
根据式(13)进行Matlab仿真得坐标转换误差,如图4所示。
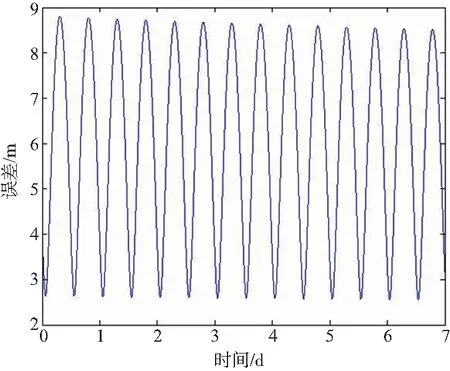
图4 缺省极移对坐标变换影响Fig.4 The effect of default polar shift on coordinate transformation
由图4可知,J2000坐标系转WGS84坐标系过程中,在7天观测时间范围内,极移矩阵对J2000坐标系转WGS84坐标系产生的影响峰值不超过9 m。极移影响较小,为降低算法复杂度可以缺省极移矩阵。
根据以上分析可知,极移矩阵对卫星定位精度影响较小,故可忽略极移影响。将焦平面坐标系下的像素坐标变换到卫星本体坐标系下表示为[X1,Y1,Z1],其表达式为:
(14)
将式(4)带入严格物理成像模型:

(15)
按式(15)进行定位时不仅要求解J2000坐标系到WGS84坐标系的变换矩阵,还需求解其逆矩阵,而章动岁差矩阵和地球自转矩阵和极移矩阵求解复杂,为进一步降低运算量,依据三阶正交矩阵的分配率[15],若|R|=1,则R(B×C)=(RB)×(RC),对模型进行优化。优化后得星上几何成像模型表达式为:

(16)
星上几何成像模型不需要求解J2000坐标系转WGS84坐标系的变换矩阵,且简化了本体坐标系到J2000坐标系变换矩阵形式,大大降低了模型复杂度,为星上在轨处理奠定了基础。
3 实验仿真验证
为验证所构建星上几何成像模型的准确性,采用卫星拍摄的迪拜影像和其对应的GPS接收机输出的轨道位置速度信息以及星敏感器和陀螺组合定姿输出的姿态信息进行仿真分析。迪拜影像成像时间为相对时间,GPS接收机输出WGS84坐标系下的位置和速度,姿态数据以欧拉角形式给出。在影像上随机选取若干像素点进行定位解算,并将定位解算结果与其对应的谷歌地图真实经纬度进行比较求解误差,其结果如表1所示。
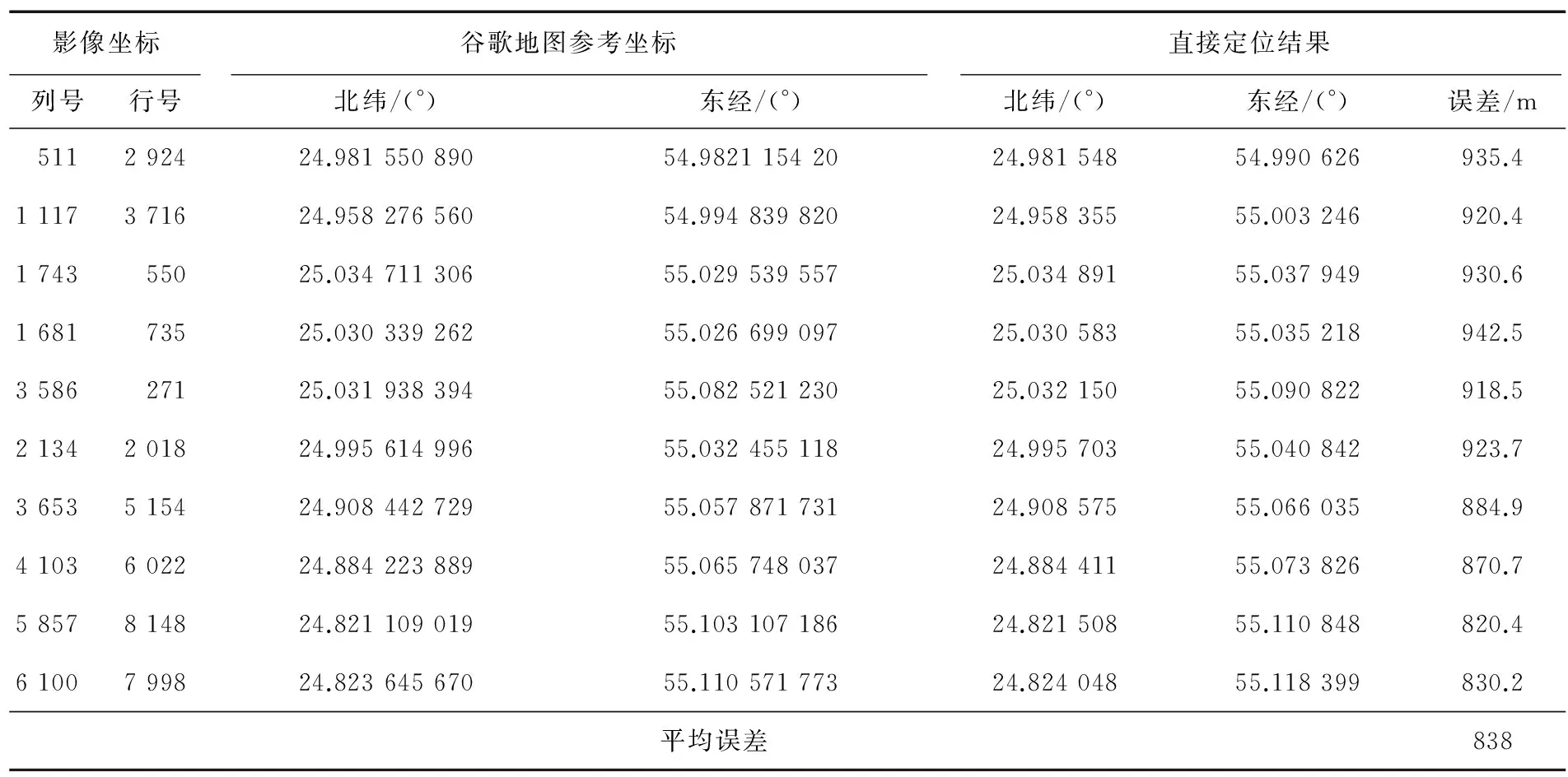
表1 图像直接定位结果Tab.1 Direct image location results
由表1可知,影像的直接定位结果误差均值为838 m,影像各像素点的误差值沿均值分布,可以证实星上几何成像模型构建的准确性。
4 结束语
为节约星地传输资源和保障定位解算的实时性,深入理解严格物理成像模型的原理,分析了章动岁差、地球矩阵和极移对坐标变换的影响,其中极移矩阵对坐标变换影响低于10 m,极移矩阵可忽略不计。再依据三阶正交矩阵的分配率对严格物理成像模型表达式进行优化从而得到星上几何成像模型。星上几何成像模型避免了复杂的J2000坐标系到WGS84坐标系的变换矩阵求解,算法复杂度明显降低。同时经卫星拍摄的影像进行定位解算验证,未定标定位误差均值为838 m,星上几何成像模型的构建准确。虽然直接定位误差结果相对理想,但仍不能满足高分辨率卫星定位精度的需求,因此定位解算的在轨定标技术是未来需要继续研究的课题。
