不同蒸散发模型在湿润地区的适用性研究

马俊超，李琼芳，黄晓敏，徐成剑

(1.长江勘测规划设计研究有限责任公司，湖北 武汉 430010； 2.河海大学 水文水资源学院，江苏 南京 210098)

蒸散发是水文循环的重要过程，也是水量平衡的重要组成部分。准确估算区域蒸散发量对于农业灌溉预测及水量合理分配具有重要意义。早在1948年，Penman就基于大气动力平衡方程和湍流扩散理论，将空气动力学和热量平衡方程进行结合，提出了著名的Penman公式[1]。Monteith又在1965年对该公式进行了改进，加入植物叶面气孔扩张程度以及植物表面对水汽的扩散阻力，并采用植物冠层阻抗计算水汽分子的扩散[2]，得到了广泛应用于蒸散发计算的Penman-Monteith(PM)公式。近年来，许多学者在Penman-Monteith公式的基础上，又开展了不同程度的研究。莫兴国等提出了基于Penman-Monteith公式的双源蒸散发模型[3-4]，将植被冠层和土壤表面作为两个源汇项分别进行计算，从而得到流域蒸散发量。袁飞又对其进行再次改进，将植物生长模型导入双源蒸散发模型作为模型的输入，实现了随植被叶面积指数动态变化的流域蒸散发量的计算[5]。但是目前常用的蒸散发模型均属于单层模型，将整个流域蒸发面考虑成一个整体，忽略了土地利用条件、地貌、植被等的空间差异对蒸散发的影响，在计算下垫面条件复杂的流域蒸散发量时稍有不足[6-7]。

本文基于南阳、枣阳、驻马店、信阳4个气象站及武汉辐射站2010～2018年日观测气象及辐射资料，构建了考虑地形、土地利用及植被叶面积指数的分布式彭曼蒸散发模型及双源蒸散发模型。将构建的模型分别用于计算区域蒸散发能力，并与蒸发皿实测蒸散发能力进行比较，以定量评价不同蒸散发模型在计算湿润地区蒸散发量的适用性。研究成果可为该区域农业灌溉水量预测及分配提供理论依据及技术支撑。

1 研究区概况

选取淮河大坡岭以上流域为研究对象(见图1)，流域位于东经113.273°～113.823°，北纬32.222°～32.713°。控制流域面积为1 631.22 km2，干流长度为73 km。研究区属于湿润地区，流域多年平均降水量939 mm，多年平均径流深为375 mm左右。

图1 研究区域Fig.1 Sketch of study area

2 模型介绍

2.1 植物生长模型

2.1.1植物生长过程

本文采用土壤侵蚀和生产力影响估算(Erosion-Productivity Impact Calculator，EPIC)模型作为植物生长模型。模型假定植物生长是基于每日积累的热量，而温度是表征热量的关键物理量。根据热量理论假定植物生长所需热量可以进行时程分配，当日平均温度大于最低生长温度时，超过部分的热量被植物所吸收，所以需要在植物生长过程中记录每天日平均温度，并将其用热量单位表现出来。当具有种植日期、成熟日期、最低生长温度和日平均气温资料时，即可计算出植物生长成熟所需要的总热量[8-9]。

式(1)可计算植物生长过程中某天所积累的热量单元：

(1)

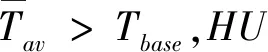
根据式(2)计算植物成熟所需要的总积温：

(2)

式中：PHU是植物成熟需要的总积温，即潜在总积热，℃；m是植物从种植到成熟所经历的天数。

2.1.2叶面积指数计算

叶面积指数(Leaf Area Index，LAI)是指某块土地上植物叶片的总面积与植物占地面积的比值，是影响植物蒸散发的主要因素之一[10-11]，叶面积指数又称叶面积系数。公式如下：

LAI=leafarea/Tarea

(3)

式中：LAI表示植物叶面积指数，m2/m2；leafarea表示植物叶片总面积，m2；Tarea表示植物占地面积，m2。

叶面积指数控制着植物的各种物理、生理过程，例如呼吸作用、光合作用、碳循环、植被蒸腾和降雨截留等，是陆面过程中一个关键的结构参数。

植物生长过程中的潜在积热率可由式(4)进行计算：

(4)

式中：HUi表示截止到第i天植物生长所需要的热量；frPHU表示截止到第d天植物生长的潜在积热率。

2.2 彭曼蒸散发模型

1948年，Penman H L提出了无水汽水平输送情况下的参考蒸发量计算公式，后改进了反映植物气孔几何特性的气孔因子和日照长度因子，改进后的公式可以用于任何低矮绿色作物。同时，Penman又对高大植物引入了改进的风速函数，使Penman公式能够计算高大植物的蒸散发量[12]。得到如下表达式:

(5)

式中：ET0为参照蒸发量，mm/d；Δ为饱和水汽压温度曲线的斜率；γ为湿度计常数，kPa/℃；Rn为净辐射，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；u2为高度为2.0 m处的风速，m/s；es和ea为实际水汽压和饱和水汽压，kPa；λ为水的汽化潜热，MJ/kg。

Monteith J L于1965年在Penman公式的基础上提出了以能量平衡和水汽扩散理论为基础的适用于作物蒸腾量计算的阻力模型，即P-M模型。该模型既考虑了作物的生理特征，又考虑了空气动力学参数的变化，具有较充分的理论依据和较高的计算精度，能比较清楚地反映蒸散变化过程及其影响机制[13-14]，被FAO-56推荐为计算的首选方法。P-M基本方程如下：

(6)

式中：ρa为空气定压密度，kg/m3；cp为空气定压比热，MJ/(kg·℃)；ra为空气动力学阻力，s/m；rs为冠层表面阻力，s/m。

FAO-56按照P-M模型的要求为使其计算标准化，对ET0进行了定义：参照蒸腾量为一种假想的参照作物冠层的蒸腾速率。其假设作物高度为0.12 m，固定的表面阻力为70 s/m，反射率为0.23，其假设条件非常类似于表面开阔，高度一致，生长旺盛，并且完全遮盖地面水分充足的绿色草地的蒸发量。表面阻力主要包括冠层叶面阻力和表层土壤阻力，受气候因素和土壤水分状况的影响随植被种类而变化。

得到的FAO P-M方程为

(7)

式中：T为平均温度，℃。

2.3 双源蒸散发模型

双源蒸散发模型是将土壤表层和植被冠层作为2个相互作用与影响的源汇项，并且互相独立。计算公式如下：

Et=Ei+Epc+Eps

(8)

式中：Et为流域蒸散发能力；Ei为植物冠层实际的截留蒸发量；Epc为植被实际的蒸腾量；Eps为土壤实际的蒸发量。Ei、Epc和Eps的计算公式如下：

(1) 植被冠层截留蒸发Ei(被植被叶面截留的那部分水量的蒸发)。

(9)

(2) 植被蒸腾能力计算(土壤含水量达到田间持水量时，植被叶面气孔所能蒸发的水分)。

(10)

(3) 土壤蒸发能力(土壤含水量到达田间持水量时，裸土或者植物冠层以下土壤所蒸发的水分)。

(11)

式中：Rnc表示植物冠层获取的太阳净辐射值，W/m2；Rns是土壤表面得到的太阳净辐射值，W/m2；G是土壤热通量值，W/m2；ρ是平均空气密度，kg/m3；γ是空气湿度常数值，kPa/℃；Δ是饱和水汽压梯度值，kPa/℃；Cp是空气比热值，1.013×10-3kJ/(kg·℃)；λ是蒸发潜热值，MJ/kg；Wfr是潮湿冠层比例值；γac是植物冠层总的气孔阻抗值，s/m；γcp是土壤表面阻抗值，s/m；γas为植物冠层源汇高度与土壤表层之间的空间动力学阻抗值，s/m；γsp为冠层总的边界层阻抗值，s/m；D0是植物冠层的源汇高程处水汽压强差的值，kPa。

3 结果与分析

3.1 研究资料

选取2010～2018年武汉站的净辐射资料及流域附近的南阳、枣阳、驻马店和信阳4个气象站的日平均气温、日最高气温、日最低气温、日平均水汽压、日照时间及日平均风速等气象资料。流域2010s的土地利用类型由旱地(47.6%)、森林(47.6%)、灌木丛(3.4%)及水田(0.2%)等组成(见图2)。

图2 土地利用组成Fig.2 Composition of land use

3.2 模型计算结果与分析

彭曼蒸散发模型及双源蒸散发模型计算得到的流域日蒸散发能力，及蒸发皿的实测蒸散发能力变化过程如图3所示。

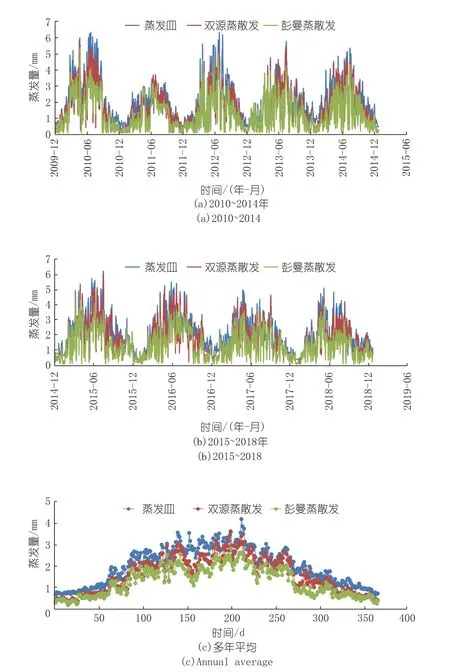
图3 大坡岭流域2010～2018年蒸散发模拟结果Fig.3 Comparisons of simulation results of evapotranspiration at Dapoling basin from 2010 to 2018

由2010～2018年各年及多年平均的日蒸散发能力变化过程可以发现：彭曼蒸散发模型及双源蒸散发模型计算的流域蒸散发能力，与蒸发皿实测的蒸散发能力的变化趋势基本一致。同时可以看出：由于蒸发皿计算的蒸散发能力是水面蒸发，要明显大于模型计算的流域蒸散发能力，蒸发皿的实测值比双源蒸散发模型计算值高126～159 mm，比彭曼蒸散发模型计算值高239～313 mm。

双源蒸散发模型对流域蒸散发能力的计算既考虑植被冠层又考虑土壤表层，而彭曼蒸散发模型只考虑了植被的蒸散发[15-16]，所以双源蒸散发模型计算的蒸散发能力大于彭曼蒸散发模型，年蒸散发能力高于彭曼蒸散发模型113～179 mm。

对日蒸散发能力的变化过程分析发现，3种方法计算的蒸散发能力均是夏季(180～240 d)普遍比其他季节大。主要是因为夏季植物叶面积指数达到最大，且处于汛期，降雨量也偏大，同时温度较高，所以计算得到的蒸散发能力最大。

为进一步比较2个蒸散发模型计算的结果与蒸发皿实测值的相似性，以及2个蒸散发模型在淮河大坡岭以上流域的适用性，本文分别建立了蒸发皿的实测蒸散发量与模型计算的蒸散发能力的线性回归方程，并建立相关关系，对其进行相关关系分析。

双源蒸散发模型和彭曼蒸散发模型计算得到的多年平均日蒸发量与蒸发皿多年平均日蒸发量的相关关系如图4所示。相关系数均大于0.9，均具有较好的相关性。

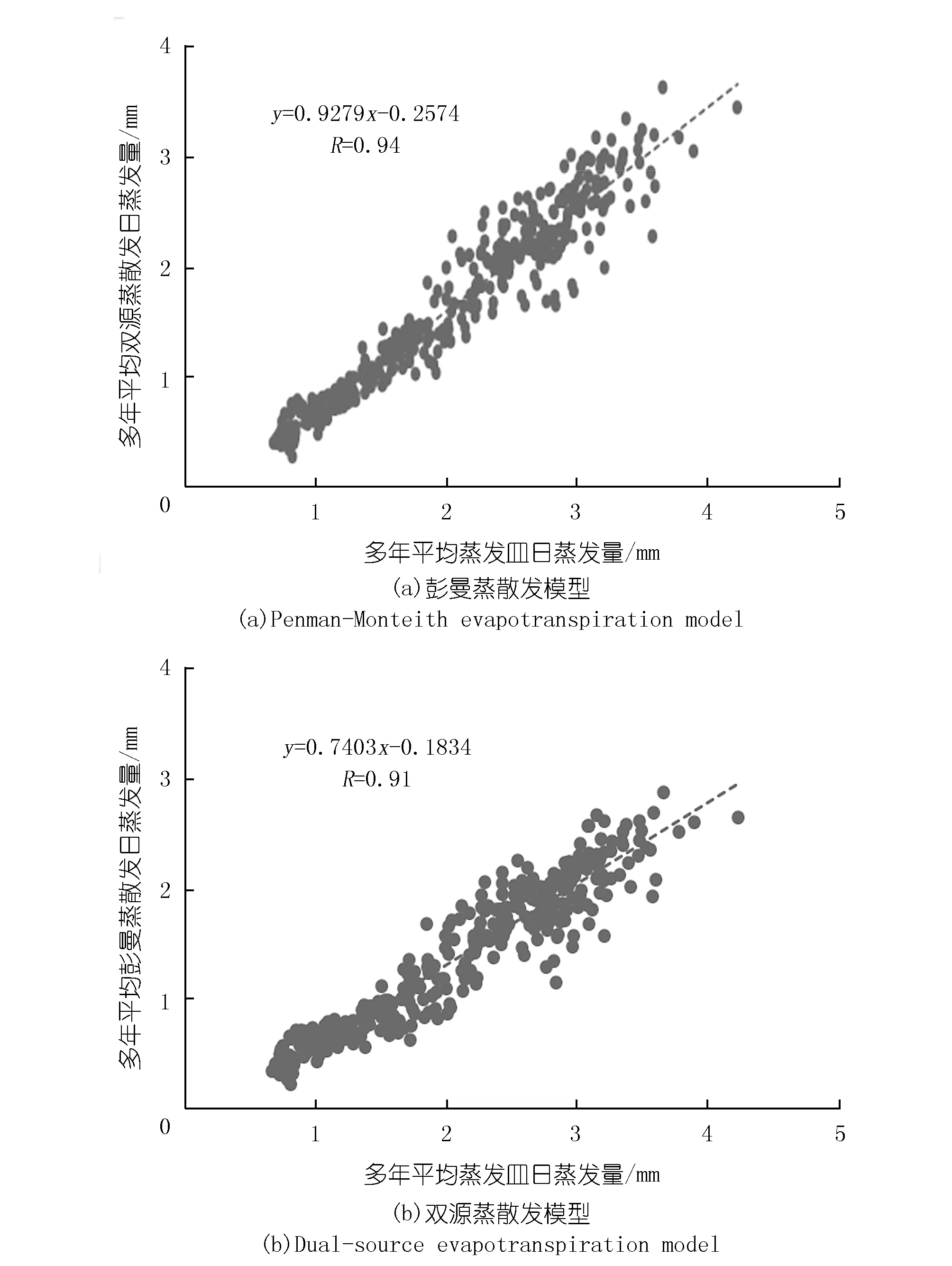
图4 蒸散发能力计算值与实测值相关关系Fig.4 Correlation between evapotranspiration capacity calculated value and measured value

由表1及表2可知：2010～2018年彭曼蒸散发模型计算的蒸散发能力与蒸发皿的实测蒸发值的相关系数为0.80～0.91；双源蒸散发模型计算的蒸散发能力与蒸发皿的实测蒸发值的相关系数为0.84～0.94；且双源蒸散发模型计算的蒸散发能力与蒸发皿实测值之间的相关系数明显好于彭曼蒸散发，更符合实测蒸发量，比彭曼蒸散发模型具有较好的适用性。

表1 彭曼蒸散发模型计算的蒸散发能力与蒸发皿实测值相关系数Tab.1 Correlation coefficients between evapotranspiration capacity calculated by Penman-Monteith evapotranspiration model and measured value of evaporating pan

表2 双源蒸散发模型计算的蒸散发能力与蒸发皿实测值相关系数Tab.2 Correlation coefficients between evapotranspiration capacity calculated by dual-source evapotranspiration model and measured value of evaporating pan

注：多年平均相关系数为0.91。

4 结 论

本文将彭曼蒸散发模型以及双源蒸散发模型与考虑植被叶面积指数的植物生长过程模型耦合，构建了能够反映气象条件、土地利用及土壤特性的时空差异性对流域蒸散发影响的分布式蒸散发模型，并应用于淮河大坡岭以上流域。

(1) 彭曼蒸散发模型和双源蒸散发模型计算得到的流域日蒸散发能力与当地蒸发皿观测资料在时间上具有较好的相似性和一致性。

(2) 考虑植被叶面积指数动态变化的分布式双源蒸散发模型计算的流域蒸散发能力与蒸发皿实测蒸散发的相关关系好于彭曼蒸散发模型，能够较精确地模拟估算湿润地区的蒸散发量。