一种求解FJSP的混合遗传算法

贾培豪,毋 涛

(西安工程大学 计算机科学学院,陕西 西安 710048)

0 引 言

在传统的作业车间调度问题(job-shop scheduling problem,JSP)中,一道工序只存在一台加工机器,但在企业实际车间生产过程中往往会出现并行机器的现象,导致传统的作业车间调度不能很好地满足企业实际需求,由此,柔性作业车间调度问题(flexible job-shop scheduling problem,FJSP)便应运而生[1]。FJSP是JSP的一种扩展,相较于JSP而言更为灵活,在规定工序的同时,还需对每道工序分配加工机器,是复杂的NP问题。正是由于FJSP具有较高的应对复杂性问题的能力和解的灵活性,所以更符合车间生产的实际需求,因此成为了车间调度领域的重点研究方向[2]。

近年来,人们对于此类问题的求解，主要采用智能算法作为解决手段。CHAUDHRY等对1990—2014年期间发表的191篇关于求解柔性作业车间调度问题的论文进行了调查分析,发现34%的论文都是通过遗传算法或混合遗传算法来求解FJSP[3]。由此可知,遗传算法已经是解决FJSP的主流方法,但遗传算法在实际应用过程中往往容易陷入局部最优陷阱[4]。对此,张超勇等针对FJSP问题的特点提出了一种基于双层编码的交叉及变异算子,使得子代能更好地继承父代的优良特征,提高了遗传算法求解FJSP的解的质量[5];ISHIKAWA等提出了一种名为多层次空间竞争性分布式遗传算法(hierarchical multi-space competitive distributed genetic algorithm,HmcDGA)的算法求解FJSP,该算法虽然具有竞争优势,但是计算成本较高[6];LI等提出一种将禁忌搜索算法局部搜索能力强的特点与遗传算法全局搜索能力强的特点有效结合的禁忌混合遗传算法求解FJSP,以此增强遗传算法局部搜索能力[7];杨振泰等改进传统的Powell搜索法,提出了一种融合Powell搜索法的改进遗传算法,改善了遗传算法在进化过程中产生不可行解的情况[8]。

综上所述,改进标准遗传算法亦或通过融合其他算法优化标准遗传算法是求解FJSP的研究趋势。本文提出一种鲸鱼群混合遗传算法。在遗传算法的基础之上,通过将鲸鱼群算法计算出的鲸鱼个体与遗传算法得到的染色体相比较,替换掉原有遗传算法中适应度较低的染色体个体,实现鲸鱼群算法不断向遗传算法输送新鲜血液的目标,以此提高遗传算法求解质量与稳定性。

1 FJSP概述

1.1 问题描述

假设生产车间有待加工工件{J1，J2，…，Jn},有可用机器{M1,M2,…,Mm},其中每个工件包含多道加工工序,每道工序存在至少一台机器可供加工选择,且不同机器加工同一工件的耗时也不尽相同。因此,任一工件选择不同机器进行加工所得到的调度总时长也会有所不同。那么，如何为工件合理的指派加工机器，从而使得加工总时长最短即为问题的求解目标。

1.2 数学模型

柔性作业车间调度问题需满足如下约束:

1) 工件加工工艺锁定,即每个工件加工的顺序不得改变,前一道工序的加工必须在后一道工序加工开始之前完成;

2) 在任何一个时间节点上,一台机器只允许加工一个工件;

3) 同一时刻,同一工件的同一道工序只能被一台机器所加工;

4) 加工过程视作一种理想化的情景,即不考虑外部环境的影响,且加工一旦开始便不可中断;

5) 所有的工件都须在0时刻开始加工。

结合文献[9],现给出柔性作业车间调度问题的数学模型。为了方便介绍,首先定义说明相关的数学符号,如表1所示。

问题的优化目标为“最大完工时间”,即工件生产调度所需的最大完工时间最小,目标函数(Fg)为

Fg=min max(Cj),1≤j≤n

(1)

式(1)拥有如下约束:

Sjh+Pijh≤Skl+α(1-yijhkl)

(2)

式中：j=0,1,…,n;k=1,2,…,n;h=1,2,…,hj;l=1,2,…,hk;i=1,2,…,m。

Cjh≤Sj(h+1)+α(1-yiklj(h+1))

(3)

式中：j=1,2,…,n;k=0,1,…,n;h=1,2,…,hj-1;l=1,2,…,hk;i=1,2,…,m。

表 1 数学符号及其定义Tab.1 Mathematical symbols and definitions

Cmax≥Cjhj,j=1,2,…,n

(4)

Sjh+xijhPijh≤Cjh。i=1,2,…,m;

j=1,2,…,n;h=1,2,…,hj

(5)

Cjh≤Sj(h+1)。j=1,2,…,n;

h=1,2,…hj-1

(6)

(7)

Sjh≥0,Cjh≥0

(8)

式(2)和式(3)表示了在任何1个时间节点上,1台机器只允许加工1个工件;式(4)、式(5)和式(6)表示了加工的总时间大于任意工件完工时间且每个工件加工的顺序不得改变,前一道工序的加工必须在后一道工序加工开始之前完成;式(7)表示任何1个工件的任意一道工序都只能选择1台机器进行加工;式(8)表示所有的工件都需要在0时刻才能开始加工。

2 算法设计

2.1 遗传算法

2.1.1 染色体编码 采用双层编码方式进行染色体编码工作,即对工序以及机器指派分别编码[10]。第一层为工序编码。首先构造数列S,假设有Ji个工件需要加工,那么每一个工件均包含PJi道工序。数列S的长度为l,且l=PJ1+PJ2+…+PJi；数列S的基因S[t]∈[1,l],且S[t]不重复。与此同时,再构造数列C,数列C包含PJ1个1,PJ2个2,PJ3个3,以此类推得出数列C。根据数列S对数列C重排序,得到一个新的数列SC，即为工序编码。第二层为机器指派编码。同样构造一个数列M,数列M的长度与数列SC长度相同,数列M的基因为与之索引相对应的工序加工采用第几个可用机器。

例如,有2个工件J1和J2需要加工,共有3台机器可供选择,其中J1包含2道工序,J2包含4道工序,那么PJ1=2,PJ2=4,l=PJ1+PJ2=6。有3台机器可供选择且M的长度等于6,则该问题下一个合格的染色体可以表示为“3,4,1,5,2,6,1,2,2,1,2,3”,其中数列S={3,4,1,5,2,6},生成的数列C={1,1,2,2,2,2}。根据数列S对数列C进行重排序得到数列SC={2,2,1,2,1,2},其中数列SC中索引为0的数字2表示零件2的第1道加工工序,索引为1的2表示零件2的第2道加工工序,以此类推。数列M={1,2,2,1,2,3},其中索引为0的数字1表示零件1的第1道加工工序选用它可用机器的第1个进行加工,索引为1的数字2表示零件1的第2道加工工序选用它可用机器的第2个进行加工,以此类推。

2.1.2 适应度函数 优化目标为“最大完工时间”,即完成加工所需的总时间越短则个体适应度越好,适应度函数Ff表示为目标函数的倒数形式,即

Ff=1/Fg

(9)

2.1.3 选择操作 选用轮盘赌选择法[11],即种群N中个体i的适应度为Fi,则个体被选择遗传到子代的概率为

(10)

从式(10)可以看出,个体选中的概率与适应度函数成正比。

2.1.4 交叉操作 对双层遗传算子均采用两点交叉的方式进行。即随机选择2个染色体作为父代染色体,并在染色体长度范围之内随机产生2个大于等于0的数字作为索引,然后交换2个索引之间的基因片段,随即得到2个子代染色体;判断得到的子代染色体是否符合编码规范,若不符合则需对其进行修补,修补方式为取交叉片段的补集随机重排列到非交叉片段。例如,产生随机数rand(1)=1,rand(2)=3,若2条父代染色体分别为“1,3,2,5,4,6”和“1,2,4,5,3,6”,则交叉片段为索引1到索引3的值,即“3,2,5”和“2,4,5”；进行基因片段互换,得到两条子代染色体为“1,2,4,5,4,6”和“1,3,2,5,3,6”。可以看出，染色体交叉后不符合规范,因此对其进行修补。按照上述方法修补后的两条染色体分别为“1,2,4,5,3,6”和“1,3,2,5,4,6”,至此完成交叉操作。

2.1.5 变异操作 由于文中采用双层编码的方式,因此染色体变异操作也是分双层进行。对于第一层遗传算子的变异操作采用两点变异,即在染色体长度范围之内随机产生2个大于等于0的数字作为索引,然后交换这2个索引所对应的基因的值。例 如,产生随机数rand(1)=2,rand(2)=3,一条染色体为“1,3,4,6,5,2”,则交换索引为2和索引为3的值,即得到新的染色体“1,3,6,4,5,2”。对于第2层遗传算子的变异操作则采用单点变异,即同样产生一个随机数作为索引,然后对该索引所对应的基因进行变异,变异范围为该道工序可用机器数。例如,产生随机数rand(1)=1，一个染色体为“1,2,2,1,2,3”,则变异后的染色体为“1,3,2,1,2,3”。

2.2 鲸鱼群算法部分

2.2.1 算法概述 鲸鱼群算法(whale swarm optimization algorithm,WSA)是2017年诞生的一种新型启发式算法,由华中科技大学的ZENG等受鲸鱼通过声音交流寻找猎物的行为启发所提出[12]。所有的鲸鱼都通过超声波进行交流,不同距离的超声波强度(ρ)[13]为

ρ=ρ0exp(-ηd)

(11)

式中：d为距离；η是超声波传播的衰减系数；ρ0为超声波强度。当η不变时,ρ随着d的增加呈现下降趋势,即随着距离的增大,超声波的强度会降低。当2条鲸鱼间距离较远时,无法确定所发出的猎物信息是否正确,因此鲸鱼总是会积极地向着“较好且最近的”鲸鱼移动,反之亦然。正是因为每条鲸鱼都是向着“较好且最近的”鲸鱼进行移动,在经过一段时间鲸鱼的运动后,就会产生一些鲸鱼群。受这种鲸鱼寻找食物的启发,文献[12]建立了如下算法迭代方程，即

(12)

2.2.2 鲸鱼个体距离 鲸鱼群算法编码方式同样是采用基于机器和工序的双层编码方式。但是,由于鲸鱼群算法在提出时是用于解决连续性问题的,而基于双层编码求解FJSP属于离散问题,所以导致鲸鱼个体间距离计算方式以及鲸鱼移动规则均无法直接使用。由此,本文引入文献[14]所提出的鲸鱼个体距离计算方法及移动规则,以2.1.1节中的编码为例进行说明。一个完整的编码为{1,2,2,1,2,3,2,2,1,2,1,2},若Pos表示鲸鱼个体在解空间的位置，则基于Pos向量的鲸鱼个体表示如图1所示。

图 1 鲸鱼个体表示Fig.1 Individual whale representation

由图1可得,由机器编码得到Pos中的机器号,由工序编码在对应机器上的加工顺序得到Pos中的Seq值，其中Seq表示工序在所选机器上的加工次序。机器号和Seq值等2部分共同组成了Pos向量,即鲸鱼个体在解空间当中的位置表示。用Pos向量表示法计算鲸鱼个体间距离(Dis),即

(13)

2.2.3 鲸鱼个体移动 计算出鲸鱼个体间距离后,由“最优且最近”的引导鲸鱼引导其移动。鲸鱼个体移动步骤如下:

1) 以总工序数作为长度,随机生成一组由0和1组成的数组;

2) 保留数组中1所对应的鲸鱼个体工序及机器编码,复制到新鲸鱼个体中;

3) 对数组中0所对应的工序建立集合,在引导鲸鱼个体中寻找集合中对应工序以及机器编码,将其按照引导鲸鱼个体中的顺序依次填充新鲸鱼个体中的空缺部分。

完成鲸鱼个体的移动之后，形成新的鲸鱼个体。鲸鱼个体移动规则如图2所示。

图 2 鲸鱼个体移动规则Fig.2 Movement rules of individual whale

将移动后得到的鲸鱼个体与遗传算法得到的染色体相比较,替换掉原有遗传算法中适应度较低的染色体个体,实现鲸鱼群算法不断向遗传算法输送新鲜血液的目标。

2.3 鲸鱼群混合遗传算法执行流程

所提出的鲸鱼群混合遗传算法(WSA-GA)是在遗传算法的基础之上,通过将鲸鱼群算法计算出的鲸鱼个体与遗传算法得到的染色体进行重组,从而改进了遗传算法。鲸鱼群混合遗传算法执行流程如图3所示。

图 3 鲸鱼群混合遗传算法流程图Fig.3 Flow chart of whale swarm hybrid genetic algorithm

3 实验与结果分析

3.1 环境与算法参数

实验环境为Window 10系统,内存16 G,处理器四核I5-7300HQ 2.5 GHz,实验工具为MatlabR2016a。算法参数设置如下:种群规模=200,算法迭代次数=200,变异概率pm=0.1,交叉概率pc=0.7。

3.2 算例验证

为了验证WSA-GA算法的有效性,通过Kacem基准算例[15-16]对算法进行验证。对4×5,8×8,10×7,10×10以及15×10等5种规模的算例分别进行仿真实验,将5种算例分别执行20次,记录最优结果以及20次实验结果平均值。将本文所提出的WSA-GA算法与文献[17-22]中的算法结果相对比,并对比传统遗传求解结果,对比结果如表2所示。

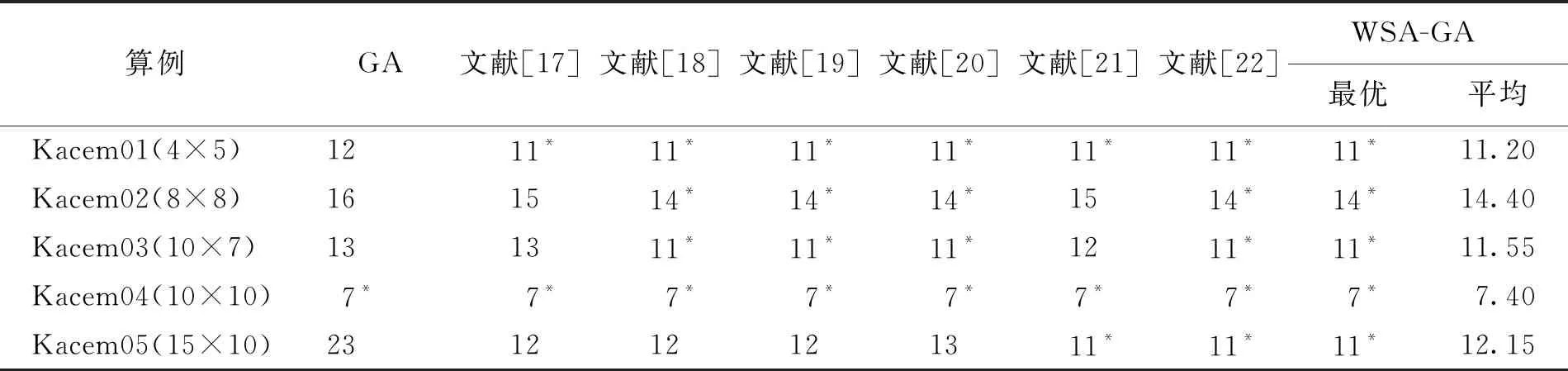
表 2 Kacem算例对比结果Tab.2 Results of Kacem example comparison

选取Kacem 8×8和15×10等2种规模算例,将鲸鱼群混合遗传算法调度结果通过甘特图进行展示,如图4、图5所示。

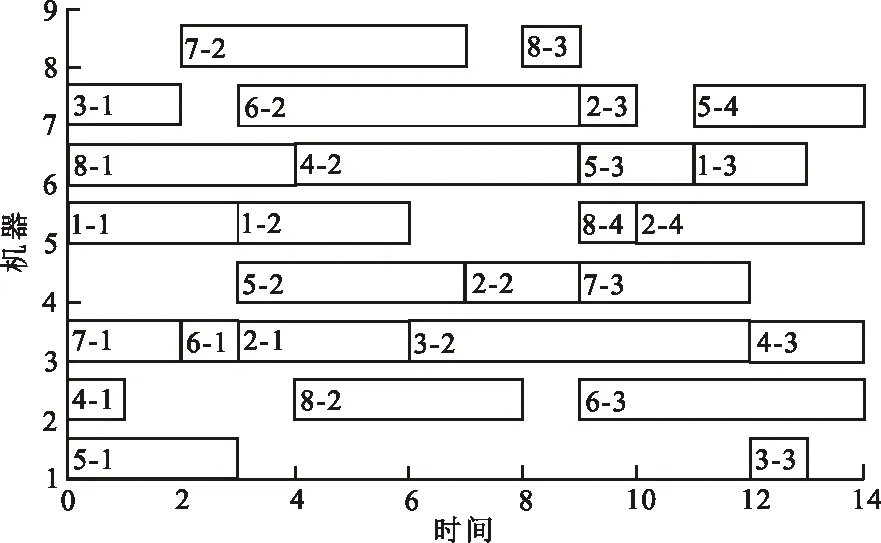
图 4 Kacem 8×8算例调度结果甘特图Fig.4 Gantt chart of Kacem 8×8 example scheduling result

图 5 Kacem 15×10算例调度结果甘特图Fig.5 Gantt chart of Kacem 15×10 example scheduling result

本算法旨在用于实际工业生产,因此求解稳定性与最优结果为算法主要目标。由表2可以看出,所提出的WSA-GA算法在对Kacem 5种规模算例的验证中均能获得最优值且结果较为稳定,相较于传统遗传算法求解结果均有了明显提升,一定程度上验证了算法的有效性与可行性。

4 结 语

针对遗传算法求解FJSP容易陷入局部最优陷阱的问题,提出了一种鲸鱼群混合遗传算法。通过将鲸鱼群算法的鲸鱼个体与遗传算法的染色体进行编码重组,有效地解决了遗传算法“早熟”的问题。仿真实验证明了WSA-GA算法求解FJSP的有效性与可行性,对于解决实际生产调度问题具有一定价值。本文所研究的是单目标的FJSP问题,后续将考虑利用鲸鱼群混合遗传算法解决多目标FJSP问题。