基于新型烟花算法的机器人时间最优轨迹规划
2020-10-28王文杰王晓华
陶 庆,王文杰,王晓华,张 蕾
(西安工程大学 电子信息学院,陕西 西安 710048)
0 引 言
轨迹规划是机器人运动控制的基础,随着智能算法的出现,轨迹规划算法也在向智能化发展,高性能的轨迹规划算法可以使机器人运行更平稳,控制精度更高,工作效率更高,使用寿命更长,因此对轨迹规划算法的研究一直是机器人领域的研究热点。
三次多项式插值轨迹规划[1]计算简单,应用广泛,但是轨迹规划过程中可能会产生机械振动,增加关节磨损,影响控制精度。为得到更平滑的运动轨迹,采用提高多项式的插值阶次或者进行分段插值的方法,文献[2]提出了采用 3-5-3 样条函数法对机器人轨迹进行规划,使运动轨迹更加平稳,但是以上方法没有考虑到插值时间问题。机器人时间最优轨迹规划就是要求机器人在多约束条件下,能够以最短的时间完成指定的运动。基于多项式插值的轨迹规划,具有阶次高、没有凸包性质等特点,很难用传统方法优化[3]。使用智能算法实现轨迹规划时间最优成为研究重点,常用的智能算法有人工鱼群算法[4]、差分进化算法[5]、遗传算法[6-8]、粒子群算法[9]、凸优化算法[10],但是这些算法需要的迭代次数较多,参数调整复杂,性能方面有待提高。
烟花算法(fireworks algorithm,FWA)是TAN等在2010 年提出的一种新颖的智能优化算法[11],具有所需参数少,求解性能强等特点。学者们在其基础上进行深入研究并将其应用到各个领域。文献[12]提出增强烟花算法(EFWA),在烟花算法基础上增加最小爆炸半径检测策略,并对高斯变异、映射规则、选择策略进行改进,降低了算法运行时间。文献[13]提出自适应烟花算法(AFWA),无需人为设定最小半径,而是最优烟花自动调整爆炸半径,使算法更加智能。文献[14]提出反向烟花算法,在增强烟花算法中引入反向学习算子,提高了算法求解精度。文献[15]提出精英导向烟花算法(ELFWA),增加了烟花之间的信息交流,较差火花接受随机选择的精英烟花的指导,提高了搜索效率。文献[16] 提出了一种简化的混合烟花算法(SHFWA),通过改变烟花爆炸产生火花的方式,从而化简算法过程,使算法性能提高。但是这些算法依然存在收敛速度较慢等缺陷。
在轨迹规划中,XIA等提出用分段连续函数对轨迹规划过程中的速度和加速度进行限制[17],达到缩短运行时间的目的,但是其运算复杂,计算量较大。HE等采用免疫算法对机器人时间和能量进行同时优化[18],并取得了很好的效果,但是同时优化多个目标,可能会导致时间不是最优的情况。CHEN等采用和声搜索算法对五次B样条曲线进行优化[19],得到了平滑且时间最优的轨迹,而对比分段多项式插值函数,轨迹还不够平滑。
针对以上方法的问题,本文提出了混沌自适应烟花算法,以自适应烟花算法为基础,将混沌算法与其相结合,加速收敛过程,提高求解精度。通过8个不同的测试函数验证了算法的正确性。以UR机器人为研究对象,以在速度约束下插值时间为优化目标,采用混沌自适应烟花算法确定出机器人运动时间最短的轨迹,在满足位置、速度、加速度等一系列约束的情况下,实现速度约束下的时间最优3-5-3多项式插值轨迹规划,解决了时间不确定性问题,证明了算法的正确性。
1 多项式插值函数的构造
为了完成机器人在关节空间中的指定运动,利用已知的笛卡尔坐标系下的起始点、抬起点、下降点和终点的位姿,通过运动学逆解求解出关节角度,从而得到多项式插值函数,使机器人末端经过要求路径点,满足运动轨迹要求。本文采用3-5-3多项式插值方法,其通式如下所示:
(1)
式中:aimn为第i个关节插值轨迹的第m段(m=1,2,3)多项式轨迹函数的第n个未知系数;him(t)为第i个关节的第m段多项式轨迹函数;t为时间变量。
在轨迹规划过程中,需要满足起始点θi1、抬起点θi2、下降点θi3、终点θi4的位置、速度和加速度约束,其约束条件是:4个插值点的位置(已知),起始点的速度与加速度为0,终点的速度与加速度也为0,抬起点的速度和加速度连续,下降点的速度和加速度也连续,通过以上14个约束条件,可以根据式(2)~(4)推导出未知系数aimn。其中式(2)为关于第i个关节的三段插值时间ti1、ti2、ti3的矩阵,式(3)为第i个关节角的位置矩阵,式(4)为系数矩阵。

(2)
式中:A、B、C、D、E、F、G、H的具体内容见文献[3]。
θ=[0 0 0 0 0 0θi30 0θi00 0θi2θi1]T
(3)
a=T-1·θ=[a1a2a3]T
(4)
式中:a1=[ai13ai12ai11ai10];
a2=[ai25ai24ai23ai22ai21ai20];
a3=[ai33ai32ai31ai30]
2 基于CAFWA的时间最优求解
2.1 自适应烟花算法
烟花算法的灵感来源于烟花在燃放过程中会爆炸并且在一定范围内产生火花的行为,是一种群体智能优化算法。烟花算法的步骤大致如下:
初始化即在求解空间产生N个位置任意的烟花,然后爆炸算子在爆炸范围Ai中产生Si个新的火花,其中Ai和Si分别为
(5)

(6)
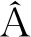
为避免火花数量不均影响性能,将Si改为
(7)
式中:r(·)为取整函数;a和b为给定常数。
为增加火花多样性,对火花采取位移操作和高斯变异:
(8)

(9)

为避免火花位置越过边界,采用映射规则:
(10)

选择策略采用精英保留策略,直接保留适应度最好的火花,采用轮盘赌的方式筛选剩余火花,每个火花被选中的概率为
(11)
式中:R(xi)为个体xi与其他火花的距离之和;K为产生的火花总数。
但是烟花算法具有一定缺陷,若优化函数的最优解位于原点,烟花算法存在“早熟”现象。若优化函数的最优解距原点位置较远,烟花算法性能较差,烟花算法耗时严重。自适应烟花算法是对烟花算法的改进。自适应烟花算法使爆炸半径具有自动调节的能力,对高斯变异,映射规则和选择策略都进行了改进,提高了算法的性能。
选择一个条件满足自适应半径的计算:① 适应度值比这一代的烟花要差;② 到最优个体的距离是满足① 中的个体中最短的个体,将这个个体与最优烟花的距离作为下一次的爆炸半径。初始化半径为整个求解范围。
新型高斯变异算子:高斯火花的计算公式为

(12)

新型映射规则:采用随机映射规则,计算公式为
(13)
式中:U(0,1)为[0,1]区间上的均匀分布随机数。
精英-随机选择策略:首先选择出种群中适应度最优的个体,然后对其余烟花的选择采用随机策略,降低其运算时间。
2.2 混沌自适应烟花算法
混沌搜索的遍历性、随机性有利于智能算法摆脱局部最优值的束缚[20]。很多模型都能产生混沌序列,本文采用逻辑自映射函数产生混沌序列,其数学表达式为
yi+1=1-2×(yi)2,yi∈(-1,1)
(14)
当yi≠0和yi≠0.5时就会有混沌发生。
混沌算法首先将解空间中烟花个体xi的每一维的位置映射到混沌区域(-1,1),映射规则为
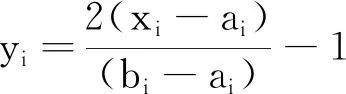
(15)
式中:ai为混沌搜索范围的下边界;bi为混沌搜索范围的上边界。
然后对式(15)中映射产生的值,按照式(14)进行迭代,生成混沌序列。最后混沌序列逆映射,将混沌区域的值逆映射到解空间。逆映射规则为
(16)
CAFWA的步骤:
1) 初始化算法基本参数,包括烟花种群数、爆炸火花数、高斯火花数、优化范围等。
2) 根据混沌算法对随机产生的N个烟花进行优化,选择其中最好的N个烟花作为初始烟花。
3) 计算初始烟花的适应度。
4) 计算最优烟花除外的各个烟花的爆炸半径及所有烟花的爆炸数目。
5) 产生成高斯火花。
6) 计算所有火花的适应度值。
7) 计算最优烟花半径。
8) 选择下一代烟花。
9) 用混沌算法对产生的烟花进行优化,更新种群。
10) 如果未达到最大迭代次数,则执行步骤4)。
11) 输出最优烟花及其适应度值。
2.3 算法测试
为测试CAFWA算法的性能,选择烟花算法(FWA)和自适应烟花算法(AFWA)进行对比,测试函数如表1所示,其中f1和f2为只有一个极值点的单峰函数,f3~f5为拥有多个极值点的多峰函数,f6~f8为多峰函数且最优解的位置不在原点附近,能够比较全面的评估算法的性能。
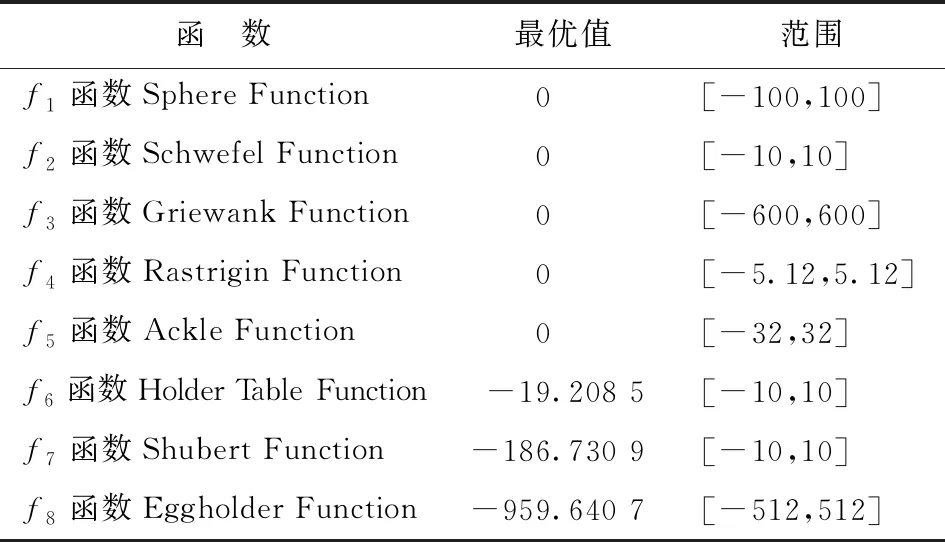
表 1 测试函数Tab.1 Test functions
测试函数时各算法的参数统一,其中最大迭代次数为10 000,烟花数目为5,火花数目为50,测试维度为10。每种算法独立重复运行50次,把最佳适应度值对应的平均值、方差和运行时间作为算法性能的评价标准,测试结果如表2所示。
根据表2可以看出,在求解前5个函数时烟花算法具有很好的效果,这是由于烟花算法不够完善造成的,而且其算法耗时严重。而AFWA和CAFWA相比,CAFWA对单峰函数求解结果相差不大,但是对于多峰函数具有更高的求解精度,而且时间和AFWA相差不多且远远小于FWA算法。
2.4 适应度函数的选择
若选择未知系数aimn为待优化的目标函数,则混沌自适应烟花算法优化的维数为14,增加了寻优的困难程度。以第i个关节的三段插值时间ti1、ti2、ti3为目标函数,使搜索维度大大降低,运算更加简单。待优化的目标函数是使各关节在速度的约束下运行时间最短,其目标函数为
f(t)=min(ti1+ti2+ti3)
(17)
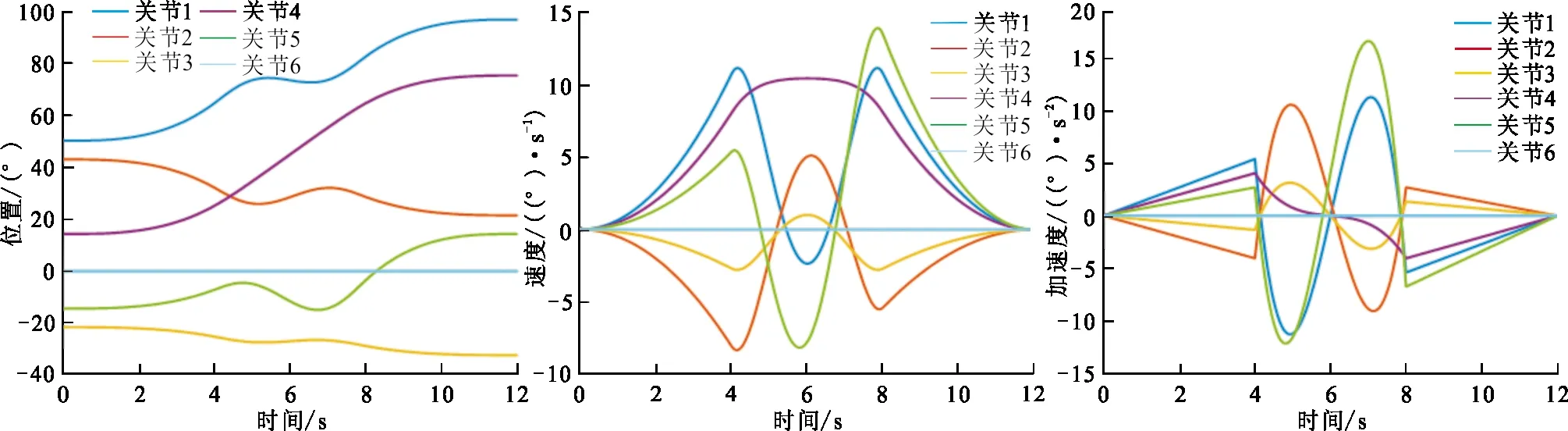
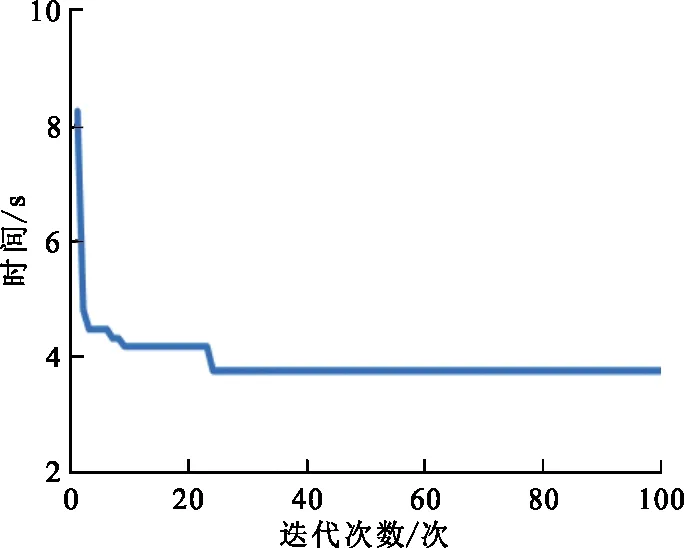
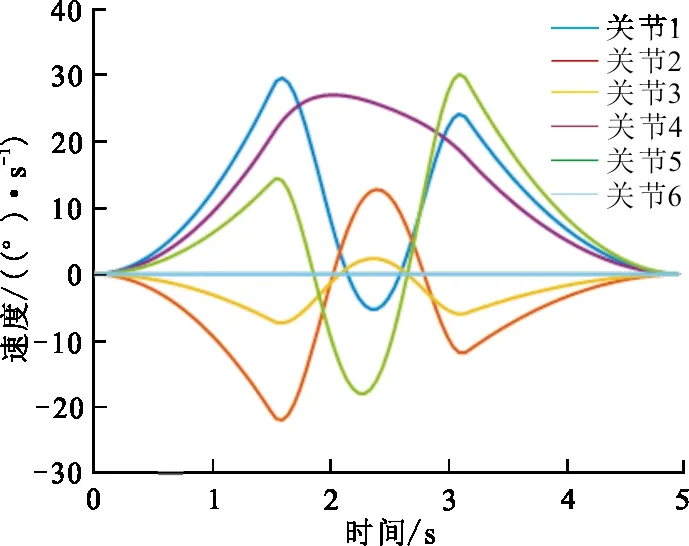
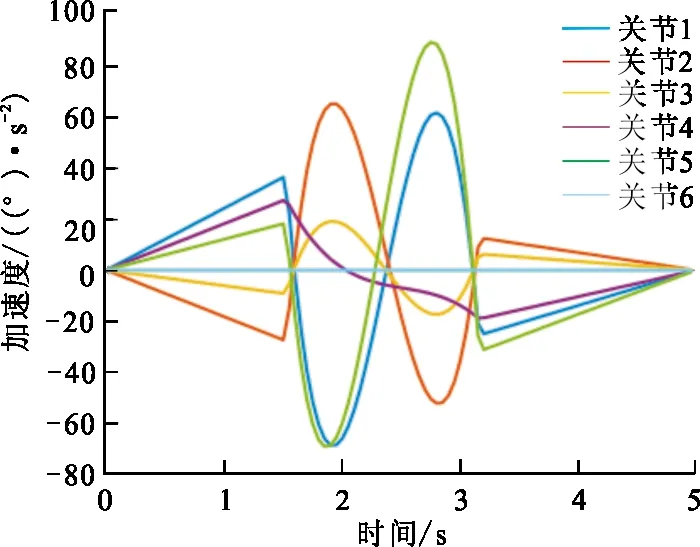
max{vi} (18) 式中:vi为各段多项式的实时速度;vimax为关节的限制速度。 表 2 测试结果Tab.2 The test results 基于混沌自适应烟花算法的机器人时间最优轨迹规划算法就是以关节速度为约束条件,选择最短的关节运动时间。 本文以UR机器人为例,采用旋量理论对其进行运动学建模,如图1所示,其中各旋转轴方向的单位矢量ωi,位置矢量ri等参数见表3。 图 1 UR机器人结构图Fig.1 Structure diagram of UR robot 表 3 UR机器人参数 根据Paden-Kahan子问题法和消元法对UR机器人进行逆运动学分析,将笛卡尔空间坐标系下的插值点变成关节空间的角度插值点。给定机器人末端的位姿信息,如表4所示。表4中路径点前3个值为位置信息,后3个值为姿态信息。根据其位姿信息可以求解出各关节在各路径点时所对应的角度,如表5所示。 表 4 机器人末端的位姿信息Tab.4 Posture information at the end of the robot 表 5 关节角度插值点 传统的3-5-3多项式插值方法,各段插值时间是人为给定的具有不确定性,从而影响机器人的工作效率,图2是给定各段插值时间为4 s时各关节运动的位置、速度、加速度曲线。 (a) 位置变化曲线 (b) 速度变化曲线 (c)加速度变化曲线图 2 3-5-3多项式插值的关节位置、速度、加速度变化曲线Fig.2 3-5-3 polynomial interpolation curve of joint position, velocity and acceleration 根据图2可知其满足起始点和终点的速度与加速度都为0,抬起点和下降点的速度和加速度连续的约束条件,综合考虑安全、稳定、效率等多方面因素,UR机器人各关节的速度最大为30°/s,但是由图2(b)可以发现机器人各关节的最大速度还未能到达所允许的最大速度,这就导致其工作效率不高。 采用混沌自适应烟花算法对有速度约束的3-5-3插值多项式方法求解最优时间。以求解关节1的最优时间为例,本文设定初始烟花数目N为5,在三维解空间内进行最优化搜索,初始的烟花位置为[0.01,4]的任意随机数,烟花爆炸产生火花m的数目为50,循环迭代100次。可以得到最优粒子进化图,如图3和图4所示。 图 3 关节1的最优时间粒子进化图Fig.3 Optimal time particle evolution diagram of joint 1 图 4 关节1的总时间最优粒子进化图Fig.4 Total time optimal particle evolution diagram of joint 1 同理可以得到其他关节的各段最优时间,如表6所示。 表 6 各关节最优时间 Tab.6 Optimal time of each joint 单位:s 关节iti1ti2ti3 11.524 50.779 91.498 6 21.138 00.186 60.709 2 30.369 30.148 90.357 9 41.197 41.634 41.195 3 50.756 90.207 81.838 6 60 0 0 由于机器人的关节运动具有时间同步性,所以选择每段插值时间里的最大值max(ti1)=1.524 5 s,max(ti2)=1.634 4 s,max(ti3)=1.838 6 s作为每段的插值时间。与未经优化的3-5-3插值多项式插值时间相比减少了7.002 5 s。 图5是采用混沌自适应烟花算法得到最优插值时间后,机器人的位置、速度、加速度曲线。由图5可知,优化后也满足起始点和终点的速度与加速度都为0,抬起点和下降点的速度和加速度连续的约束条件。对比未经优化和优化后的位置曲线可以发现时间缩短后其位置变化和未优化时相差不大。对比速度曲线可以发现优化后各关节速度都有所增加,但都未超过限制速度,且最大速度趋近于限制速度,这样能够在保障安全的情况下提高工作效率,验证了算法的正确性。 (a) 位置变化曲线 (b) 速度变化曲线 (c) 加速度变化曲线图 5 优化后关节位置、速度、加速度变化曲线Fig.5 The curve of joint position,velocity and acceleration after optimization 本文提出了一种混沌自适应烟花算法,针对自适应烟花算法收敛速度慢、精度低等缺陷,将混沌算法与自适应烟花算法相结合,将随机初始化改为混沌初始化,在选择策略之后进行混沌优化,提高其收敛速度和求解精度,对8个测试函数进行测试,可以发现,CAFWA在求解多峰函数和最优解距离原点较远的问题时具有更好的性能。 以UR机器人为例,在关节空间中,以速度为约束条件,提出了基于混沌自适应烟花算法的时间最优轨迹规划方法。由于传统 3-5-3 多项式插值,各段插值时间具有不确定性,所以对机器人的工作效率,机械磨损及生产安全会产生不利的影响。通过Matlab仿真可以发现经过混沌自适应烟花算法优化后,机器人各关节平稳运行且各关节都满足速度约束,其速度、加速度在插值时间点连续且平滑,该算法有较高的实用价值。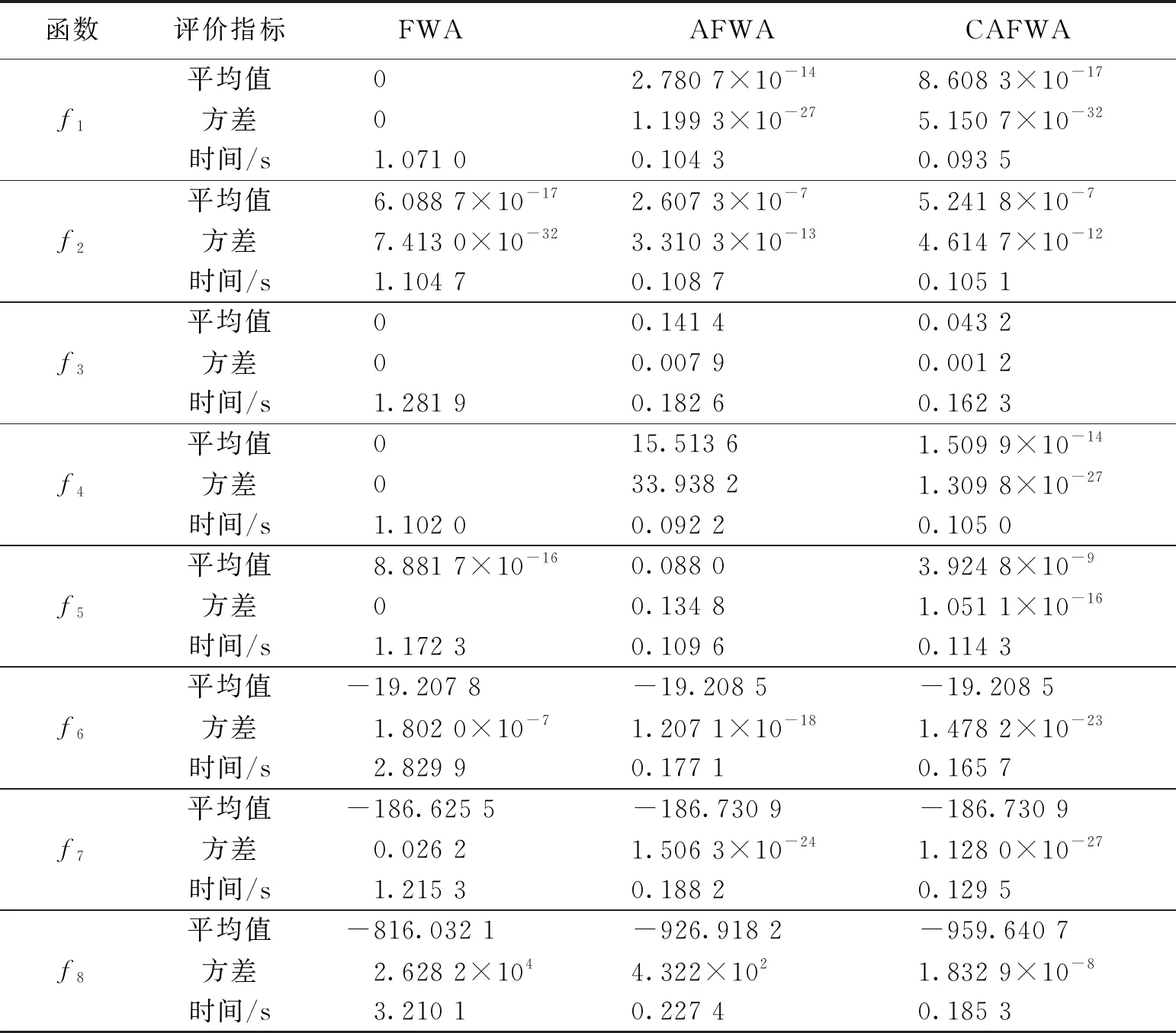
3 仿真结果验证及分析







4 结 语
