投影寻踪分类模型在常见造纸纤维原料综合评价中的应用

赵静远 熊智新，* 梁 龙 房桂干

（1.南京林业大学江苏省制浆造纸科学与技术重点实验室，江苏南京，210037；2.中国林业科学研究院林产化学工业研究所，江苏南京，210042）

对于不同种类的造纸纤维原料，采用的制浆造纸工艺以及生产的纸浆性能也不同，主要原因是造纸纤维原料中的纤维素、半纤维素、木质素、抽提物和灰分等组分的含量差异。造纸纤维原料的分类不仅包括植物分类学，还应该与其独有的纤维特性及其制浆工艺联系起来［1］，合理地对造纸纤维原料进行分类，有利于正确评价它们的制浆性能并制定相应的制浆工艺条件。

在制浆生产和科研实践中，已经积累了大量有关造纸纤维原料的材性资料。同时，通过以近红外光谱（Near Infrared Spectroscopy，NIRS）为代表的过程分析技术（Process Analytical Technology，PAT）也可以快速获取大量的造纸纤维原料化学组分［2-4］的数据。因此，有必要以这些数据为基础，研究如何采用现代数据分析手段对造纸纤维原料进行及时、客观、合理的评价，进而指导生产和管理，这将有利于进一步提高制浆造纸工业的自动化和智能化水平。在造纸纤维原料综合评价方面，吴新生等［1］运用主成分分析法对造纸纤维原料进行了有效分类；任建中等［5］利用主成分分析法，对杨树无性系进行优良无性系多性状选择，并作为无性系选择的参考。但主成分分析法存在一定的缺陷［6］，虽然该方法对大量的高维数据指标进行了有效降维处理，也克服了评价指标之间存在的相关性问题，但若评价指标体系中存在一部分变量高度相关，而其他变量低度相关时，则可能会导致不重要指标间的信息重叠强化，使得评价结果无法真实地反映实际情况，并且运用主成分分析法得到对应的主成分含义不明确［7］。

针对主成分分析法在综合评价中的不足之处，本研究采用基于实数编码的加速遗传算法（Real-coded Accelerating Genetic Algorithm，RAGA）与投影寻踪分类（Projection Pursuit Classification，PPC）模型相结合的方法，构建了RAGA-PPC模型，并对我国常用造纸纤维原料进行有效的分类和综合评价。PPC模型能有效排除与数据结构特征及特征关系很小的变量间的干扰，找到样本数据间的内在联系，可以满足高维非正态数据分析的需要，现已被广泛应用于水利［8-11］、农业［12-13］、土木工程［14］、林业［15］、轻工业［16］等行业。利用RAGA-PPC模型不仅可以有效计算出投影值的大小并对造纸纤维原料进行分类，还可以通过最佳投影方向找出对造纸纤维原料分类影响最大的因素。

1 算法模型

1.1 PPC模型

PPC模型的基本思想［17］是将多组高维数据通过降维的方法，投影到低维的子空间上，找出能反映高维数据结构或特征的投影值，然后通过投影值的大小及投影方向来分析高维数据的具体结构特征。PPC模型的建模过程包括以下3个步骤。

（1）样本评价指标的归一化处理。设每个指标值的样本集为｛x*（i，j）|i=1，2，…，n；j=1，2，…，p｝，其中x*（i，j）表示第i个样本中的第j个评价指标，n和p分别表示样本的个数和评价指标的个数。为了消除各样本指标值的量纲差异和统一各样本评价指标值的变化范围，采用下式进行极值的归一化处理：

其中，xmax(j)和xmin(j)分别为第j个指标值的最大值和最小值，x(i，j)为指标特征值的归一化序列。本文研究仅分类而不进行优选排序，为简化计算以提高方法的通用性，指标都按式（1）进行归一化处理。

（2）构造投影指标函数Q（a）。将p维数据｛x（i，j）|j=1，2，…，p｝综合成以a=｛a（1），a（2），a（3），…，a（p）｝为投影方向的一维投影值z（i）：

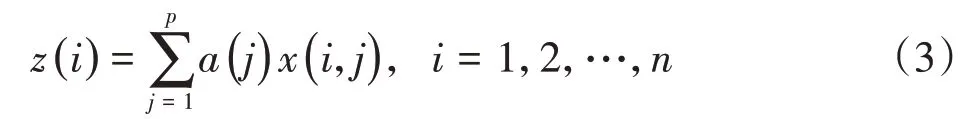
然后再根据｛z（i）|i=1，2，…，n｝的一维散布图进行分类。在综合投影指标值时，要求投影值的散布特征应为：局部的投影点应尽可能密集，最好凝聚成若干个点团，而在整体的投影上要求投影点团之间尽可能散开。投影指标的函数可以表示为：

其中，Sz为投影值的标准差，Dz为投影值的局部密度，即：

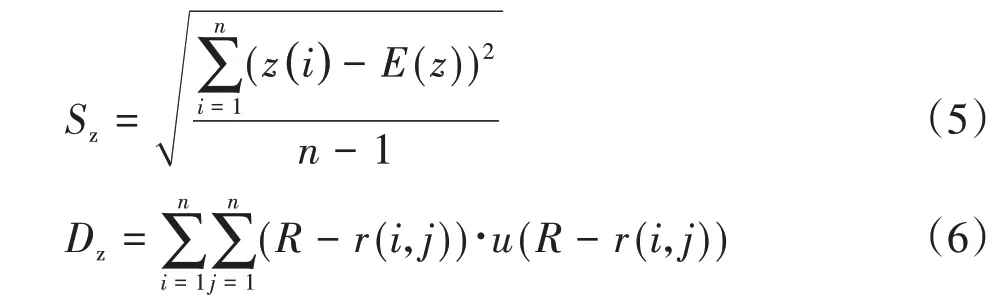
其中，E（z）为序列｛z（i）|i=1，2，…，n｝的评价值；R为局部密度的窗口半径，其选取既要使包含在窗口内部的投影点的平均个数不太少，避免滑动平均偏差太大，又不能使其随着n的增大而增大太多，可根据实验来确定；r(i，j)表示样本之间的距离，r(i，j)=|z(i)-z(j)|；u（t）为一单位阶跃函数，当t≥0时，其函数值为1，当t＜0时，其函数值为0。

（3）优化投影指标函数。当各指标值的样本集给定时，投影指标函数Q（a）只是随着投影方向a的变化而变化。不同的投影方向反映不同的数据结构特征，最佳投影方向就是最大可能暴露高维数据某类特征结构的投影方向，因此可以通过求解投影指标函数最大化问题来估计最佳的投影方向，即：

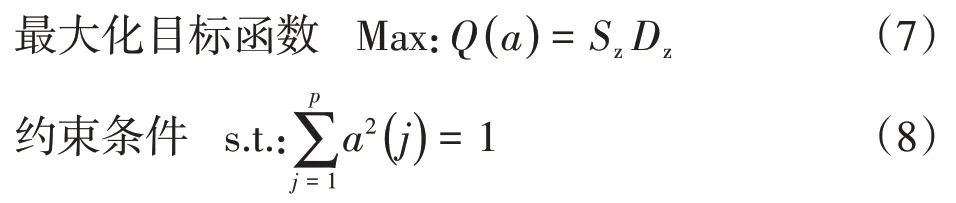
这是一个以｛a（j）|j=1，2，…，p｝为优化变量的复杂非线性优化问题，采用传统的优化方法较难处理。因此，本研究采用模拟生物优胜劣汰与群体内部染色体信息交换机制的基于实数编码的RAGA来解决高维全局寻优问题。

1.2 基于实数编码的RAGA

RAGA［14］是一种改进的基于实数编码的加速遗传算法，克服了二进制编码的缺点，使得个体的编码长度等于其决策变量数，由此也使得算法的寻优能力大幅增强。

RAGA模型的建模过程包括以下8个步骤。设求解最优化问题：

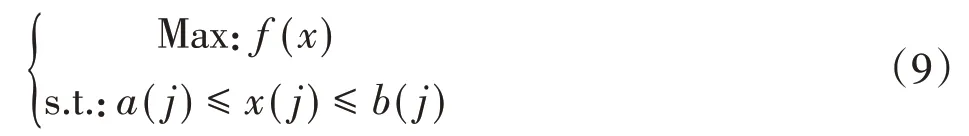
（1）优化变量的实数编码，在所有优化变量的取值区间内产生均匀分布的随机变量。

（2）将父代种群初始化，即将产生的均匀随机数优化后，计算得到目标函数值，并进行从大到小的排序。

（3）计算父代种群的适应度评价，即计算基于序的评价函数（用eval（v）表示）。

（4）进行选择操作，产生新的种群。

（5）对步骤（4）中产生的新种群进行交叉操作。

（6）对步骤（5）中产生的新种群进行变异操作。

（7）计算经遗传进化得到新个体的适应度函数并排序，确定优秀个体。

（8）遗传算法加速。

上述前7个步骤构成标准遗传算法（Standard Genetic Algorithm，SGA）。由于SGA寻优效率的有效性较差，不能保证全局的收敛性。因此，将SGA进化所产生的优秀个体变化区间作为下次迭代时优化变量的新变化空间后，算法转入步骤（1），开始下一代的SGA进化迭代计算。

在步骤（8）中，优秀个体的变化区间逐渐缩小，与最优点的距离将越来越近，算法因此加速运行，直到最优个体的目标函数值小于某一设定值或算法运行达到预定的加速次数时，算法结束。以上8个步骤构成了基于实数编码的RAGA。

1.3 分类及综合评价分析

建立PPC模型时，将最大化的投影指标函数Q（a）作为目标函数，并将各个指标的投影方向a（j）作为优化变量，运用RAGA算法求出最佳投影方向a'，再用a'计算各样本的投影值z（i）。然后根据各样本的投影值对其进行分类，同时通过最佳投影方向的值来对分类结果的合理性进行综合分析。

2 应用实例与结果分析

2.1 应用实例

我国造纸工业所用植物纤维原料种类繁多，大致可分为木材纤维原料、非木材纤维原料和半木材纤维原料三大类。水分、灰分、1%NaOH抽出物、聚戊糖、木质素和纤维素作为植物纤维原料中不可或缺的物质，对植物的生长发育起着重要的作用，同时对造纸工艺过程的制定和工艺参数的调整有直接影响［18-19］。本研究选用文献［18］中木材纤维原料（包括针叶木纤维原料和阔叶木纤维原料）和非木材纤维原料（禾本科纤维原料）的数据，建立用于常见造纸纤维原料分类的RAGA-PPC模型并进行综合评价，选定水分C1、灰分C2、1%NaOH抽出物C3、聚戊糖C4、木质素C5、纤维素C6 6个主要指标作为评价因素，具体数据如表1所示。

2.2 PPC模型的建立

对表1中的15种造纸纤维原料通过投影寻踪算法建立综合分类评价的PPC模型。在实施RAGA的过程中，选取父代的种群规模为n=380，交叉概率pc=0.80，变异概率pm=0.80，选取了20个优秀的个体，加速次数为6次，加速循环280次。经计算得到最大的目标函数值为0.4461，最佳投影方向为a'=（0.0390，0.2500，0.5137，0.8203，0，0.0198），将a'和表1中各样本指标值代入式（3）后可得到15种造纸纤维原料的综合评价投影值z（i）=（0.2103，0.1531，0.2104 ，0.2558，0.2103，0.2103，0.2104，1.0308，0.7646，1.1396，0.9796，0.9280，1.2770，1.3854，1.3825）。

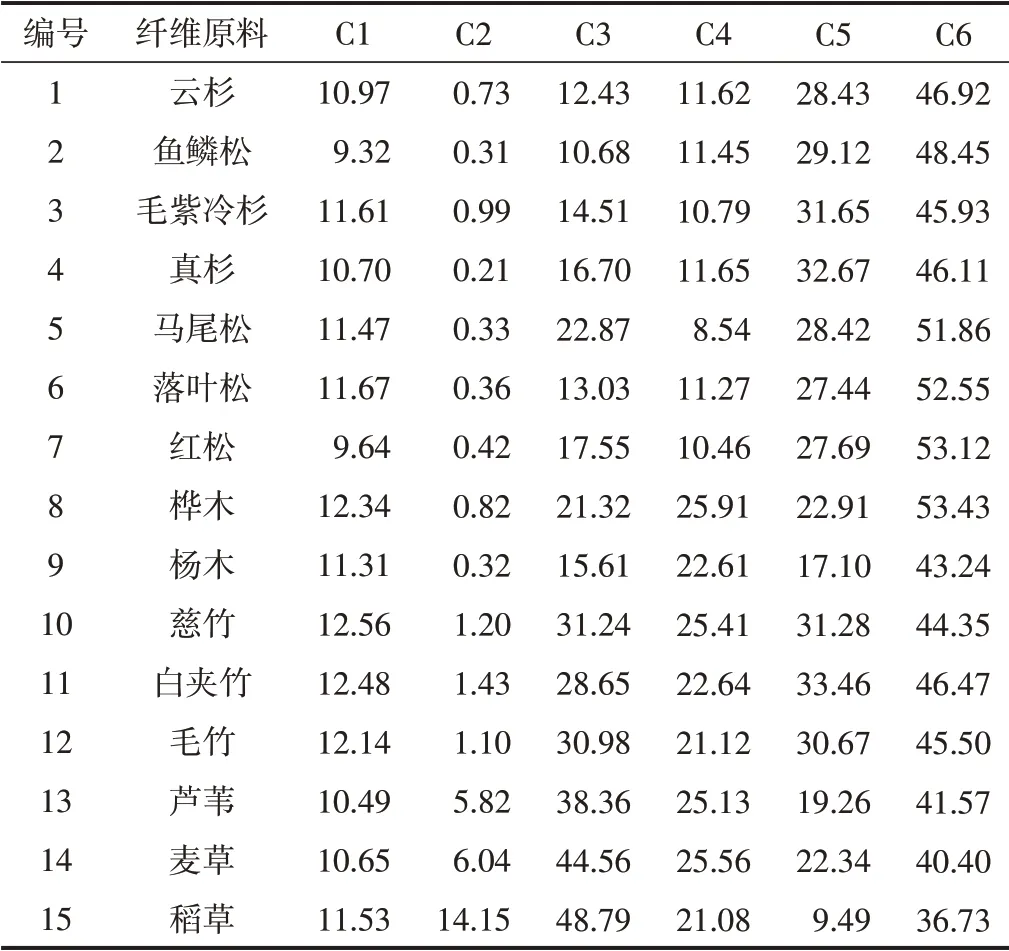
表1 我国造纸纤维原料及其主要化学成分 %

为了对15种造纸纤维原料进行正确的分类，将投影值z（i）从大到小进行排序，并结合样本序号作散点图（如图1所示），利用这组散点数据则可建立相应的PPC评价模型。

2.3 RAGA-PPC模型建立与结果分析

利用RAGA-PPC模型，得到各种造纸纤维原料的投影值，将投影值和样本序号建立关系，得到如下模型y*(i)：

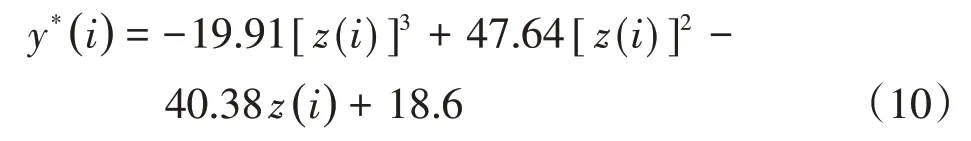
该模型拟合曲线（见图1）的复相关系数达0.9243。利用模型y*(i)计算15个造纸纤维原料序号对应的值，预测结果列于表2的第3列，实际序号与计算值的平均绝对误差为0.9808，平均相对误差为14.40%，说明在遗传算法下建立的RAGA-PPC模型拟合精度较高。对照表1和图1也可以看出，同一类别造纸纤维原料的投影值相差小，且散点分布位置相距较近而呈聚集状态。其中，1#云杉、2#鱼鳞松、3#毛紫冷杉、4#真杉、5#马尾松、6#落叶松和7#红松的投影值比较相近，散点分布在图1的左上方，它们同属于针叶材。草类则位于右下方。10#慈竹、11#白夹竹和12#毛竹的投影值很接近，同属于竹类，并与8#桦木和9#杨木的投影值也很接近，散点聚集于图1中间，但两者与针叶材和草类区分明显。

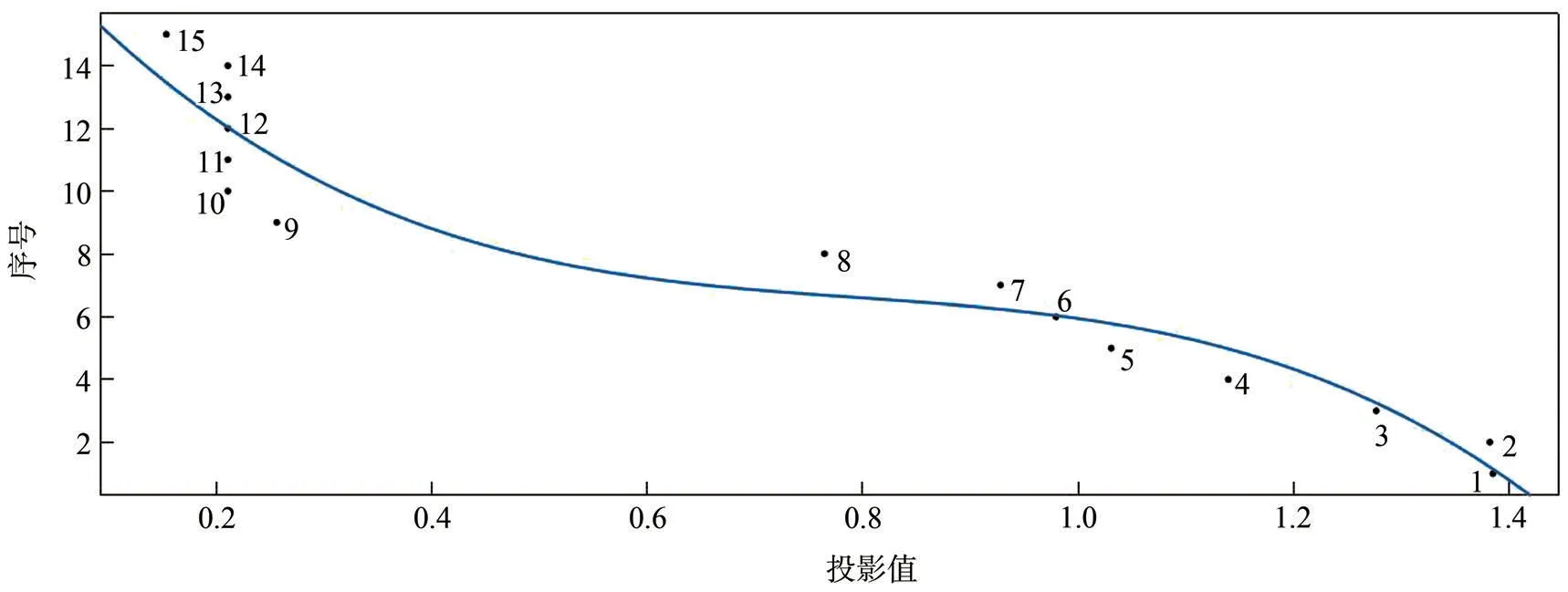
图1 15种造纸纤维原料投影值与样本序号散点图

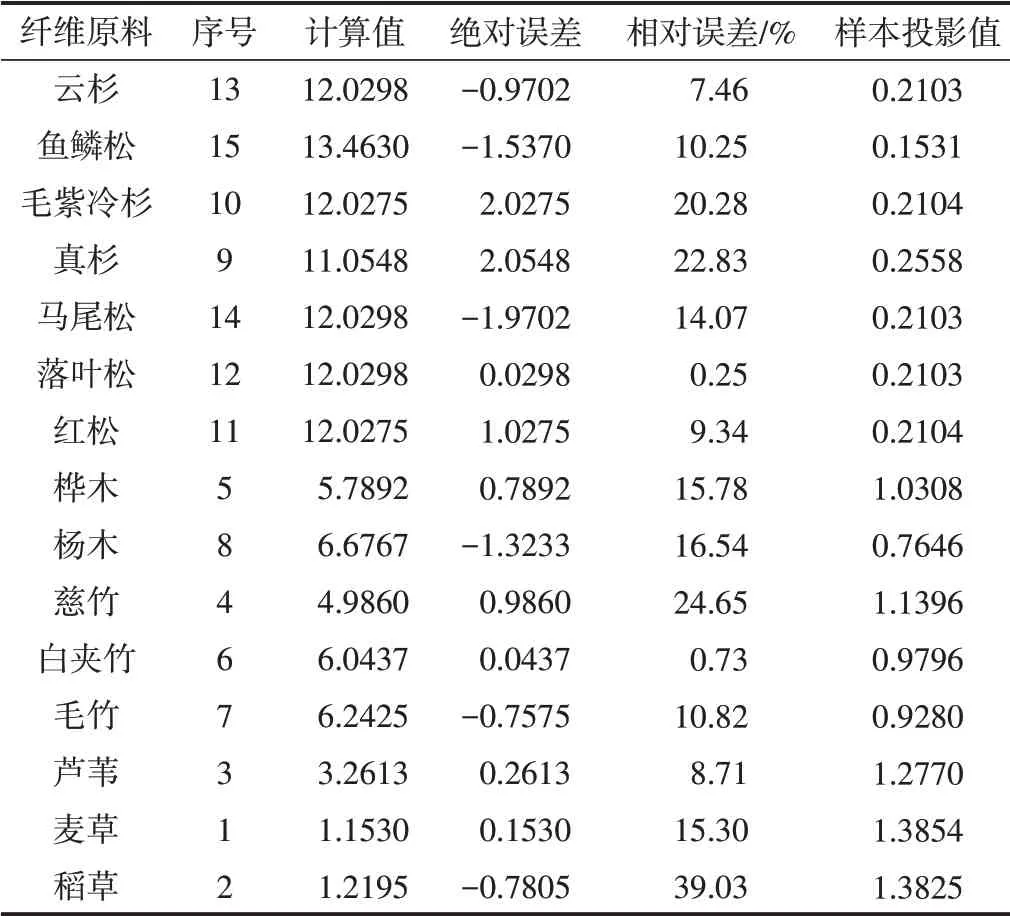
表2 我国造纸原材料划分RAGA-PPC模型计算结果

因此，利用RAGA-PPC模型可较好地表达针叶材、阔叶材、竹类和草类这4类造纸纤维原料的主要类别特性，预测结果具有较好的精度和可解释性。为验证模型的有效性，选取文献［18］中的另4组数据并代入RAGA-PPC模型预测类别，结果如表3所示。步骤如下：先利用前面通过优化计算得到的最佳投影方向a'=（0.0390，0.2500，0.5137，0.8203，0，0.0198）计算4组样本数据的投影值，再将投影值代入模型y*(i)（见式（10））中，根据计算值在图1中所处的编号区间确定4组样本的类别归属，结果如表4所示。从表4可以看出，RAGA-PPC模型能够有效地区分各类不同的造纸纤维原料。尽管蔗渣在生物学上属于草类，但由于其灰分比草类低（通常为稻草的1/5，麦草的1/3～1/2），验算结果表明其化学组成分类特性更接近于竹类。

利用RAGA-PPC模型不仅能很好地对各类造纸纤维原料进行分类识别，而且还能根据最佳投影方向的大小，分析出各评价指标对造纸原材料分类评价的影响大小，并解释其中存在的差异性。图2为各评价指标及其最佳投影方向a'直方图。由图2可以看出，戊聚糖、灰分和1%NaOH抽出物是影响造纸纤维原料分类的重要因素。戊聚糖含量可近似地反映原料中半纤维素的含量。在各种造纸纤维原料中，针叶材的戊聚糖含量最少，而阔叶材中的戊聚糖含量与竹类、草类的戊聚糖含量相近。从图1可以明显看出，由于戊聚糖含量的差异，针叶材分布的位置与阔叶材相距较远，阔叶材分布的位置与竹类、草类相距较近。对于针叶材和阔叶材来说，燃烧后产生的灰分较少，较难蒸煮，而草类产生的灰分较多，较易蒸煮；而竹类的灰分介于草类和木材类之间，蒸煮难度也介于两者之间。由图1可以看出，竹类的散点分布位置介于草类和阔叶材之间，与实际情况相符。木材中的1%NaOH抽出物主要分为萜类化合物、脂肪族化合物和芳香族化合物。萜类化合物主要存在于针叶材的抽提物中，脂肪族化合物多存在于竹类和草类的抽提物中，针叶材和阔叶材中都含有芳香族化合物。因此，造纸纤维原料抽出物中的化学成分差异性也是导致分类结果不同的重要因素。

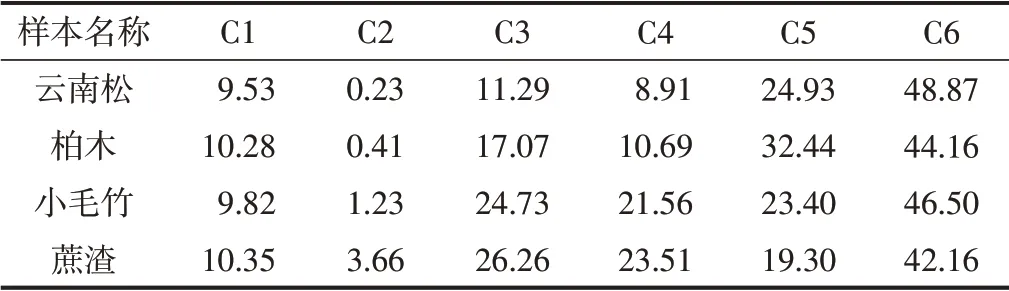
表3 选取进行模型验证的我国造纸纤维原料及其主要化学成分 %

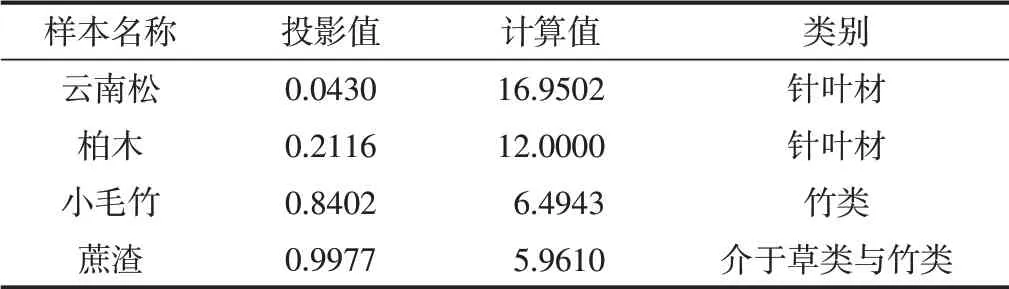
表4 模型验证计算结果及分类结果

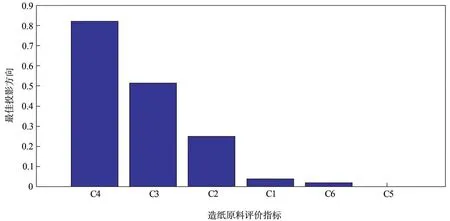
图2 造纸纤维原料评价指标与最佳投影方向直方图

3 结 论

采用基于实数编码的加速遗传算法投影寻踪（RAGA-PPC）模型，将各种造纸纤维原料的多维评价指标综合成一维投影指标，建立了造纸纤维原料的评价模型，并进行了有效分类和综合评价。实例研究结果表明，RAGA-PPC模型能找到各造纸纤维原料评价指标的最佳投影方向，且该方向可较好地反映造纸纤维原料的主要分类特性。RAGA-PPC模型预测计算简单，分类正确，可解释性强，并能直观地看出投影分类后造纸纤维原料的分布情况，为涉及造纸纤维原料多因素、多样本的分类和综合评价提供了新途径。