基于主元分析方法的化工过程故障诊断与识别
2020-10-27刘丽云牛鲁娜栗月姣胡海军
刘丽云 国 蓉 牛鲁娜 栗月姣 胡海军
(1.西安工业大学光电工程学院;2.中国石化青岛安全工程研究院;3.西安交通大学化学工程与技术学院)
石油炼化等化工行业是我国国民经济的支柱产业,但每年化工企业大小事故频发,引发的火灾、 爆炸及泄漏等事故造成社会经济损失严重,甚至会危及人员健康安全[1],如2018年3月12日,江西九江某石化企业未及时发现柴油加氢装置原料缓冲罐的泵出口单向阀失效引发爆炸着火事故,造成2人死亡、1人轻伤。 为了减少事故的发生,需要对化工设备进行在线、离线监控,当监控量偏离设定范围时及时预警,从而使企业能及时调整设备工况或停机,保证设备安全。 企业通常选择动态监测生产过程的方法, 如监测孔法、挂片法、电阻探针法及电化学法等[2]。 但是,国内企业由于技术条件和经济条件限制,很难建立集成化、 网络化且较全面的故障诊断与识别系统,对于故障发生的诊断与识别能力不足,化工过程故障的诊断与识别问题仍亟待解决。
通常,企业会积累多年的设备运行过程历史数据,而这些数据往往用于对某些影响化工设备过程发展的单一因素分析,或者用于建立少量因子的模型[3],企业希望通过这些方法结合过程机理,从而尽可能及时地排除故障。 但现代化设备变得日益复杂化和大型化,伴随的过程故障发生的随机性更大、种类更多,产生的海量数据信息更加复杂多样,合理有效地利用历史数据进行化工过程故障诊断与识别得到了更多的关注。
随着大数据技术的发展,各个行业开始通过研究积累的海量数据, 发现数据内部隐含的信息,探索数据内部之间的关系,判断事物发展走势并预测过程发展趋势,从而做出更为客观可靠的决策推动事物发展[4]。 大数据技术在医疗、交通、 人才培养及电力等众多领域已经有所应用,如刘广涛发现大数据应用于智慧交通可以解决城市拥堵问题[5];梁丽业和何业辉将大数据应用于医院病例整理,优化了整理过程,减少了人力消耗与出错[6];王伟发现将大数据应用于电网建设可以有效支撑智能电网运行[7]。 大数据技术相比于传统技术具有很多优越性,如分析内容的范围更广泛全面,分析内容的时间跨度更长,具有一定的预测性质,因此可以将它应用于化工过程故障的诊断与识别,通过化工过程数据的内部信息,客观准确地判断故障的发生,为企业预防故障发生提供依据。
常用的基于数据驱动的故障分析方法[8]包括主 成 分 分 析 (Principal Component Analysis,PCA)、偏最小二乘法(Partial Least Squares,PLS)、独立成分分析 (Indenpent Component Analysis,ICA) 及Fisher 判 别 分 析 (Fisher Discriminant Analysis,FDA)等。Hu Z K等提出了递推PCA的故障诊断与隔离方法,能够有效解决实际铅、锌冶炼的5种过程故障误报警与隔离问题[9];Yu J提出了一种基于局部Fisher判别分析的多种故障模式监测方法, 对3种不同测试情形下的故障误诊断率分别为0.0%、9.8%和2.0%[10];Dong J等提出了一种基于全PLS模型的自适应故障监测方法,对田纳西-伊斯曼(Tennessee-Eastman,TE)过程某一质量故障的两个监测统计量的误报警率为0.6%和0.9%[11]。上述基于数据统计的方法都能够针对不同化工过程故障进行不同程度的诊断与识别,但是仍然存在针对因素单一、诊断故障种类偏少及数据“维度灾难”[12]限制等问题。
笔者提出一种基于主元分析的化工过程故障诊断与识别方法,通过对正常工况数据进行统计量计算,确定正常工况数据的阈值;然后计算故障工况数据的统计量,超过阈值的均为故障数据。 同时,通过计算变量的贡献率识别出引起故障的主控变量,当出现故障时,调整该变量数值,可以及时改善运行工况。 将该方法运用于化工行业标准的TE过程数据,希望为行业的过程故障诊断与识别提供依据与借鉴。
1 故障诊断与识别方法
如图1所示,故障诊断与识别过程包括:数据预处理; 计算正常工况数据的统计量T2与SPE阈值[13],统计故障工况数据的统计量值大于阈值的数量,并计算对应的故障发现率(Fault Discovery Rate,FDR)[14], 利用FDR评价PCA方法的故障诊断能力;计算数据集所有变量对故障产生的贡献率,贡献率大的变量即为识别出的引起故障的主控变量。
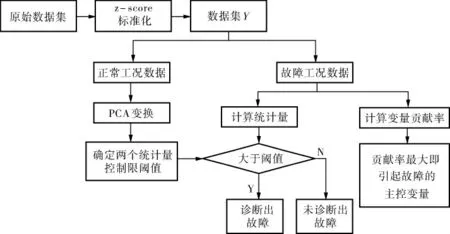
图1 故障诊断与识别流程
1.1 数据预处理
在使用PCA方法进行降维时, 需要将数据标准化为均值为0、 方差为1的标准正态分布数据集,利用零均值(z-score)标准化[15]可以实现,其数学表达为:

其中,Y表示数据集,μ表示Y的均值,σ表示Y的标准方差,X表示预处理后数据集。
1.2 故障诊断与识别
PCA可以将高维过程数据投影到正交的低维子空间,并保留主要过程信息。 几何上,把样本构成的坐标系通过某种线性组合旋转到新的坐标空间, 新的坐标轴代表了具有最大方差的方向。对经过预处理的数据集X(n×m)通过协方差分解确定主元空间,其协方差矩阵S的计算式为:
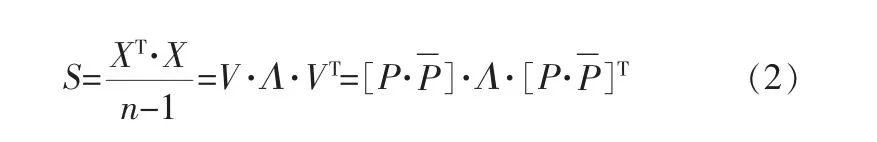
其中,Λ是协方差矩阵S的特征值矩阵, 其对角线上的元素满足λ1≥λ2≥…≥λm;V是协方差矩阵S的特征矩阵;P(m×A)是包含V的前A列的主元信息矩阵;是特征矩阵V余下的m-A列,包含非主元信息。 分解X得到主元子空间矩阵Q(n×A)和残差子空间矩阵E:
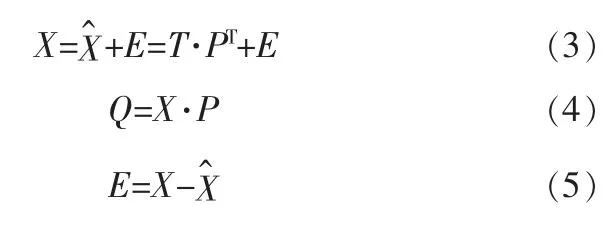

每个变量对SPE和T2的值有贡献率, 检测到故障后, 贡献率值Cont越大的变量被认为是越可能造成故障的变量。 统计量SPE和T2的变量贡献率定义如下:
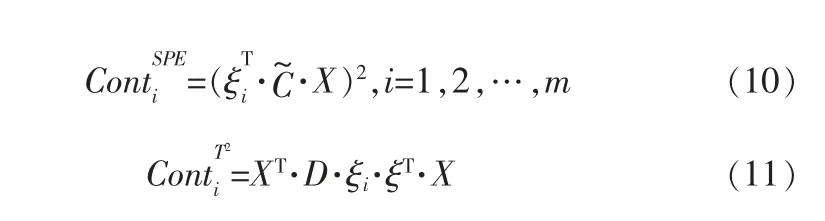
其中,ξi为单位矩阵I的第i列,=I-P·PT,D=PTΛ-1P。
1.2.2 故障诊断与识别结果评价
在机器学习领域,为了保证提出的最优模型的故障诊断效果可靠,将故障发现率作为评价指标,其含义是错误拒绝(拒绝真的(原)假设)的个数占所有被拒绝的原假设个数的比例的期望值[17]。 在故障诊断时,其数学表达式为:

其中,FDR值的范围是[0,1],其值越接近于1,表明诊断效果越好;TN表示被正确分类的故障数据;FN表示被错误分类的故障数据。
每个量的混淆矩阵见表1,针对二分类,建立的分类模型最终需判断当前样本是正或负 (即Positive与Negative),True表示分类正确,False表示分类错误。
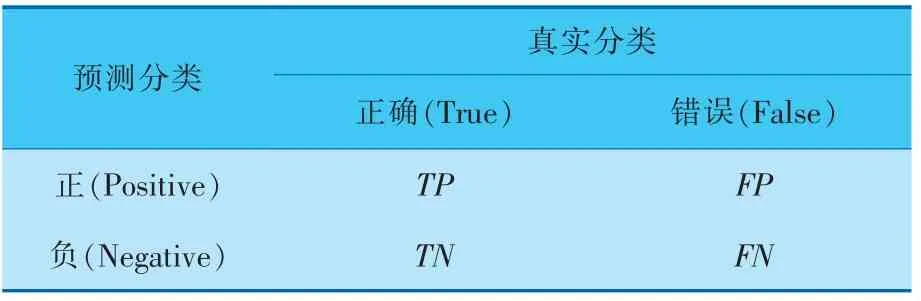
表1 混淆矩阵
2 TE过程故障
TE过程由伊斯曼化学公司创建,是为了给评价过程控制和监控方法提供的一个现实的工业过程,具有一定的代表性。 利用在TE过程仿真中采集的数据来比较各种故障检测和诊断方法的有效性,已在过程监控领域得到了广泛的应用[18]。 TE过程主要由反应器、冷凝器、汽提塔、气液分离塔及压缩机等多个操作单元构成,TE过程流程如图2所示。
TE过程共有4种气体反应物, 分别为A、D、E和C,这4种反应物中分别都含有少量的惰性气体B。 在催化剂的作用下,反应器中主要有4个同时进行的化学反应,其中的两个主化学反应生成的液态产物分别为产物G和产物H,同时会生成副产物F,化学反应方程式如下:
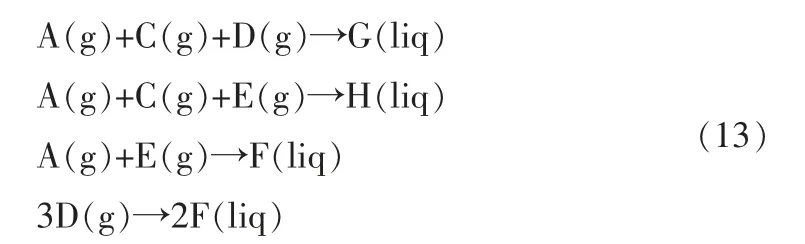
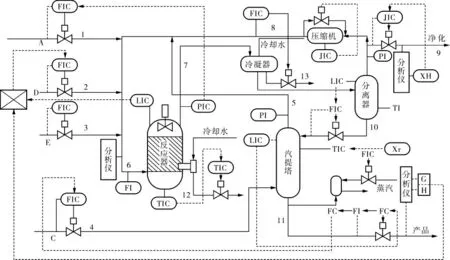
图2 TE过程流程
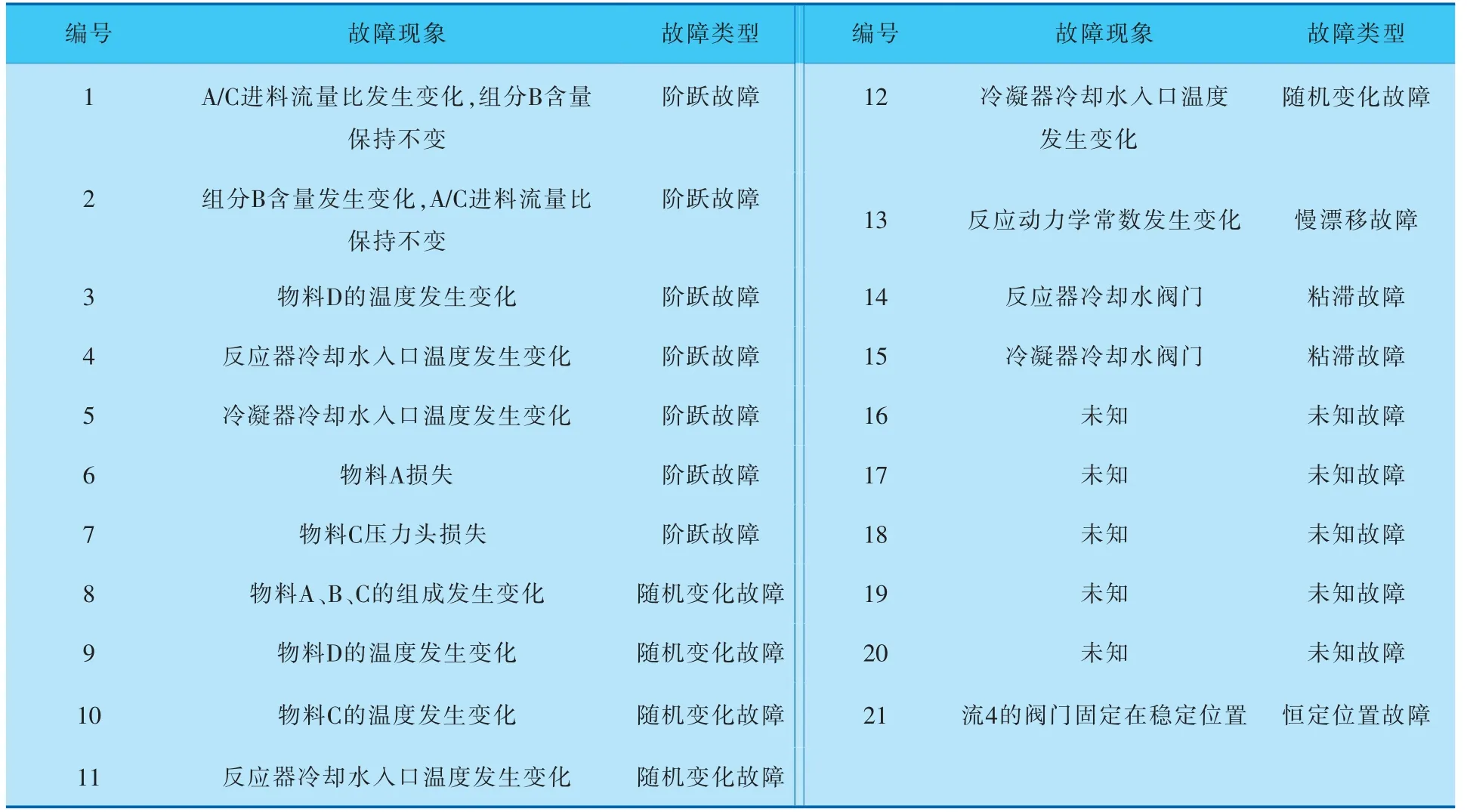
表2 TE过程故障
TE过程设定的故障见表2, 包括21种可操作的故障工况。 21种工况下的采样时间间隔为3min。 在正常工况下,过程运行48h产生的960个数据被采集作为正常数据样本。 21种故障工况在过程稳定运行8h后引入, 故采集的960个数据中前160个数据不含故障, 后800个数据含有故障。将正常工况下的960个数据作为训练样本, 故障工况下的800个数据作为测试样本。 故障模式1~7是关于过程变量的阶跃故障,故障模式8~12是随机变化故障,故障模式13是反应动力学的慢漂移故障,故障模式14~15是相应的粘滞故障,故障模式16~20是未知故障, 故障模式21为恒定位置故障。
TE过程数据的正常状态与21种故障都有52个变量,其中包括41个过程变量(22个测量变量和19个成分变量)和11个操作变量,具体信息见表3。

表3 TE过程的变量
3 故障诊断与识别结果
TE过程包含的故障有六大类,笔者选择阶跃故障1、随机变化故障12、慢漂移故障13、粘滞故障14、未知故障18和恒定位置故障21展示诊断与识别过程, 并以故障1为例具体说明诊断与识别过程。
阶跃故障1:A/C进料流量比发生变化,组分B含量保持不变。
首先, 选择TE过程正常工况的960个数据与故障1工况的480个数据组合,作为预处理数据集进行z-score标准化;然后,将正常集通过PCA确定其统计量的阈值, 对故障集进行故障诊断与识别。 若故障集数据超过阈值,则诊断正确,若没有超过阈值,则诊断错误。
图3为PCA诊断与识别故障类数据的统计量值和贡献率。
根据图3的MATLAB仿真结果可知:当PCA确定的主元个数为31时,T2的控制限为0.056 9,SPE的控制限为10.061 9。 T2与SPE故障诊断率分别为100%与99.85%,诊断出的主控变量分别为16、7、13与2、16、21。
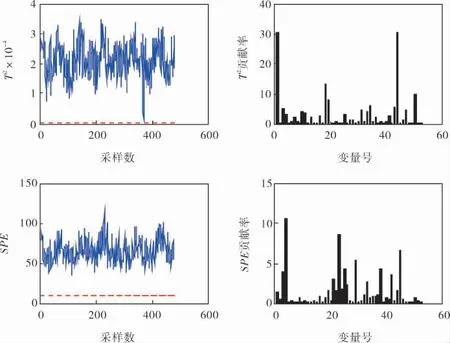
图3 故障1诊断与识别统计量值和变量贡献率
PCA方法对于480个故障数据, 诊断出了478个,具有很高的诊断能力。当TE过程中的A/C进料流量比发生变化,组分B含量保持不变时,反应物的组成成分变化会最先直接影响汽提塔、反应塔相关的变量变化,如变量16(汽提塔压力)、7(反应器压力)及21(反应器冷却水出口温度)等。 同时,为了使反应过程能够改善,就需要对其他反应物和可操作的反应器、汽提塔和分离器进行调节,从而避免更为严重的故障。
对其他5种类型的故障也进行上述诊断与识别过程,当PCA确定的主元个数为31时,T2控制限为0.056 9,SPE的控制限为10.061 9。 图4为5种故障的数据统计量值与变量贡献率。

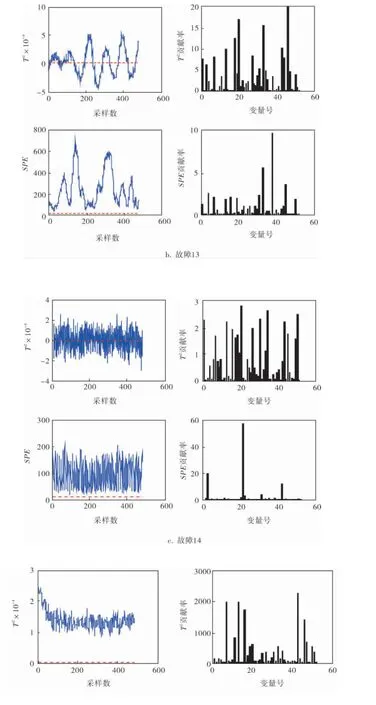
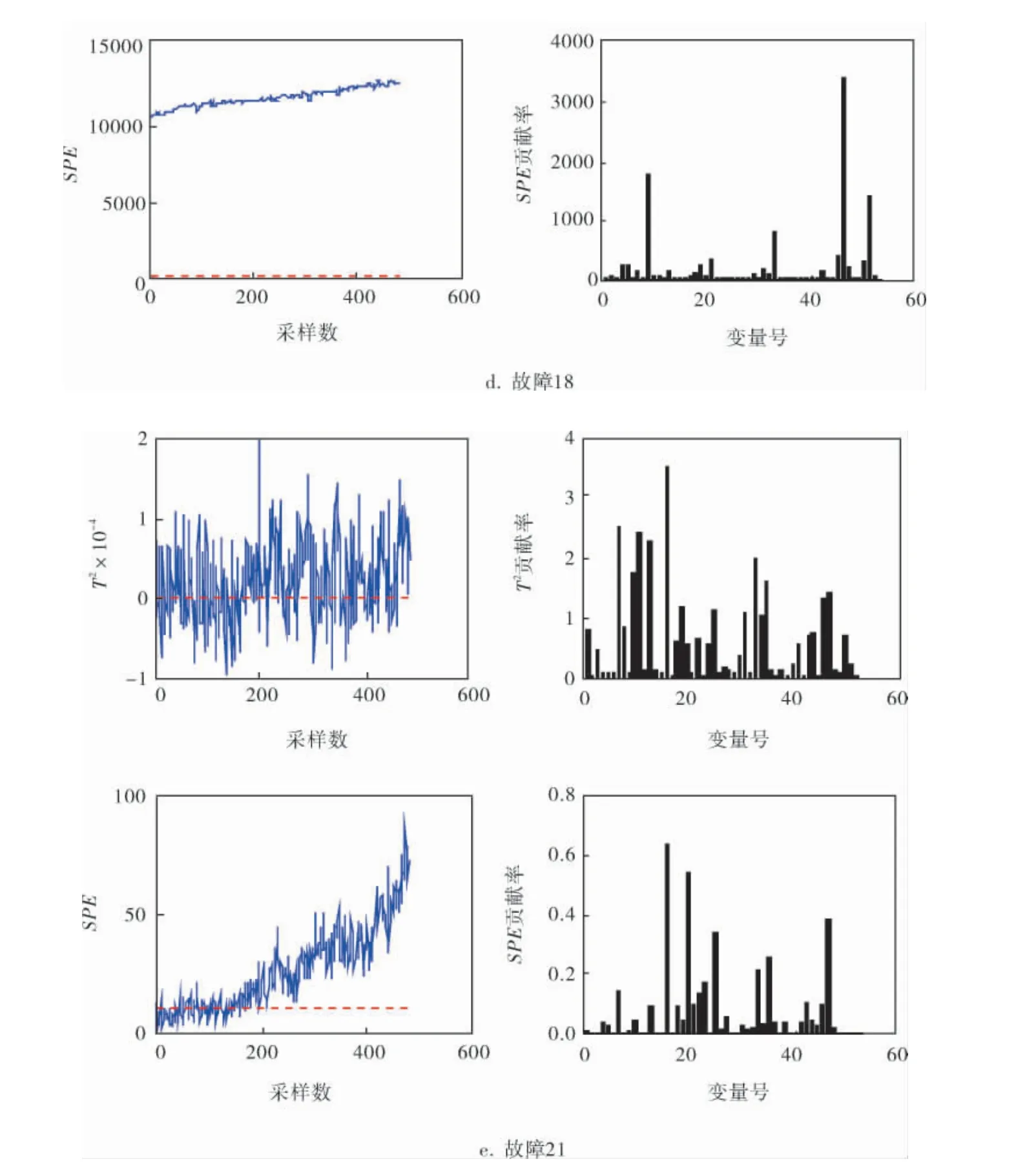
图4 故障12、13、14、18、21诊断与识别统计量值和变量贡献率
由图4可知:
a. 故障12统计量T2与SPE故障诊断率分别为100%与95.62%, 诊断出的主控变量为16、7、13与2、21、16;
b. 故障13统计量T2与SPE故障诊断率分别为100%与98.33%, 对应的主控变量为16、7、13与2、16、21;
c. 故障14统计量T2与SPE故障诊断率分别为100%与99.79%, 对应的主控变量为16、7、13与2、16、21;
d. 故障18统计量T2与SPE故障诊断率分别为100%与82.58%, 对应的主控变量为16、7、13与2、21、16;
e. 故障21统计量T2与SPE故障诊断率分别为100%与20.42%, 对应的主控变量为16、7、13与2、21、16。
统计量T2的结果中,当故障出现时,完全可以诊断出所有故障数据,并且适用于上述5种故障;统计量SPE的结果略微低于T2, 仍然能快速诊断出故障是否出现。 统计量T2主要用于非成分量的变量时,会有很好的表现,而统计量SPE是针对所有类型的变量,由于成分变量的作用,会导致其结果表现较差。
4 结论
4.1 PCA方法通过建立正常工况数据的统计量控制限阈值,能够快速准确地发现过程运行是否发生故障。
4.2 当过程变量仅包含非成分相关的变量时,通过计算统计量T2能够为设备运行提供很好的故障诊断依据;当包含成分变量较多时,可以参考统计量SPE。
