基于小冲杆试验的X80管道钢断裂韧性研究

2020-10-27曹宇光伍志明司伟山李旭阳

中国石油大学学报（自然科学版） 2020年5期

曹宇光, 伍志明, 司伟山, 甄莹, 宋明, 李旭阳, 蒋毅

(1.中国石油大学(华东)储运与建筑工程学院,山东青岛 266580; 2.中国石油西南管道分公司,四川成都 610094)

油气管道的初始缺陷或微裂纹在高压条件下极易发生裂纹扩展,严重影响管道安全运行[1-3],因此对管材性质及断裂韧性进行定量检测十分必要。小冲杆试验技术基于微损试样,不需要对管道进行破坏性取样,有望用于在役管道断裂韧性测试并可最大程度降低对管道的影响。前期利用小冲杆试验获得管材断裂韧性的方法多基于标准试样,并结合二步法[4-5]、等效断裂应变法[6]、应变能密度法[7-9]和反向有限元计算法[10-11]等。标准小冲杆试样不含标准断裂试样类似的裂纹或缺口,难以直接用来确定材料的断裂韧性。Jang等[12]设计了一种带有中心穿透裂纹的小冲杆试样评价材料的断裂韧性,关凯书等[13-19]采用直线缺口及环形缺口的圆形小冲杆试样进行试验和数值模拟,评价了线弹性材料断裂韧性JC。环形预制缺口小冲杆试样已被证明具有一定优势,但缺乏系统的环形预制缺口设计方法,且尚未形成基于该试样获取高韧性管材断裂韧性JC的系统方法。笔者以X80管道钢为研究对象,通过分析试样应力应变状态及损伤断裂设计一种环形缺口小冲杆试样,形成系统的环形缺口小冲杆试样设计方法。基于所设计试样开展小冲杆试验及其数值模拟,采用GTN细观损伤模型[20-22]对试样断裂过程进行模拟并根据单元删除现象判断试样起裂位移。考虑小冲杆试验与标准断裂力学试验在试样、加载方式等方面的不同,建立二者测得的断裂韧性值之间的关联模型,形成一种采用带环形缺口小冲杆试样测试在役管道断裂韧性的方法。

1 标准小冲杆试样试验及数值模拟

1.1 试样制备

小冲杆试验所需试样尺寸极小(试样直径d1为10.0 mm,厚度h在0.300～0.500 mm内)[23-26],使获取在役管材的实际断裂力学性能成为可能。小冲杆试验标准中规定的试样尺寸为:直径d1=10 mm,厚度h=0.5±0.01 mm。按照小冲杆试验标准[27]的要求,以平行于设备表面方向,采用线切割方式从管道上切取直径10.0 mm、厚度0.600 mm的试片,使用砂纸对其进行打磨,去除过热和加工硬化影响区,使试样中不含有任何裂纹和其他宏观缺陷。最终测得3组试样厚度h分别为0.495、0.498、0.499(±0.005) mm。

1.2 试验

如图1所示,小冲杆试验装置冲杆头部为半球形,半径r为1.25 mm,上夹具孔径d2为2.6 mm,下夹具孔径d3为4 mm,上夹具和下夹具倒角半径分别为0.2和0.5 mm。将所加工试样放于下夹具凹槽中,并用上夹具压紧,防止其在试验过程中出现滑动。试验加载时,采用位移控制的方式将冲头对准试样的中心向下施加荷载,加载速率保持在0.2 mm/min,试样变形随着载荷增加不断增大,直至试样破裂,记录整个试验过程试样所受载荷与冲头位移,从而得到载荷位移曲线。

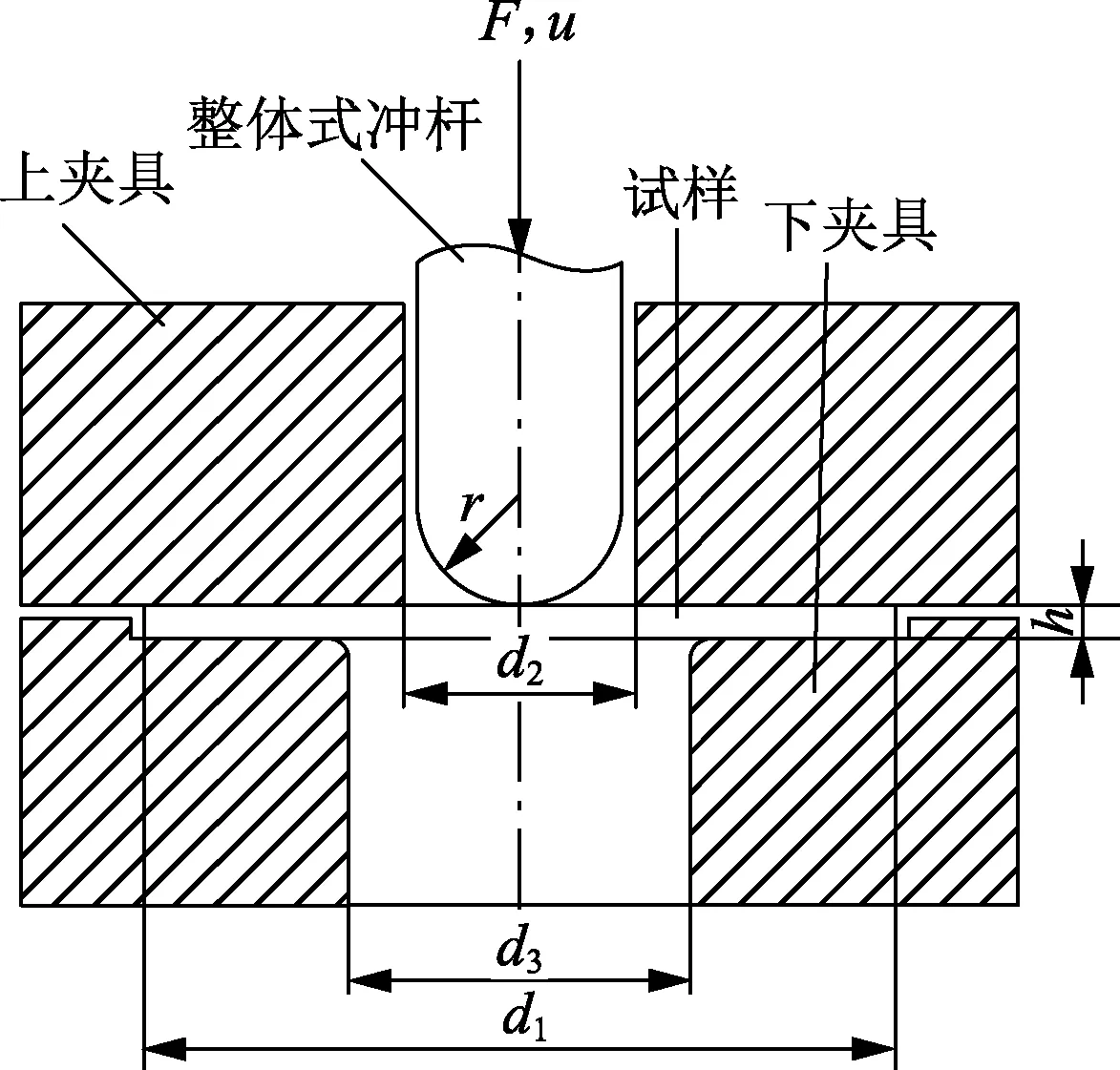
图1 小冲杆试验装置原理图Fig.1 Schematic diagram of small punch test device

1.3 数值模拟

小冲杆试样为圆片式轴对称结构,模型简化为二维轴对称模型。模型尺寸与试验试样一致,试样厚度h为0.5 mm,直径d1取为10 mm,在保证计算精度的基础上,采用四节点缩减积分单元CAX4R对模型进行均匀网格划分;冲头和上下夹具尺寸均与试验装置设为一致,不考虑三者变形,均简化为解析刚体分析。分别对上下夹具施加固定约束,对试样中心边界设置轴对称约束,在试样与冲头夹具之间设置接触。图2为常规小冲杆试验有限元模型示意图。

图2 无缺口小冲杆试验有限元模型Fig.2 Finite element model of small punch test without notch

采用GTN模型模拟小冲杆试验过程中试样的弹塑性变形、损伤与断裂行为。GTN模型是由Gurson提出,后经Tvergaard和Needleman验证和修正的一种表征孔洞演化过程和预测材料的起裂和扩展的细观损伤模型。小冲杆试验有限元模型材料参数的定义分为两部分:一部分是材料弹塑性参数定义;另一部分是材料损伤参数定义。前者以单轴拉伸试验结果为依据,如图3所示;后者结合文献中常用参数并经过大量试算确定,最终确定下的损伤参数模拟结果与试验结果最为接近,如图4所示。

GTN损伤模型屈服函数为

(1)

其中

式中,Req为宏观Mises等效应力;ReL为材料屈服强度;RH为宏观静水应力;q1、q2、q3为材料损伤参数,分别为1.5、1、2.25;f*为孔洞体积分数;fc和fF分别为临界聚合孔洞和断裂孔洞体积分数,分别为0.03和0.15。

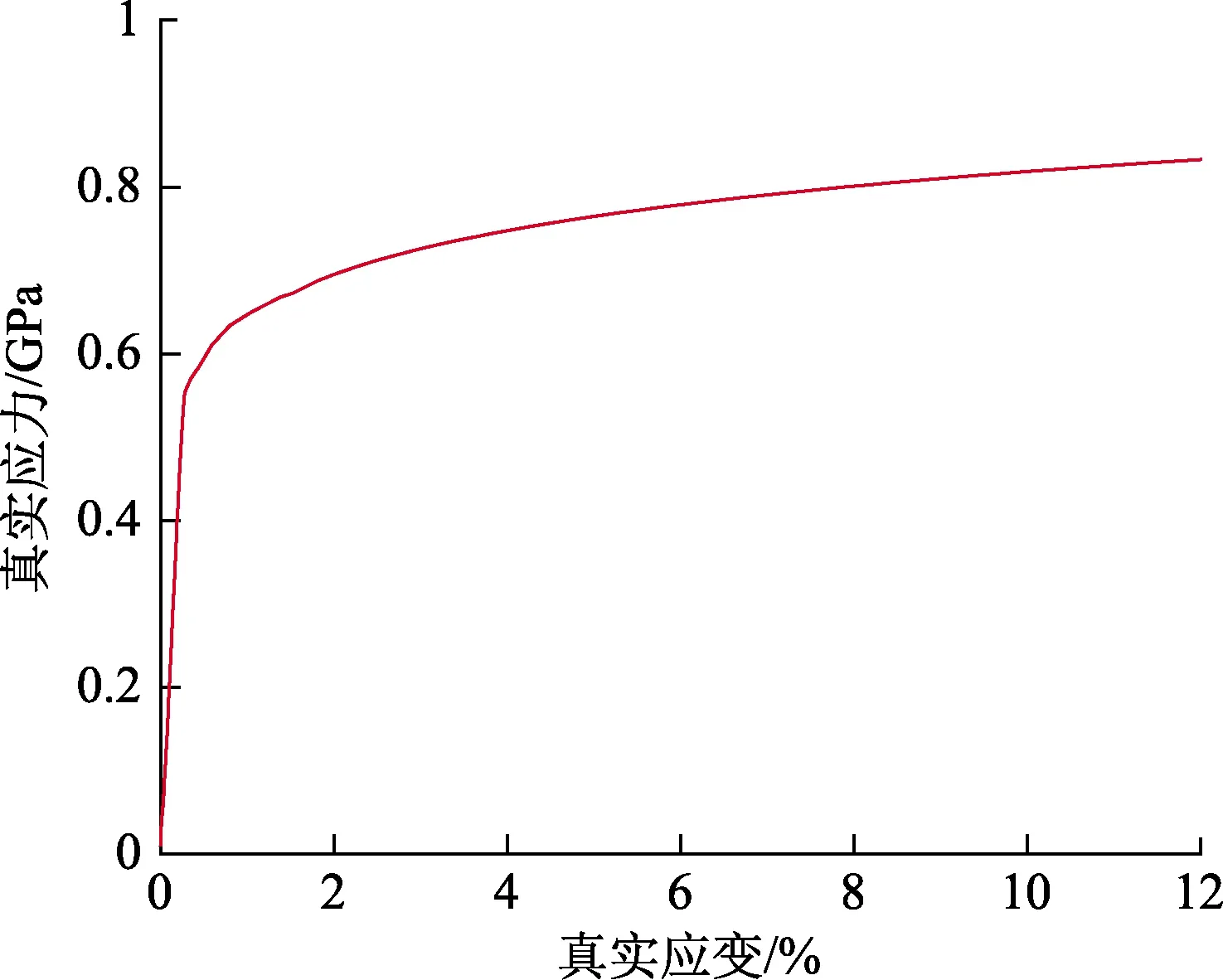
图3 X80管道钢真实应力应变曲线Fig.3 True stress strain curve of X80 pipeline steel

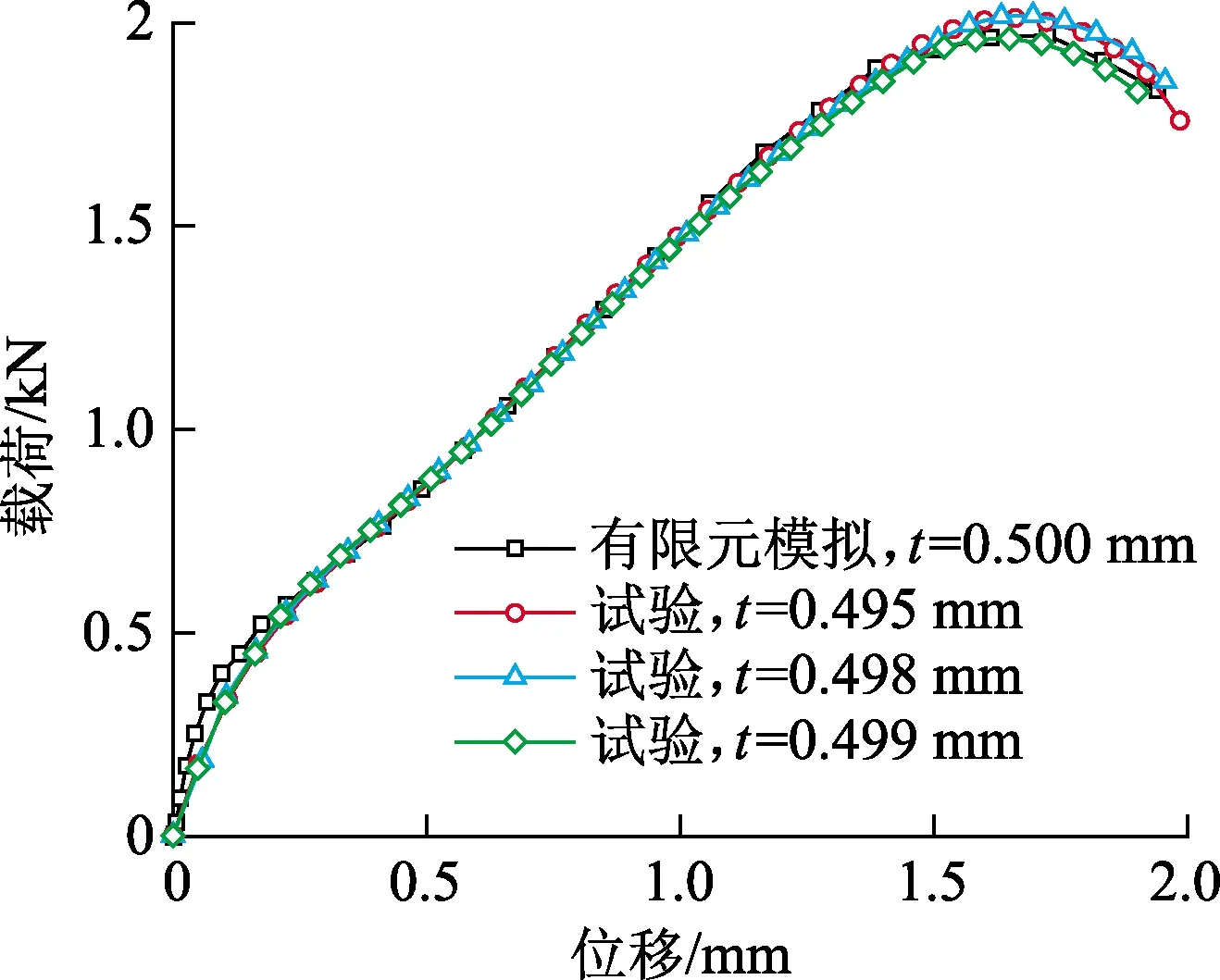
图4 标准小冲杆试验及数值模拟载荷位移曲线Fig.4 Load displacement curves of standard small punch test and numerical simulation

孔洞演化包含孔洞增长和新孔洞形成两部分,孔洞体积分数增长率为

(2)

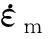
2 环形预制缺口小冲杆试样设计

环形预制缺口小冲杆试样示意如图5所示,其缺口方向符合标准小冲杆试样断裂规律,且试样依然保持轴对称形式,使缺口处于平面应变受力状态,从而具有更好的约束效应,增强了与传统试验断裂韧性的可比性。同时,其轴对称特性能够大大简化有限元模型及受力分析的难度。

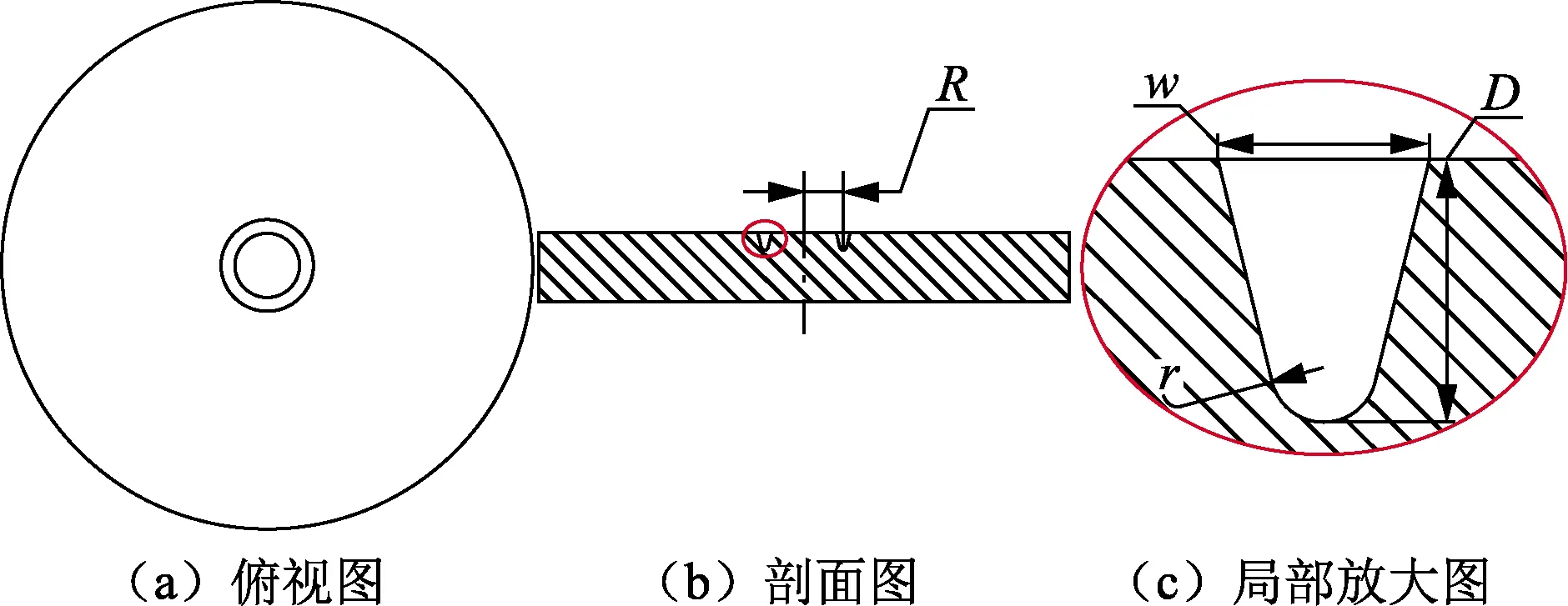
图5 环形预制缺口小冲杆试样示意图Fig.5 Schematic diagram of small punch specimen with circular preformed notch

环形缺口的加工需要确定4个参数,分别为缺口深度D、缺口位置(半径)R、缺口尖端半径r与缺口底部宽度w。为方便环形缺口与标准小冲杆试样(0.5 mm厚)对比及保证两者承载力的一致性,同时考虑小冲杆试验装置的夹持能力,将试样整体厚度h取为0.6 mm,缺口深度D取为0.1 mm。为确定环形缺口位置,对厚度为0.6 mm的完整小冲杆试样断裂过程进行数值模拟,材料参数及模型设置均与标准试验一致,得到试样等效塑性应变云图如图6所示。当位移载荷增加至1.78 mm时,试样在最大等效塑性应变处出现单元消除的现象,通过测量确定此处距试样中心为0.74 mm。因此,可将环形缺口初步定位在以试样中心为圆心半径R(R为0.74 mm)处。为满足J积分计算时的奇异性要求,需要保证缺口尖端半径r足够小,一般不能大于10 μm[17],取为5 μm。缺口底部宽度w若取值太大会影响裂纹尖端应力分布,不利于形成应力集中,而当其取值在小于等于200 μm的范围内变化时对试验影响不大[16],因此取缺口底部宽度w为100 μm。至此,决定环向缺口位置及尺寸的4个参数均已确定。

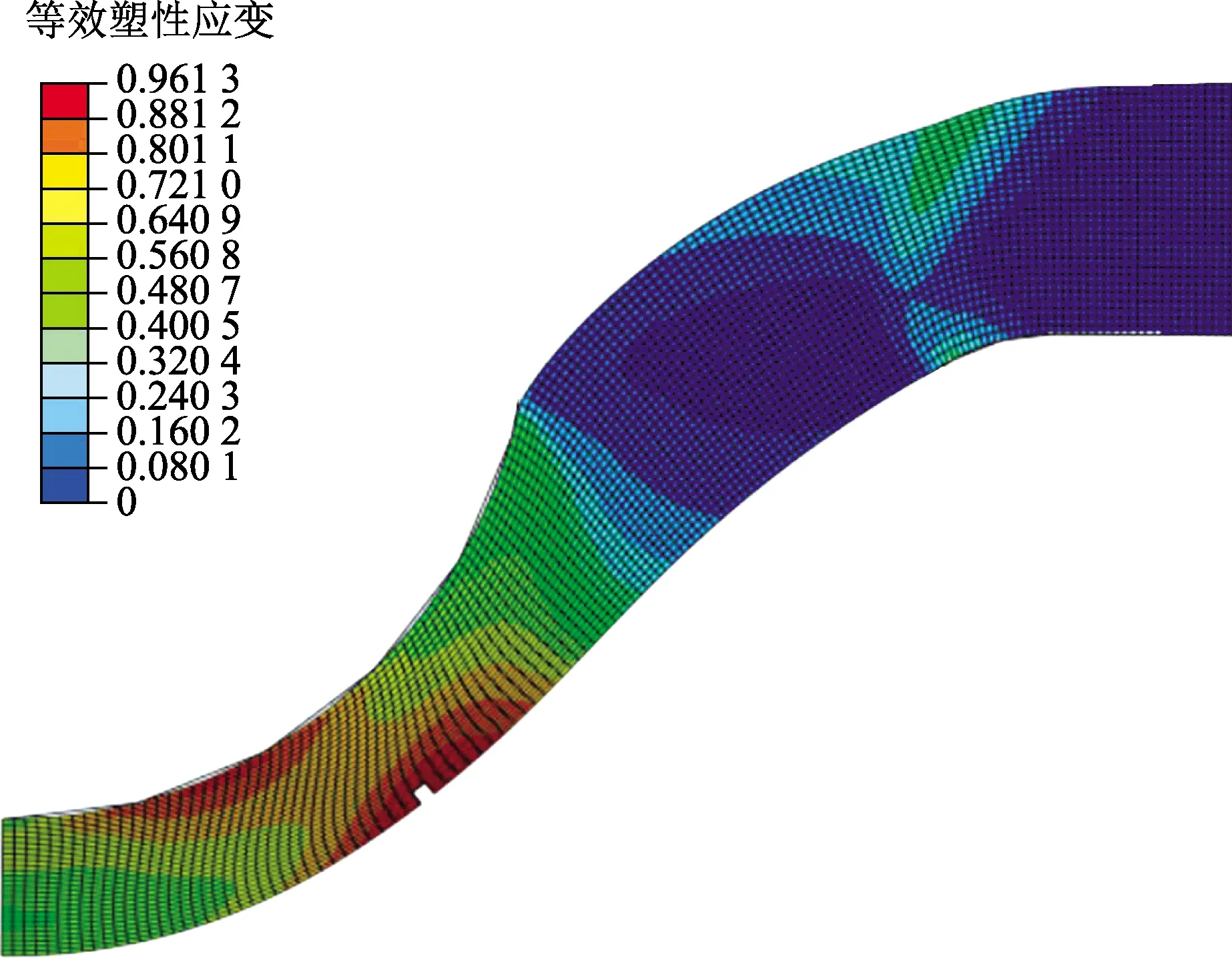
图6 0.6 mm厚未开缺口小冲杆试样等效塑性应变分布Fig.6 Equivalent plastic strain distribution of 0.6 mm thick notched small punch

为进一步验证上述参数尤其是预制缺口位置的有效性,对厚度为0.6 mm不同位置处加工有环形预制缺口的小冲杆试样断裂过程进行模拟。预制缺口尖端半径r与缺口底部宽度w分别取为5和100 μm,环形缺口半径R在0～2 mm内以0.05 mm为间隔取值,模拟结束后分析试样实际断裂位置与预制缺口位置的关系。从模拟结果中可知：当预制缺口半径R取值在0.2～1.3 mm时,试样在预制缺口处发生起裂与裂纹扩展,并发生断裂;当预制缺口半径R小于0.2 mm时,试样在其外侧开裂并断开;当预制缺口半径R大于1.3 mm时,试样在其内侧开裂并断开。图7为4种不同环形预制缺口半径取值对应的试件断裂情况。因此可以认为前文所确定的预制缺口半径为0.74 mm是合理的,试样会在此处发生起裂及裂纹扩展。

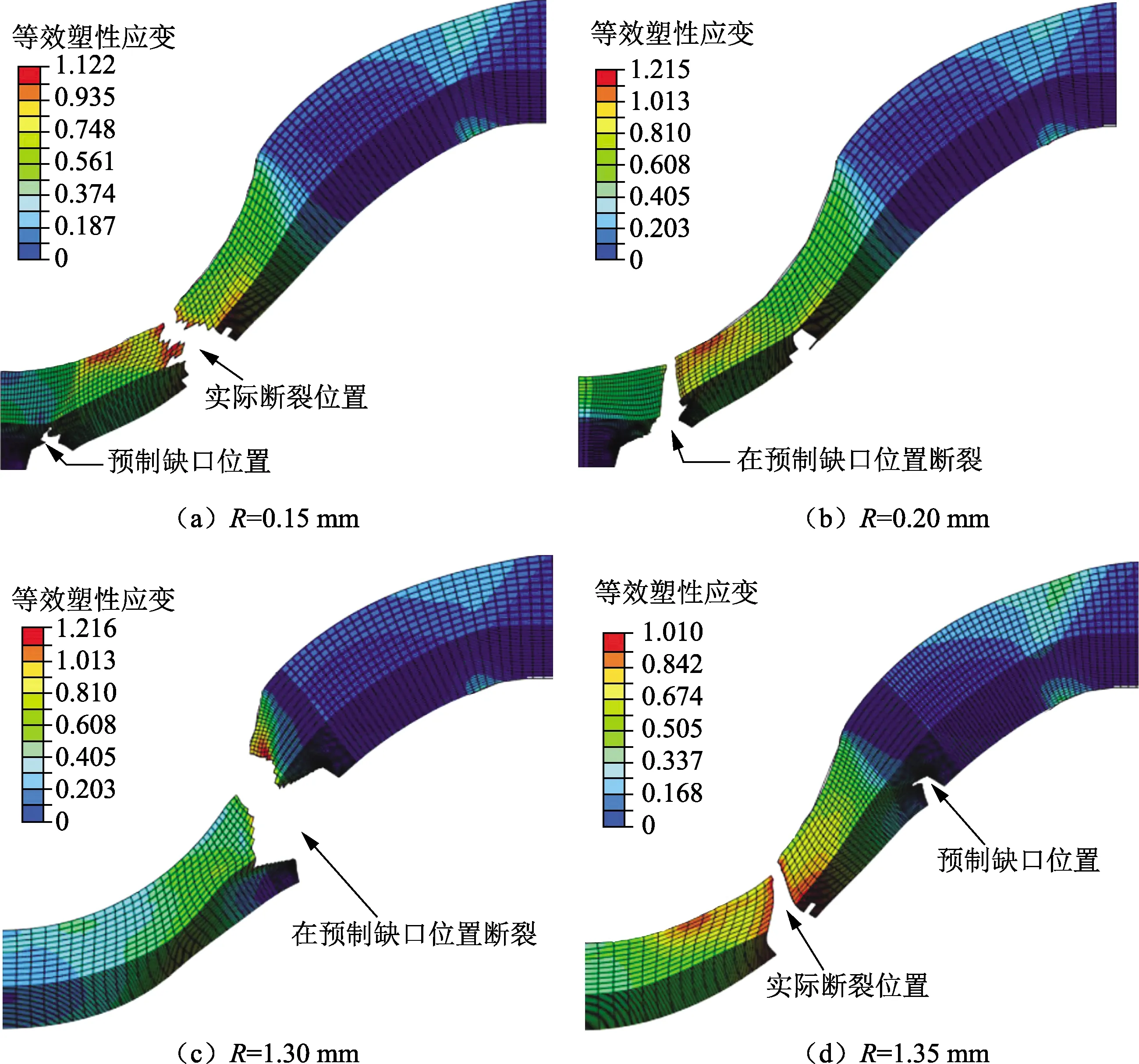
图7 不同缺口半径下小冲杆试样的开裂情况Fig.7 Cracking of small punch specimen with different notch radius

3 环形预制缺口小冲杆试样试验及数值模拟

3.1 试样制备

取样时避开待测材料的腐蚀层,使用线切割的方法以平行于设备表面的方向取下试片,经过初步加工为圆片试样;经过不同粗糙度的砂纸进行打磨,得到圆片试样的尺寸为直径10 mm,厚度(0.6±0.01) mm。最后采用激光切割的方法在圆片试样上加工环形预制缺口,环形预制缺口以圆片中心为圆心,半径R为0.74 mm,缺口深度D为0.1 mm,缺口底部宽度w小于100 μm,缺口尖端半径r小于5 μm。对圆片试样尺寸进行测量,3组试样厚度分别为0.595、0.599和0.600 mm,均符合试验标准。图8为加工后试样及其环形缺口截面形貌。

3.2 试验及数值模拟

利用标准小冲杆试验装置按照标准[27]进行试验,将预制缺口小冲杆试样缺口面朝下对中平稳放置,用夹具将其固定,冲杆以0.2 mm/min速度下压至试样断裂,得到试验载荷位移曲线。利用GTN模型对试验过程进行模拟。将试样的缺口尖端位置简化为半径为5 μm圆弧,由于此处应力应变变化较大且变形严重,为得到准确的有限元分析结果,对其局部网格进行细分,试件网格划分情况如图9所示,其他设置与标准小冲杆试验数值模拟一致。

将环形缺口小冲杆试验与数值模拟所得载荷位移曲线进行对比(图10)。从图10中可以看出,曲线整体吻合度较好,证明了数值模拟的可靠性,但在位移施加初期,两者曲线存在一定差别。这是由于试样加工存在误差,无法保证激光加工缺口的深度与有限元模型完全一致,所以导致曲线无法完全重合。

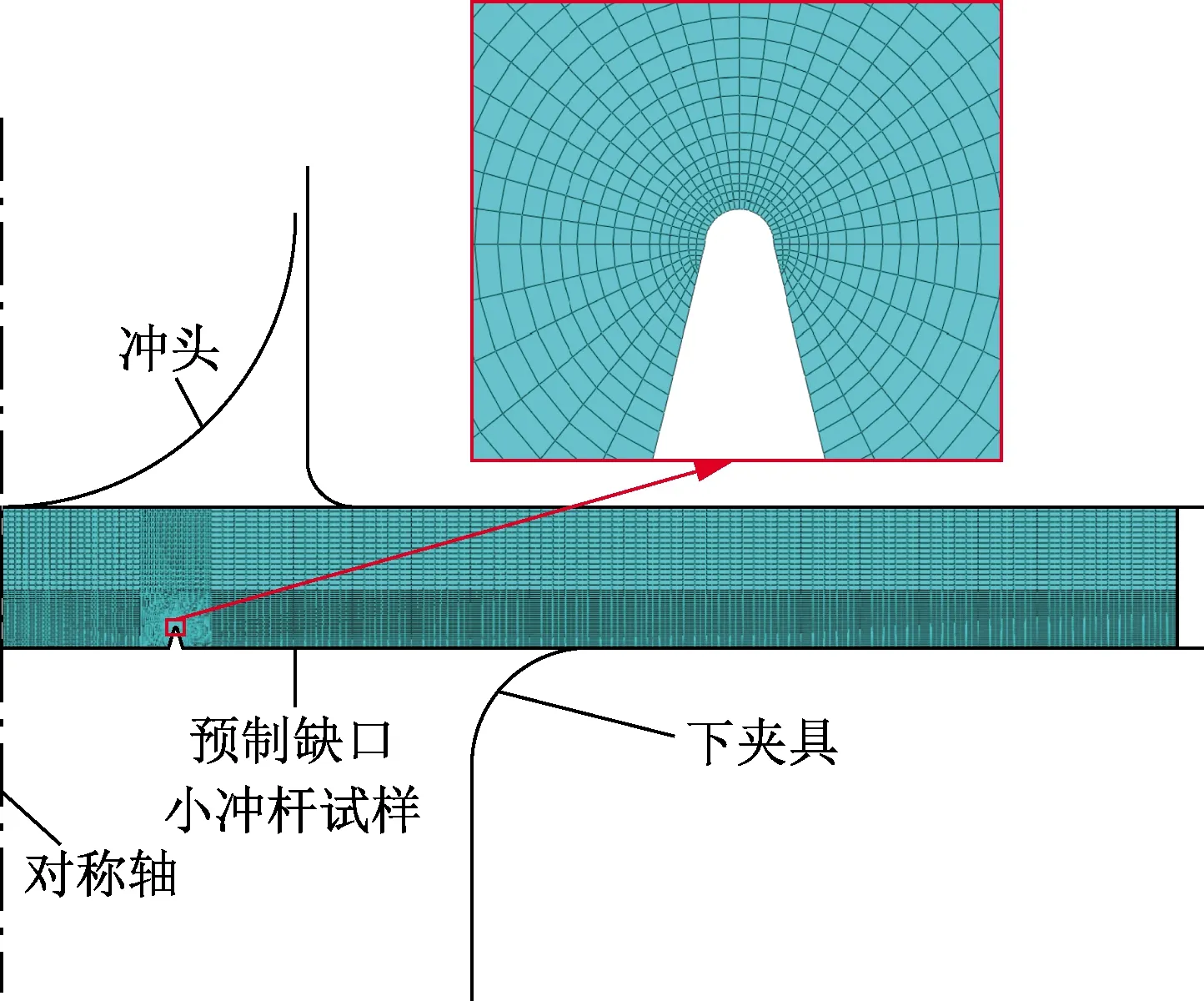
图9 环形缺口小冲杆试样有限元模型网格划分Fig.9 Mesh generation of finite element model of small punch bar with circular notch

图10 试验与数值模拟载荷位移曲线Fig.10 Test and numerical simulation load displacement curve

4 断裂韧性JC关联模型

分别基于小冲杆试验及标准三点弯试验获得材料断裂韧性JC,并尝试建立二者关联。

4.1 J积分定义

J积分是围绕裂纹尖端,与路径无关的闭合曲线的线积分。图11所示的线弹性或弹塑性平板,开有一穿透切口,围绕其裂纹尖端按逆时针方向做一围线,沿此围线作积分,表示为

(4)

这个积分叫做J积分。

式中,Γ为任意一条逆时针方向绕裂纹尖端的积分回路曲线;W为应变能密度值;Ti为应力分量;ui为位移分量。

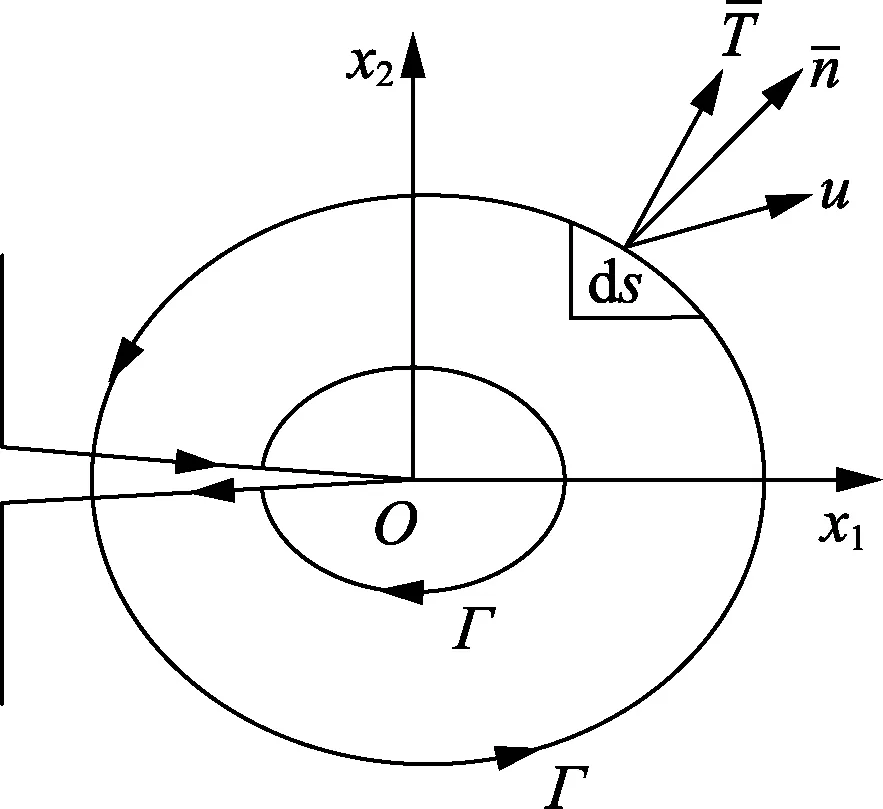
图11 J积分的积分回路Fig.11 Integral loop of J-integral

J积分断裂准则认为当围绕裂纹尖端的J大于等于临界值JC时,裂纹开始扩展,该临界值称之为断裂韧性,常采用三点弯曲试样或紧凑拉伸试样按标准规定的方法测试。

4.2 基于小冲杆试验获取材料断裂韧性JC

采用基于围线积分方法的有限元模型计算环形预制缺口小冲杆试样J积分,该方法要求裂纹保持静态不扩展,因此去除GTN损伤参数,仅利用弹塑性材料参数对试验进行模拟。根据数值模拟结果,剔除非常靠近裂纹尖端和远离裂纹尖端的积分回路[11]。图12为各回路J积分变化曲线。从图12中可以看出,各回路积分曲线重合度高且与积分路径无关,随载荷增加,J积分呈现逐步上升趋势。

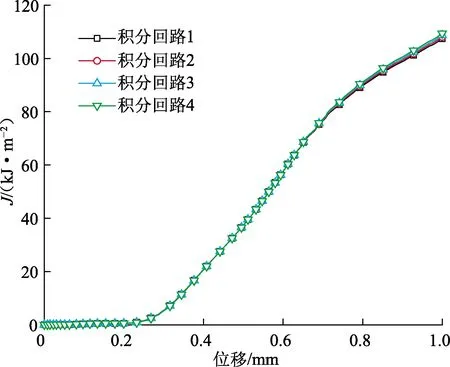
图12 裂纹尖端各回路J积分曲线Fig.12 J integral curve of each circuit at crack tip

获得J积分随位移演化曲线后需要找到起裂点对应的JC值,因此需要确定起裂位移。在小冲杆试验开缺口法求解材料断裂韧性的研究中,许多研究者将载荷位移曲线中的最高载荷作为试样的起裂载荷,与实际情况中不符,实际试样的开裂载荷未达到最高载荷。有鉴于此,本文中使用数值模拟结果来判断试样的起裂位移。当冲头位移达到0.395 mm时,预制缺口尖端出现最大等效塑性应变且发生单元消除现象,如图13所示。因此将0.395 mm作为环形预制缺口小冲杆试样的起裂位移。之后,在图12的曲线中定位位移为0.395 mm时对应的J积分作为小冲杆试验测得的材料断裂韧性JC。4个回路JC分别为20.21、20.18、20.14和20.10 kJ/m2;取4个回路JC的平均值为20.16 kJ/m2。

4.3 基于三点弯试验获取材料断裂韧性JC

为提供材料实际断裂韧性值,按照标准ASTM E1820-2018《Standard Test Method for Measurement of Fracture Toughness》在万能试验机上进行X80管道钢SENB试样三点弯曲试验。在标准三点弯曲试验中,同一材料不同尺寸的SENB试样得到的断裂韧性JC基本一致,可按照实际情况决定试样的尺寸[28]。试样尺寸如图14所示,试样厚度B为10 mm,宽度W=B,裂纹深宽比为0.5,每侧制作深度为0.1B的侧槽。

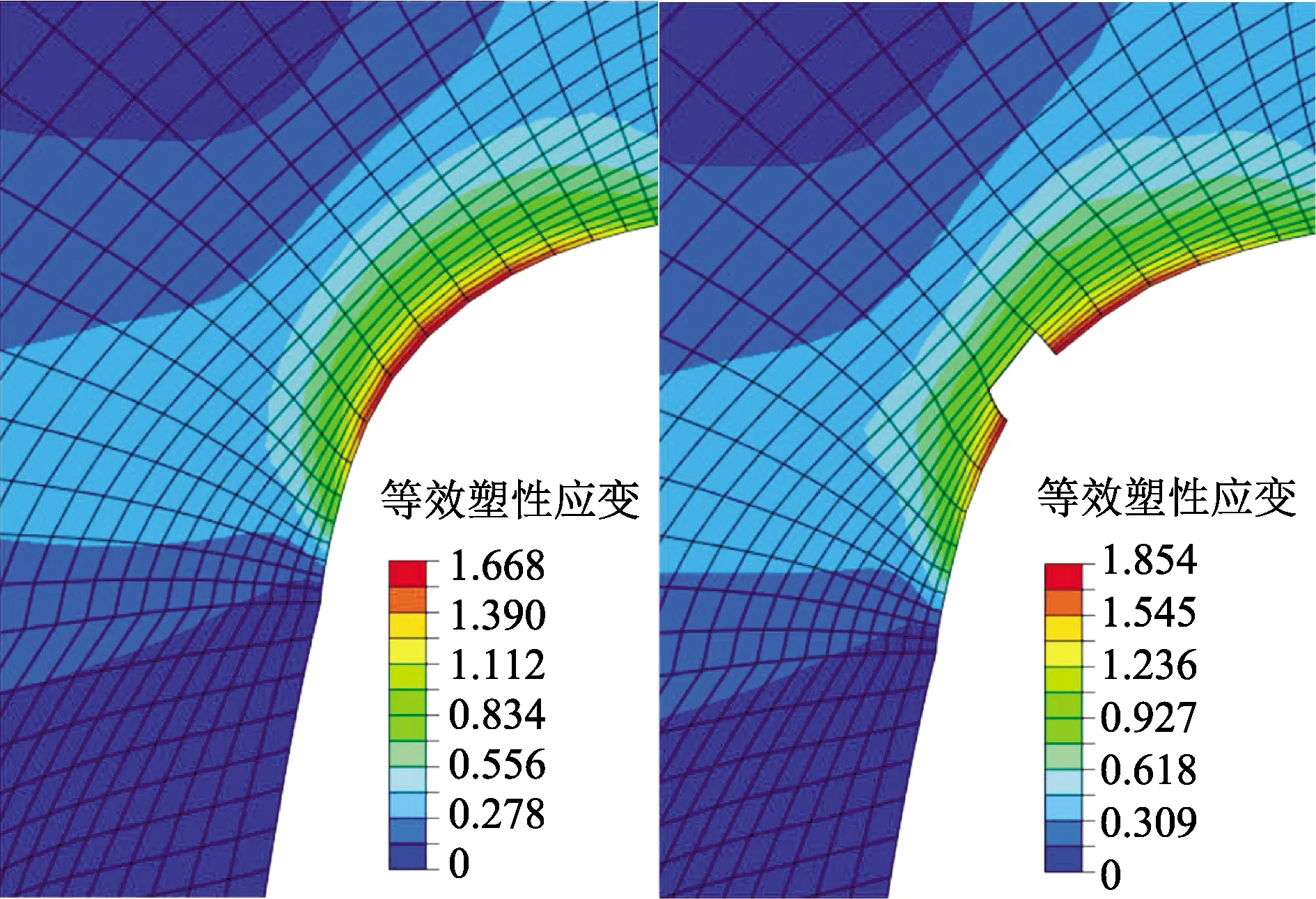
图13 环形缺口试样起裂前后对比Fig.13 Comparison before and after crack initiation of ring notched specimen

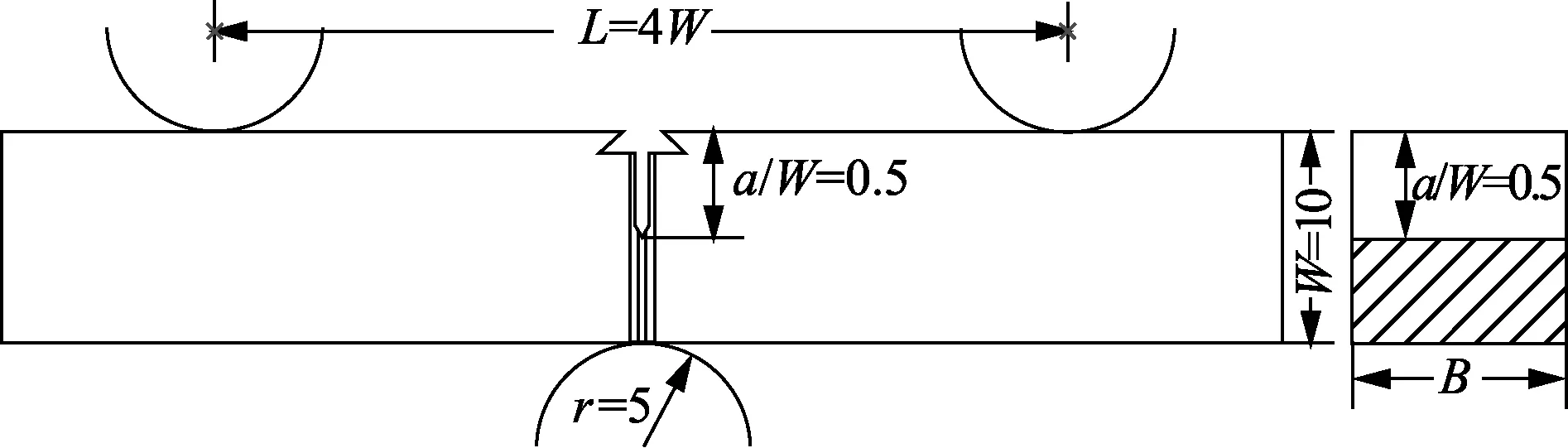
图14 SENB试样示意图Fig.14 Schematic diagram of SENB specimens

采用数字图像相关(digital image correlation,DIC)方法对试验过程进行监测,试验机以0.01 mm/min的恒定位移速率进行加载。试验结束后得到J-R曲线与数据构造线,如图15所示。

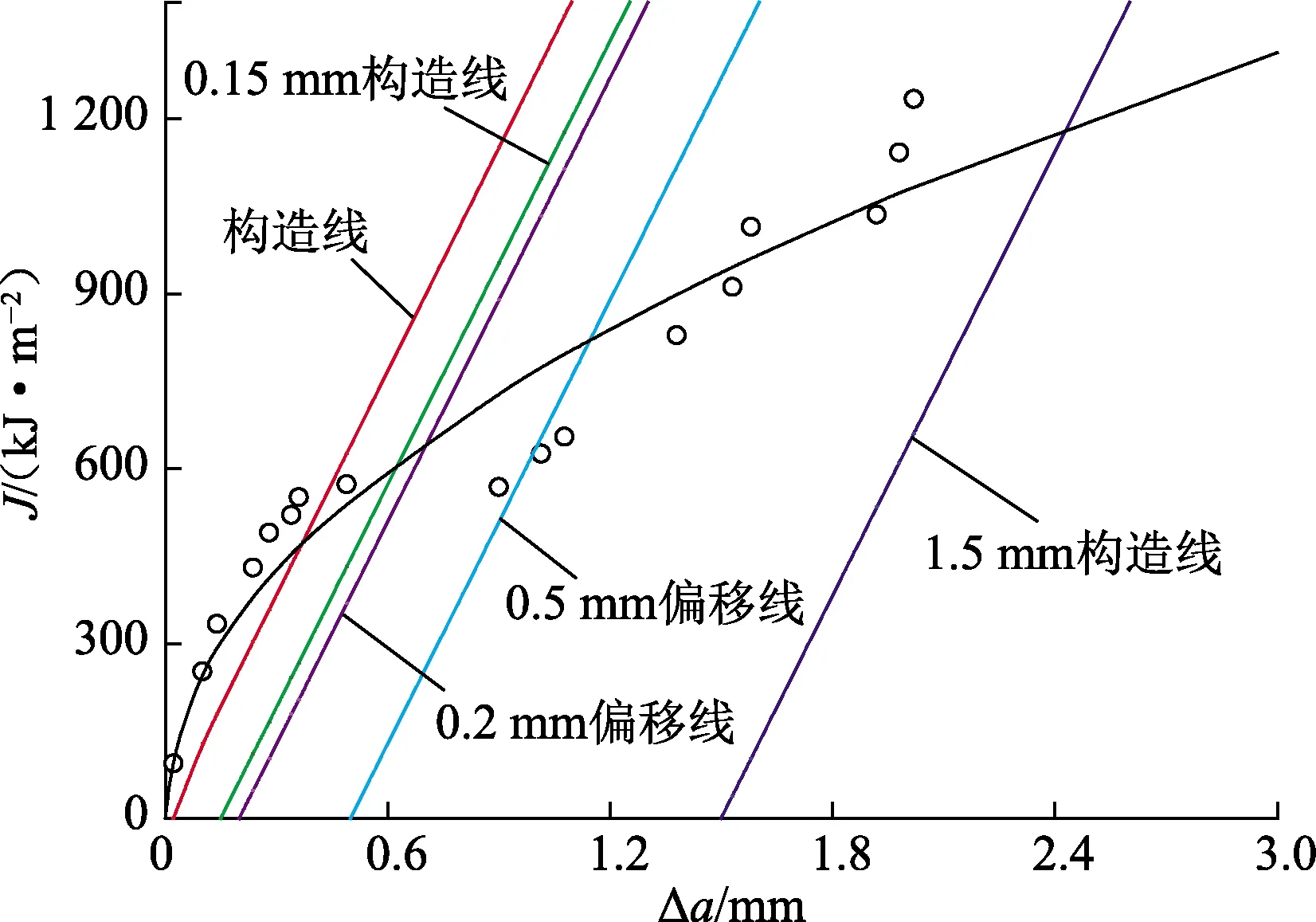
图15 J-R曲线及数据构造线Fig.15 J-R curve and data structure line

对于SENB试样,材料的J积分可由J-R曲线与数据确定用构造线得出,该曲线描述一种测定金属材料断裂韧性JC的单试样技术。由图15可得,0.2 mm偏移线与J积分曲线的交点坐标为(0.701 7,638.26),即材料的断裂韧性JC为638.26 kJ/m2。

4.4 关联模型提出

由环形缺口小冲杆试样得到的X80材料的断裂韧性值(20.16 kJ/m2)远小于常规力学性能测试标准试样得到的断裂韧性值(638.26 kJ/m2),考虑到小冲杆试样尺寸比常规力学性能测试标准试样小很多,存在明显的尺寸效应,微试样的尺寸效应对材料的力学性能测试影响表现在3个方面[29]:①微试样中最小单元的数量较少;②材料的失效模式与试样缺陷及缺陷的生长方向有关;③微试样所受拘束条件与在役结构大尺寸试样相差很大。且二者试件形状与加载模式存在较大差别,可引入比例常数k建立二者所得材料断裂韧性的关系,即

JC=kJC(SP).

(5)

式中,JC为材料标准试件测得实际断裂韧性;JC(SP)为环形预制缺口小冲杆试样得到的材料断裂韧性;k为比例常数。

针对所用X80管道钢材料,确定比例常数k为31.66。可依照上述步骤获得不同材料标准三点弯试验与小冲杆试验所得断裂韧性值的比例常数,并实现二者之间的相互转化,至此建立了基于微损试验确定在役管道材料断裂韧性的方法。