基于机器学习的典型侵财类案件发生概率预测分析方法

卢子涵， 胡啸峰， 侯苗苗

(1.中国人民公安大学信息网络安全学院， 北京 100038;2.安全防范技术与风险评估公安部重点实验室， 北京 102623)

0 引言

我国侵财类犯罪案件数量占比高，破案率低[1]，严重威胁着人民群众的财产安全，乃至影响社会的稳定。在经济迅速发展的新时代，人民群众对公安机关预防、打击侵财类案件提出了更高的要求。抢劫、抢夺和盗窃3类典型侵财类案件具有代表性，根据国家统计局公布的数据显示，仅每年发生的盗窃案数量在刑事案件数量中的占比就能达到60%，长期威胁人民群众的生命财产安全。

李卫红等[2]利用改进的BP神经网络模型建立了侵财类案件预测模型，可挖掘风险要素与案件风险之间的非线性关系；胡啸峰等[3-5]研究了热应力与侵财类案件之间的相关关系，分析了侵财类案件的发生规律；邱凌峰等[6]提出了基于机器学习的社会安全事件预测分析方法，可以预测犯罪人的类型；陈鹏等[7]利用二项逻辑回归算法，以犯罪人的生物、社会和行为信息为特征，实现惯犯身份特征的预测识别；石拓等[8]提出一种基于Bagging和特征选择差异性的集成学习算法进行犯罪预测；杜益虹等[9]构建基于逻辑回归的犯罪概率预测模型，对犯罪信息进行积分预测，按照分数的高低预测犯罪的发生概率。Mehmet Sait Vura等[10]基于朴素贝叶斯理论提出了关于犯罪预测问题的解决方案，提出的模型在预测刑事犯罪的可疑人员方面表现较好。

对典型侵财类案件的发生概率进行预测分析，能够及时有效地预防犯罪的发生。然而当前大多数研究对于侵财类案件的预测分析以盗窃案居多，对抢劫、抢夺类案件的研究极少，并且大多数研究在预测案件发生概率时很少涉及对时间滞后项的考虑，导致执法部门缺乏充足的时间制定防控策略。对典型侵财类案件的发生概率进行预测研究，能够帮助公安机关合理有效地配置警力资源、制定有针对性的巡逻计划，在源头上减少典型侵财类案件的发生。

1 数据及研究方法

1.1 数据集与研究方案

本节选取的数据来源于ZS市2005年2月1日～2015年7月31日的实际典型侵财类案件，以及2005年2月1日～2015年7月31日的实际天气数据。

典型侵财类案件数据集共包含111 579条犯罪数据，经过初步提取后共得到盗窃案件数据66 691条、抢夺案件数据8 608条、抢劫案件数据8 196条。天气数据集共包含19 201条天气数据，每条数据中包含详细的天气情况，一天的天气数据包含不同时间段的测量数据，即每天测量8次或4次的天气数据。

提取的特征通过去除与标签相关性较小的特征等操作后，最后选取的特征包括“时间”“发案概率”“案件总数量”“单类案件总数量”以及从天气数据中提取的“最高气温”“最低气温”“平均气温”“气象站公布当天气象情况”。

“时间”指的是不同时间间隔的时间值，如以1个月为时间间隔，则特征值为“201010”“201011”，以1天为时间间隔则特征值为“20111001”“20111002”；“单类案件数量”指的是在一定的时间长度内某一类案件的发生数量；“案件总数量”是指在与“单类案件数量”相同长度的时间内案件的发生数量；“发案概率”指的是在某一确定时间长度内单类案件数量与所有案件数量的比值；“最高气温”指的是在当天内气温的最高值，一般是在下午2点；“最低气温”指的是在当天内气温的最低值，一般是在凌晨2点；“平均气温”指的是一天中气温的平均值。“气象站公布当天气象情况”指的是气象站在一天中不同时段实时监测的天气情况；“降水量”指的是一定时间长度内降水的平均值。其中，“发案概率”作为预测的标签值，是连续值。

研究方案如图1所示。首先进行提取关键字、处理时间特征等数据处理工作，其次将数据集按照一定的比例随机分为训练集和测试集，运用多种机器学习方法对训练集进行回归分析[11]和交叉验证[12]，然后用测试集进行准确性检验、提出最优模式。

图1 典型侵财类案件发生概率分析研究方案

1.2 数据预处理

首先对一定时间长度下的案件数量进行统计，计算案件发生频率；对每天的最低气温和最高气温进行整理；统计每一天的平均气温；对每一个时间长度中的天气情况进行统计，天气情况经过分类后包括“雷暴”“霾”“晴”“闪电”“无法观测”“雾”“雨”7种情况。最终的样式如表1所示。

表1 数据样式

(1)对天气数据表进行处理时，首先提取“气象站公布当天气象情况”中的关键字。如表2所示，原本在数据集中有25种天气状况，其中有些特征虽然表示的天气状况相同却表述不同，并且过多的特征属性会降低模型的拟合效果。因此，通过提取关键字来统一格式，数据表中的天气状况统一为“雷暴”“霾”“晴”“闪电”“无法观测”“雾”“雨”7种情况。

表2 “气象站公布当天气象情况”关键字提取

(2)插补空白值。“气象站公布当天气象情况”特征中包含有大量的空白值，综合同一个样本内其他特征的值，将空白值填充为“晴”；在“降水量”特征中，将空白值填充为“0”；“最高气温”和“最低气温”两列特征值用当天的最低气温或最高气温填补。

(3)对犯罪数据表进行处理时，首先将天气数据表和犯罪数据表合并。为了减小误差，合并的原则定为：使犯罪数据的时间值和天气数据的时间值最接近。这里需要注意的是，天气数据表在“11.01.2013 23:00”之前是每天测量8次，在“10.01.2013 20:00”之后每天测量4次到6次不等，即犯罪时的天气情况最长误差间隔不超过3小时。

对合并的犯罪、天气数据集进行处理时，按照预设的时间长度对某一类案件数量进行统计，生成特征“单类案件数量”；按照预设的时间长度对所有案件数量进行统计，生成特征“总案件数量”；根据前两个特征的比值，生成特征“发生概率”；按照预设的时间长度统计最高气温生成特征列“最高气温”；按照预设的时间长度统计最低气温，生成特征列“最低气温”；按照预设的时间长度统计平均气温，生成特征列“平均气温”；按照预设的时间长度统计降水量，生成特征列“平均降水量”；按照预设的时间长度统计“气象站公布当天气象情况”特征中不同天气情况的次数。

1.3 机器学习模型

基于前文构建的犯罪数据集和天气数据集，为预测典型侵财类案件的发生概率，本文基于python3.7中开源机器学习模型库Sklearn的岭回归[13]、线性回归[14]、弹性网络回归[15]、支持向量回归[16]以及K最近邻回归[17]共5种机器学习回归模型对典型侵财类案件的发生概率大小进行回归预测，并比较其性能。

2 结果与讨论

本文构建模型时采用的是十折交叉验证法，并用平均绝对误差(MAE)[18]和R2[19]值的大小对模型的性能进行评估。平均绝对误差(MAE)越小，R2值越大代表模型的性能越好。如公式(1)、公式(2)所示。

(1)

(2)

2.1 基于机器学习考虑时间滞后的概率预测

为研究考虑时间滞后的典型侵财类案件发生概率预测方法，以月份为时间长度划分数据集，模型的预测结果如表3所示。

根据表3可知，对盗窃案、抢劫案、抢夺案而言，性能最好的模型均为K最近邻模型，R2值分别为0.83, 0.88和0.8。模型的预测值与真实值的结果比较如图2～4所示。

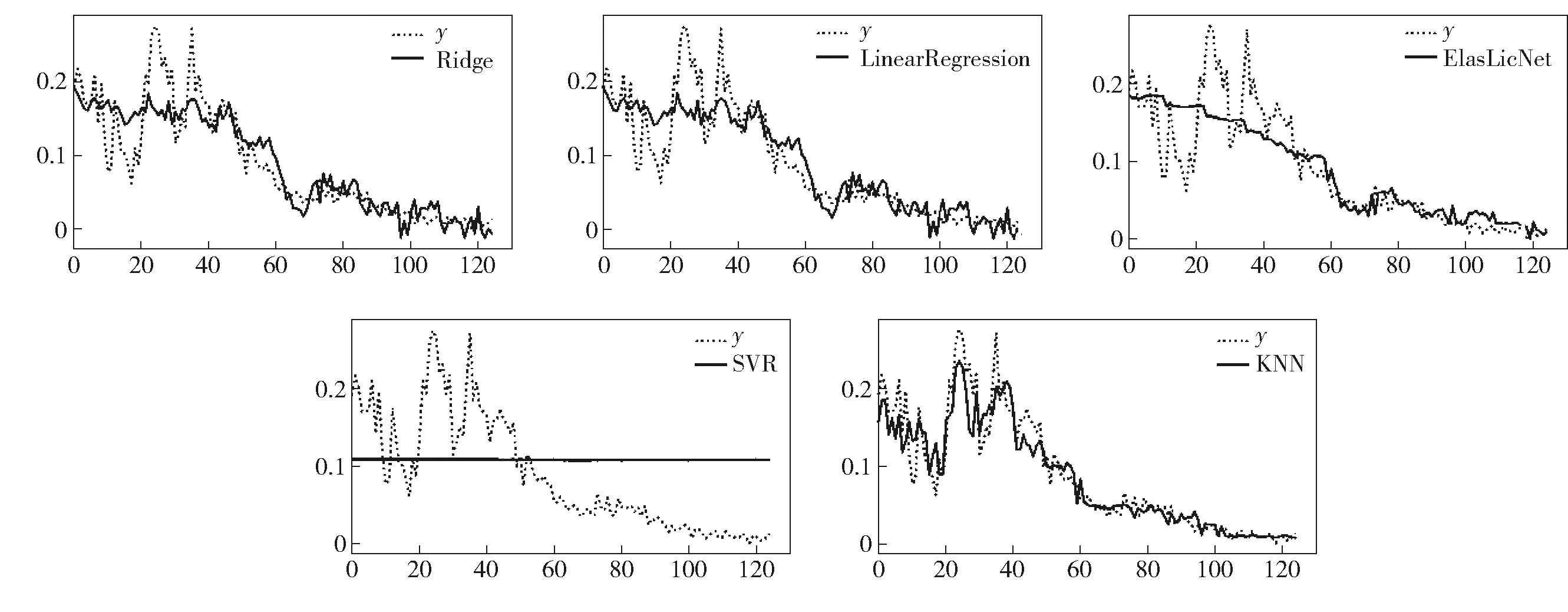
图3 抢劫案件预测值与真实值的结果比较

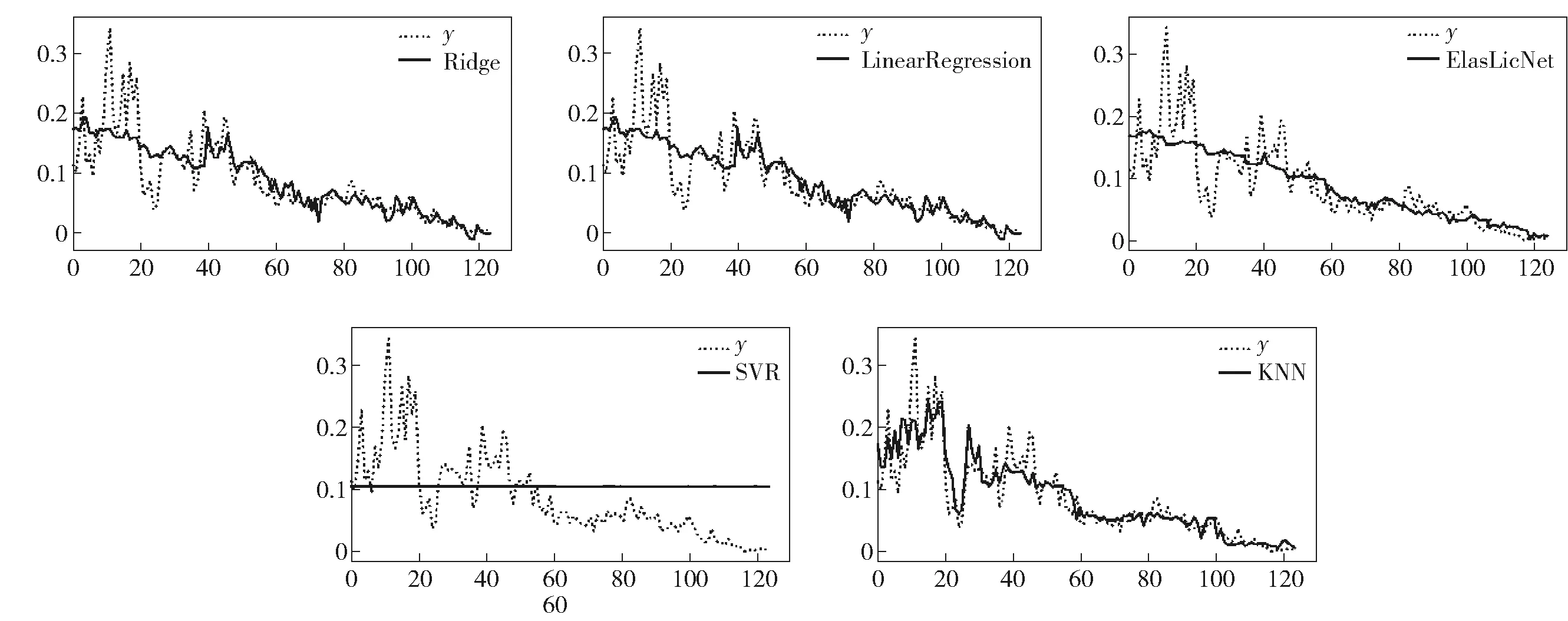
图4 抢夺案件预测值与真实值的结果比较

图中y表示真实值，“Ridge” “Linear Regression” “Elastic Net” “SVR”和“KNN”分别代表模型预测值。

图5所示为盗窃类案件特征的热图分析结果，可见：盗窃类案件中的“单个案件数量”与发案概率的相关性为0.82，“总案件数量”与发案概率的相关性为0.78，即本月的盗窃案件数量或总体案件数量都与下一个月的盗窃案发生概率成正相关，也就是本月盗窃类案件的数量或总体案件数量越多，下一个月的盗窃类案件发生概率越大。

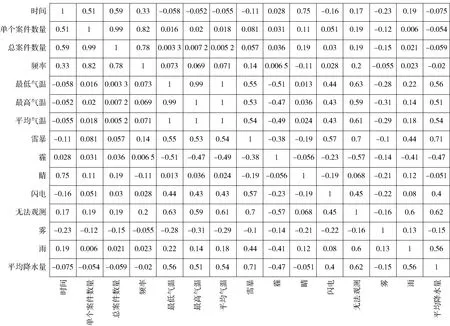
图5 盗窃类案件热图

图6所示为抢劫类案件特征的热图分析结果，可见：

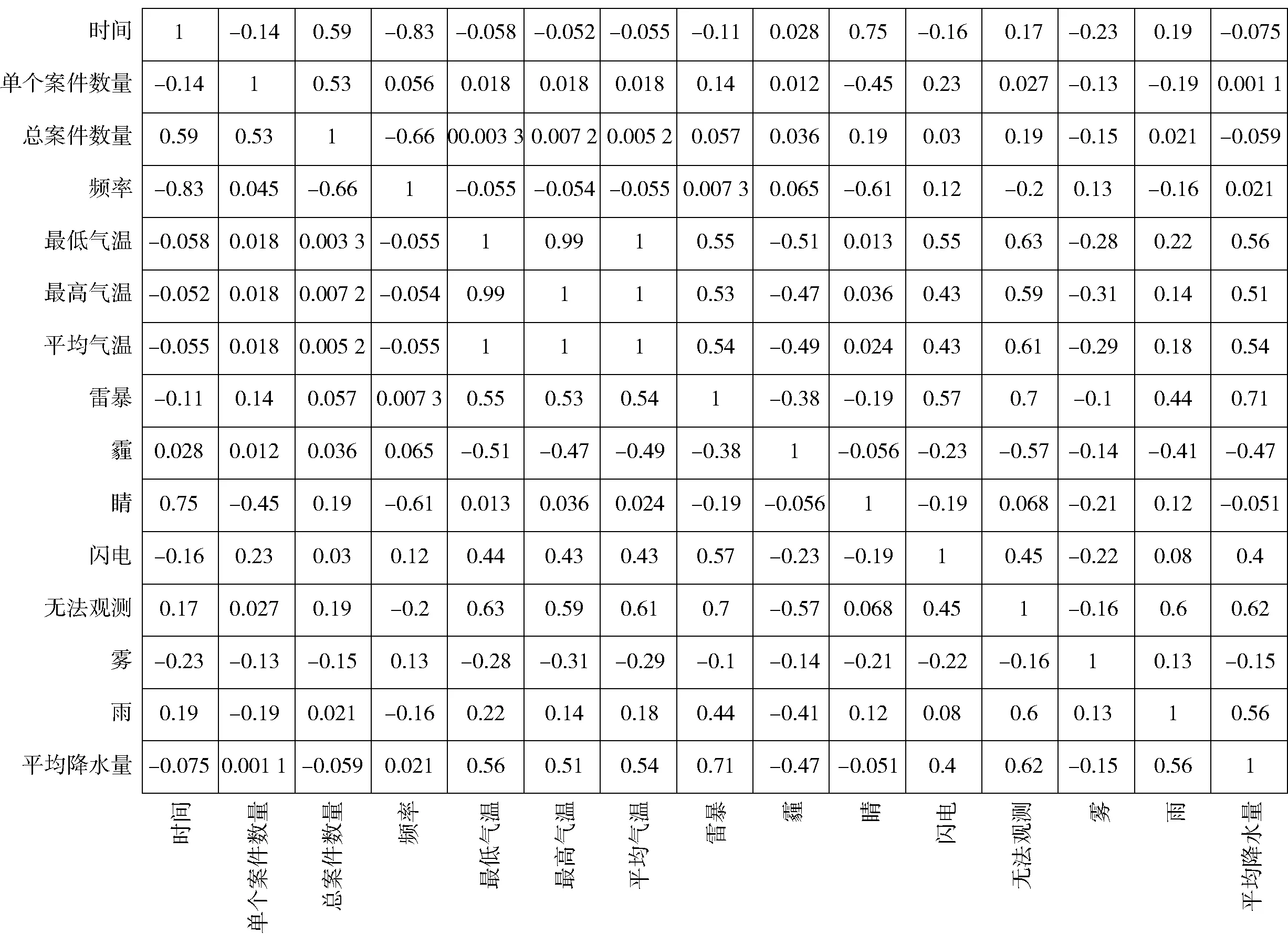
图6 抢劫类案件热图

(1)抢劫类案件的发案概率与“时间”特征的相关性小于-0.8，即抢劫类案件的发案概率和时间成负相关性，也就是随着时间发展抢劫案的发案概率越来越小。

(2)抢劫案件的发生概率与“总案件数量”特征的相关性小于-0.6，即抢劫类案件的发案概率和总案件数量成负相关，也就是上个月中总案件数量越多本月的抢劫类案件发生概率越小。

(3)抢劫类案件的“单个案件数量”和“晴”两个特征的相关性为-0.45，即抢劫类案件的发生数量和一个月中的晴天数量成负相关，也就是本月中晴天数量越多则本月抢劫类案件发生数量越少。

(4)抢劫类案件的发案概率和“晴”特征的相关性为-0.61，即抢劫类案件的发生概率与一个月中的晴天数量呈负相关，也就是本月中晴天数量越多则下个月抢劫类案件发生概率越小。

图7所示为抢夺类案件特征的热图分析结果，可见：

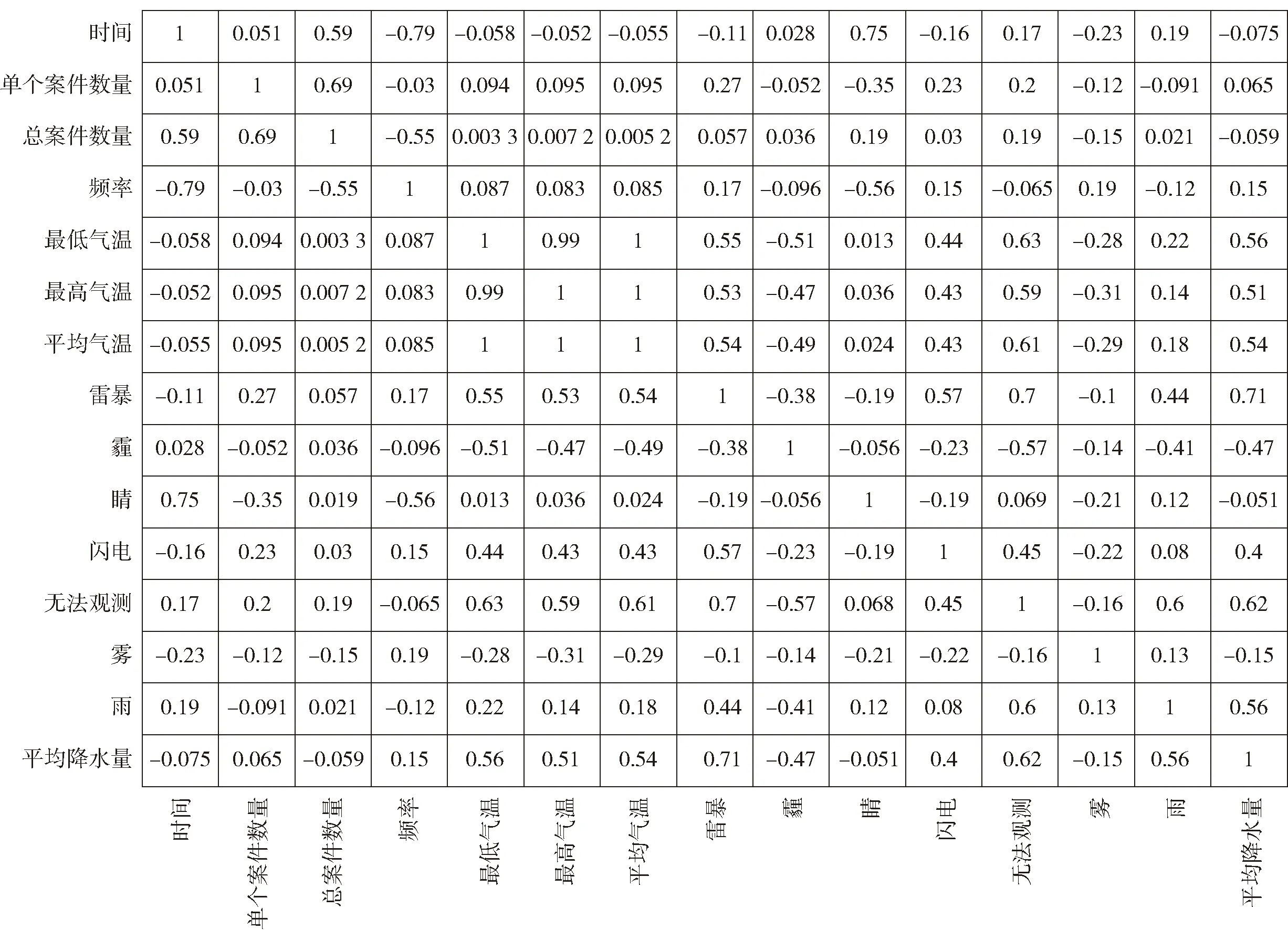
图7 抢夺类案件热图

(1)抢夺类案件的发案概率与“时间”特征的相关性为-0.79，即抢夺类案件的发案概率和时间成负相关性，也就是随着时间发展抢劫案的发案概率越来越小。

(2)抢夺类案件的发生概率与“总案件数量”特征的相关性为-0.55，即抢夺类案件的发案概率和总案件数量成负相关，也就是上个月中总案件数量越多本月的抢夺类案件发生概率越小。

(3)抢夺类案件的发生概率与“晴”特征的相关性为-0.56，即抢夺类案件的发案概率与一个月中的晴天数量呈负相关，也就是说本月中晴天数量越多则下个月抢夺类案件发案概率越小。

2.2 基于机器学习和实时数据的典型侵财类案件发生概率预测分析

在基于机器学习考虑时间滞后的典型侵财类案件发生概率研究中发现，天气状况的统计数量与案件的发生概率有一定的相关性，因此构建基于机器学习和实时犯罪数据、天气数据的典型侵财类案件发生概率预测分析模型。其中，实时的犯罪数据和天气数据都以天为单位。

在2.1的基础上继续进行关键字提取：(1)提取发案地域，将发案地域分为“乡村”“其他区域”“城区”“郊区”和“镇”5个类别。(2)提取派出所的名称，按照派出所的名称划分管辖地域。(3)统计平均风速和平均水平能见度。(4)由于“气象站公布当天气象情况”这一特征在一天的长度中包含多个天气类型，因此将各个特征处理为哑变量。数据样式如表4所示。

表4 数据样式

将处理好的数据带入模型中得到分析结果如表5所示。

根据表5可知，基于实时数据的侵财类案件发生概率预测只有抢夺案的模型泛化性能较好，K最近邻回归模型的R2值能够达到0.7。抢劫案和盗窃案的模型泛化性能不突出，最高分别是K最近邻模型的0.66和0.47。

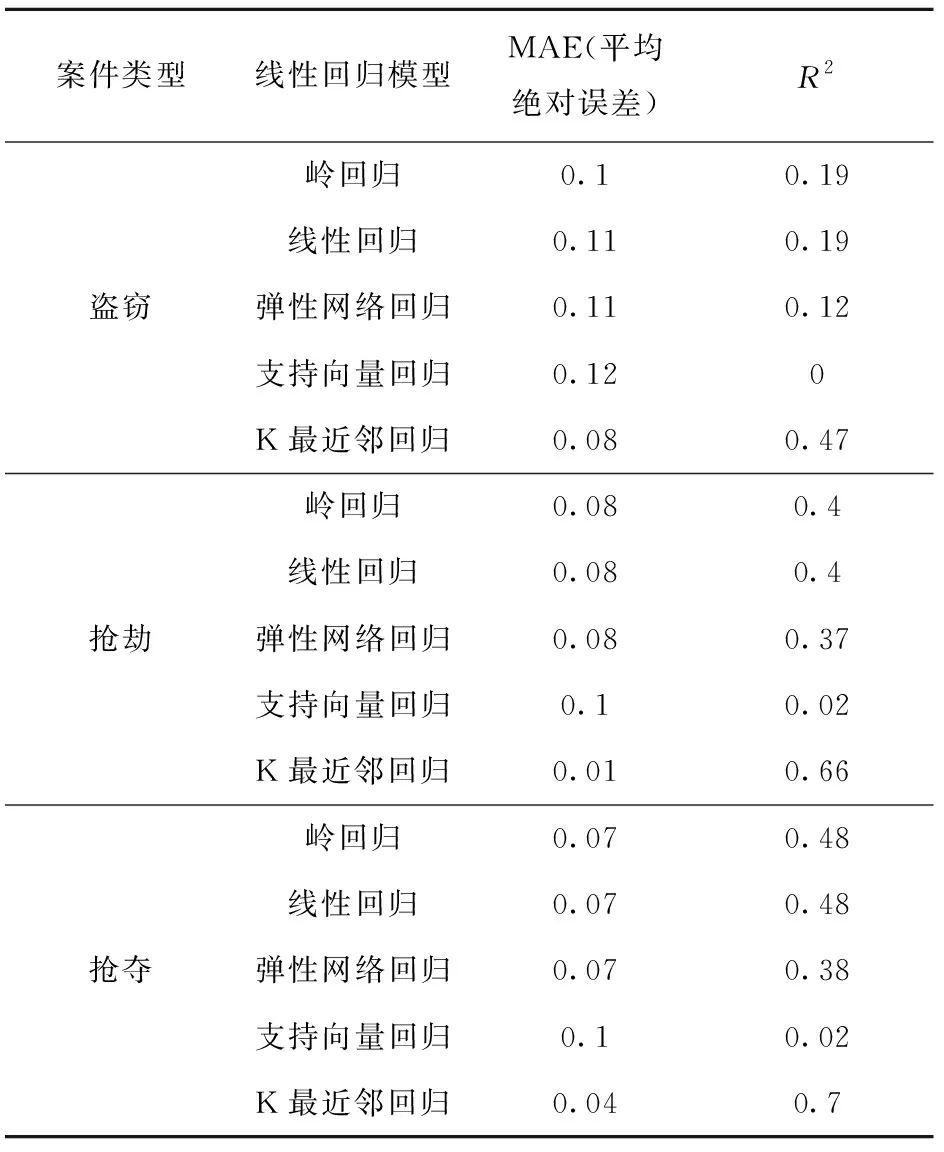
表5 回归模型预测性能评估

3 结论

利用ZS市2005年2月1日～2015年7月31日的实际侵财类案件数据以及2005年2月1日～2015年7月31日的实际天气数据，提出基于时间滞后的预测分析模型。结果显示：盗窃案中，模型性能最好的是K最近邻模型，R2值达到了0.83；抢劫案中，模型性能最好的是K最近邻模型，R2值达到了0.88；抢夺案中，模型表现性能最好的是K最近邻模型，R2值达到了0.8。

提出基于实时数据的线性预测分析模型，利用当天的天气数据及在犯罪前已知的信息建立模型，对典型侵财类案件进行线性分析预测。其中抢夺案的模型泛化性能较好，K最近邻回归模型的R2值达到0.7。抢劫案和盗窃案的模型泛化性能不突出，最高分别是K最近邻模型的0.66和0.47。对线性预测分析结果不好的原因进行了分析：(1)划分的时间段太小时，各个案件的发生均具有偶然性和随机性。(2)数据录入不规范。

本文的研究成果预期可以为执法机关提供预测典型侵财类案件发生概率、内部特征之间相关性的预测分析模型，能够为执法机关的科学决策提供方法依据，为建设综合性的犯罪预测预警系统提供方法支撑。