多维数据库和空间多维数据的数学模型与人工智能
2020-10-27张芮宁
张 阳,张芮宁
(1.中国科学院中科建设 山东东润清洁能源有限公司,山东 东营 257000;2.山东潍坊医学院 临床医学院,山东 潍坊 261000)
空间数据仓库[1]技术是数字地球、数字城市建设中的关键技术之一.随着数据的积累,在达到一定规模时,数据库领域的几种简单数据模型不能满足日益增长的数据需求,很难支持决策服务.为了分析和处理大量的数据,就需要多维数据库的模型来组织数据.在多维数据模型中,数据可以分为两部分:第一部分是决策者要分析的对象,通常称为事实,它包含了一些度量信息;第二部分是决策者分析时的视角,通常称为维度,它包含了关于测量的描述性信息.在实际应用中,由于信息的不完全性和不精确性,很难完全划分出清晰的不相交边界.针对这些问题,特构建出空间多维模型,即在雪花模型中引入空间距离,从而构造出空间多维数据模型和空间立方体.人们总是希望把各种复杂空间数据所取得的多维数据表示在一张图上,以期从中找出规律和发现问题.因为图形表示具有明显直观的特点,所以它是帮助人们思维和判断的重要手段.特别在多元统计中,多维数据的图形表示法起着极重要的作用.过去常用平面图、剖面图和三角图示法来表示两两变量和最多三个变量的关系,而对大于三个变量的表示,几乎不可能做到.为此,如何用简化的逻辑数学公式表示各种空间多维数据结构拓扑图是人们长期以来所探讨的一个研究课题.
一般认为,人工智能网络是模仿人脑结构功能而制成的信息处理系统,可以应用于信号处理、模式识别、知识工程、专家系统、调校组合、机器人控制等领域.但随着科技发展,海量的数据处理需求使数据库和空间多维数据处理能力面临严峻挑战.从脑科学的角度看,人工智能与大数据、区块链、云计算[2-5]、工业互联网之间的关系,可以衍生各种复杂数据计算,但是大体量的数据拓扑图线路繁杂不便于观察[6-10],这些数据的内容,包括数量、速度、多样性等也呈现了不断增长的复杂性,而网络图的数学模型[11-15]可以给数据库和空间多维数据计算提供清晰的逻辑关系,故建立数据库和空间多维数据架构数学模型就显得尤为重要.本文运用雪花结构分支分层将数据库和空间多维数据架构成数学模型,将实际事物中错综复杂而又难以解决的因素进行层次降解,形成一个有序的分支层次结构.通过数学模型将数据库和空间多维数据复杂的数据转化为简单化逻辑化的数学公式来表示,并使数据库和空间多维数据人工智能化.其特别适合计算机架构师、需经常上课画网络图的教师、各种管理组织者、科研工作者及规划设计等人员,并可应用于数据降维[16]、人脸识别、3D识别、多维计算、机器人控制、无人驾驶、人才选拔测评[17]、招聘人才测评等各种定性定量难以确定的工作.
1 多维数据库和空间多维数据的数学模型与求解
1.1 多维数据库的数学模型建立
在多维数据库里,多维数据模型的逻辑结构可用星型模式表示.星型模式的核心是一个事实表,围绕它的是维表.它们的关系如图1所示.
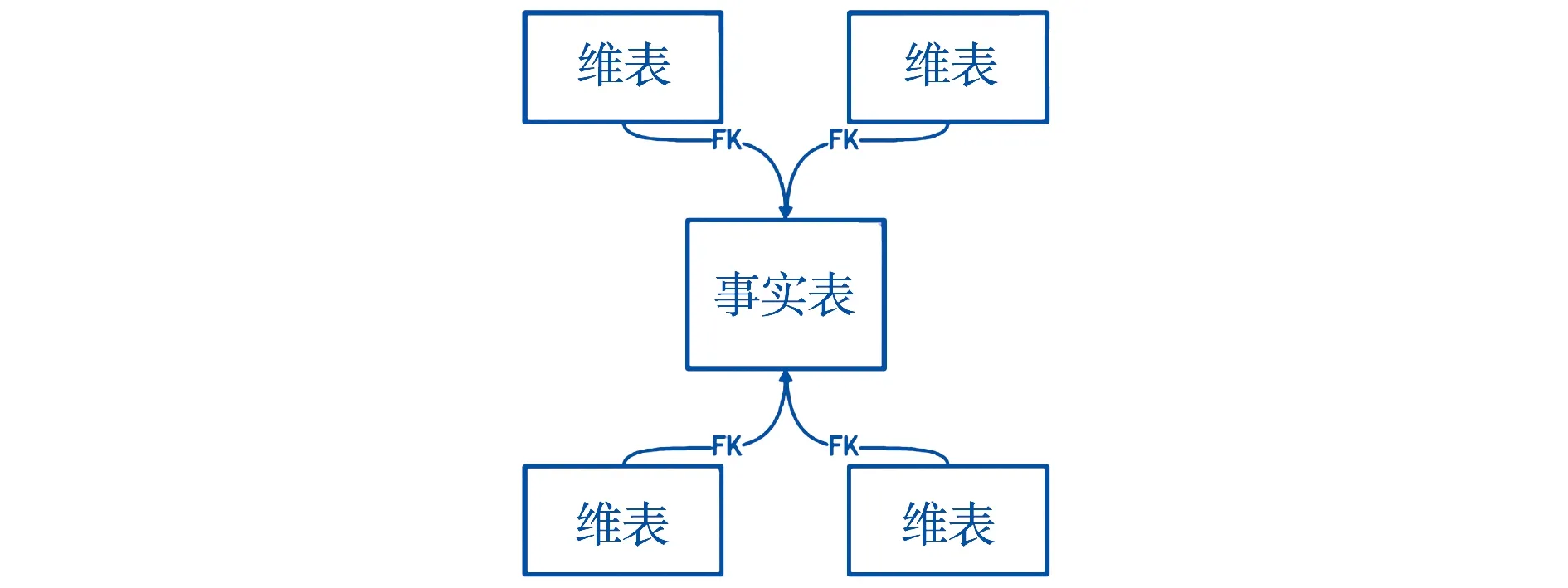
图1 星型模式
将多维数据库星型模式变成星型数学模型如图2所示.
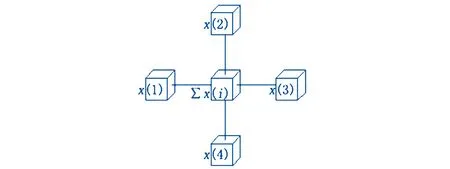
图2 一层多维数据库星型数学模型
得到一层多维数据库星型数学模型:
(1)
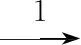
对于复杂的多维数据维模型来说,星型模式并不够理想.因为很大的维表对性能是不利的,部分地抵消了聚集数据得到的性能.在某些情况下,存蓄维元素的属性将耗费大量空间,当维元素很多时,表现将更为突出.将星型模式进行拓展,可得到雪花模式如图3所示.
依据图3建立一个多维数据库雪花模式拓扑逻辑数学模型如图4所示.
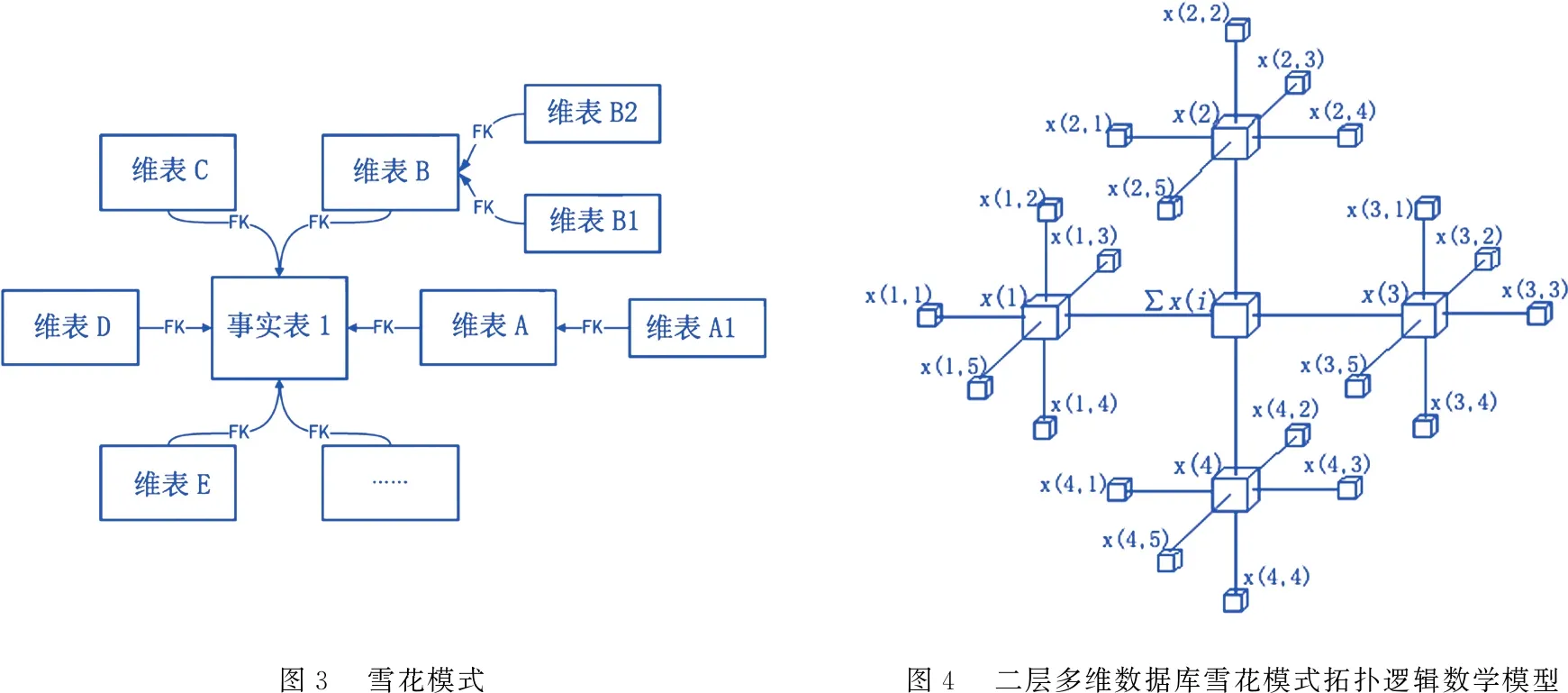
图3 雪花模式图4 二层多维数据库雪花模式拓扑逻辑数学模型
图4对应的多维数据库数学模型为
由上式推导出2层多维数据模型数学公式为
(2)
由此可推出n层多维数据库数学公式为
(3)
公式中:(i,…,i)为n层所有集数.
由公式(3)推导全架构多维数据库数学公式为
(4)
此公式可反向表述即
雪花模式可使性能提高并节省磁盘存储,对于表有很多行、许多属性存储在低级别的维等级表中或磁盘容量有限的情况,雪花模式是有效的.
1.2 空间多维数据的数学模型
我们的宇宙空间合起来只有一个,几维空间就是我们用几个相互关联的变量来描述这个空间.当我们用眼睛去看世界时,我们直观地确定一个物体某一点的空间位置可以用三个参数,只是三维;如果这个物体的位置是个变量,为了描述此物体前后位移,那么我们还应引进第四个参数时间,这就是四维;如果这个物体的大小是个变量,我们还引进长宽高甚至跟多的东西.其实四维五维甚至更多的维度都只是数学公式里面的东西,四维就是公式里有四个参数,五维就是公式里有五个参数,以此类推六维七维就可想而知了.如果这些参数遵循一定的规律,我们可以将这一规律总结成一条公式,我们通过这条拥有几个变量的公式来描述这个空间的物体,可以理解为我们用几维的思想来认识这个世界,我们看到了几维空间.维数越多,我们对世界的描述认识也就越精确.
数据仓库是在企业管理和决策中面向主题的、完整的、非易失的、不同时间的、用于支持决策管理的数据集合,采用传统的多维数据模型和OLAP技术处理空间数据具有较大的局限性,针对这些问题,特构建空间多维模型.即,在雪花模型中引入空间距离,从而构造出空间多维数据模型和空间立方体.一个空间多维数据数学模型图,如图5所示.

图5 空间多维数据拓扑逻辑数学图
由上图得到空间多维数据的数学模型为
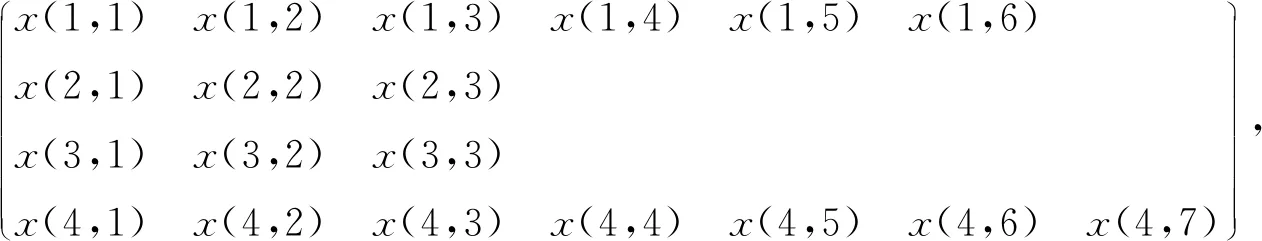
得到一层空间多维数据的数学模型为
(5)
同理,二层空间多维数据的数学模型为
(6)
由此可推出n层空间多维数据数学模型公式为:
(7)
由公式(5)~公式(7)推导全架构空间多维数据数学公式为:
(8)
由公式(8)得到如下球体空间多维数据立方体内部剖面图,如图6所示.
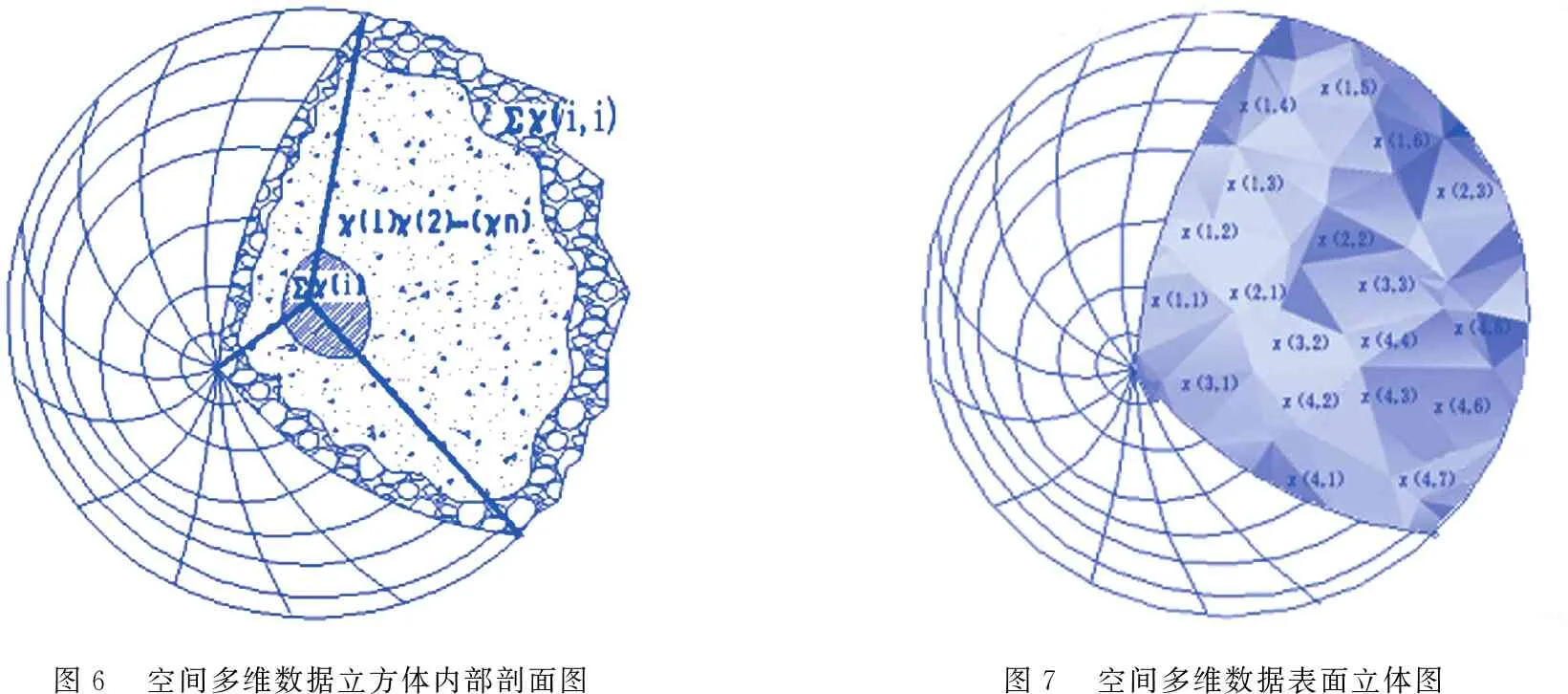
图6 空间多维数据立方体内部剖面图图7 空间多维数据表面立体图
由公式(8)得到如下球体空间多维数据表面立体图,如图7所示.
1.2 多维数据库及空间多维数据的数学模型的分解合并公式
多维数据库经常出现需要精简维表或需要增加维表,单层多维数据库维表发生减少的拓扑图,如图8所示.

图8 单层多维数据库维表减少拓扑逻辑图
多维数据库减少一个维表公式为
公式中:∑y(i) (i=1,2,…,n)为多维数据库变化后新维表的集合.
对应的,单层多维数据库增加一个维表推导的网络模型结果为
同理,可推导多层多维数据库的分解和合并模型为
(9)
公式中:(k=1,2,…,n)为所有层可增减多维数据库集数.
同理,由多维数据库的分解和合并模型公式可推导空间多维数据的分解和合并模型公式
(10)
1.3 多维数据库和空间多维数据模型运转效率数学公式
多维数据库运转效率用比率V来表示,又称多维数据库缩放比,可建立一个单层缩放比公式,如图8、图9所示.
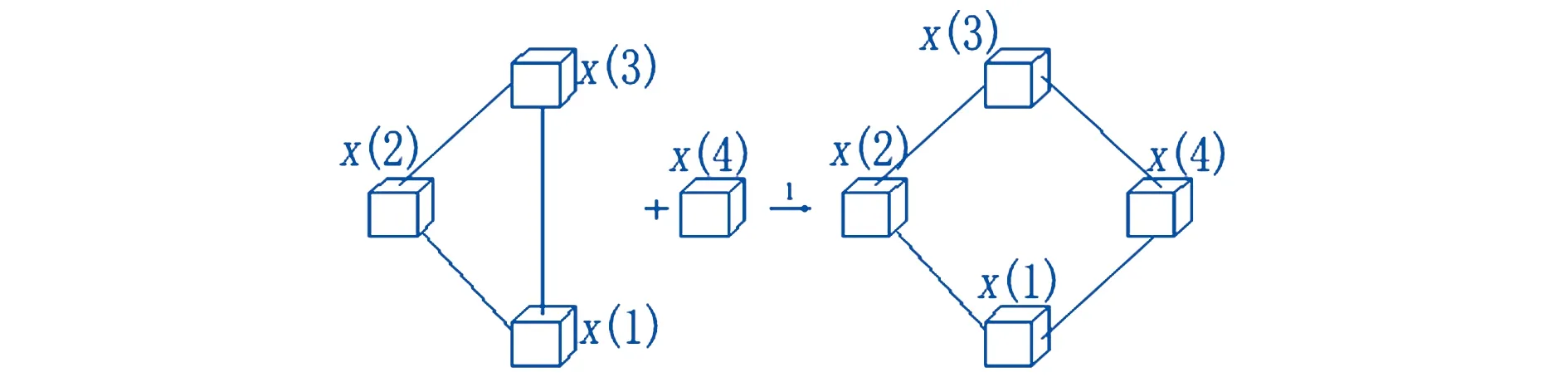
图9 单层多维数据库维表增加拓扑逻辑图
n层多维数据库的缩放比公式为
(11)
由多维数据库的缩放比公式可推导空间多维数据的缩放比公式为
(12)
从缩放比公式可知,缩放比值越大多维数据库和空间多维数据运转效率越高,反之亦然.将多维数据库和空间多维数据运转效率公式运用数据网络上会变成多维数据库和空间多维数据实时动态图.
1.4 多维数据库和空间多维数据数学模型数学逻辑地址
多维数据库和空间多维数据的存储地址现存的寻址方法是比较复杂的.主要有两种,一种是以行为主序的顺序存储,另一种是以列为主序的顺序存储,这两种的排序都很复杂且数据编排不便表示.用多维数据库和空间多维数据数学模型表示数学逻辑地址,比较清晰简洁.我们把维表用数学逻辑地址表示.
如图4,维表x(2,3)数学逻辑表示式为
多维数据库数学逻辑地址公式为
(13)
在空间多维数据中维表x(4,7)数学逻辑表示为(见图5):
空间多维数据数学逻辑地址公式为
(14)
本多维数据库和空间多维数据的数学逻辑地址特点是表示简单,可以无限扩充.
例如:无人驾驶汽车驾驶到某地方点的空间数学逻辑地址,高程为754 m,时间为北京时间9点10分,北斗卫星定位坐标为3 453 798;1 328 923.可以表示这个点的地址为
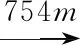
从上面空间多维数据数学逻辑地址看空间位置是四维空间,一个高程、一个时间、一个纵向位置、一个横向位置.
1.5 多维数据库和空间多维数据数学模型的乘法推导公式
由多维数据库的数学模型加减法推导出多维数据库数学模型乘法公式为
(15)
由空间多维数据的数学模型加减法推导出空间多维数据数学模型乘法公式为
(16)
注:多维数据库和空间数据模型数学模型加减法及乘法为与对应原数学模型相加减乘.
1.5 多维数据库和空间数据数学模型的特征向量和特征值
先来回顾下我们所熟知的特征向量和特征值.若是存在一个矩阵A,让这个向量v在线性变换后,方向仍然保持不变,只是拉伸或者压缩一定倍数,即:Av=λv.那么,这个向量v就是特征向量,λ就是特征值.特征向量和特征值的几何本质,其实就是空间矢量的旋转和缩放.
由于多维数据库和空间多维数据数学模型乘法公式就是网络的空间缩放,公式(15)、公式(16)具有特征向量与特征值性质,所以特征值λk=∑x(k,…,k).即多维数据库数学模型乘法公式变为
(17)
将公式(15)、公式(17)代入特征向量与特征公式得
(18)
同理,空间多维数据特征向量与特征值公式为
(19)
1.6 机器学习网络数学模型
人工智能网络[18]是由大量神经元按照大规模并行的方式通过一定的拓扑结构连接而成的网络.目前使用最广泛的是(BP)神经网络和它的变化形式,它由输入层中间层(隐含层)和输出层组成,具有三层或三层以上的阶层神经网络,相邻层之间的神经元全互联,同一层内的神经元无连接.BP网络模型如图4所示.

图10 BP神经网络结构图
图4BP人工智能神经网络数学模型代入公式(4)简化为
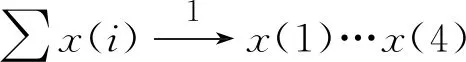
推导出BP人工智能神经网络数学模型公式为
(20)
小结:BP人工智能神经网络在数据库和空间数据加密编码及优化数据运算方面可提高效率.
1.7 深度学习多维数据库和空间多维数据的数学模型
让计算机能够自动的从数据中“学习”规律,并利用规律对未知数据进行预测,这是计算机模拟或实现人类的学习行为,用以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能.通过从数据里提取规则或模式来把数据转换成信息,数据首先被预处理,形成特征,然后根据特征创建某种模型,之后将收集到的数据,分配权重、偏置和其他参数以达到学习目的.
整个神经网络的计算可以用矩阵式给出.我们给出神经网络单层的式子.每层的神经元个数不一样,输入输出维度也就不一样,计算式中的矩阵和向量的行列数也就不一样,但形式是一致的.假设我们考虑的这一层是第i层.它接受m个输入,那么这一层的计算如下式所示:
(21)
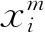
从多维数据库数学模型的特征向量和特征值公式(17)代入公式(21)得到多维数据库深度学习数学模型为
(22)
由公式(4)代入公式(22)推导多维数据库深度学习全架构公式

(23)
同理,推理得到空间多维数据深度学习数学模型
(24)
空间多维数据深度学习全架构公式

(25)
综上所述,多维数据库和空间多维数据深度学习数学模型是将原数学模型变换了一种形式,使模型更简单化,数学表述更图像化,逻辑关系更清晰化.此模型的优点是:
①清晰明确的逻辑关系,用数学公式表示的方法简单方便;
②用分支分层的方法,把各个分支和各层数据一一列出并进行计算,条理清楚,定性准确,定量分析的结果符合实际要求;
③成本低、效率高、可操作性强并且计算量低.
3 结 语
将事物用逻辑数学公式表示出来是人类科技工作者的永恒梦想.本文在已有的多维数据库和空间多维数据拓扑图上建立新的架构数学模型,将原拓扑图用抽象化数学公式来表示,简化了拓扑图繁琐复杂的各种线段及空间点的表示方法,公式简单明了,并可将公式展开为原多维数据库和空间多维数据拓扑图.通过简单的数学公式节省了画图时间,逻辑关系清晰,而且便于分析和计算多维数据库和空间多维数据点或线及面的各种数据,特别是像大数据、云计算等复杂数据的分析和计算.其具有成本低、效率高、可操作性强且计算量低等优点.多维数据库和空间多维数据数学模型可以使用的结构是星型结构、环型结构、树型结构、网状结构和混合结构等;数学公式可以用矩阵计算各种分析的结果并用软件快速出数据,还可以变成动态的数据图,从而反映数据的实时运行情况.从使用性方面来说,多维数据库和空间多维数据数学模型也可生成新的数据模型,还可解决各种条件下数据各单位的排序问题,其可加密数据的特点,又可以优化数据并满足数据拓扑管理的要求,从而便于数据的分级管理.以上就形成了一个比较系统、全面的人工智能多维数据库和空间多维数据数学模型分析体系.
