考虑壁面滑移效应的充填料浆管道输送阻力研究

2020-10-26甘德清闫泽鹏薛振林刘志义孙海宽

金属矿山 2020年9期

甘德清闫泽鹏薛振林刘志义孙海宽

（1.华北理工大学矿业工程学院，河北唐山063200；2.河北省矿业开发与安全技术重点实验室，河北唐山063009）

近年来，浅部矿产资源逐渐减少，导致矿山开采深度不断增加，伴随而来的“三高”（高温、高压、高井深）问题日趋严重［1］。充填采矿法的有效应用有助于解决深部采场的高地应力问题，并以其绿色、环保、安全等特点，逐渐成为地下矿山的主要开采方法［2-3］。与其他充填方法相比，高浓度全尾砂充填工艺具有成本低、易于实现机械化的优点［4］。管道输送是高浓度全尾砂充填工艺的关键环节，是确保系统稳定、高效运行的前提［5］。管道输送过程中常发生堵管、磨损等事故，限制了充填矿山的生产能力，有研究认为管道阻力是影响充填管道稳定性及管路堵塞的主要原因［6］。

影响管道输送阻力的因素众多，由于受到测量手段和试验装置限制，常规的环管试验受到多种条件制约，粗略的测量值很难作为论证依据［7］。随着计算机技术的发展，数值模拟（数值计算）成为研究流体流动的重要手段［8］。甘德清等［9］通过Fluent软件模拟得出料浆管道阻力损失与管径呈反比。温震江等［10］通过模拟验证得出，相同浓度时管道阻力损失与流量呈正相关。杨波等［11］通过ANSYS/FLOTRAN模拟料浆在充填管道内的流动特征，得出入口速度增大时，浓度对管道阻力的影响极小。谢翠丽等［12］应用Fluent软件对煤水两相流动过程中的表观滑移现象进行了研究，发现固相体积分数较低时，出现超前滑移现象。

由于高浓度料浆属于非牛顿体范畴，因而其在管道输送过程中必然存在表观滑移现象［13］，忽略壁面滑移效应对管道阻力损失的影响得出的模拟结果，与充填料浆管道输送的实际情况会有一定的偏差。为此，本研究基于Comsol软件建立考虑壁面滑移效应的管道输送数值模型，分析管径、灰砂比及浓度对管道输送阻力的影响规律，并以某矿山为例，给出最佳的充填管路技术参数。

1 数学模型

1.1 模型假设

管道内部主流区与滑移层接触部分的流体速度分布是连续的，壁面滑移速度是剪切流动区和滑移层连接处的速度与管道内壁的速度差［14］。为便于分析，本研究对浆体在管内的流动行为进行假设：①管道内的流体为均质体，滑移层内流体在输送管道内各区域滑移层厚度相同；②管道输送过程中不存在热交换；③滑移层的状态不会影响主流区的浆体。

1.2 理论模型

（1）滑移流动的基本方程。根据管流中剪切速率的定义γ=4vR及管流基本公式，得出管径为R的管道中料浆产生壁滑移时的基本流动方程［15］为

式中，R为管道半径，m；v为浆体平均流速，m/s；τ为壁面剪切应力，Pa；τw为临界剪切应力，Pa；vslip为壁面滑移速度，m/s。

（2）黏性耗散。管道输送过程存在的黏性耗散量是一个与速度梯度相关的物理量，可表示为

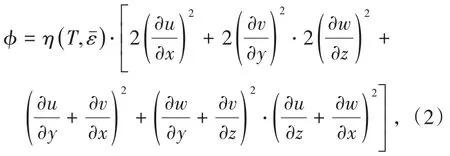
式中，φ为黏性耗散量；η为流体黏度，Pa/s；u、v、w分别为X、Y、Z轴方向的速度分量，m/s；T为料浆温度，℃为耗散率平均值，%。

1.3 控制方程

对于不可压缩的流体，Comsol软件中控制流体流动的基本方程主要有能量守恒方程、质量方程和状态方程，控制流动的变量有流体压力P、密度ρ、温度T和流速u。

Navier-Stokes动量守恒方程（忽略外部体积力）可表示为

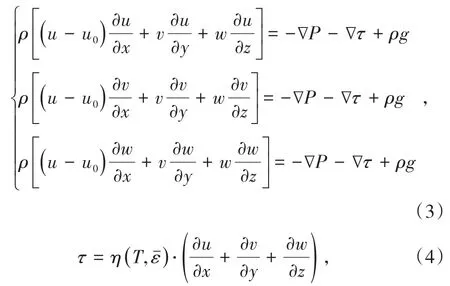
式中，u0为料浆初始速度，m/s；ρ为料浆密度，kg/m3；g为重力加速度，9.8 m2/s；u、v、w分别为X、Y、Z轴的3个速度分量，m/s。

质量守恒方程可表示为

式中，ρ为料浆密度，kg/m3；u为料浆速度，m/s；t为料浆输送时间，s。

状态方程可表示为

式中，ρ为料浆密度，kg/m3；P为流体压力，Pa；T为温度，℃。

2 模拟试验设计

2.1 试验材料

本研究全尾砂样品取自河北某矿选矿厂，从底堆处取料，经烘干后备用测定其密度为2 850 kg/m3。采用激光粒度仪对尾砂颗粒的粒级组成进行测定，得到其中位粒度d60=17.53 μm。根据矿山充填开采经验，以325#矿渣硅酸盐水泥为胶凝剂，经测定其密度为3 080 kg/m3。

2.2 方案设计

根据国内矿山自流充填系统的发展情况［16］，选择充填管路倍线5，管径为100 mm、150 mm和200 mm。为了更加科学合理地得到试验数据，同时尽可能减小试验工作量，以灰砂比、料浆浓度及管径为主要影响因素设计了考虑三因素三水平的正交试验，试验参数取值如表1所示。

根据雷诺数Re计算公式［17］，分别计算了不同条件下的雷诺数，发现雷诺数均小于2 300时，管内流动状态属于层流。设定边界条件“入口—充分发展的流动—平均速度—2 m/s”；Z方向设置重力为体积力；由于设置重力为体积力，设置管道出口边界条件为0或层流流出会导致模拟计算不收敛，需要设置出口为“开放边界”且无黏滞应力并加入压力积分为0的约束；设置壁面条件为滑移速度（介于无滑移和滑移之间可以较好地表征壁面滑移效应）。

2.3 几何模型建立及网格剖分

本研究基于Comsol软件三维空间维度对充填管路进行建模，弯管曲率半径为0.5 m，由于充填倍线为5，设置竖直管长度为1.5 m，水平管长度为9.5 m。Comsol软件自带的网格剖分工具有很强的编辑能力，用户可根据需求调整网格的形状、大小等。考虑到滑移层极薄，为使计算结果更精确，设置模型的边界层数为5，边界层拉伸因子为2，最终剖分单元数目为350 623。建模效果如图1所示。

3 数值模型可靠性验证与结果分析

3.1 壁面滑移数值模型可靠性验证

吴爱祥等［18］经物理试验研究，提出的壁面滑移作用下的管道阻力公式为

式中，ΔP为管道压力损失，Pa；D和L分别为管道直径和管道长度，m；μp为高浓度料浆黏度，Pa/s；τy为料浆屈服应力，N；δ为滑移层厚度，取δ=5 μm；μslip为滑移层黏度（黏度极低将其看作常温状态下的水，取μslip=1.05 mPa·s）。

文献［19］提出的管道阻力损失计算的常用公式如下

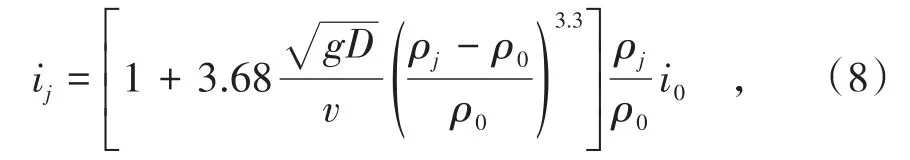
式中，ij为充填料浆水力坡度，mH2O/m；i0为清水水力坡度，mH2O/m；g为重力加速度，9.8 m2/s；D为管道直径，m；v为料浆流速，m/s；ρj和ρ0分别为料浆和清水的密度，kg/m3。

为验证Comsol数值模型在充填料浆管道输送阻力损失研究方面的可靠性，将上述试验条件代入式（7）和式（8）进行计算，对比分析数值模拟结果和公式计算结果，如表2所示。

由表2可知：式（8）计算结果与数值模型的计算结果相对误差为48.1%～386.1%，误差极大。原因是该式在多次试验的基础上所得，试验条件对公式的适用性影响较大，且该式未考虑壁面滑移对管内料浆流动的影响；式（7）计算结果与数值模拟计算结果的相对误差在20%以内，说明本研究试验所建立的考虑壁面滑移效应的数值模型相对可靠。

3.2 数值模拟结果分析

将数值模拟数据导入DPS数据处理软件中，采用极差分析法研究料浆浓度、灰砂比、管径对阻力损失的影响程度，并建立了阻力损失关于三者的回归方程。试验结果如表3所示。

由表3可知：考虑壁面滑移效应时，各因素对管道阻力的影响程度依次为管径＞质量浓度＞灰砂比。通过回归拟合建立的阻力损失与浓度、灰砂比、管径的函数关系式为

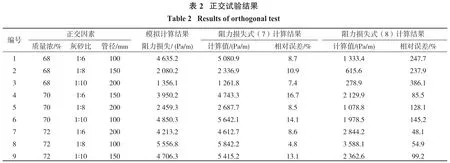
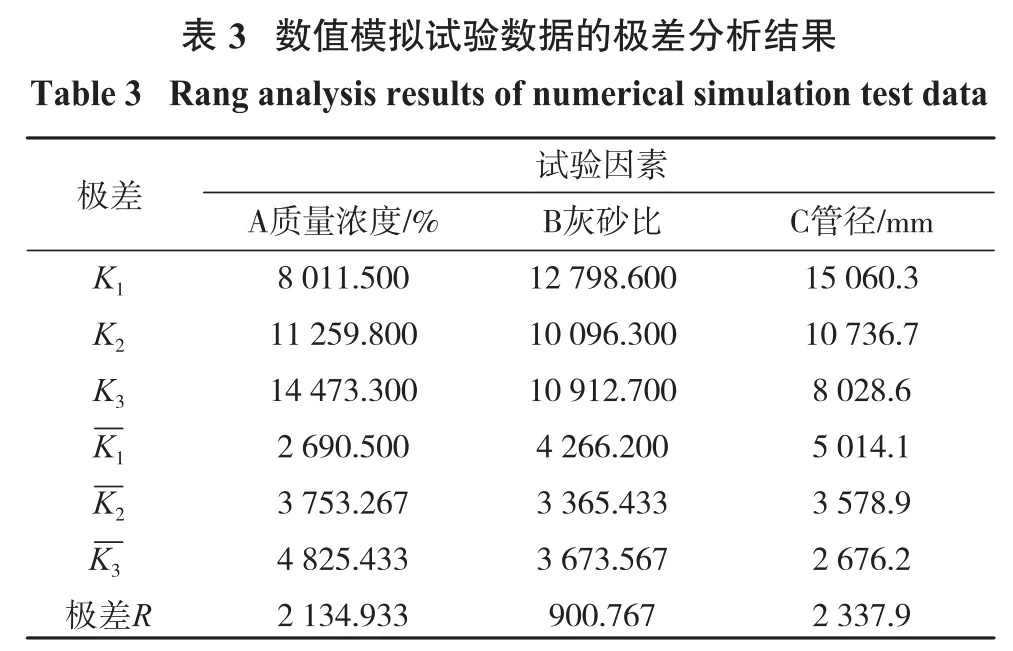
注：K1，K2，K3为每个因素各个水平下的极差总和为每个因素各个水平下的极差均值。

式中，Y为阻力损失，Pa/m；x1为质量浓度，%；x2为尾砂质量与水泥质量的比值；x3为充填管径，mm。回归方程的相关系数R=0.999 99，调整后Ra=0.999 97，可见回归方程较为显著，方程可靠程度高。

4 充填料浆管道输送阻力损失变化特征

4.1 管径对输送阻力的影响

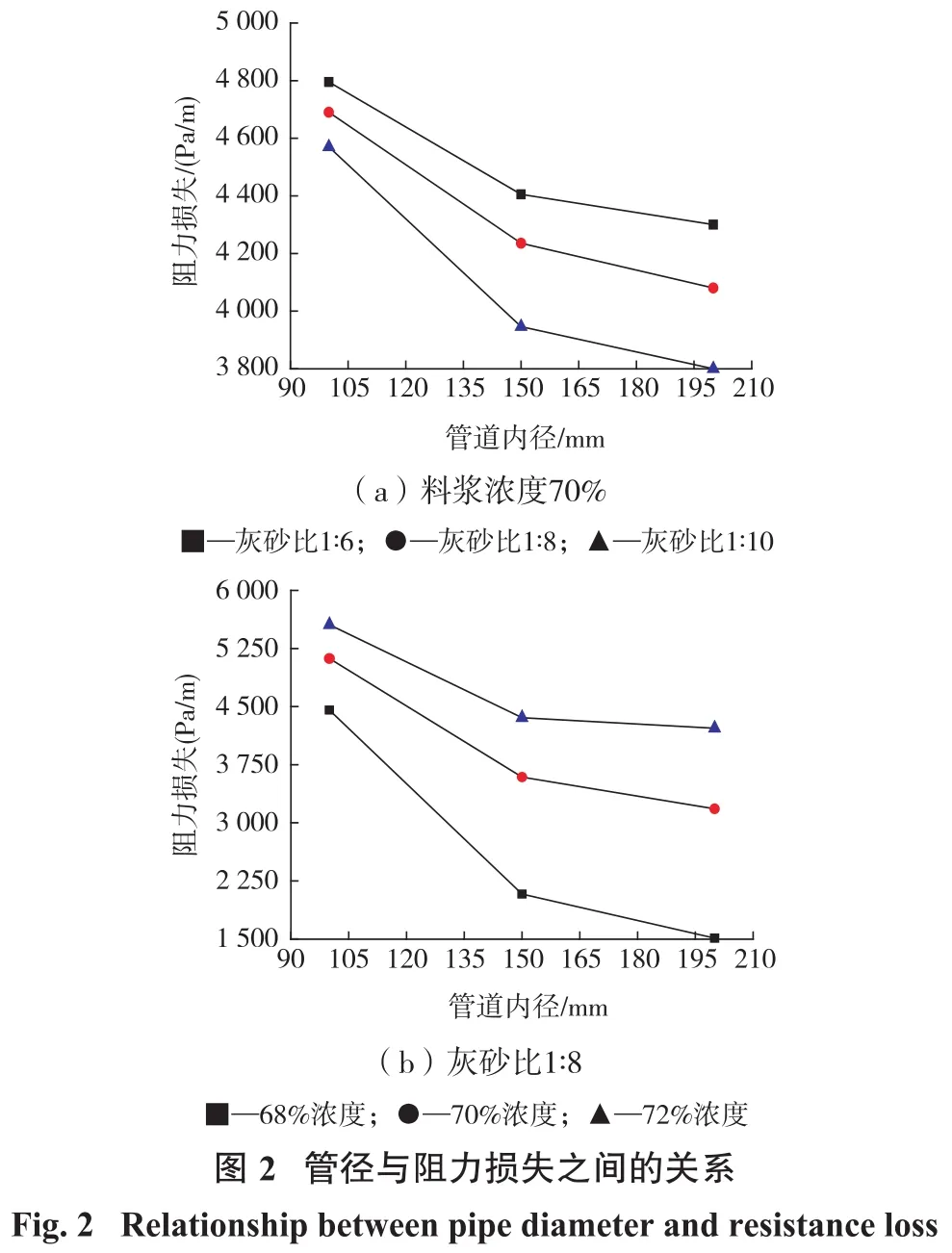
管径与管道阻力损失之间的关系如图2所示，可以看出管径与阻力损失呈负相关。图2（a）表明管径增大时，灰砂比对阻力损失影响的显著程度减小，3条曲线逐渐发散；图2（b）表明，灰砂比不变，浓度增大时，料浆流动的“黏性”增大，输送阻力越大。

高浓度料浆中尾砂颗粒迁移主要受到壁面剪切作用力影响，管径增大，壁面剪切作用力减小，颗粒的迁移运动变缓，滑移效应减弱，对摩擦阻力的抵消作用减小。管径较小时，滑移层的减阻效果明显，可以看出，管径为100～150 mm时，管道输送阻力快速降低；当管径增大到一定值时，料浆中的尾砂颗粒所受到的剪切作用力较弱，致其无法进行迁移运动，不能形成覆盖管道内壁的滑移层，此时滑移作用效果较弱，随着管径增大，管道输送阻力缓慢减小。

4.2 浓度对输送阻力的影响

料浆浓度与管道阻力损失之间的关系曲线如图3所示。由图3可知：料浆浓度与管道阻力损失基本呈正相关。图3（a）表明，管径不变料浆浓度增加时，管道输送阻力逐渐增大，同时可以看出灰砂比对输送阻力影响较大，水泥含量越高，阻力损失值越大。图3（b）反映灰砂比一定时浓度对阻力损失的影响规律，管径越大，管道阻力损失越小，同时随着浓度增大，图中3条曲线开始聚拢，说明浓度变化导致输送阻力的差异越来越小。

浓度较低时，料浆管道输送过程中滑移层的形成主因为静态壁面损耗效应［19］，滑移层主要由水构成。较小的剪切力作用下就会引发滑移流动，产生滑移效应，对管道形成“润滑”作用，其与料浆输送过程所受到的部分摩擦阻力相互抵消，随着浓度增大，输送阻力增长速率加快；浓度较大时，滑移层由尾砂颗粒的迁移运动控制，尾砂颗粒需要在较大的剪切应力作用下才会发生迁移运动，且浓度增大时，料浆流动性变差，摩擦阻力增大，二者相互作用下，管道阻力损失快速增长。结合图3（b）分析发现，料浆浓度超过70%时阻力损失增长过快，因此本研究推荐最大输送浓度不应超过70%。

4.3 灰砂比对输送管道阻力的影响

砂灰比与管道阻力损失之间的关系如图4所示，可以看出砂灰比与管道阻力损失呈负相关。图4（a）表明，管径一定时，管道阻力损失随着砂灰比增大而呈线性减小；图4（b）表明料浆浓度一定时，料浆中的水泥含量降低，管道阻力损失快速下降，当水泥含量低于一定值后，管道阻力损失减小的速率快速减小。

水泥遇水发生水化反应的过程会大量消耗料浆中的自由水，使得高浓度料浆浓度增大，表观黏度及屈服应力增加，导致料浆的流动性变差，料浆的黏性耗散量增大。同时由于滑移层的组成成分主要为自由水，当大量的自由水被消耗时，不能形成可以填充整个管道粗糙内壁的滑移层，此时管道输送阻力较大。当水泥含量下降（砂灰比增大）时，水化反应需水量下降，料浆流动性较好，可以形成有效的滑移层，此时管道输送阻力快速下降；当水泥含量较少时，其水化反应消耗的水对滑移层结构的影响较小，管道输送阻力降低速率减小。由图4（b）可知：料浆在管道输送过程中，灰砂比与阻力损失的关系曲线存在明显转折，当灰砂比超过1∶8时，阻力损失的降低速率明显变小，曲线趋于水平，灰砂比低于1∶10时会影响充填体强度的形成，因此本研究推荐的最佳灰砂比范围为1∶8～1∶10。

5 工程实例验证

冀东地区某矿为地下矿山，由于生产需要建有1座地面充填站，标高+110 m。该矿山采用全尾砂胶结充填技术进行充填作业。充填选用的尾砂来自选厂浓缩池，经浓缩后在搅拌桶中与水泥混合制备成浓度为70%～73%、灰砂比为1∶4～1∶6的充填料浆。充填料浆经砂浆泵加压后通过充填钻孔（钻孔长度110 m）进入地下采场。其中，充填管路内径180 mm，砂浆流量为100～140 m3/h，其中充填系统水平距离为2 100 m，竖直距离为500 m，坡面夹角为30°。该矿山充填系统如图5所示。为准确计算该矿山充填系统的输送阻力，以充填钻孔底端为0 m标高，根据矿山实际充填管路，建立了模型尺寸和充填管路尺寸比为1∶1的几何模型。

根据矿山充填料浆实际配比参数选择灰砂比为1∶6，浓度分别为72%、73%的料浆进行模拟试验。同时根据前述分析所得的参数最优取值范围，选择灰砂比为1∶8，浓度为66%、68%、70%的料浆进行对比验证，不同料浆所对应的流变参数如表4所示。

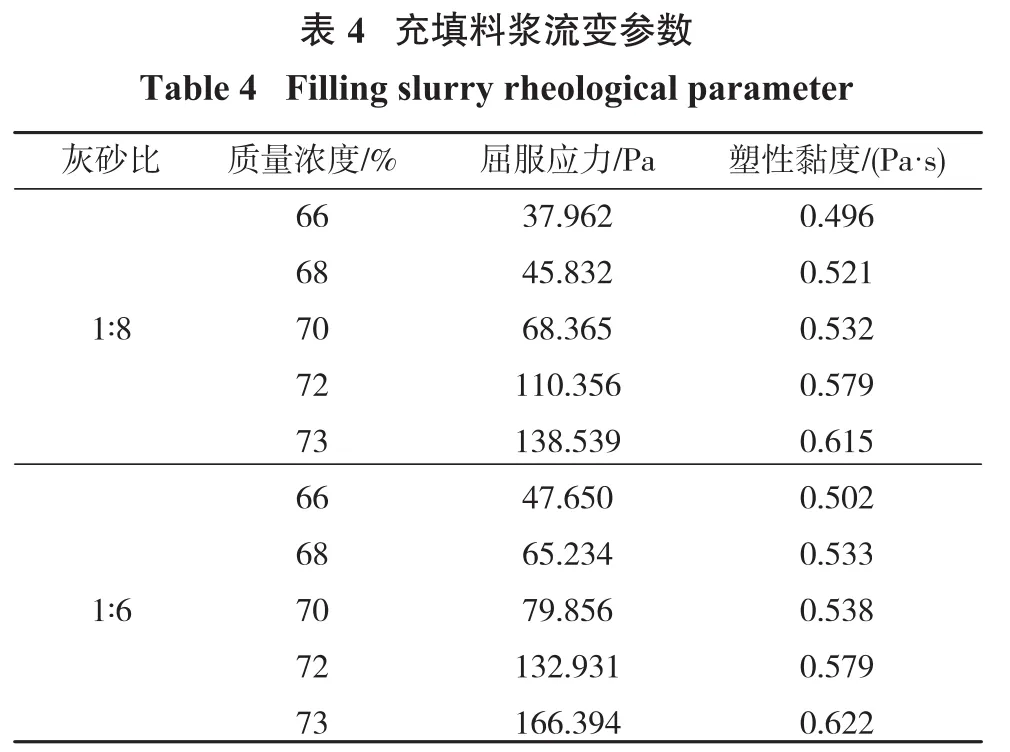
选择浆体初始速度为1.5 m/s进行模拟试验，结果如图6所示。由图6可知：当采用矿山实际充填参数时，管道输送阻力较大。矿山充填管道的输送阻力随着料浆浓度增加而快速增大，当料浆浓度小于70%时，可大大减小料浆管道输送过程中的能量损耗，同时也会降低堵管、爆管的风险。考虑到矿山充填结构体的强度需求，为有效提高矿山生产效率和减小渗水量，充填料浆浓度不宜低于66%，因此，得到本试验条件下料浆的最佳输送浓度为66%和68%。灰砂比由1∶6降低为1∶8时充填管道的输送阻力减小，但是水泥含量过低时会影响矿山充填体早期强度形成。当灰砂比大于1∶10时，水泥含量变化对充填体强度的影响较小，同时基于管道输送阻力的变化情况得出该试验条件下的最佳灰砂比为1∶8。