CA-3F车钩钩体强度校核及可靠性分析
2020-10-26吴昊臻陈天星李天成
吴昊臻,陈天星,李天成,杨 创
(西南交通大学机械工程学院,成都 610036)
0 引言
CA-3 型车钩是一款老型自动车钩,20 世纪30 年代年起就被确定为标准车钩。其具有刚性好、连挂操作简单等优点。使用至今其还衍生出Willison 车钩、CA-4 型车钩、LAF车钩等。CA-3 自动车钩如图1 所示,主要应用于亚美尼亚、阿塞拜疆、俄罗斯、白俄罗斯、立陶宛等欧洲国家和哈萨克斯坦、吉尔吉斯斯坦、伊拉克等西亚国家以及澳大利亚。

图1 CA-3车钩

图2 CA-3F车钩模型
CA-3型车钩主要缺点有:在两钩头连挂处缺少限置车钩上下偏移的装置,在使用过程中两连挂车钩在竖直方向上会出现偏移;钩尾销孔处易产生很高的接触应力,垂直竖扁销的联接方式,使得车辆的弯道通过性不好,且在使用过程中易在钩尾销处产生很高的接触应力;钩尾端面采用的是圆柱面结构设计,在车钩运行使用中,车钩的自动对中性不强等[1]。
本文参考借鉴17 号车钩和法国的LAF 型车钩,在保留CA-3车钩钩头的主要结构不变的情况下,钩尾借鉴17号车钩钩尾结构,钩头借鉴LAF 车钩的锁扣结构,设计出CA-3F 型自动车钩。图2所示为CA-3F车钩设计模型。
利用ANSYS中对CA-3F车钩钩体进行静强度分析,并根据分析结果与车钩实际使用中出现的疲劳破坏情况,合理选择疲劳控制点对CA-3F车钩钩体进行疲劳校核,利用ANSYS APDL中的PDS模块编写程序对钩体进行可靠性分析,能有效的保证钩体的强度,减少了产品的研发周期与成本。
1 钩体静强度分析
1.1 钩体材料与网格划分
CA-3F车钩各零部件均采用铸造生产,钩体铸造材料为E级铸钢。表1、2 分别为铸造E 级钢ZG25MnCrNiMo 主要性能指标和材料属性。

表1 铸造E级钢ZG25MnCrNiMo主要性能指标

表2 铸造E级钢ZG25MnCrNiMo的材料属性
利用Inventor软件建立CA-3F车钩钩体的三维模型,对非承载的结构进行简化并将模型导入ANSYS 中。图3 所示为得到的有限元网格。

图3 CA-F车钩钩体网格
1.2 静强度加载及评定标准
CA-3F 车评定标准参考TB456-2008 中17 号车钩评定标准,在TB456-2008中规定了国产车钩的静强度实验标准。其中规定E 级钢车钩在3 115 kN 纵向拉伸载荷作用下,钩体静置一段时间后,最大变形量不超过0.8 mm,钩体在4 005 kN纵向拉伸载荷作用下,钩体不得发生破坏。表3 所示为E级钢CA-3F车钩钩体标准载荷工况。

表3 CA-3F车钩钩体标准载荷工况
实际运营载荷是钩体疲劳分析的基础载荷,是指在运行中钩体出现的次数最为频繁的最大载荷。Colin Cole等研究在复杂列车系统下的稳定数据,数据显示较高频次的最大拉伸载荷统计值在1 000 kN左右[2]。取1 000 kN作为车钩实际运营载荷,CA-3F车钩在空载作用下的载荷参考国产17号车钩的空载时的载荷。表4所示为E级钢CA-3F车钩钩体实际载荷工况。

表4 CA-3F车钩实际工况
生产CA-3F 车钩钩体材料为E 级钢,属塑性材料,在进行强度评定时应采用第四强度理论,按照Von-Mise应力屈服准则。等效应力由第四强度理论推导而得:
式中:σe为等效应力,MPa;σi(i=1,2,3)为应力,MPa。
钩体强度校核结果需满足条件:

式中:[σ]为许用应力。
有限元分析的约束设置如下。(1)拉伸工况:车辆行驶时,车钩传递牵引力,处于拉伸状态,此时在小钩腕的右侧面和大钩腕的右侧面施加固定约束,在钩身零件钩尾销孔处右侧的圆弧面施加水平向右的载荷。(2)压缩工况:车辆制动时,车钩传递制动力,处于压缩状态,此时在小钩腕左侧面和大钩腕右侧面施加固定约束,在钩身零件钩尾销孔处左侧的圆弧面施加方向水平向左的载荷。
1.3 钩体静强度分析结果
图4 所示为钩体在标准载荷工况一下的钩体变形分布云图,CA3-F 车钩钩体在3 115 kN 载荷下最大永久变形量为0.64 mm,小于0.8 mm,符合TB 中的使用要求,处于安全状态。图5所示为钩体在标准载荷工况二下的钩体等效应力分布云图,CA3-F车钩钩体在4 005 kN载荷作用下的最大等效应力为638 MPa,小于830 MPa,符合TB中的使用要求,处于安全状态。

图4 CA-3F车钩钩体永久变形分布云图

图5 最小破坏载荷应力分布云图
CA-3F 车钩钩体在实际载荷工况中,重载拉伸工况中钩体最大等效应力为234 MPa,在钩体的小钩腕处,如图6 所示。在重载压缩况中钩体受到的最大等效应力为227 MPa,在钩体的钩肩处,如图7所示。

图6 重载拉伸工况应力分布云图

图7 重载压缩工况应力分布云图
车钩在空载拉伸工况中受到的最大等效应力为73.7 MPa,在钩体的小钩腕处,如图8所示。重载拉压缩况中受到的最大等效应力为105 MPa,在钩体的钩肩处,如图9 所示。4 种实际运营工况下,钩体最大等效应力均小于E 级钢的屈服极限690 MPa。

图8 空载拉伸工况应力分布云图

图9 空载缩况工况应力分布云图
2 钩体静强度校核
2.1 修正的Goodman-Smith疲劳极限图
根据《暂行规定》,我国机车车辆在校核车辆零部件强度时,选取修正Goodman-Smith疲劳极限图来评定疲劳强度[3]。
机械零部件的疲劳极限与材料的疲劳极限有关,影响机械零部件的疲劳极限的因素有形状因素、尺寸因素和表面加工精度等。CA-3F 车钩钩体的疲劳极限可以由材料的疲劳极限得到公式:

式中:σ-1N为机械零部件的疲劳极限;β-1为表面加工系数;ε为尺寸系数;k为应力集中系数;σ-1为材料的疲劳极限。E级钢的屈服极限σs=690 MPa,强度极限σb=830 MPa,查阅相关文献,参考国产E 级钢17 号车钩,取223 MPa 作为CA-3F车钩钩体疲劳极限[4]。
CA-3F车钩钩体的疲劳极限图如图10所示。

图10 修正的钩体疲劳极限图

图11 钩体强度疲劳校核图
2.2 疲劳控制点的选取
CA-3F 车钩钩体的疲劳校核控制点的选取:根据实际运营工况下的应力值较大的部位,再结合CA-3型车钩在使用中钩头常见的裂纹发生部位以及17号车钩在使用中钩尾常见裂纹发生部位选择合适的控制点。疲劳控制点位置如下:位置1为钩尾销孔内部,位置2为钩尾与钩头连接处,位置3为小钩腕根部处,位置4为大钩腕外弯处,位置5为大钩腕外弯处。
利用疲劳极限图校核强度首先需要得到在实际运营工况下各控制点的最大、最小应力值σmax和σmin,并根据公式(4)、(5)计算出各控制点平均应力值σm和应力幅值σa。

利用ANSYA提取各控制点处最大、最小应力值,并计算得到各点的坐标,表5所示为各控制点坐标。
2.3 疲劳强度校核
疲劳强度校核评价标准:疲劳校核点处于疲劳极限图内部时,认为材料或者结构安全,疲劳强度符合要求。利用修正的钩体疲劳极限图对所选的5个控制点进行校核。其结果如图11 所示,5 个点均在曲线内,说明CA-3F 车钩钩体的疲劳强度符合要求。

表5 控制点坐标
3 钩体可靠性分析
3.1 可靠性方法
可靠性是衡量产品质量的一个重要指标,是用来描述产品在规定工况和使用周期内能够正常工作的能力[5]。在对结构进行可靠性设计时,将相关参数都看作随机变量,如载荷、强度、尺寸、寿命等,这些变量的数据可以采取试验方式进行收集,然后运用数理统计理论对收集数据进行处理,得到相关参数的分布规律,建立合理的数学模型依据应力-强度干涉等理论进行可靠性分析,可得到结构或系统的可靠度估计值。
在可靠性理论中常用的概率分布分为两种:连续型随机变量分布和离散型随机变量分布。
应力-强度分布干涉理论中的随机变量应力、强度均属于连续随机变量分布中正态分布。其密度函数服从正态分布:

其分布函数为:
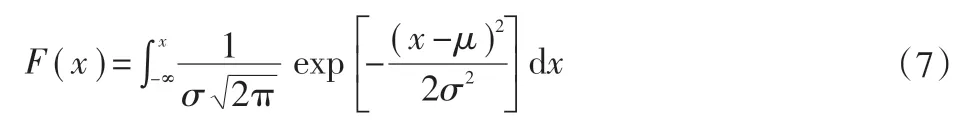
式中: -∞<x<+∞ ;σ为标准差,σ>0 ;μ为集中趋势(可为均值、中位数或众数),-∞<μ<+∞。
3.2 Monte Carlo方法
常用的可靠性分析方法可分为3 种类型:近似解析法、数学模拟法以及响应面法(函数代替法)。采用数学模拟法中Monte Carlo 法可以很好地求解涉及到多维积分或者积分域较复杂的可靠性分析问题[6]。
蒙特卡洛方法在可靠性问题中求解失效概率Pf的一般过程是:首先依据联合概率密度函数fx(x) 产生随机变量的N个随机样本xj(j=1,2,3,…,n) ,然后将产生的N 个样本代入g(x1,x2,x3,…,x4) 功能函数中, 并对落入失效域F={x∶g(x)≤0}的样本进行统计记为Nf,得到失效频率Nf/N,用其近似失效概率Pf,这样就可以得到母体失效概率的估计值。

式中:IF(x)为失效域指示函数。
结构或者系统的可靠度估计值如下:

采用ANSYS 概率设计模块(Probabilistic Design System,PDS)对CA-3F 车钩钩体进行可靠性分析,定义钩体的输入变量以及输出变量,利用ANSYS提供的蒙特卡洛方法,可以得到车钩钩体的静强度可靠度。
3.3 输入输出变量
定义可能会影响分析结果的随机输入参数和关心的随机输出参数,选择合适的可靠性分析方法和抽样方法是蒙特卡洛方法的关键。
3.3.1 载荷输入变量
在实际运行中,钩体的实际工况载荷较标准工况载荷,对钩体强度和寿命影响最大的是实际工况载荷。且在实际工况中,重载拉伸工况中钩体的最大应力最大,因此选用该工况来对钩体做可靠性分析。将该工况下的载荷作为可靠性分析的输入载荷。
查阅相关文献可知钩体载荷服从正态分布,其概率密度函数如下所示:

式中:μ、σ分别为正态分布的均值和标准差。
输入载荷的正态分布均值取重载拉伸工况的载荷值,由下式可求得输入载荷的标准差:

式中:C为变异系数,由于车钩模型较复杂,在进行可靠性分析时很难参数化车钩的模型,因此取C=0.05 作为载荷变异系数[7]。
3.3.2 E级钢输入参数
在工程实际中,材料的弹性模量、许用应力、泊松比通常都近似服从于正态分布[8]。查阅相关文献知E级钢的许用应力为345 MPa,将材料参数弹性模量、泊松比、许用应力作为可靠性分析的随机输入变量并作为正态分布的均值,其标准差可通过公式(11)得到。查阅相关文献,取0.015、0.02、0.05 作为各输入变量的变异系数[9]。表6 所示为可靠性分析的随机输入变量。

表6 可靠性分析输入变量
3.3.3 随机输出变量的确定
将钩体在重载拉伸工况下的最大等效应力MAXVON设置为可靠性分析的输出变量。
3.4 钩体可靠性分析结果
在可靠性计算中,蒙特卡洛方法模拟的次数直接影响结果的精度,因此将模拟实验的次数取为5 000次。图12所示为输入载荷的抽样样本。

图12 输入载荷抽样样本
钩体的最大等效应力MAXVON 作为可靠性分析输出变量。图13 所示为MAXVON 样本历史曲线。从MAXVON 的样本历史曲线可知MAXVON 的值是收敛的,在3 750 次后曲线趋近于直线,说明可靠性分析结果收敛良好。

图13 最大等效应力样本历史曲线
图14所示为可靠度结果,通过查看结果,钩体的最大应力小于许用应力345 MPa的概率为1,即钩体的静强度可靠度为1,其置信度为0.95。
4 结束语
本文利用ANSY 基于国家标准和Colin Cole 等人提出的重载货车实际运营载荷理论,对CA-3F 车钩钩体进行了有限元分析,并结合CA-3 型车钩和17 号车钩在使用中常出现的疲劳破坏部位,选用修正的Goodman-Smith 疲劳极限图对钩体进行疲劳校核,并依据可靠性理论和蒙特卡洛方法,在ANSYS PDS 模块中编写程序计算得到CA-3F 车钩的钩体可靠度。计算与分析结果表明钩体的最大永久变形为0.64 mm、最小破坏载荷大于或等于4 005 kN,均符合TB456-2008 中规定的标准,钩体的疲劳强度亦符合使用要求,CA-3F 车钩钩体可靠性分析结果表明钩体的可靠度为1,其结果致信度为95%。在车钩投入生产前,本文系统全面地对CA-3F 车钩的钩体进行了分析计算,可用于同类型产品在投产前进行分析,减少产品的研发周期和研发成本。

图14 可靠度结果
