融合泛在网络与物联网技术的职业院校智慧校园建设研究

郑 琦

（福建商贸学校，福建 福州350007）

一、引言

泛在网络（UN）是指一种自组织类型的网络，其中包括空间分布的自主传感器设备。这些传感器设备通过网络相互连接，并监视目标区域的环境。信息和通信技术（ICT）的最新发展已导致小型化和复杂的传感器设备（例如，低功率广域网，而UN 是进一步高级网络系统的基础，它们在实现物联网和网络物理系统时引起了极大的关注。在这些情况下，将在Internet上集成和实施许多ICT应用服务和其他社会基础设施。但是，泛在网络与物联网技术没有考虑模块间链接的端点；因此，这项研究考虑了分类性，即被定义为网络中节点度的相关性。节点度是最简单、最常见的集中度度量之一，用于度量网络拓扑上的节点重要性。在具有高分类性的网络中，如果两个节点具有相似的节点度，则可能会互连一对节点。相比之下，在具有低分类性的网络中，如果两个节点的节点度不同，则将它们连接起来。至于由多个模块组成的泛在网络，分类可以表示不同的行为，这取决于焦点是模块之间还是模块内部的连接，以及模块之间的连接是强还是弱。脑网络的高可靠性可以归因于拓扑连通性，它是基于网络模块之间和内部的分类性。

这项研究的目的是为职业院校智慧校园设计一种模块化的网络拓扑结构，这种拓扑结构可以抵抗环境变化，并以相对较低的布线成本提供较高的通信效率。对于智慧校园网络的构建，首先根据提出的方法分配模块之间的链接；其次，通过考虑分类性，提出了一种在模块内的节点上分配模块间链接的方法。泛在网络与物联网技术和分类性的影响可以通过单个参数来控制。

二、泛在网络与物联网技术

泛在网络可以看作是一个复杂的网络，包括位于髓鞘绝缘轴突连接的皮质灰质区的神经元细胞体。神经影像技术的最新进展使得能够以更高的空间分辨率对泛在网络进行分析。先前的研究已经检查了以感兴趣区域之间的解剖联系为代表的大脑结构网络。在此过程中，选择了空间分布的91个皮质区域中的29 个，以便29 个区域的子图可以完全估计整个网络的连通性。逆向示踪剂注入到这29 个区域中，表明存在6,494,974 个神经链接和1615个区域间链接。分析表明，区域间连接的存在概率p（d）随区域间距离呈指数衰减，可以表示为：

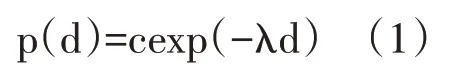
其中c 表示归一化常数，d 是区域间距离，而λ是参数。为了近似大脑的连通性，在泛在网络与物联网技术中使用了λ=0.180mm-1。应当注意，在结果拓扑中的链接被分配了与区域之间的多个神经连接相对应的权重。考虑到代谢成本和性能之间的折衷，紧邻的神经元往往具有更多的连接；此外，还提供了一些长距离连接来加速信息集成。即使泛在网络与物联网技术是仅由单个参数λ控制的相对简单的模型，它仍可以充分再现泛在网络中拓扑连接的各种属性，例如通信效率、派系分布、特征向量谱及存在核心结构。

基于剩余度分布q（k）计算全局分类系数，如下所示：

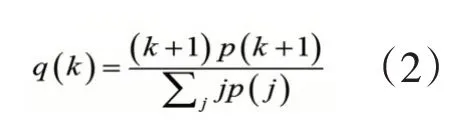
其中称为度数分布，它表示随机选择的节点具有节点度数k的概率；称为剩余度分布，它表示随机选择的链接的任一端点节点具有剩余度k 的概率。在此，节点的剩余度是指普通节点度减去节点本身。全局分类系数r定义如下：

其中J 和K 表示剩余程度的变量；两者具有相同的期望值。项表示剩余度分布的方差。r的正值和负值分别表示网络是分类的和分解的。当r趋于零时，网络变为非分类网络；网络的形状变得类似于随机网络的形状。从理论上讲，r 的可行值范围是[-1，1]；但是，由于度分布，其范围变小。

然后，在给定的情况下，可以引入链路l上的通用分类系数。该系数对应于单个链接对全局分类系数r的贡献。因此，定义如下：

其中j和k表示链接l的两个端点的剩余度。此处，M表示网络中的链路总数。

三、构造职业院校智慧校园网络方法

物理层上的模块通过网关（边缘服务器）之间的模块间链接的无线连接泛在地彼此连接，并形成泛在层。关于模块间链路的端点的分配，在实际意义上，物理层上的所有节点都不能充当端点，因为设备的性能或角色彼此不同。但是，在此评估中，假设所有节点都有能力充当端点节点。因此，的目标是从拓扑的角度揭示应表示为端点节点的节点类型。如图1所示。

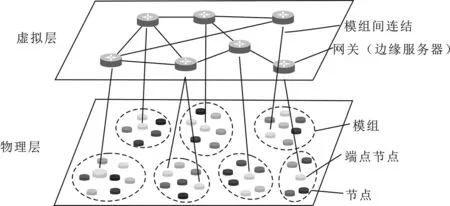
图1泛在化泛在网络的架构

在以下小节中，将描述为职业院校智慧校园网络体系结构构建泛在层拓扑的建议方法。首先，泛在网络与物联网技术被修改并用于职业院校智慧校园间链路的部署。然后，应用分类性来确定模块中节点上模块间链接的端点的分配。

为了创建模块间链接，将等式（1）重新定义为等式（6），以使泛在网络与物联网技术中的变量和参数可以适应除皮质区域间连通性以外的任何规模的网络拓扑：

其中dn表示两个模块之间的相对距离。也就是说，dn=d/dmax，其中实际欧几里德距离dmax除以所有模块对中的最大距离。

本文从节点分类的角度讨论将模块间链接的端点分配给节点的过程。即，选择端点节点，以使得在每对模块的模块间连接性上获得等式（5）中的分类性ρ 的指定值。通过使用这种分配方案，排除了已经存在模块间链接的端点对。为了获得合适的模块间连接性，以实现指定的分类值，模块间链路进行了重新布线。图2显示了根据上述过程生成的两个示例网络，其中每个链路都是未加权和未定向的。

图2 职业院校智慧校园网络互连性

四、仿真结果与分析

本文介绍了除泛在网络与物联网技术以外的用于在模块内部和模块之间分配链接的网络模型。此外，还定义了评估通信效率，智慧校园网络稳定性性和网络建设成本的指标。还将解释用于为计算机仿真构建职业院校智慧校园网络的特定参数设置。

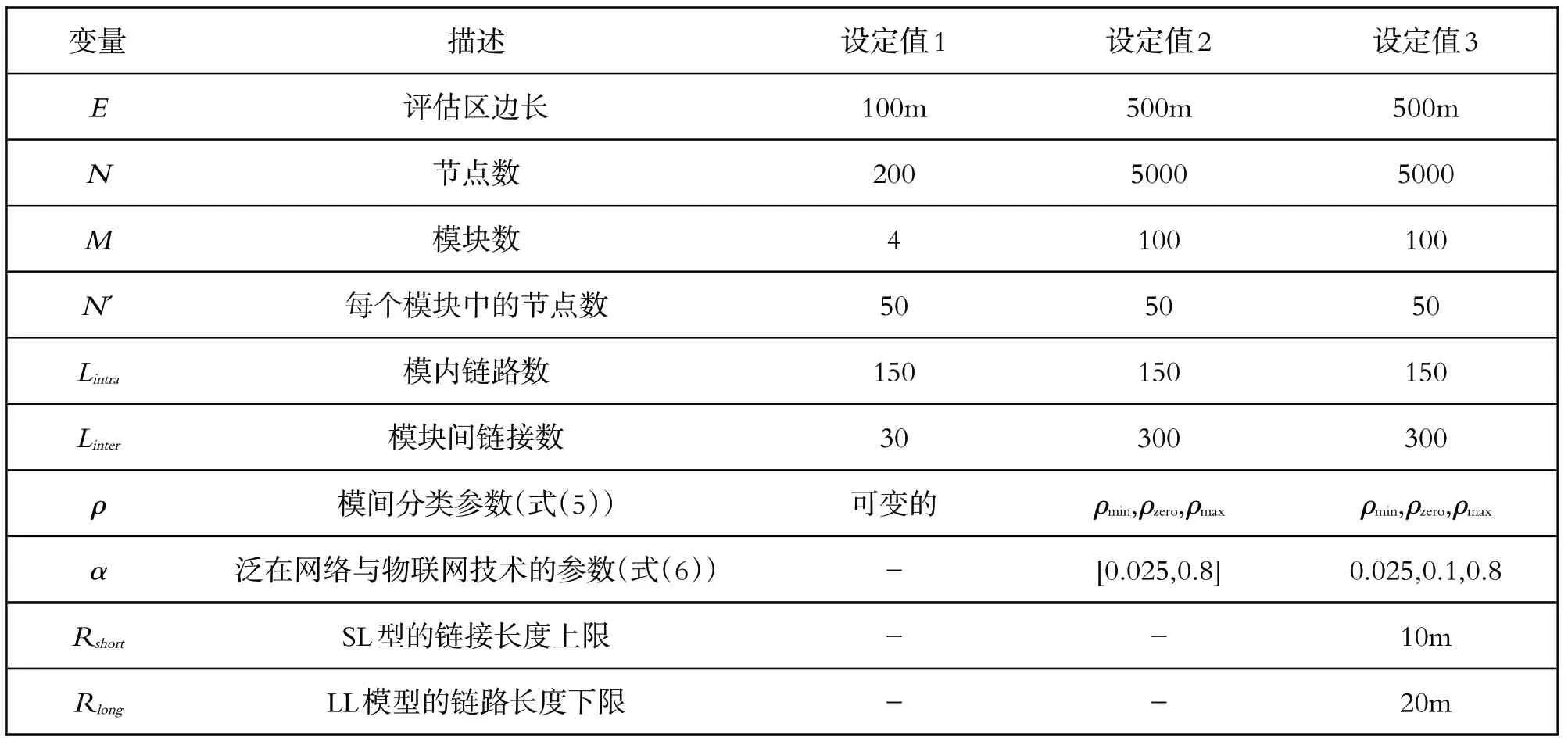
在计算机仿真中，假设职业院校智慧校园网络构造在E×Em2的正方形区域上，并且将N 个节点部署为物理节点。该区域以网格图案划分为M 个较小的区域，每个区域包含相等数量的N'=N/M 个节点。分别基于SL 模型和LL 模型构造职业院校智慧校园网络时，Rshort和Rlong限制了链接的长度。

?

参数设置如表1所示。职业院校智慧校园网络由M=4 个模块组成，如图3 所示。每对模块均被平均分配5 个模块间链接，而职业院校智慧校园网络的Linter=5×6=假设有4C2=6 种可能的组合，则有30 个模块间链接用于连接四个模块中的两个。当比较ER 模型和BA 模型的结果时，对于任何给定的分类价值，后者显示出更强大的功能。这可以归因于节点度分布的差异。在基于BA 模型的拓扑中，集线器节点的密集中心核心紧密连接所有节点并增强了连通性。这样可以减小直径并缩小网络的拓扑形状。因此，一些故障不会分裂BA 模型的拓扑。相反，基于ER 模型的拓扑连接稀疏且统一，并且可以轻松拆分为较小的群集。这些特征导致ER 模型和BA 模型之间的代数连通性不同。

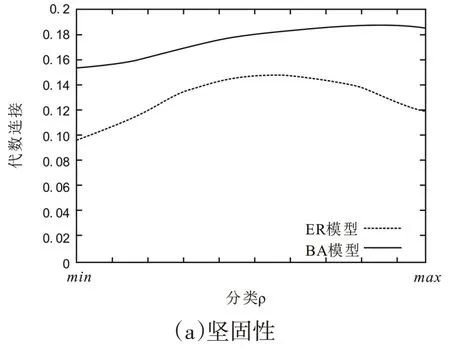
图3 模块网络的仿真结果

如表1所示，因为职业院校智慧校园网络已在正方形区域中移至更大的比例，所以N'和Lintra 使用相等的值。确定模块间链接Linter 的数量为Linter=3×M=300，以便每个模块添加三个模块间链接。因为在前面的文章中已经研究了分类能力ρ对性能的详细影响，

图4 显示了代数连通性，泛在网络与物联网技术中的参数α和模间分类之间的关系。y轴表示代数连通性，而x轴表示参数α。这两个子图包含三个曲线，每个曲线分别对应于模块之间的分类，分类和非分类连通性。关于分类性，应该注意的是，在ER模型和BA模型中，分类拓扑都展现出最高的代数连通性，即最鲁棒的特征。但是，在4 模块网络的ER模型中，证实了非分类或略分类的连通性可实现最高的鲁棒性。这可能归因于模块数量的差异。在4模块网络中，每个模块通过一跳连接到所有其他模块。但是，在这种情况下，职业院校智慧校园网络由100 个模块组成，因此，大多数模块对是间接连接的。从该结果可以推测，当两个节点之间的路径经过多个模块时，由两个高级节点组成的模块间链路会导致不连续路径数量的增加。这导致代数连接性，即鲁棒性的增加。在BA模型中，高阶节点之间的连接影响较大，而分类拓扑可实现更高的鲁棒性。

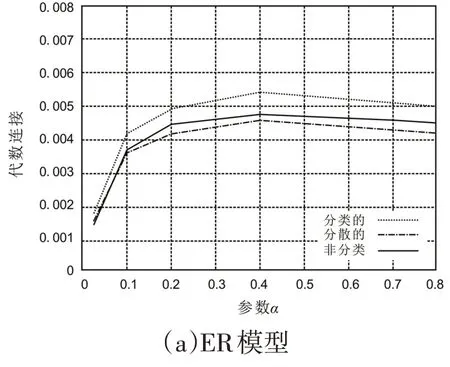
图4 智慧校园网络稳定性性

五、结论

本文提出并评估了一种构建职业院校智慧校园网络的方法。由于未来的职业院校智慧校园上存在大量的物联网技术设备和无数类型的应用程序服务，为了满足所需的性能。在现实世界的物联网网络中，供应商对环境或服务需求的各种限制可能会影响边缘计算系统和UN 上职业院校智慧校园网络的构建。可以总结为，相互连接的高级节点既增强了鲁棒性，又提高了通信效率。同时，提出的方法可以帮助设计职业院校智慧校园架构，以应对实际物联网场景中可能出现的各种需求。