基于Wiener 模型的非线性系统的鲁棒预测控制

封晓宇 张冬雯

（1、河北科技大学电气工程学院，河北 石家庄050018 2、河北科技大学信息科学与工程学院，河北 石家庄050018）

预测控制是从工业控制过程中兴起的一种新型计算机控制方法。因为预测控制的应用价值较高且应用范围的较为广阔，所以在控制领域预测控制成为热门研究的对象[1-4]。

在实际生产过程中，非线性系统普遍存在且研究较多的，正是由于该原因，所以针对非线性系统预测控制目前已有很多研究成果[5]。文献[6]针对一类非线性不确定系统，根据时滞和不确定性选择了相关的李雅普诺夫函数，通过线性矩阵不等式和变量变换对设定的二次函数性能指标的最小值进行了求解，得到闭环系统稳定性的充分条件。

Wiener 模型之所以能够在工业过程中得以广泛应用，是因为其能很好的描述一大类非线性对象。文献[7] 提出了基于Wiener 模型的改进式非线性预测控制算法。Laguerre 级数展开式描述Wiener 模型的线性部分，在Wiener 模型的非线性部分利用静态模糊模型进行描述，此时的非线性系统则可采用线性预测控制的方法求解预测控制律，避免了直接对非线性系统进行优化求解。

本文针对一类Wiener 模型描述的非线性时滞系统，研究了Wiener 模型的预测控制问题。采用Lyapunov-Krasovskii 函数设计了每个子系统的状态反馈控制律，在"min-max"的性能指标下，求解了优化问题，得到了系统渐近稳定且具有较小保守性的充分条件。

1 问题描述

考虑如下离散状态空间模型描述的非线性时滞系统：

其中，x（k）∈Rn为状态向量，u（k）∈Rm为输入向量，y（k）∈Rq为输出向量，d 为时滞常数。

通过Wiener 模型来近似描述非线性时滞离散系统（1）。其中Wiener 模型是由一个线性单元与一个非线性单元串联组成，动态线性单元由状态方程描述，静态非线性部分由T-S 模糊模型进行线性逼近。非线性时滞离散系统（1）可以被分割成j（j=1，…，L）个局部子系统，每一个子系统的模型用以下模糊模型表示：

在规则Rj下

IF z1（k）is Vj1，zg（k）is Vjg

THEN

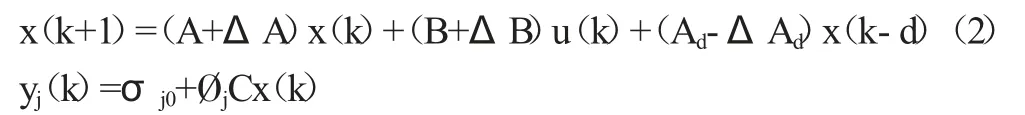
其中A，B，Ad，C 为具有适当维数的已知常数阵，Z（k）=[z1（k）…zg（k）]T为前件变量，j∈（1，…，L），L 为模糊规则数，Vjα（α=1，…，g）为模糊合集；Øj和σj0分别为在j 条规则下常数矩阵，ΔA，ΔB，ΔAd表示具有适当维数的不确定时变矩阵，假设不确定性时变矩阵是范数有界的，且具有以下形式：

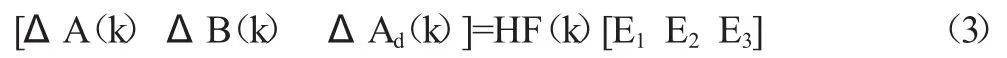
其中，H，Ea（a=1，2，3）表述具有适当维数的已知常数阵，F（k）是时变矩阵，表示模型的不确定性，且满足FTF（K）≤I，其中I 表述具有适当维数的单位矩阵。

通过采用平均加权反模糊化，非线性时滞离散系统（1）最终可以表示为：

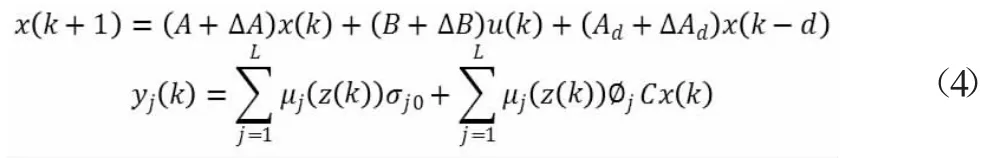
考虑无限时域的鲁棒预测控制，设滚动优化的性能指标为：

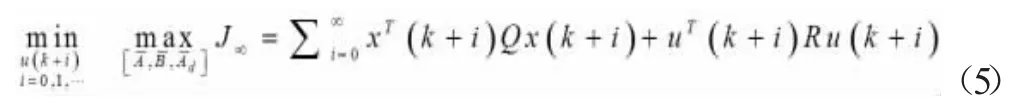
其中，Q＞0，R＞0 均为已知对称正定权矩阵。最优问题（5）是一个min-max 问题，表示所有可能的使得性能指标取最坏情况下所有可能的不确定矩阵以及使最小化最差性能指标时的输入问题。

第j 条规则下的控制律为u（k+i）=Kjx（k+i），其中Kj为第j条规则下相应的状态反馈增益。

非线性时滞离散系统（1）的控制目标是在每个采样周期内，通过求解优化问题（5），得到非线性时滞离散系统（1）的模糊控制律u（k+i）=Kμx（k+i）。

为能够得出结论，首先列出如下引理：

引理1：给定适当维数的矩阵G1，G2和对称矩阵Ω，对所有满足FT（t）F（t）≤I 的矩阵F（t），有

Ω+G1F（t）G2+G2TFT（t）G1T＜0

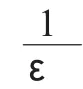
2 非线性预测控制器设计与算法

在每一采样周期，为了得到无限时域性能指标的上确界，采用了一个不等式条件，这时无限时域的优化问题，就转化为最小化上确界的最坏情况的求解问题，即“min-max”问题。然后通过利用线性矩阵不等式来给出状态反馈模糊控制器的表达式。

非线性时滞离散系统（1）是由L 个子系统加权反模糊所得，故当每个子系统都能使优化问题（5）有解，那么整个非线性时滞离散系统的优化问题必然有解。

针对非线性时滞离散系统（1），在每个子系统均采用如下Lyapunov-Krasovskii 函数：

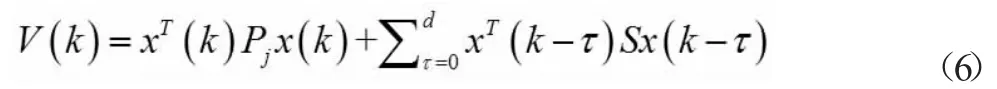
其中Pj＞0，S＞0。

为保证非线性时滞系统的鲁棒稳定性，在每个子系统的采样周期内对于所有可能的不确定时变矩阵和控制律，要求Lyapunov-Krasovskii 函数满足下列约束：

要使无限时域性能指标有界，则应满足收敛性，对式（7）从i=0 到i=∞进行求和，此时可以得到无限时域性能指标的上界，且无限时域性能指标的最坏情况转化为

故“min-max”问题则转化为求解式（8）最小化的解。

定理：考虑时滞非线性离散系统（1），假设x（k）为采样时间k 的测量状态，若各子系统存在正定矩阵Tj＞0，Yj，W 以及标量γ＞0，ε＞0，使得如下线性矩阵不等式有可行解：

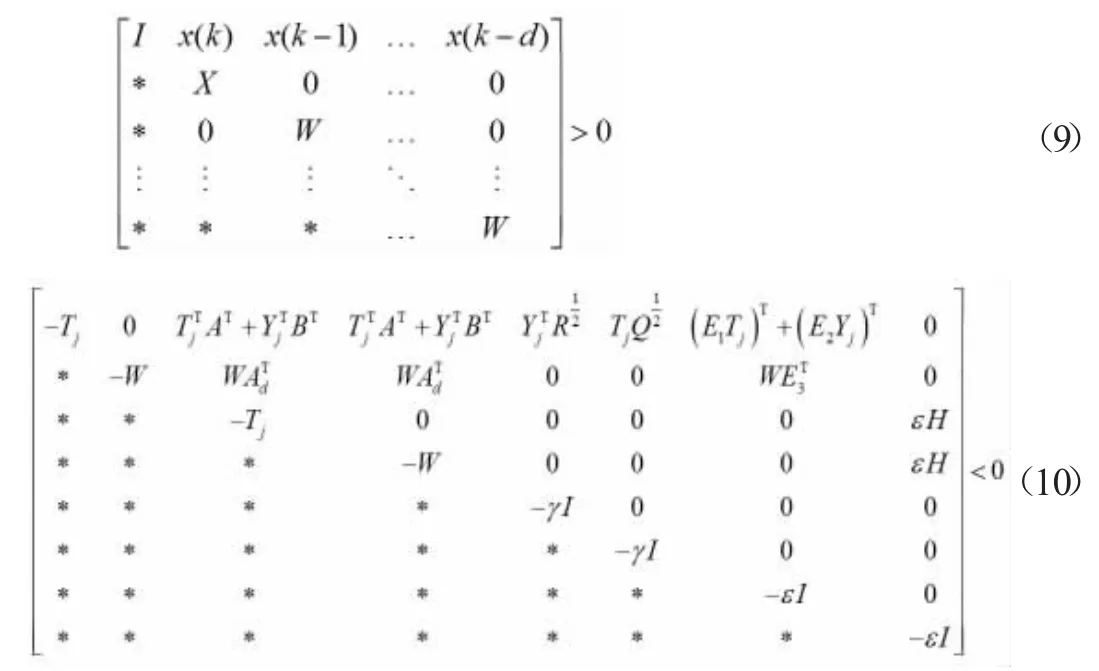
则对于由式（2）和各子系统的控制律组成的子闭环系统渐近稳定，并最小化性能指标的最坏上界。且子系统的控制器的增益为Kj=YjTj-1（j=1，…，L）。

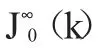
令Tj=γPj-1，W=γS-1带入式（6），并利用Schur 补引理可得式（9）。

3 仿真实例

为证明上述方案的可行性，采用由Wiener 模型描述的连续搅拌釜式反应器的放热反应过程进行仿真验证。反应器体积为V=100l，进料流量为F=100l/min，反应温度为T=438.54，活化能E/R=1×104，进料浓度CAf=1mol，反应率常数K0=7.2×1010，热传递系数hA=7×105cal/（min·K），冷入口温度Tc=350K，进料温度Tf=350K，密度ρ=1×103g/l。通过辨识，采用MATLAB 软件进行仿真，仿真结果如图1 所示，可以看出该算法能够使得输出稳定至稳定点。

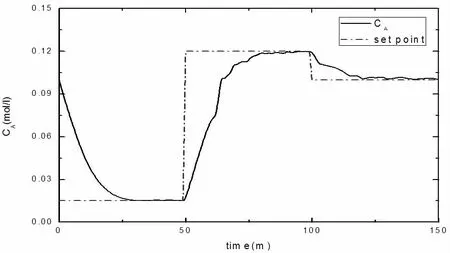
图1 反应物浓度曲线

4 结论

本文以一类Wiener 模型描述的非线性系统为研究对象，结合预测控制原理与模糊理论，研究了基于线性矩阵不等式的预测控制器算法设计问题，利用Lyapunov 函数设计了状态反馈控制律，推导出了闭环系统渐近稳定和性能指标最优化的充分条件，减少计算量，得到较小保守性。