电感交叉耦合对高频注入法的影响及补偿方法
2020-10-26王心坚马瑞盛黄道锦
王心坚,马瑞盛,黄道锦
(同济大学 汽车学院,上海 201804)
0 引 言
永磁同步电机由于其功率密度大、效率高等优点,近年来得到了广泛的应用。永磁同步电机的高效控制需要准确获取电机转子位置信号,然而,安装位置传感器成本较高且占用了较大体积。无位置传感器控制的应用能解决这一问题。
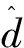
脉振高频注入法在低速带载的工况下会产生一定的位置估计误差,有学者提出这种误差是由于电感交叉耦合效应造成的[1-2]。针对这种情况,文献[1]采用有限元法获取电机交直轴增量自感及互感,从而计算误差大小。文献[3]采用预装在电机上的位置传感器与估计位置比较获得误差值。针对误差的补偿方法,大多数文献都是在估计结果中直接加上误差量进行补偿[1,3-4],然而这种方法由于交叉耦合带来的磁凸极偏移依然存在,无法得到良好的补偿效果;文献[5-6]在PI调节器前增加补偿信号,但是这种方法计算比较繁琐。本文针对这一点,提出一种新的前馈补偿方法,对交叉耦合带来的位置估计误差进行补偿,实现了较好的补偿精度。对一款48槽4对极永磁同步电机进行仿真,初步证明了该误差补偿方法的准确性。
1 传统脉振高频注入法原理
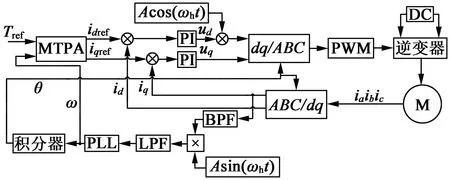
图1 传统脉振高频注入法框架图
永磁同步电机在转子坐标系下的电压方程:
(1)
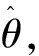
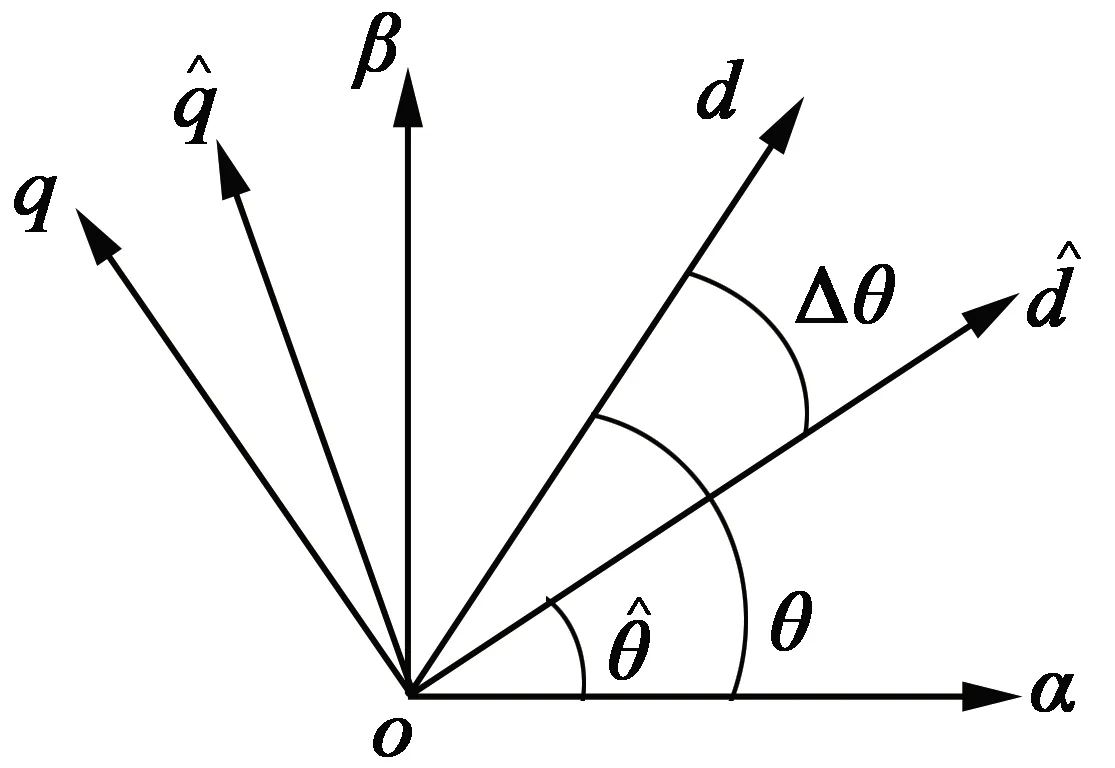
图2 高频注入法坐标分析
当估计角度与实际角度存在偏差时,根据坐标变换,电机实际旋转坐标系以及估计旋转坐标系下的电压、电流换算:
(2)
(3)
假设注入到估计的同步旋转坐标系的高频电压信号如下:
(4)
在低速环境下,电机反电动势很小,且高频下电阻引起的压降远小于电感,可忽略。高频电压模型可以表达:
(5)
转换到估计旋转坐标系,高频电流响应可以表达:
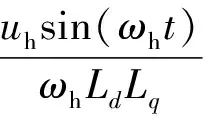
(6)
定义L=(Ld+Lq)/2,ΔL=(Ld-Lq)/2,代入上式可得:
(7)
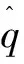
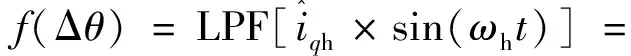
(8)
当角度误差较小时,可进行线性化,得:
(9)
将该信号经过PI控制器调节,使其收敛到零,可以使估计旋转坐标系贴合实际旋转坐标系,实现转子位置的正确估计。
2 低速无位置传感器电感误差分析
上述高频电压注入法分析将永磁同步电机简化为线性模型,交直轴相互独立,然而随着电机功率密度提升,在设计电机时常常将电机工作点设置在趋于饱和的位置。电机磁路饱和时,交直轴存在共磁路的位置,会产生交叉耦合效应,反映在交直轴互感上。考虑交叉耦合效应时,电感矩阵可以表达:
(10)
根据该电感矩阵进行计算,高频电压注入下的交轴电流响应:
(11)
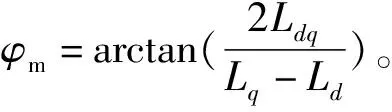
3 电机增量电感提取
由前面分析可知,无位置传感器估计误差与电机电感有关,误差的计算是准确获取电感信号。
如图3所示,对于电机饱和特性的描述,可采用增量电感和视在电感两种形式。LApp为视在电感,表示在工作点A时,ψ与i的比例关系;LInc为增量电感,表示在工作点A时,ψ与i的导数关系。高频注入法检测的是增量电感,下面通过有限元法进行电感提取。
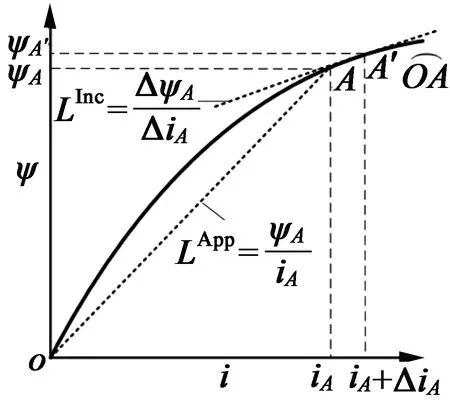
图3 增量电感与视在电感关系图
实验电机为一台48槽4对极内置“V一”型永磁同步电机。

图4 电机二位平面图
利用Ansoft Maxwell软件进行分析处理,按照实际尺寸构建电机二维模型,针对一个电角度,进行空载以及带载两种工况的分析。
根据增量电感的定义,电感提取的过程如下式:
(12)
电感提取结果如图5所示。
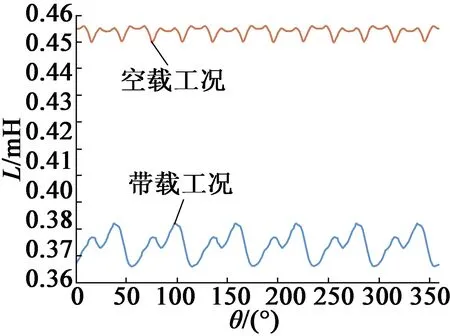
(a)单周期交轴电感分布
由仿真可知,电机带载时,交轴和直轴电感下降,交轴和直轴互感上升,因此可以解释带载时估计误差的增加。
4 误差补偿方法
对于误差的补偿,本文提出采用增加前馈补偿信号的方式进行误差补偿,使得PI调节器后能得到较为准确的结果。
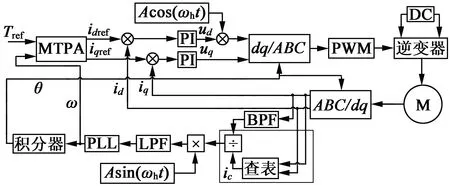
图6 改进误差补偿框架图
设增加的补偿扰动信号:
(13)
根据式(11)可知,带通滤波后的反馈电流信号:
(14)
经过正弦调制后,反馈信号加上补偿信号:
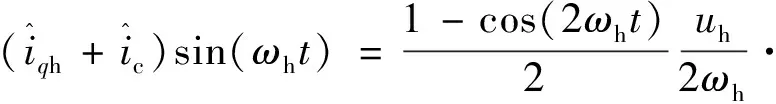
sin(2Δθ-φm)+
(15)
经过低通滤波器,可得误差信号:
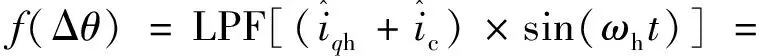
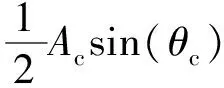
(16)
因此,补偿扰动的幅值、相位:
(17)
当Δθ趋向于零时,反馈信号值趋向于零,因此可以得到正确的位置估计,补偿了交叉耦合带来的位置估计误差。
5 仿真分析
为了验证本文误差补偿方法的有效性,本文设计仿真模型进行分析。控制开关频率为10 kHz,注入信号频率为1 kHz。仿真模拟电机运行转速为3 rad/s,对电机进行转矩控制,分别针对空载工况和带载工况进行分析。空载时,仿真结果如图7、图8所示。
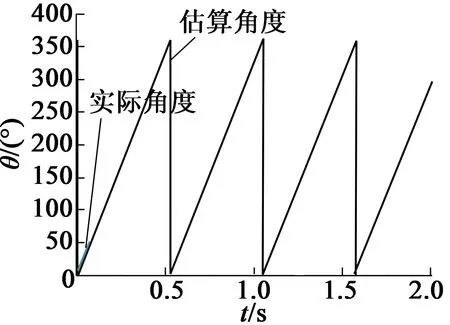
图7 空载估算角度与实际角度
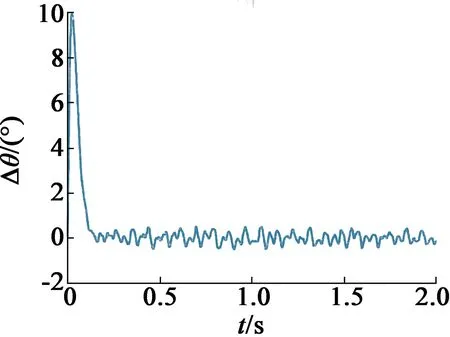
图8 空载位置估计误差
由仿真可知,空载时使用传统脉振高频注入法具有较高的位置估计精度,这是由于空载时交叉耦合现象不明显,d,q轴互感较小。
带载时,仍使用传统脉振高频注入法,结果如图9~图10所示。
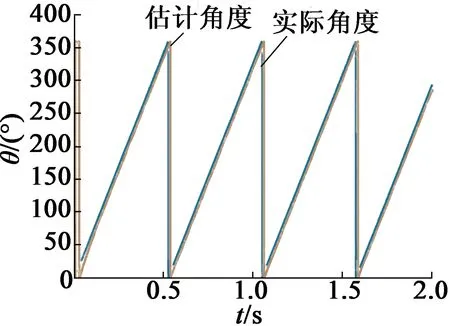
图9 带载估算角度与实际角度
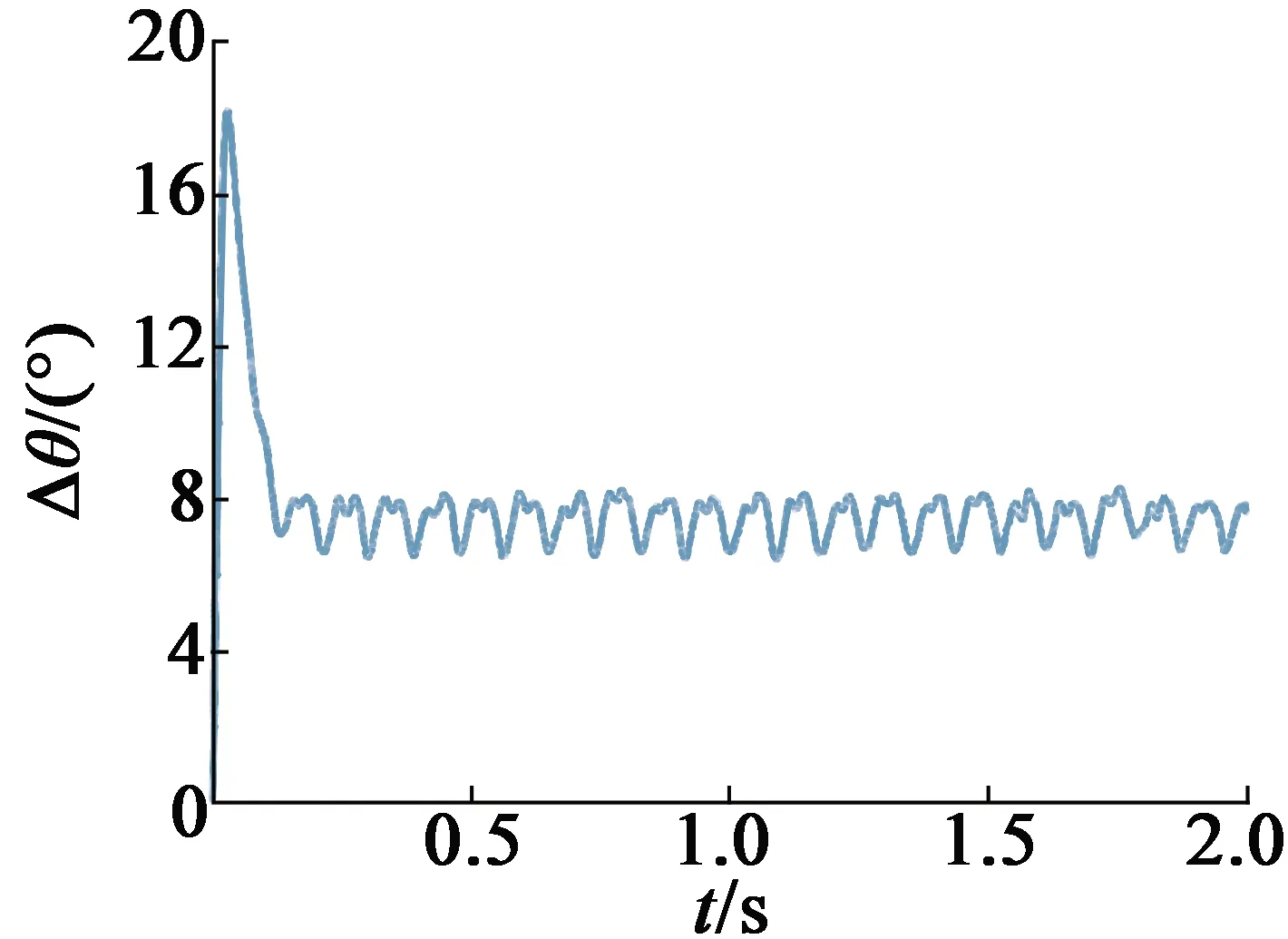
图10 带载位置估计误差
由仿真可知,当电机带载运行时,出现了8°左右的位置估计误差,与式(11)计算结果相符。
根据本文的补偿方法,根据式(17)设计补偿信号进行误差补偿,得到如图11、图12所示的仿真结果。
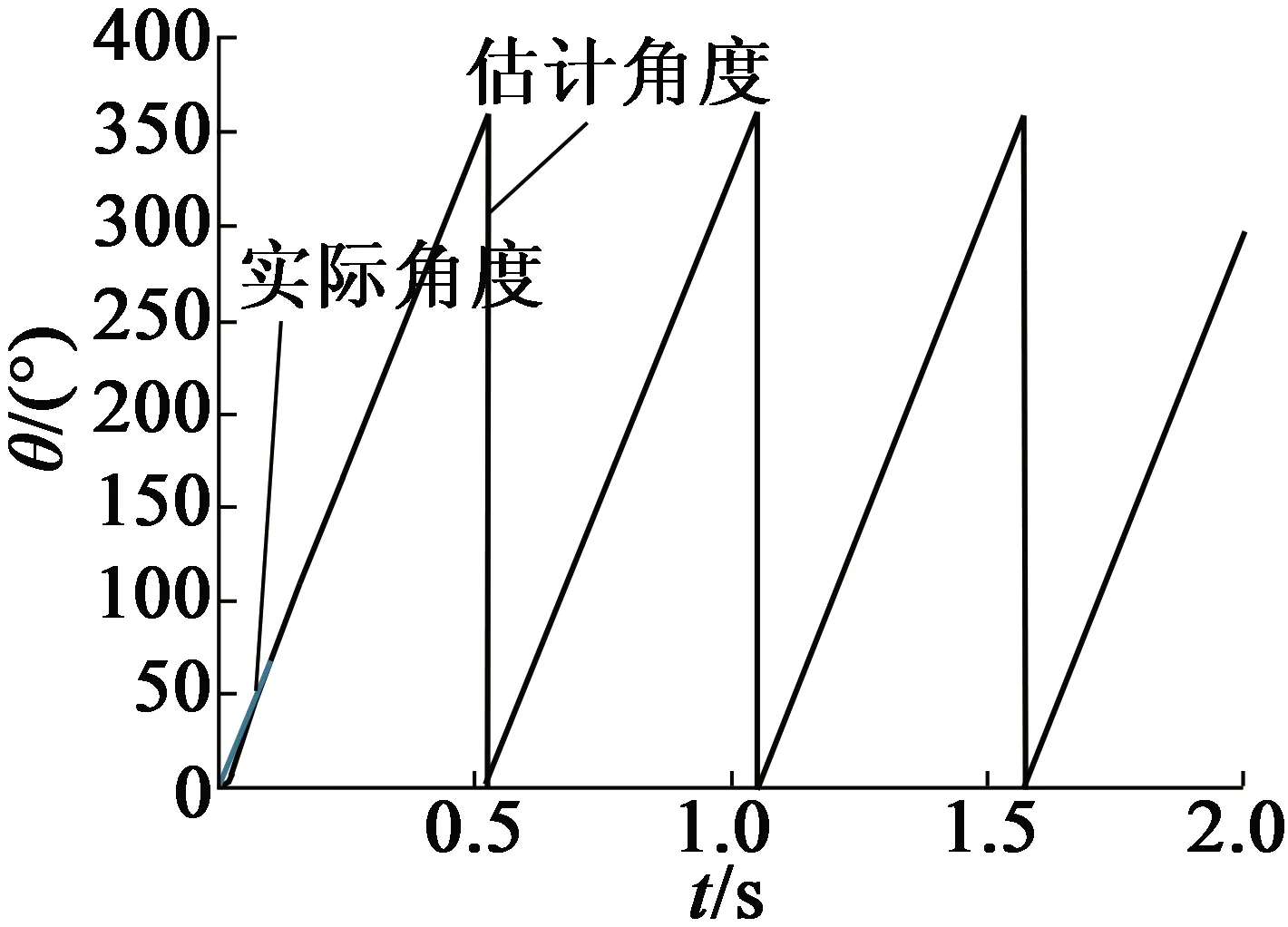
图11 补偿后带载估算角度与实际角度
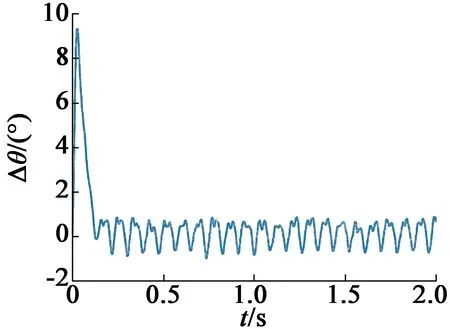
图12 补偿后带载位置估计误差
可见,该补偿方法能较好地提高位置精度,使得位置估计误差在1°以内。由式(17)可知,补偿信号幅值与高频注入电压幅值和频率有关,为验证补偿公式的准确性,将注入电压幅值增大一倍,三相电流响应如图13所示。
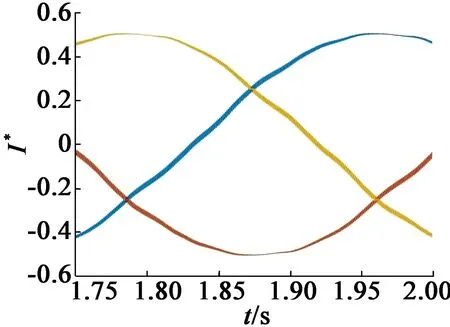
(a)原三相电流局部放大
在原补偿信号下,误差角度如图14所示。
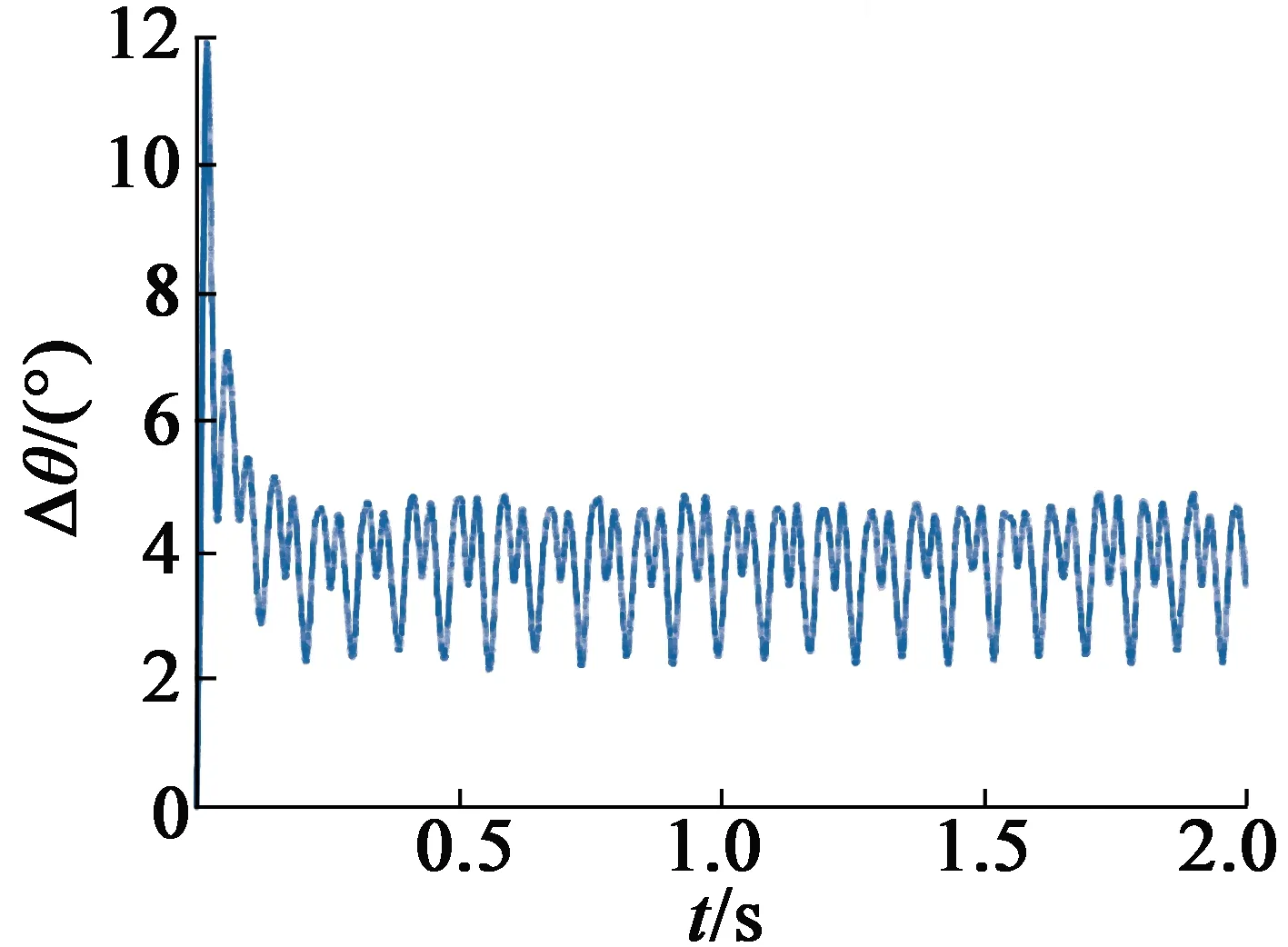
图14 改变注入电压幅值后带载位置估计误差
同样,将补偿信号幅值增大一倍,其误差角度如图15所示。
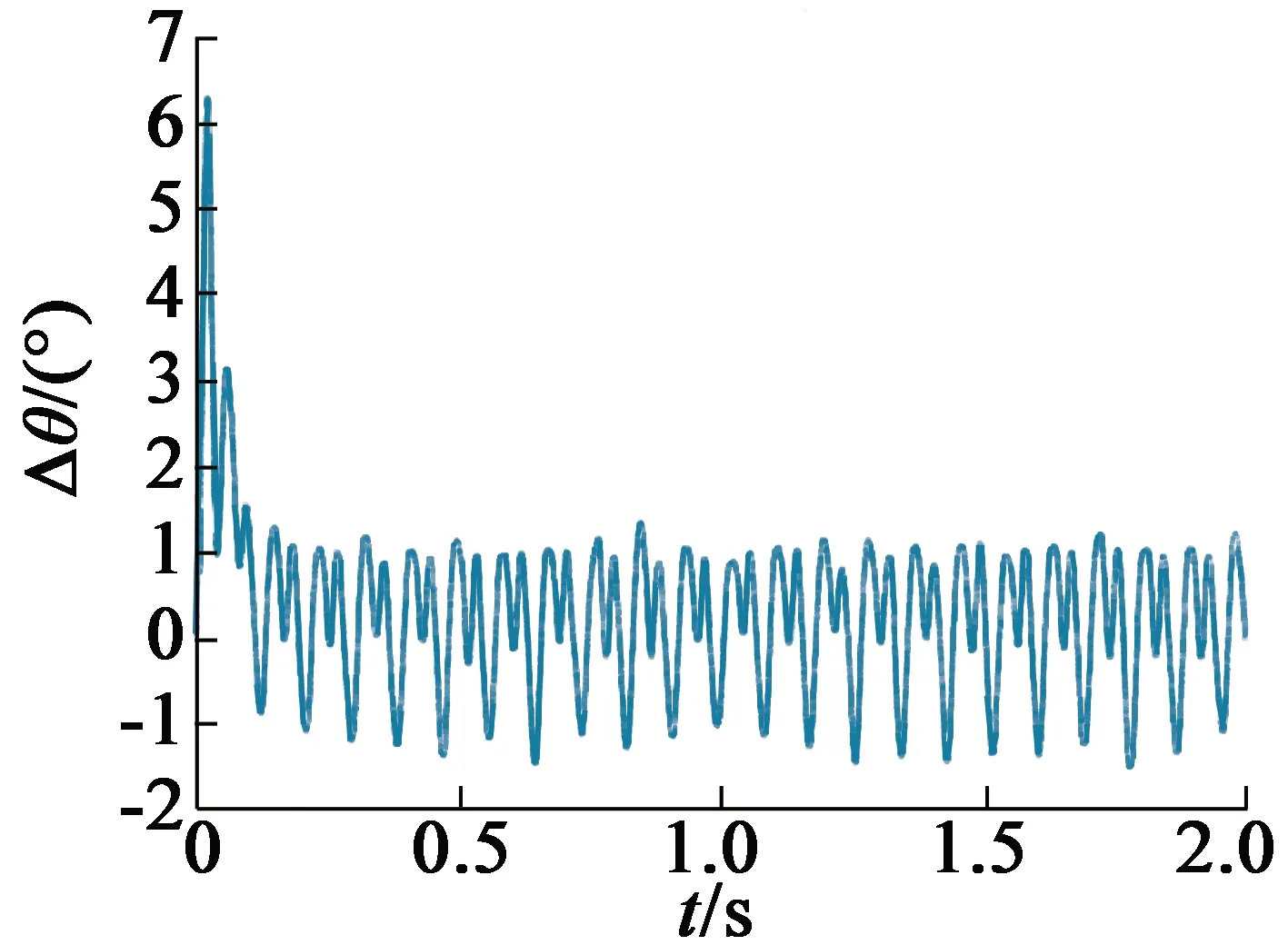
图15 改变补偿信号幅值后带载位置估计误差
仿真验证了补偿信号幅值与注入电压幅值的正比关系。更改注入电压频率也可得到类似结果,因此可以证明补偿信号公式的准确性。
6 结 语
本文研究了永磁同步电机脉振高频注入法由电机交叉耦合效应带来的位置估计误差,并针对该误差,提出采用增加补偿信号的方法进行补偿。仿真结果表明,该方法能有效降低电机由交叉耦合带来的位置估计误差,从而提高电机无位置传感器控制位置估计精度。
