基于收益管理理论的门诊预约存量控制研究

梁 峰，王玉聪，杨力萌，陈伟涛

(南开大学 商学院，天津 300071)

0 引言

门诊预约机制能够帮助医疗服务系统实现合理的资源组织与顺畅的服务流程，大大减少患者的等候时间，实现患者满意度和医院运作效率的共同提高。预约机制强调的主要是资源分配问题，即在提供的医疗资源数量一定的情况下，确定预约挂号、当日挂号和急诊的资源分配方法。对于医疗系统来说，资源的优化配置方法是非常重要的，因为分配的结果会直接影响到医疗质量、医疗成本和患者满意度。由于国内的医院人流量大、外来患者多，必须为当日挂号的门诊患者保留一定的服务能力。另外，由于国内的门诊预约服务推行时间不长，患者的预约诚信意识有待加强，尤其是在副主任医师和主治医师的预约过程中，爽约率在部分医院甚至达到了30%，因此还必须在计划阶段即开始考虑爽约率对于医疗服务系统的影响。

目前国外大部分关于门诊预约的研究主要是预约系统的设计，如门诊开始时间、门诊时间段(Time Slot)、以及每个预约时间段应安排的病人数等[1～7]，也有不少对于如何调节患者需求与医院门诊供给之间的关系研究。收益管理作为一种调节客户需求与资源供给关系的资源优化分配理论，已经较为成熟地应用于在航空业、酒店行业等领域[8～11]。通过分析易逝品的特点和收益管理的适用条件，可以将收益管理应用于门诊预约，收益管理的主要内容包括定价策略、精确预测以及存量控制等，本文主要从存量控制角度进行分析。医疗行业不同于航空业、酒店行业等行业，其具有特殊的服务性质。航空业和酒店行业每少卖出一个舱位或者客房，损失为一个票价数或订房价，而对于门诊预约，损失为医生的空闲时间所对应的成本；航空业、酒店行业每超售一个单位的舱位或客房，损失为赔偿给客人的票价或住宿费，而对于医疗行业，超订则意味着医生和护士等员工的加班成本增加。

本文基于收益管理的理论及方法，构建了医院门诊预约存量控制模型，在考虑爽约率及超订策略等因素下构建了预约存量控制静态和动态模型，分析得出允许预约的最大患者数量，以此平衡医院收益和患者满意度，并用实例说明了所设计机制的合理性和有效性。

1 收益管理应用于门诊控制的可行性分析

国外曾经有部分学者研究了收益管理在医疗服务业中的应用方法，且取得了一些成果[8,9]，国内的研究者也做了相应的研究探索[14～16]。过去由于国内外医疗体系结构及相关政策的差异，成熟的收益管理相关理论及方法无法直接应用在我国的医疗体系中。尤其是我国的医院门诊价格相对固定，且差距不大，医院在进行决策时无法采用常规的成本作为优化目标，很难将存量控制应用到门诊预约中。然而，新的医改政策的颁布，为收益管理在医院门诊预约的应用带来了契机。新的医改方案推行医药分离、分开核算，取消药品顺价加成销售，若要达到收益最大，提高医疗服务收入显得尤为重要。目前国家正在全面推开公立医院改革试点工作，通过调整医疗服务价格结构，实现由“以药养医”向“以医养医”的转变，在试点医院调整现有的医疗服务收费价格体系，未来的门诊价格将大幅提高，并形成阶梯式的服务价格，使医生的服务得到应有的价值体现。目前全国大部分城市都取消了药品加成，而提高了医事服务费的价格。这些改革方案为收益管理在医院门诊预约中的应用提供了有利的条件。

Kimes等人提出了收益管理理论的6种行业应用特征[17]，结合医院具体的特点，对医院运用收益管理理论的可行性分析如下：

(1)产品或服务具有时效性。医院不可能将今天没有使用的医护服务进行储存并提供给第二天后面的患者，也就是说，如果某个时段，医护人员并没有把服务提供给患者而使其处于闲置状态，那么就意味着医院丢失此次可以创造收益的机会。医院的一些医疗设备，如CT等，的使用也一样无法被储存。正因为这些产品具有易逝性，医院只能尽量提高使用产品和提供服务的效率，从而实现较大的收益价值。

(2)相对固定的生产能力。一家医院医护人员可以提供的服务量是固定的，如可为病人看病的医生数、可服务病人的护士数等，这些人员都不可能在短时期内增加，要想提高医院服务容量，只有通过招聘等其他环节；医院的医疗设备每天可以服务的患者数也不变；病房类似于酒店客房，数量在短期内是固定，如要建造新的病房，需要投入大量的时间和财力。综合以上因素，在未来一段时间内，医院提供服务的能力大体不变，如果在需求高峰期，医疗资源无法满足患者需求，则会丧失增加收益的机会。

(3)需求随时间而变化。医疗服务需求随时间的波动性很强，不同的季节，不同的日期，不同的时间，病人对于医疗的需求也不尽相同。因为患者需求本身就具有不确定性和季节性的波动，比如，当气温变化剧烈，流行感冒爆发时，患者对于医护资源的需求会突然大大增加；其他一些特殊疾病和传染性疾病的爆发，也会引起需求的陡然上升，因此，平缓医疗市场需求不确定性，采用存量控制策略来平衡高峰期和低峰期各个时期的供需变化十分重要。

(4)固定成本高而可变成本低。医护人员医疗服务的固定成本主要是他们高昂的薪资费用，他们在为患者提供医疗服务时，几乎不产生变动成本。医疗设备、病房等也类似，前期的建设投资十分高昂，建成之后，变动成本就较低。只要患者愿意就诊，并且支付的价格略高于管理成本，医院就可以从此次接受病人中获利。

(5)可细分的市场。患者对于价格、时间、服务等的敏感程度是不同的，因此可以根据这些将患者细分为不同的消费群体。比如公费患者和自费患者存在需求差异，前者主要考虑服务的优质性，对价格不敏感，而后者则将价格作为主要考虑的因素。医院市场患者的划分十分细致，有研究将它分为经济费用敏感性、利益优先性、随意性等各种不同的客户，根据不同的患者需求提供不同的医疗服务。因此，对不同需求层次的患者采取不同的资源分配以及价格控制策略，是解决潜在收益损失和医疗资源闲置浪费的有效途径。

(6)产品/服务可以预订。医护人员提供的医疗服务是可以提前预订的，目前已经有很多医院提供了专家门诊的网上预约、电话预约等服务，病房的使用也可以通过类似于酒店客房的方式进行提前预订。但是其他行业可以通过调控价格进行对需求的控制，而医疗服务价格一般是相对固定的，故医院收益管理的问题主要是存量控制上的研究，并且在考虑预订问题的时候应该多考虑取消预订和采取超订策略的问题。

从理论上说，在门诊服务中应用收益管理的理论和方法是可行的。国外已将广泛应用于航空领域的收益管理理论引入医院门诊预约当中， 但医院与航空领域的巨大差异导致了收益管理在医院门诊预约中的应用更为复杂。如何在收益管理应用过程中将医院的特有属性考虑进去，使收益管理与医院管理更有效地结合是一个难点也是热点问题。

此外，在医改进行前，专家资源和普通资源价格差异不大，一般多在十元左右，这时对于医院来说，对预约机制的研究意义不大。但是随着医改的逐渐深入，尤其是取消了药品加成以后，在部分医院，专家门诊和普通门诊的价格差异甚至达到了百元左右，这时预约机制的设计和优化就变得尤为重要。

2 基于Littlewood二级分配模型的存量控制基础模型

对于医院来说，存量控制，就是如何合理地分配医疗资源，从而达到医患收益最大化；医院门诊预约，则是如何限制患者的预约数量，如何合理地分配专家门诊和普通门诊之间的患者预订限制。存量控制最先起源于Littlewood提出的二级分配模型[18]，分为嵌套机制和非嵌套机制。嵌套机制是指具有较高价格的需求类型可以有限占用较低价格类型产品的预留量；非嵌套控制机制是指各种价位的产品进行独立的分配，分别为每种产品设置预订限制。考虑到未来医院的营收基本上是以医生的医事服务费为主，而且公立医院必须坚持公益导向的管理方向，当出现患者受限于专家门诊的高诊疗价格，而大量预约普通门诊的情况时，医院依然存在着将部分专家门诊转化为普通门诊的内在动力和外在要求，本文考虑的是允许专家门诊向普通门诊转化的嵌套机制。

存量控制模型给出以下假设：

(1)假设患者需求是普通门诊需求先到达，专家门诊需求后到达。在实际中，医院的专家门诊基本上是全预约制，所以专家门诊的患者会根据预约时间准时到达，而普通门诊患者会提前到达，以确保可以在当日就诊。

(2)普通门诊需求和专家门诊需求各自的患者预约请求是相互独立的变量，且需求量与存量策略无关。

(3)不考虑爽约的情况。

(4)不会出现一个患者一次性同时预订多个服务的情况。

(5)各个价格等级的患者不会出现需求转移的情况。

(6)各个患者到达彼此相互独立，不受其他患者的影响。

假设医院普通门诊数量供不应求，而专家门诊仍然有空余时，会有一部分专家医生以普通医生的价格为患者提供医疗服务，从而进一步增加医患收益。由于患者收益涉及消费者剩余价值理论，患者对诊疗价格的满意度水平受其对于价格的敏感度影响，为简化模型，这里不考虑患者的收益，医院的收益通过预约价格进行衡量。

本节采用Littlewood二阶段分配模型来建立门诊预约挂号医生存量控制模型。

模型参数定义如下：

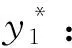
假设专家门诊为产品1，普通门诊为产品2。根据Littlewood法则，如果把专家门诊的空闲医生以普通门诊价格销售所得的医院收益，大于专家门诊以原价位出售时医院收益的期望值，则可以选择降价售出该专家门诊号，否则就不出售。

因此可以得出：

(1)

暂且不考虑患者的收益，则患者选择某种门诊后医院的收益即为患者的挂号费用，则模型转化为：

(2)

这里只需要通过数据调研分析专家门诊的需求服从何种分布，从而进行计算，得出专家门诊最优预留量。上述问题得到的是正常情况下的静态预约存量模型，如果医院对于爽约率带来的收益损失不敏感，可以直接应用到医院的门诊实践中。如对于北京等地的大型三级甲等综合医院来说，首先并不介意由于爽约带来的收益损失，其次在这种类型医院中，其爽约率非常低，可以忽略不计。但是对于大部分医院来说，尤其是一些专科医院和三级乙等以下的综合医院，其爽约率会直接影响到医院的收益，如果可以采用超订的方式来减少病人爽约带来的收益损失，就必须要建立超订情况下的医院门诊预约存量控制模型。

3 基于超订策略的预约存量控制模型

假设医生每天最大的可服务的病人数量为C，医院提供预约服务的价格为f，截止就诊时间前医院提供病人预约的服务数量为m，提供服务当天没有出现的患者数量为k。由于医院不同于其他服务行业，预约后无法拒绝病人就诊，则当超订导致实际到达顾客数量超出了医院能够提供服务的最大数量时，医院因超订带来的成本增加损失为b，医院收益为R。假设每位患者预订后实际到达概率均为p，设Pk为k个患者爽约的概率。

那么在医院提供该项服务的当天，实际到达的患者的数量为m-k，则当天医院收益为:

(3)

医院所获利润应该为期望利润，设为L

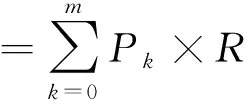
(4)

整理得：

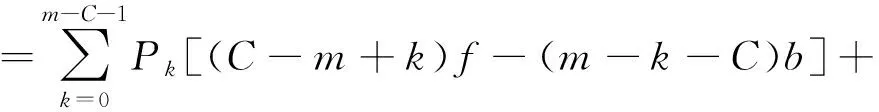
(5)

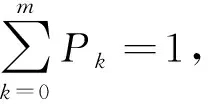
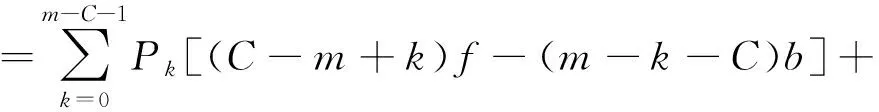
(6)

患者未到达事件属于偶然事件，如果患者全部到达，没有预约患者未到达的情况，则有:P0=1,Pk=0,带入上述公式，化简得:

L=mf-(f+b)(m-0-C)=Cf-b(m-C)

(7)

由此可见，医院总收益Cf减去因实际到达患者过多导致的损失b(m-C)，即为医院的净收益。当m=C时，就是供需达到平衡，此时医院可达到最大利润，且病人满意度也较高，这与实际情况是相符的。

对于非特殊情况，存在患者预约后未到达的情况时，那么上述问题演化为如何确定Pk值，即k个患者没有到达的概率。模型假设各个患者是否到达相互独立，则会有二项分布Pk～B(m，1-p)

(8)

(9)

代入式中得：

(10)

由于参数f，p，b，Pk，C都是可通过调研确定的，且具体数值不受控制，则医院能控制的变量即为总的超订下的服务能力m。确定参数f，p，b，Pk，C以后，需要计算最优m*值使得公式中L最大。

4 算例分析

4.1 算例简介

根据调研结果，天津T医院诊室预约挂号类型一般分为普通门诊预约和专家门诊预约，专家号价格为120元/人，普通号为20元/人。医院按照“先到先得”的原则分配号码源，当已预约号码量少于预约限制的时候，如果有新的患者需求，那么将剩余的号源分配给患者；当预约号码量达到限制的时候，如果仍有新的患者需求，则按照紧急程度推荐转院或者安排预约第二天就诊。

医院采用的号源分配方式只考虑了单类医生医疗资源价值的最大化，没有考虑医生综合价值的最大化。事实上，“先到先得”分配原则在某些情况下并非最优。由于专家门诊和普通门诊的需求有较大差异，在对待普通门诊患者时，医生的诊断服务水平基本相同，因此医院可对医生进行综合管理，用医生总数对预约存量进行控制。医院可以在普通门诊无号源而专家门诊仍有空余的情况下，使一部分专家门诊医生以普通门诊医生的价格为患者提供服务，可以运用第三节建立的存量控制模型来进行计算，确定最优的预约存量，以决定保留多少专家门诊预约号，使医院收益最大。

4.2 基础算例

通过调研，我们得到T医院2016年1月～3月中专家门诊每天的需求量。通过Excel表格统计分析，得出90天内对于专家医生的需求量，近似取每个专家医生每天可以服务的病人数为30个。对统计得出的病人数量进行处理，得出专家医生的需求数，根据样本数量进行频次统计分析得出表1，再分析得出需求分布函数。

表1 专家门诊每日需求数量分布

从所得的数据可以得知，专家门诊每日需求分布主要在1到8这几种情况，并且需求分布是离散型的，我们假设需求服从泊松分布。由于样本容量较大，因此不适合采用K-S检验分析拟合度，采用二次方检验拟合得出统计检验结果的p值大于0.05，假设合理。因此，假设D1服从参数为3.7的泊松分布。

根据以上的调研数据，带入具体的分布参数值，可以得出：

根据最优保护水平计算表，得出表 2：

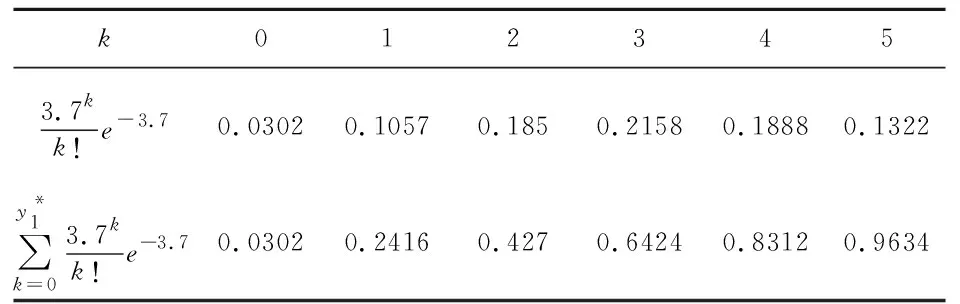
表2 数值查询计算

4.3 考虑超订的存量控制算例

以T医院内科诊室为例，考虑到门诊的普通医生除了接受预约之外，还需要接受当日挂号的患者，因此即使出现爽约的情况，也会被当日挂号的患者所使用，并不会带来收益的损失。因此本文仅研究专家医生的预约存量，这也符合医院的实际情况。T医院内科诊室每天共有8名专家医生坐诊，每位专家医生每天可服务20位病人，则该诊室医生每天可服务病人数量为160人，医院提供预约服务的价格为120元/人，医院截止就诊时间前医院提供病人预约的服务数量为m，提供服务当天患者没有出现的数量为k。考虑到超订后如果接诊患者，则会带来医生的加班成本，而不接诊则是失销成本及患者满意度的下降成本，因此定义因超订带来的成本损失为180元/人，医院收益为R。p为每位患者预订后的就诊概率，为k个患者爽约的概率。

调研T医院2016年3月1日到3月20日的患者就诊情况，统计结果如表3。

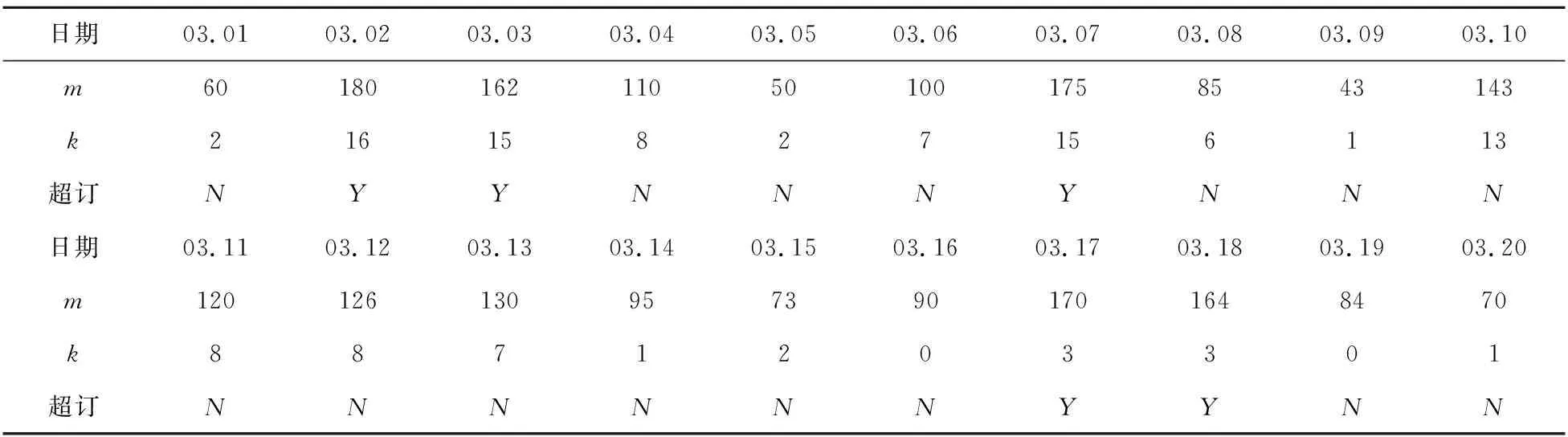
表3 患者爽约情况调查表

每天的m数量变化较大是因为8位医生属于内科的四个不同科室，分别为呼吸内科、消化内科、心血管内科和神经内科。其中呼吸内科和消化内科的整体实力很强，因此预约量整体较多，而心血管内科和神经内科只有个别还价医生实力较强，所以预约量不稳定，基本上取决于实力较强的专家医生当天是否出诊，另外考虑到周初和周末就诊人数的差别，最终形成整个内科的预约量有较大的变化。

由于医院收益函数为:

由上述公式可以得知每日医院收益如表4，收益的变化如图1所示。

由上述公式可以得知每日的医院收益如表4。

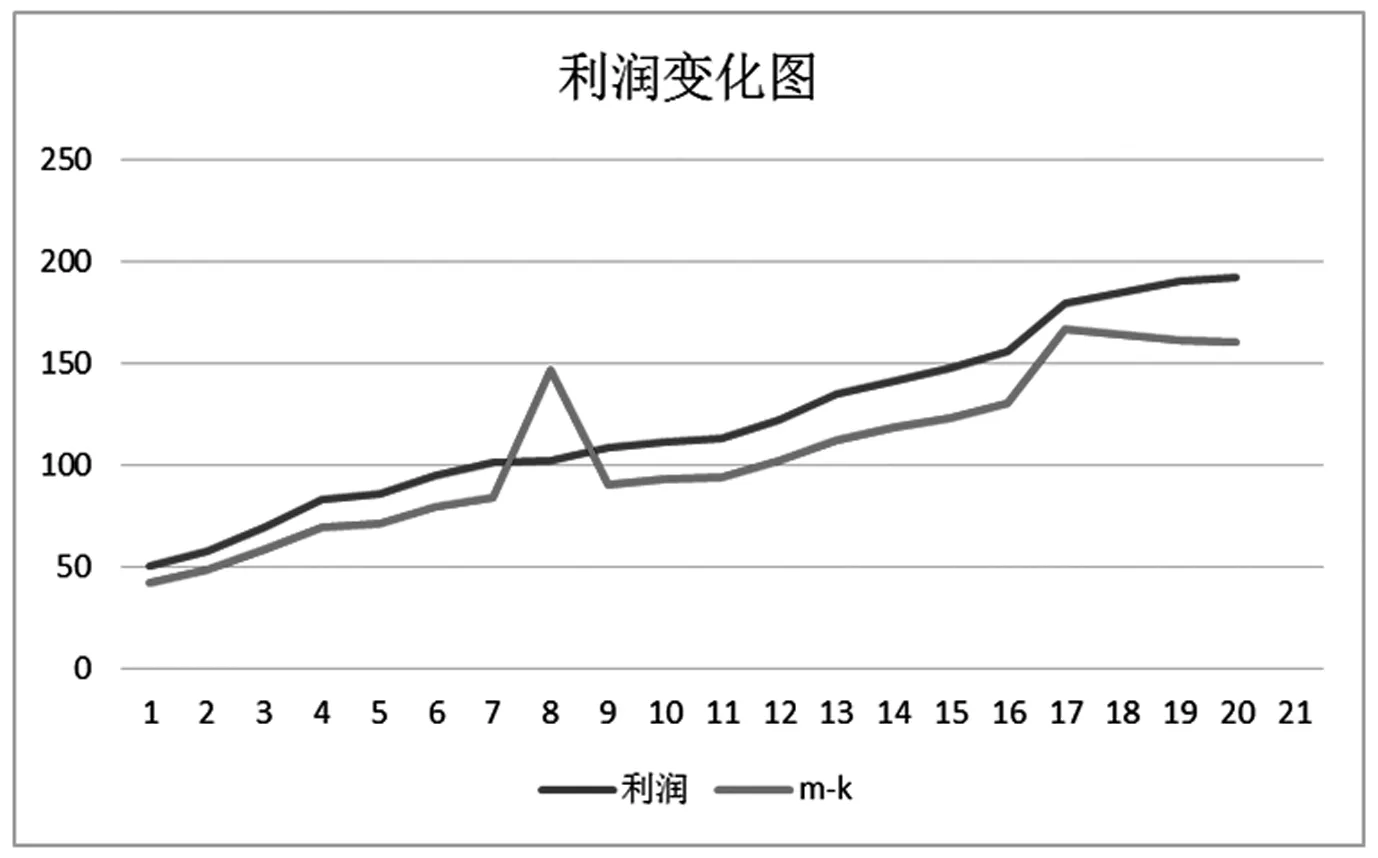
图1 医院收益变化图

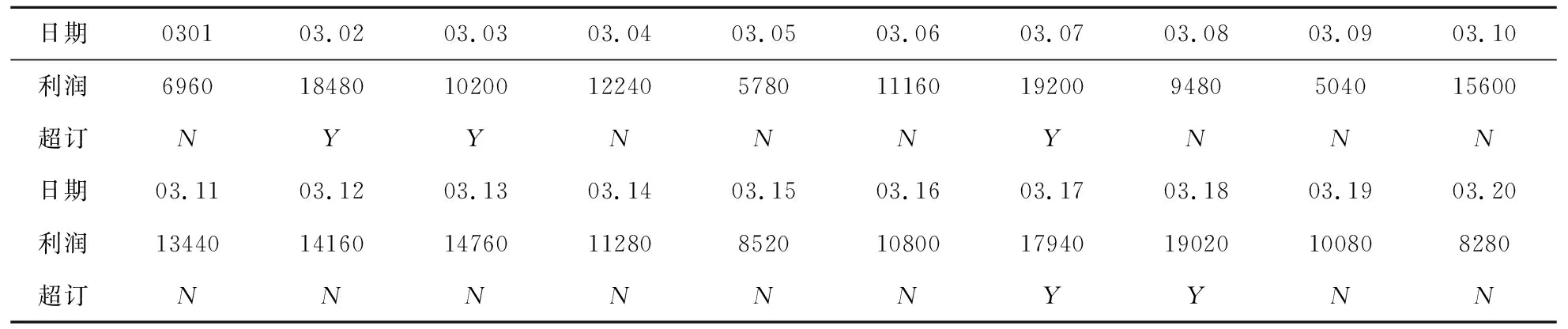
表4 研患者利润结果表

由此表可以分析得到，当预约人数和爽约人数之间的差值接近最大存量时，医院的收益最高，当远离最大存量时收益会越来越小。如对于03.07的门诊预约情况，预约人数为175，爽约人数为15，预约人数减去爽约人数为160，利润最大为19200。而对于03.17的门诊预约情况，预约人数为170，爽约人数为3，预约人数减去爽约人数为167，超订7人，利润为17940。而未超订时，随着预约数量的增加，利润逐渐增加。

根据公式(10)可得医院净收益为：

(11)

(12)

通过调研分析可以确定参数f=120，p=0.9，b=180，C=160，基于公式(12)可以求解出当m=168时，L=20100最优，超订人数最大可以达到8人。

4.4 超订模型与排队论模型的验证分析

基于以上的数值实验，采用超订模型与排队论模型进行分析对比。把患者预约过程看作一个排队过程，专家门诊的预约挂号过程可以模拟成M/M/1/N/∞排队系统。若患者预约成功，预约系统得到收入，患者离开系统(取消预订)，就产生退款。则该超订模型的假设条件为：

假设1患者需求是无限的。

假设2预约取消率服从参数为的负指数分布。

假设3患者预约请求是独立发生的。

模型参数如下：

C：医院医生每天最大的病人服务数量;λ：患者到达率，服从泊松分布;f：提供预约服务的挂号价格。假设只有一种服务类型，价格都是一样的;Lq：队长。是排队系统中已经接受的平均患者数量(取消预订的已经除去);N：系统存量限制，即最大预约量的限制;H：超订引起的损失成本函数。

当超订导致医生无法在值班时间完成就诊时就会进行加班，将加班成本作为超订引起的损失成本，假设医生给x位超订患者服务引起的成本是F(x)，则

(13)

假设取消预约或no-show的患者可以获得全额挂号费用退款，那么医院预约系统收益函数为：

L=fLq-F(Lq-C)=fC-[F(Lq-C)-f(Lq-C)]

(14)

因为超订导致医生平摊给一个患者的加班成本大于接受一个患者预约的挂号费，则F(Lq-C)>f(Lq-C)。因此可以得出当Lq=C时，收益最大。

(15)

通过以上分析可以看出，对于排队论模型来说，当ρ值很大时，超订量近似为1，而当值逐渐变小时，即预约取消率越大，超订量就越多，这与本文所提出的超订模型是相符的，也符合实际的情况，即超订策略就是为了防止因为预约取消或爽约带来的医疗资源的空闲。

5 总结

论文分析了收益管理在在医院管理上应用的可行性，利用收益管理的理论和方法构建了医院门诊预约存量控制的基本模型，并将爽约的情况和取消预订的因素考虑进去，建立了超订下的单级价格医院门诊预约存量控制模型，算例证明了所提出方法的有效性。未来可以在针对门诊存量的动态控制、考虑医院和患者共同收益的存量控制等方面继续展开研究。