基于Copula的供应链金融质物组合价格风险测度研究

胡海青，陈 迪，张 丹,2，张 琅

(1.西安理工大学 经济与管理学院，陕西 西安 710054； 2.西安交通大学 经济与金融学院，陕西 西安 710061)

0 引言

供应链金融作为“物流与金融的创新服务模式”，为中小企业的融资提供了极大的便利。供应链金融中的保兑仓融资模式与存货质押融资模式是一种以原材料、半成品以及产成品等存货作为质押担保物来降低和规避贷款风险的业务，质物价格的变化会影响其在未来融资期限内担保能力的变化，特别是价格的极端波动，因此准确度量质物的价格波动风险是保障供应链金融融资业务持续健康发展的前提。由于商业银行在开展供应链金融业务时主要以单一质物为主，因此国内外的研究主要集中在单一质物价格风险的测度，随着供应链金融业务的不断发展与完善，商业银行为了增加业务的吸引力与灵活性，开始逐渐对多种质物构成的质物组合进行质押，所以质物的多样性对商业银行的价格风险管理提出了更高的要求，不同质物间价格波动的相关性对价格集成风险测度的影响也不可小觑。同时现有集成风险测度方法多以金融资产的线性相关关系为基础，而存货等质物的收益率具有“尖峰厚尾”特征的事实表明其并不服从正态分布，并且多数质物价格间存在非线性相关关系，因此需要引入一种新的理论方法来刻画质物间的非线性相关性。此外，与股票、债券等金融资产相比，存货等质物的流动性较弱，从风险识别到风险处理期间的期限较长，因此对供应链金融质物组合的价格风险决策在于长期价格风险预测。基于以上分析，如何在质物多样化与市场复杂化的背景下，考虑不同质物价格波动之间的非线性相关性、极端性以及长期性，对商业银行供应链金融质物组合的价格风险进行风险集成测度值得深入研究。

基于此背景，本文从商业银行的角度出发，在考虑质物组合间价格波动的非线性相关性，兼顾极端事件发生的基础上，引入Copula函数和CVaR模型，构建质物组合长期价格风险度量模型，量化分析供应链金融质物组合的长期价格集成风险。该研究为学者们研究供应链金融质物组合的价格风险提供了新思路，同时丰富并完善了供应链金融管理与风险管理等相关理论体系。

1 文献回顾

由于质物的价格风险主要存在于供应链金融中的保兑仓融资和存货质押融资业务中，因此本文主要从这两个业务入手，对供应链金融价格风险相关文献进行回顾与梳理。关于供应链金融价格风险防范与控制，现有文献基于定性研究和定量研究两方面认为可以通过风险控制直接工具(利率和质押率)、契约设计机制和产品定价等方式来实现。国外的Cossin和Hricko[1]等学者在企业信用风险与质物价格波动存在相关性的基础上，定量研究了具有价格风险的质物的定价问题。Buzacott和Zhang[2]最早提出可以将企业的库存量与存货质押融资业务模式下的贷款额度结合起来，以此对商业银行的风险进行有效管理。弯地红[3]以应收账款融资模式为例，认为现有的供应链金融风险规避机制不够完善，应在商业银行与大型核心企业之间建立一种新的合作关系。李毅学[4]在考虑我国金融创新下存货质押融资业务的环境和特征后，设计了相应的业务合约条款、关键风险点及其控制指标。同时多数学者将对价格风险的探讨包含在质押率问题的研究中，李毅学等[5]运用风险评估模型的“主体+债”评估策略，对有关价格随机波动的存货价格问题进行了研究。黄云飞等[6]以钢材为研究对象，采用历史模拟法研究了钢材存货质押业务中的质押率问题。

在上述研究中，学者们从不同角度探讨了如何规避供应链金融业务的价格风险，然而却未直接对价格风险展开定量测度。精确测度质物价格风险是有效地控制和防范供应链金融价格风险的前提，鉴于此，国内外学者对质物价格风险测度进行了相关研究。如国外学者He等[7]以钢材为例，应用VaR方法研究了质物钢材的价格风险。胡启帆[8]采用历史模拟法对现货铜的价格风险价值VaR进行了测度。何娟和蒋祥林等[9]构建了VaR-GARCH模型对质物钢材的价格风险进行了测度，并认为该方法比历史模拟法精确度更高。唐少麟等[10]、孙元花[11]分别将VaR理论应用到仓单质押风险与质物铝价格风险测度的研究中，为商业银行开展相关质押业务提供了科学依据。不难看出，上述学者主要选择VaR来度量供应链金融存货质押融资业务的价格风险，尽管VaR已经成为测度金融市场风险的主流方法，但是还存在很多不足。对VaR的争议主要集中在VaR不能充分地预测极端情况，如McKay和Keefer曾研究得出VaR并不能反映类似“美国1987年股灾”这样的金融市场极端情况。据此，学术界提出了用CVaR测度风险，Rockafellar和Uryasev[12]率先提出了CVaR的概念，认为CVaR是在一定持有期内，风险值超过给定置信水平下的VaR的平均损失。王娜等[13]在采用VaR和CVaR方法测度我国开放式基金绩效时，通过返回性测试发现基于CVaR方法更能够提高风险测度的精确度。随着学者们研究的深入，少数学者开始将CVaR应用于供应链、供应链金融领域中，李夏[14]构建基于CVaR的供应链风险评估模型，对供应链综合风险进行了评估。何娟、王建和蒋祥林[15]将CVaR方法应用到质物价格风险中，为研究供应链金融质物风险开辟了新思路。

关于供应链金融质物类型的研究，现有文献主要以单一质物为主，而商业银行在开展供应链金融业务时，会面临选择由多种质物构成的质物组合，因此商业银行更应该关注质物组合的整体风险，而不是单一质物的风险。如果将单一质物的价格波动作为一个风险驱动因子，那么质物组合的价格风险将是所有单一质物风险驱动因子的共同作用，并且这些单一风险因子并不孤立，存在一定的相关性。因此可将金融资产的集成风险引入到供应链金融质物组合的风险测度中。总体来看目前对于集成风险的研究还处于起步阶段，传统的集成风险测度方法认为风险因子之间存在线性相关的关系，集成风险的大小就是单一风险的简单加总。Rachev et al.[16]曾系统地阐述了用线性相关系数来确定金融资产之间相依性所存在的缺陷。大量研究表明单个金融资产收益率分布具有“尖峰厚尾”的特征，并不服从正态分布。显然传统的集成风险测度方法违背了非线性相关的事实，从而高估或低估整体风险，导致风险资本的不合理分配。而Copula方法与理论可以较好地度量风险因子之间的非线性、非对称性的相关关系，因此基于Copula函数的风险度量模型得到了国内外学者的高度关注。国外学者Dias et al.[17]利用Copula模型研究了不同类型汇率间的相依关系，研究结果表明Copula模型在刻画汇率间相关关系时要优于其他模型。Rosenberg和Schuermann[18]运用Copula函数对17家跨国商业银行和从事证券经营的金融机构的三种风险进行集成测度，并与各类风险简单相加后的结果进行对比，结果表明后者会高估总体风险。刘祥东[19]、姚德权和王文进[20]通过Copula连接集成模型构建了商业银行风险集成管理框架。周孝华等[21]、陈坚[22]、苟红军等[23]将Copula模型应用到投资组合的风险研究中。近年来，学者们又将Copula函数引入到能源、供应链金融等新兴领域中，赵鲁涛和李婷[24]构建Copula-VaR模型对能源产业的投资组合价格风险进行测度研究，何娟和王建[25]将Copula函数应用到存货质押融资业务的价格风险测度中，之后何娟、王建和蒋祥林[15]通过Copula函数模型为商业银行提供了一种质物组合风险管理的新模式。

通过对现有相关文献的整理，不难发现，现有研究存在以下不足：第一，针对质物价格风险的极端情况考虑不足，然而供应链金融质物组合中的金属、能源类的质物价格与金融资产类似，具有尖峰厚尾等特征，其价格波动的极端情况才更是商业银行在开展供应链金融业务重点关注的对象。第二，现有研究考虑到供应链金融质物组合长期价格风险的较少，与金融资产相比，存货等质物的流动性较弱，从发现风险到风险处理之间的清算期较长，并且质物存在一定的质押期限，这些都表明商业银行对质物价格风险控制的核心在于预测质物的长期价格波动风险。第三，质物选取存在单一性，对单一质物价格风险研究较多，而对质物组合价格风险研究较少。

本文在现有研究基础上提出构建Copula-CVaR模型来测度供应链金融二元质物组合的长期价格风险，将CVaR与VaR测度结果进行对比，比较分析短期价格风险与长期价格风险，将Copula模型与传统风险测度方法下的风险值进行对比，以期能够保守谨慎合理地评估质物组合价格风险大小，对商业银行开展供应链金融业务的价格风险防范提供量化支持。

2 模型构建

本文构建Copula-CVaR的风险度量模型，对供应链金融质物组合的价格波动进行测度。首先估计出各个单一质物的边际分布，再结合最优Copula函数估计出供应链金融质物组合的联合分布，在此基础上运用蒙特卡洛模拟法计算短期价格风险VaR和CVaR，进而引入时间平方根法则测度质物组合的长期价格风险VaR和CVaR，为商业银行的供应链金融业务风险管理活动提供一定的决策依据。

2.1 单一质物边际分布的确定

在求出质物组合的联合分布之前需要拟合出单一质物收益率的边缘分布，目前确定随机变量的分布主要有参数估计法和非参数估计法。其中参数估计法是首先假定随机变量服从某种分布形式，如泊松分布，t分布，正态分布等，然后利用样本数据估计假定分布中的参数，最后检验其是否接受假定的分布形式。而非参数估计法事先不假定样本服从某种分布，而是基于经验分布或者核密度估计，根据样本数据将经验分布函数或核密度估计的分布近似为随机变量所服从的分布。由于质物价格波动类似于金融变量收益率的波动，往往呈现出“尖峰厚尾”特征，很难在常见的含有参数分布找到合适的分布来估计，因此本文选择利用核密度来估计三种单一质物的边际分布。

2.2 质物组合联合分布的确定

供应链金融质物组合的价格波动受多方面因素的影响，除了组合中单一质物价格波动的影响外，质物间价格波动的相关关系也是影响质物组合整体价格风险的另一重要因素。本文选用Copula函数来刻画质物间的相依关系。在计算出Copula函数的参数前需要利用K-S检验法判断单一质物的边缘分布是否服从[0,1]均匀分布。在金融相关性分析中常用的Copula函数主要有两大类：椭圆Copula族和阿基米德Copula族。其中椭圆Copula族主要包括正态Copula和t-Copula，阿基米德Copula族主要包含Clayton Copula、Frank Copula和Gumbel Copula等。二元正态Copula函数的分布函数表达式为：

C(u1,u2;ρ)=Φρ(Φ-1(u1),Φ-1(u2))

(1)

其中，u1,u2是两个金融变量，ρ是对角线元素为1的对称的正定矩阵，Φρ(·,·,·)是相关系数矩阵为ρ的标准二元正态分布函数，Φ-1(·)是标准二元正态Copula分布函数的逆函数。

二元t-Copula函数的分布函数表达式为：C(u1,u2;ρ,v)

(2)

二元Clayton Copula函数的分布函数表达式为：

(3)

其中u1,u2是两个金融变量，θ是相关参数，当θ趋于0时，变量u1,u2趋于独立，当θ趋于∞时，变量u1,u2趋于完全相关。

二元Frank Copula函数的分布函数表达式为：

(4)

其中u1,u2是两个金融变量，λ是相关参数，当λ趋于0时，变量u1,u2趋于独立，当λ>0时，变量u1,u2正相关，当λ<0时，变量u1,u2负相关。

二元Gumbel Copula函数的分布函数表达式为：

C(u1,u2;α)=exp{-[(-lnu1)1/α+(-lnu2)1/α]α},α∈(0,1]

(5)

其中u1,u2是两个金融变量，α是相关参数，当α=1时，变量u1,u2相互独立，当α趋于0时，变量u1,u2趋于完全相关。

(1)Copula参数的选择

Copula函数参数估计的方法主要包括参数法估计和非参数法估计。参数法中又包含了最大似然估计法(MLE)和两阶段估计法(IFE)，由于参数法在估计参数前需要对单一资产的边际分布进行假定，其估计效果主要依赖于变量的边缘分布函数的拟合效果，稳定性较差。因此本文使用非参数法中的核密度估计法来估计Copula参数，该方法不需要对边缘分布进行先验参数假定，Copula函数参数估计的精度较高。

(2)最优Copula函数选择

(6)

2.3 基于蒙特卡洛模拟的供应链金融质物价格风险的度量

(1) 短期动态价格风险测度

为了避免多期预测带来的不精确性，我们采用滚动时间窗的风险预测方法测度短期动态价格风险，即首先利用样本数据(t=1,2,…,1455)，预测第1456个交易日的风险值，随后保持样本量不变(T=1455)，将样本向后平移1个交易日，进而计算出短期动态价格风险值。

假设两种质物的收益率分别为X1和X2，其边际分布分别用F(x1)和F(x2)表示。

首先，确定所要计算的价格风险VaR和CVaR的置信水平，本文选取90%、95%和99%。

其次，产生随机数。根据选择出的描述两种质物收益率相关结构的最优Copula函数以及Copula相关参数，通过蒙特卡洛模拟产生服从[0,1]均匀分布的二维随机样本u1和u2。

然后，模拟收益率。通过各边际分布函数F(x1)和F(x2)，经过逆概率变化得到相应的收益率x1=F(U1)和x2=F(u2)。

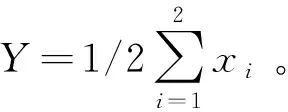
接着，多次模拟，逐渐逼真。重复上述过程3000次，模拟得到各样本质物第1456个交易日价格风险价值的3000种可能情景值，由此可得到价格收益率的经验分布。

最后，计算VaR和CVaR。将模拟得到的3000个收益率按照从小到大的顺序进行排序，排序后的收益率序列中下方α分位数，也就是第3000×(1-α)个模拟值为该置信水平下的质物组合风险值VaR。本文按照CVaR的定义，用大于VaR的全部值的平均值来估算价格风险CVaR值。

为了将传统方法测度的质物组合的价格风险与基于Copula函数测度的风险进行对比，本文利用蒙特卡洛模拟法测度了单一质物的短期动态价格风险值。与上述步骤类似，不同的是在第二步产生随机数过程中，是利用Matlab生成服从[0,1]均匀分布的随机数u，通过边际分布函数F(x)，经过逆概率变换x=F-1(u)，得到样本质物收益率。

(2) 长期价格风险测度模型

在供应链金融业务中，存货等质物具有流动性较弱、清算期较长、存在质押期限等特征，这无疑会使质物价格风险的持有期加长，因此有必要对供应链金融质物价格的长期风险进行预测。本文借鉴我国学者何娟等[15]的研究，采用时间平方根法则来预测供应链金融质物组合的长期价格风险，同时采用单日VaR的均值来代替单日VaR值，以此来解决单日风险预测的高估或低估。在具体的实践中，质押期往往不会超过1年，据此本文分别选择1天、2周、1个月、3个月、6个月、9个月以及12个月共7个风险窗口作为长期价格风险窗口期。

在计算出255个滚动的短期动态价格风险VaR和CVaR后，我们借助时间平方根法则计算质物的长期价格风险。长期风险预测的具体解析式(以VaR为例，CVaR的计算与VaR类似)如下：

(7)

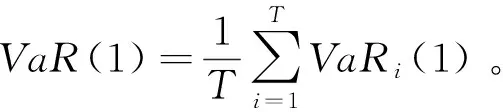
关于传统测度长期价格风险的方法(无风险分散)即为组合内各质物价格风险的VaR值的简单加权平均。二元质物组合长期价格风险的计算如下:

VaR(T)=ω1VaR1(T)+ω2VaR2(T)

(8)

其中ω1、ω2分别为单一质物的权重，本文进行加权平均，均为1/2。

为了更好地把握模型的可靠性，本文采用Kupiec提出的基于失败频率的返回检验法对各种模型下的供应链金融质物组合价格风险值的有效性进行检验。本文选择检验天数为255个交易日，即以样本内的第1个交易日至第1455个交易日的日对数收益率数据为时间窗口，通过每次移动一个时间窗口预测第1456至1710个交易日的短期动态风险值。

2Ln[(1-P*)T-N(P*)N]～χ2(1)

(9)

3 实证分析

3.1 样本选取与统计性特征分析

在供应链金融业务的具体实践操作中，一般会选择物权清晰，性质稳定，易于仓管、运输与结算，流动性强、以及市场前景良好且价格公开透明的产品作为质押物。基于以上原则，本文拟选取长江有色市场1#白银、A00铝、1#铜三种质物作为样本质物。本文选择三种质物的日现货交易均价作为样本数据，数据均源自万德数据库。本文选择2010年1月1日至2017年1月18日期间交易日的数据作为样本数据，鉴于个别数据缺失和各样本的数据区间保持一致，在此只对三种样本质物均存在交易情况下进行统计，并未做任何插值处理，样本区间共1710组数据，其中选择2010年1月1日至2015年12月31日区间的日交易价格数据用于估计模型参数，共1455组数据，2016年1月1日至2017年1月18日区间255组样本数据用于评价模型效果。

为消除价格波动对于价格水平的依赖关系，本文通过对三种质物价格的原始数据进行对数差分，以此获得各质物价格t时刻的对数日收益率数据：Rt=Ln(Pt)-Ln(Pt-1)，其中Pt为该质物在t时刻的价格。白银、铝和铜的对数日收益率序列如图1所示。

图1可以看出三种质物的收益率波动表现出较为显著的集聚效应，具有一般金融资产收益率波动的特征。同时下表列出了三种质物对数收益率的描述性统计分析结果。

图1 三种质物日对数收益率变化趋势图

表1 单一质物收益率统计性描述表

由表1可知，白银、铝和铜三种质物的日对数收益率偏度值均小于0，表明三种质物的收益率序列均为左偏分布，同时其峰度远大于标准正态分布的峰度，说明该收益率序列是典型的高厚尾分布，具有显著的“尖峰厚尾”特征。据此，可初步判断三种质物的对数收益率序列不服从正态分布。为了更清楚地了解三种质物日对数收益率序列分布，本文采用K-S检验和J-B检验来判断其是否服从正态分布，结果如表2所示。由下表可以看出三种质物均拒绝了原假设，表明白银、铜和铝三种质物的收益率序列均显著不服从正态分布，进一步说明三种质物对数收益率序列服从某种“高峰厚尾”分布。

表2 供应链金融三种单一质物收益率分布的正态性检验结果

综上所述，白银、铜和铝三种质物的对数收益率序列均表现出显著的非正态分布，具有“尖峰厚尾”特征，因此可采用金融市场风险测度方法，即建立Copula-CVaR模型来测度供应链金融质物组合的价格集成风险。

3.2 边际分布的确定

上述分析可知，白银、铝和铜三种样本质物的日对数收益率服从某种尖峰厚尾分布，而常见分布中很难找到这种类型分布，因此本文选用非参法中的核密度估计法来对三种质物的收益率边际分布进行估计。图2中的灰色曲线分别是利用Gaussian核函数求出质物白银、铝和铜的核密度曲线。从图中结果可看出，核密度估计曲线较好地拟合了三种质物日对数收益率，也就是说白银、铝和铜三种质物的核密度估计能够较好地拟合其边际分布。

图2 供应链金融三种单一质物的频率直方图与核密度估计图

为了进一步确定三种质物的边际分布，本文调用Matlab中的ecdf函数求得样本经验分布函数，如下图中的灰色曲线所示，图中的黑色曲线是采用上一步的Gaussian核函数估计出的分布函数曲线。不难发现，三种质物的经验分布函数图与核密度估计的分布函数图几乎是重合的，基于此，我们可认为利用核密度拟合边缘分布与利用经验分布函数拟合边缘分布的结果是一致的，即利用Gaussian核函数估计供应链金融单一质物的边际分布是合理准确的。

图3 供应链金融三种单一质物的经验分布函数图与核分布估计函数图

3.3 基于多元Copula的质物组合联合分布的确定

(1)三种质物价格风险的边际分布拟合检验

表3中的K-S统计量及其概率值均表明，在1%的显著性水平下供应链金融三种单一质物白银、铝和铜的边际分布均服从(0,1)均匀分布，满足利用Copula模型度量质物组合中质物价格间相关结构的要求。以此为基础，下文可以进一步对Copula模型参数进行估计并选取出最优Copula模型，以此获得质物组合的联合分布。

表3 供应链金融三种单一质物的边际分布拟合K-S检验

(2)Copula模型参数估计及最优Copula模型选择

五种Copula模型的参数估计结果如表4和表5所示。

表4 供应链金融二元质物组合正态Copula与t-Copula相关结构参数表

表5 供应链金融二元质物组合阿基米德Copula函数参数估计值

根据前文模型构建，在计算出五种Copula模型参数之后，本文通过计算二元质物组合的理论Copula函数与经验Copula函数之间的平方欧式距离来检验拟合优度，检验结果如表6所示。

表6 供应链金融二元质物组合五种Copula模型平方欧式距离

从表6我们不难看出，在白银和铝、白银和铜以及铝和铜三组质物组合中，t-Copula模型的平方欧式距离最小，分别为0.0278、0.0324、0.0273；而Clayton-Copula模型的平方欧式距离最大，分别达到0.1431、0.1739、0.3303。由此，我们可以认为t-Copula模型是刻画质物组合中质物间相依关系的最优选择，表明白银和铝、白银和铜、铝和铜三组质物组合不仅具有对称的尾部，而且尾部较厚。在选择出最优Copula函数后，结合单一质物边际分布，我们可以求出供应链金融二元质物组合的联合分布。

3.4 基于蒙特卡洛模拟法的供应链金融质物价格风险VaR和CVaR测度

(1)单一样本质物价格风险VaR和CVaR测度

1)单一质物短期动态价格风险VaR和CVaR测度及失效率检验

依据构建的模型，本文采用滚动时间窗口的风险预测方法，运用蒙特卡洛模拟法来测度90%、95%和99%三种置信水平下白银、铝和铜三种质物第1456个交易日至第1710个交易日的短期动态价格风险值VaR和CVaR，共255个。由于篇幅原因，具体VaR和CVaR值在此不列出。之后需要运用Kupiec的失败频率检验法对各个模型的有效性进行检验。本文选择考察天数为255个交易日，根据失败频率检验原理，可计算出样本数据为255时失败频率检验接受原假设的区间和比例，如表7所示。

表7 失败频率检验接受的区间和比例

依据表7和单一质物短期动态风险值，下表汇总出当考察天数为255天时，供应链金融三种单一质物在不同置信水平下价格风险VaR和CVaR模型的失败次数。

表8 T=255时供应链金融单一质物价格风险VaR和CVaR模型的失败次数

基于表8结果，从风险测度模型的有效性来看，VaR和CVaR值通过失败频率检验的天数均在失败频率检验的接受区间内，这说明了VaR和CVaR均可衡量三种单一质物的价格风险。但是具体而言，CVaR的失败次数小于VaR的失败次数，这主要是因为CVaR模型考虑到极端事件的发生，因此质物价格损失大于其CVaR值的概率较小，模型对极端事件发生预测成功的可能性就越大。基于此，从考虑极端价格波动的角度出发，CVaR方法比VaR方法更可靠。

2)单一质物长期价格风险VaR和CVaR测度

根据短期价格风险测度结果，采用时间平方根法则对三种单一质物的长期价格风险进行预测，结果如表9所示。

表9 不同风险期限下三种单一质物长期价格风险值

表9我们可以得出以下结论：

第一，根据VaR和CVaR的定义，在接下来一天，白银、铝和铜的日对数收益率，有99%的把握可以认为其损失不会超过0.04978、0.01908和0.03305，如果损失超过了这些值，那么有99%把握可以确定三种质物收益率的损失期望值即平均损失会达到0.06831、0.02302和0.04209。同理，可对其他置信度和风险持有期下的三种质物的价格风险进行分析，分析结论可以为商业银行在供应链金融业务价格风险管理方面提供一些直观而翔实的资料，有助于商业银行作出正确抉择。

第二，从上表可以看出，三种质物白银、铝和铜的价格风险VaR和CVaR值随着风险持有期的增加而增大，符合金融风险相关理论，风险持有期越长，白银、铝和铜的价格波动的不确定性就越大，表现在风险价值上即VaR和CVaR值变大。

第三，在每一种置信水平下，白银的价格风险值VaR(或CVaR)最大，其次是铜，风险最小的是铝。该结果与直观观测结果是一致的，具体而言，一方面从前文的三种质物日对数收益率变化趋势图不难看出，相较于铝，白银和铜收益率的波动较大，产生的风险也就随之较大。另一方面从统计特征结果来看，白银、铝和铜确实呈现出显著“尖峰厚尾”、波动集聚性等特征，其中，白银的左尾厚尾特征特别明显，更易产生极端损失。此外，白银收益率的均值要大于铝和铜的收益率，可以说白银相对于铝和铜而言收益大，风险也大。总而言之，商业银行在构建质物组合时，可以加大铝的持仓比例，减少白银的持仓比重。

(2) 二元质物组合价格风险VaR和CVaR测度

1)二元质物组合短期动态价格风险VaR和CVaR测度及失效率检验

从表6可知t-Copula函数能够最优刻画两种质物间的相依关系，其次是正态Copula，因此很大程度上我们可以认为正态Copula和t-Copula能够较好地拟合三种质物构成的二元质物组合的联合分布，基于此，我们选择正态Copula和t-Copula来拟合质物组合的联合分布。按照上一节构建的二元质物组合短期动态价格风险测度模型，通过每次移动一个时间窗口预测出第1456至1710个交易日的短期动态风险值，共255个。由于篇幅原因，具体VaR和CVaR值在此不列出。同理，计算出短期风险值后需要对各个模型的有效性进行检验，下表汇总出当考察天数为255天时，基于正态Copula和t-Copula模型下供应链金融二元质物组合在不同置信水平下价格风险VaR和CVaR模型的失败次数。

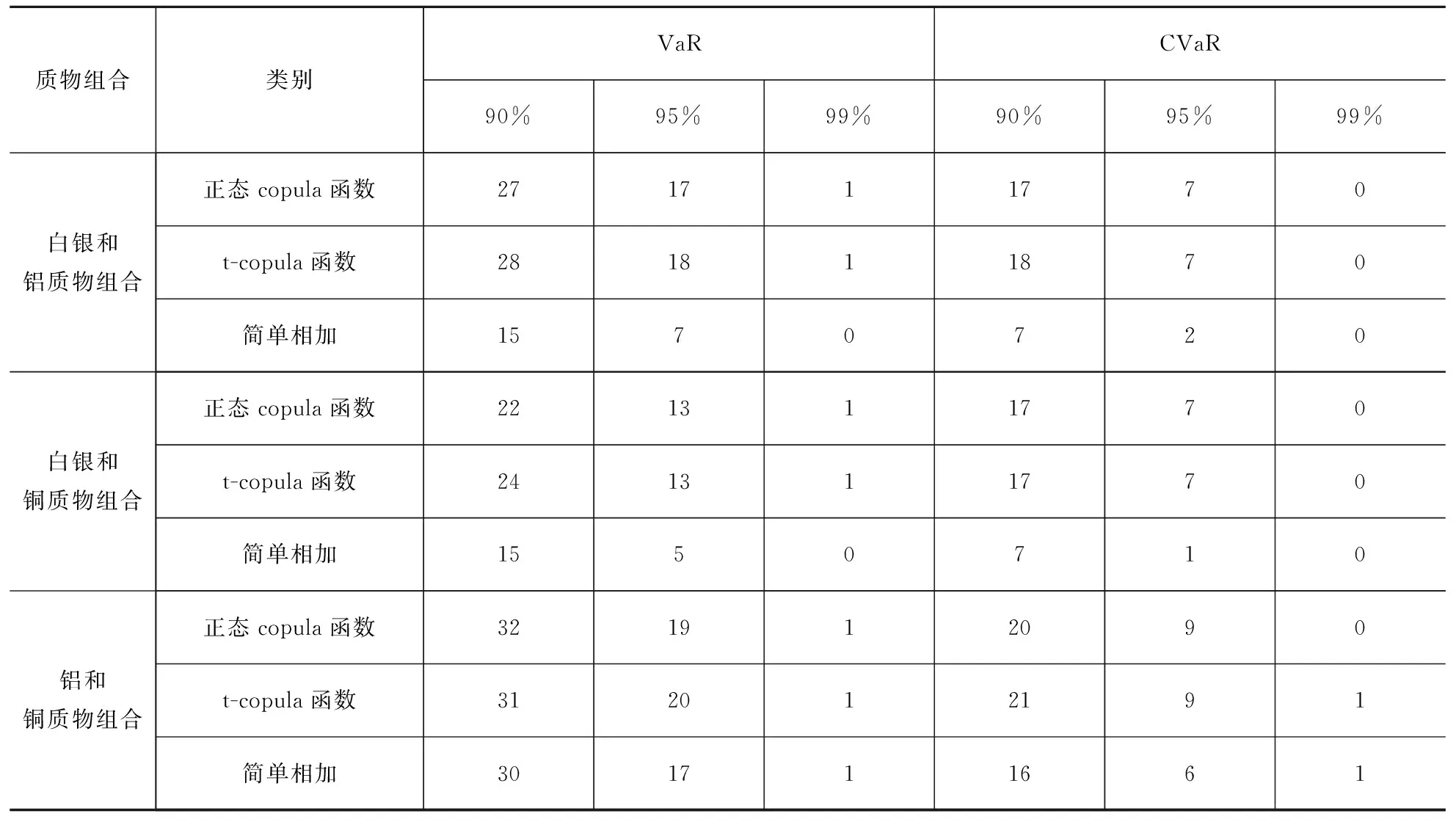
表10 T=255时供应链金融二元质物组合价格风险VaR和CVaR模型的失败次数

从表10可以看出：从模型的有效性来看，一方面无论何种置信水平下，基于正态Copula模型和t-copula模型下白银和铝、白银和铜、铝和铜三种质物组合的价格风险VaR和CVaR模型的失败次数都在失败频率法接受区间内，而基于传统的集成风险方法测度的质物组合的价格风险结果并没有完全通过回顾测试。因此正态Copula函数和t-Copula函数能够有效地刻画二元质物组合中质物价格风险因子间的相依关系，并且基于Copula函数构建的风险测度模型可以有效地测度质物组合价格风险，而传统的集成风险测度方法并不能有效地测度供应链金融质物组合价格集成风险。另一方面，与单一质物价格风险回顾测试结果相似，无论是不同类型的质物组合，还是不同模型、不同置信水平，CVaR的失败天数都小于VaR的失败天数。因此结合以上两点，可认为CVaR比VaR能够更好地、全面地刻画供应链金融质物组合损益分布。

2)二元质物组合长期价格风险VaR和CVaR测度

本小节在前文基础上运用上述四种模型来测度供应链金融质物组合的长期价格风险VaR和CVaR，同时便于与传统风险测度方法(不考虑风险间的相关性)进行比较分析，我们还给出了二元质物组合价格风险传统方法(将两种单一质物价格风险进行简单相加)的测度结果，结果如表11所示。

表11 供应链金融二元质物组合长期价格风险测度结果

续表11

表11给出了风险持有期分别为1个交易日、2周、1个月、3个月、6个月、9个月和12个月时供应链金融二元质物组合的价格风险测度结果，从上表我们可以得出以下结论：

第一，不同的风险持有期内，三组质物组合的价格风险不同，但具有逐渐增大的趋势，因此商业银行在对供应链金融业务质物组合价格风险进行管理时要特别关注长期风险。

第二，在同一风险持有期和置信度下，三组供应链金融质物组合中，白银和铜组合的风险值VaR和CVaR最大，其次是白银和铝质物组合，而铝和铜质物组合的风险值最小。这与单一质物价格风险大小排序相一致，前文中我们可知单一质物白银的价格风险大于质物铜，质物铝的价格风险最小，因此质物白银和铜相组合，其风险最大的可能性较高，相对而言，铝和铜的风险都比较小，其组合风险也就较小。

第三，在同一置信度下，质物组合的CVaR值大于VaR值，但是不同质物组合之间的这种差异比较大。通过对上表数据进行整理，发现在同一置信水平、相同的风险持有期下CVaR与VaR之间的差异性大小排序基本上是：铝和铜这一质物组合的CVaR与VaR的之间差异性最小，其次是白银和铝这一质物组合，而白银和铜质物组合的CVaR与VaR的差异性最大。这主要是因为白银和铜质物组合的波动性大，风险值也较大，因此CVaR与VaR之间存在差异性的概率就会越大。同时我们也不难发现随着置信水平的增加，CVaR与VaR之间的差异逐渐增大，99%置信水平下CVaR与VaR之间的差异最大。

第四，基于正态Copula模型测度的供应链金融质物组合价格风险价值VaR和CVaR高于t-Copula模型下测得的结果。特别是白银和铜质物组合以及铝和铜质物组合中，正态Copula与t-Copula模型下测度的价格风险差异较大，而白银和铝质物组合中两种Copula模型的测度结果相差不大。因此，对比最优的t-Copula函数，正态Copula模型不管是在何种置信水平下都会高估供应链金融质物组合的价格集成风险。

第五，采用正态Copula连接函数和t-Copula连接函数所计算的供应链金融质物组合的价格集成风险VaR或CVaR小于将供应链金融单一质物价格风险因子的VaR或CVaR简单相加得到的质物组合的价格集成风险，因此不考虑不同质物价格风险因子之间的实际相关性往往会高估质物组合的价格集成风险。对于商业银行而言，风险的高估将会降低资金的使用效率，并且限制了供应链金融业务的发展。

4 结论

本文通过构建Copula-CVaR模型对供应链金融白银、铝和铜三种质物两两构成的质物组合的价格风险进行测度研究，主要得到以下结论：从单一质物价格波动性来看，三种单一质物的收益率均存在非正态分布和“尖峰厚尾”特征，具有一般金融资产收益率分布的特点，可以用VaR和CVaR方法来度量供应链金融质物的价格风险。从价格风险模型测度的有效性来看，第一，无论是单一质物还是质物组合的价格风险测度，CVaR模型优于VaR。一方面CVaR模型和VaR模型的失败天数都在回顾测试的可接受区间内，表明两种方法均可用来测度供应链金融单一质物和质物组合的价格风险，但是在可接受区间中，CVaR的失败天数明显少于VaR的失败天数。另一方面，K-S检验和J-B检验均表明质物组合的收益率序列不服从正态分布，而存在“尖峰厚尾”的分布特征，同时能够最优刻画质物组合收益率间的相依结构的t-Copula也表明质物组合收益率存在厚尾现象。综上分析，同时结合VaR和CVaR的定义，可认为CVaR模型比VaR能够更好地刻画供应链金融质物组合的价格风险。第二，t-Copula比正态Copula更能准确刻画供应链金融质物组合间的相关结构。供应链金融质物组合收益率分布具有对称的尾部，而且尾部较厚，由于尾部相依程度的提高，组合中各质物价格极端变化事件得以抵消的概率也会随之提高，因此基于正态Copula模型下的风险测度结果将会高估质物组合的价格风险，不利于商业银行的资金配置。而同时，基于传统集成风险测度方法计算的风险值VaR和CVaR在90%和95%置信水平下并没有通过回顾测试。因此基于t-Copula构建的风险测度模型最有效。从风险测度结果来看，质物间的价格波动存在一定的非线性相关性，因此传统集成风险测度方法(简单相加或认为是线性相关)计算的价格风险值要大于考虑了质物收益率间相关关系情况下的风险值，可认为前者高估了质物组合的价格风险。从长短期风险值对比结果来看，随着风险期限的增加，质物组合的价格风险值随之增大。而对于商业银行而言，质押期的存在以及存货较弱的流动性均表明商业银行在开展供应链金融业务过程中更应关注长期价格风险，以往研究中的短期风险测度往往会低估商业银行所面临的价格风险，不利于商业银行资金信贷的优化配置。