考虑回收-补偿约束的卫星城镇生活垃圾中转站选址研究

李海君, 张耀文, 杨月巧

(1.防灾科技学院 应急管理学院，河北 三河 065201; 2.防灾科技学院 生态环境学院，河北 三河 065201)

0 引言

我国城镇化过程发展迅速[1]，而中小城镇，尤其大都市周边卫星城镇，固废处理需求与收运管理系统滞后处理能力间矛盾突出。目前该类城镇多采用一次转运或直接配送收运方式，设施配置基本未进行经济、环境或社会效应优化，系统运营耗资大，固废回收率低，且污水、废气等负效应显著。其中，选址、建设约束相对灵活的中转设施，成为城镇生活固废资源、经济、无害化处理的关键因素。

为实现收运系统的合理优化配置，国内外学者已采用定量或定性方法进行中转站选址研究。1996年，Thierry Kulcar[2]在已知某街区中转站备选点收运路线情况下，首次采用混合整数模型以最小转运成本为目标进行转运设施优化选址，而后Noche[3]、何波[4]等学者以最优经济效益为目标进行中转站选址或二次优化；Ghose[5]、Benjamin[6]、贾学斌[7]、陈勇[8]等则通过VRP或仿真模型结合分配方案、转运路径进行了中转站选址研究。近年来，国内部分学者亦对中转站运营过程中负面环境效应对其选址影响进行了相应研究，Chang[9]、李安宇[10]、王海燕[11]、周方圆[12]等综合负效应或二次污染风险控制建立多目标优化选址模型。陈佛保[13]则从市场化角度基于邻避设施负面支付意愿，量化分析了垃圾中转设施的邻避效应。此外，亦有学者采用模糊理论[14]、AHP[15]、生命周期[16]、指标满意度[17]等综合决策方法针对中转站选址进行定性研究。其中，仅考虑收运时间最短或费用最小的优化模型对环境约束因素考虑不够全面、充分，而综合了负效应控制的多目标决策优化模型运算求解属N-P Hard问题，专业性较强。另外，定性模型主观性较强，即使部分结合优化过程，仍不便进行决策结果量化分析。

本文结合卫星城镇垃圾收运系统实际现状与现有规范约束，综合考虑固废产生特征与城镇背景资料确定待选点，首先应用改进LSCP模型，确定能够一次全部覆盖所有收集点的中转站备选点组合；在此基础上，综合最小固定投入、负效应补偿和转运费用与风险，同时兼顾最大回收效率等因素建立多目标优化模型，确定中转站位置、规模与服务分配方案。通过本文优化模型方法构建及实证研究，以期为卫星城镇中转设施选址提供合理实用模型方法。

1 选址优化影响因素

据已有文献综述，城市垃圾中转站选址影响指标可归纳为固定与运营成本、负效应控制、固废资源化或回收程度，以及规划适应性等方面。然而，卫星城镇固废收运系统基本未经系统优化，配置与管理粗放，且系统无害化与资源化程度较低，故其转运设施优化选址影响因素相对复杂。本次研究认为，该类垃圾收运系统应以满足收运基本功能并兼顾负效应控制为前提，确定尽可能少的备选设施；以此为基础，进而综合考虑系统建设成本、转运成本、最大回收效率与负效应控制等多个目标确定最终中转站组合。

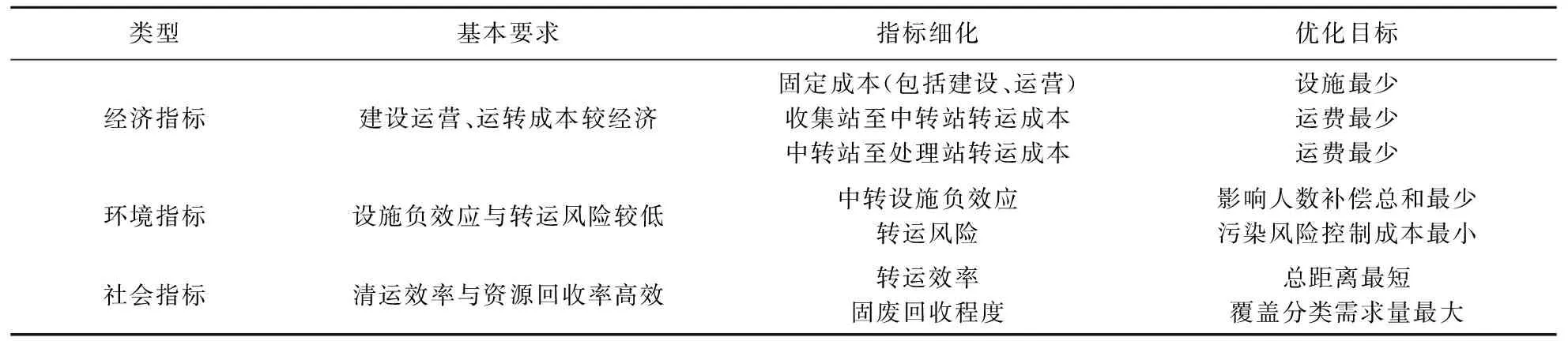
表1 选址影响因素与优化目标

综上，选址因素与优化目标应着重考虑经济、环境与社会等主要因素，其中，经济与环境指标既应控制中转设施个数与规模，亦要做好系统配置优化以控制转运成本与风险；同时，固废资源化程度与转运效率、邻避问题合理处置等社会性指标则多为政府公共事务管理水平重要体现。

2 中转站层级选址模型

2.1 问题描述与假设

本次研究拟通过试算方法，逐次增大收运距离，于待选点中结合设施容量、转运距离确定垃圾中转站备选点组合与规模；在此基础上，通过控制中转固定投入、转运成本与风险、设施负效应以及回收效率，确定中转站最优组合与收运方案。为简化模型，作如下假设 ：

(1)收集站点不考虑收集费用，位置确定，收集顺序无差异且固废日产生量不变；

(2)运费、转运风险与转运距离呈线性相关，并考虑中转站至处理站转运成本与风险；

(3)处理站规划、建设约束严格，需进行严格环境影响评价，假定处理设施已确定；

(4)中转设施负效应与规模相关，压缩、回收功能满足要求，暂不考虑处理站负效应；

(5)转运周期内各级固废暂存量不超设施规模容量，并假设备选点转运周期为一日。

2.2 优化模型

优化过程可分中转站备选点优化与中转站选址优化两阶段，其中前者需用尽可能少设施覆盖所有需求点，后一阶段则需结合多目标选址模型进行计算分析。

(1)中转站备选点优化模型

设I为收集点集合，J为待选点集合，则中转站备选点选址优化模型可表述如下：

(1)

(6)

其中，yj表征是否选中待选点j作为中转备选点，是取值1，否则为0；Gi代表收集点i垃圾日产生量(kg·d-1)；xij定义为0-1变量，表征i处固废是否运往待选点j；dij为收集点i与待选点j之间的实际距离(m)。此外，δj定义为中转设施处理能力(kg·d-1)，Df表示转运距离上限(m)，两参数均参照《城市环境卫生设施规划规范(GB50337-2003)》[18](下称“《规范》”)递增设定；Nf为待选点个数，限制备选集合规模。目标函数1表征从Nf个待选设施中确定一次全部覆盖所有收集点的最优备选组合；约束(2)保证每个收集点固废单日均能被清运，且仅被清运一次；约束(3)确保设施j处理能力满足所覆盖所有收集点的固废产生需求；约束(4)要求运输距离不得超过规范规定约束值；约束(5)限定既定待选集合数量规模；约束(6)定义既定需求与待选集合均为0-1变量。

(2)中转站选址优化模型

在确定最优备选组合的基础上，假定已有处理站设施有足够处理能力且位置固定前提下，本阶段需进一步考虑表1中经济、环境与社会等指标确定最终中转站位置、规模。综合成本、负效应与回收效率等量化指标，以及中转站至处理站转运成本与风险控制成本，以I为收集点集合，中转站备选点优化结果Je为备选点集合，将优化模型确定如下：

(1)

(8)

目标函数1由储运-回收系统最小运营、风险控制与补偿成本，以及最大固废回收量两部分构成，其中分子表征建设与收运成本之和，依次由收运转运成本(含风险控制费用)、日均固定投资、补偿费用三部分构成；分母则定义为最大回收量；约束2保证每个收集点固废单日均能被清运，且仅被清运一次；约束(3)式要求固废仅能运送至选中中转设施；约束(4)、(5)要求中转站收容能力与收运距离不超过《规范》限定最大值；约束7限定备选集合设施个数，而约束8定义收集点与备选集合均为0-1变量。

2.3 模型求解

本次研究经DRG格式底图文件数字化，结合实地调查，应用GIS空间分析功能获取基础决策数据。利用lingo优化软件进行两阶段优化，依次确定中转站备选点与中转站位置、规模与服务分配方案，具体求解步骤如下：

(1)建立地形、气象、道路、城市用地、人口以及现有基础设施等图层，叠置分析确定选择较适宜的中转站待选点集合；

(2)通过网络分析建立收集点与中转站待选点与备选点之间O_D矩阵；

(3)根据城市用地类型考虑固废产生特征，确定收集点集合，核实需求量与回收率；

(4)应用lingo软件编程，采用中转站备选点优化模型确定备选点位置与规模；

(5)在此基础上，采用中转站选址优化模型，编程确定中转站位置、规模，并确定最优组合中各设施服务分配方案。

3 实例分析

3.1 研究区概况

研究区为廊坊北部经济开发区，地处京冀交界，总面积约105平方千米，人口81.81万人，其辖区中部综合服务区为主要生活固废产生源区。区内现建有处理能力为800t·d-1垃圾处理站1座，以及转运能力200t·d-1中型中转站一处。考虑已有资源利用效率，应用本文中转站备选点与选址优化模型方法对其收运系统进行二次优化。

图1 研究区收集点、待选设施分布

根据当地社会、经济、交通以及固废产生情况，结合收集站与中转站选址相关规定、规范，区内确定收集点154处，中转站待选点51处。另据实地调查与规范资料查阅结果确定表2参数：

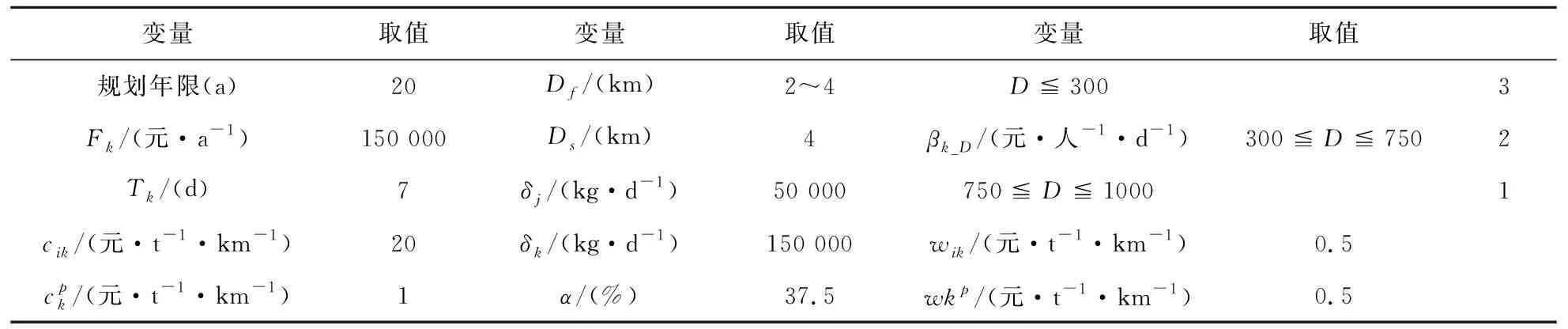
表2 研究区垃圾收运系统参数取值

3.2 计算结果与分析

结合概化收集点与设施待选点，获取收集点与中转站待选点及待选点至至处理站O_D矩阵，采用表2模型参数，经优化可得以下结果：

(1)据《规范》，小型机动车收运服务半径一般为2.0～4.0km为宜，故本次研究采用试算法，设定中转站备选点模型距离。将2km作为试算下限，以“100m”为步长，应用中转站备选点优化模型计算，可知：收运距离2.0～2.2km、3.2～4.0km时，分别可得全局最优解，计算确定备选点26与23；收运距离为2.3～2.7km、2.8～3.1km时，可依次确定可行解为25与24。而后，分别以2.0km、2.2km、2.7km、3.1km、3.2km、4.0km作为距离节点，以最小转运成本为目标采用P-中值模型，依次选定对应设施数进一步分析，计算见表3。综合表1细化指标，为控制环境负效应与固定投入成本，并综合附加距离、选定设施数约束的P-中值模型计算结果进行筛选。经求解、分析，本阶段模型模型迭代24 882次，即确定最少备选设施数目23个，选中备选设施D1、D3、D4、D6、D7、D8、D9、D11、D12、D15、D18、D19、D20、D25、D29、D37、D38、D39、D42、D43、D47、D48、D50，且确定收运距离以3.2km～4.0km为宜。

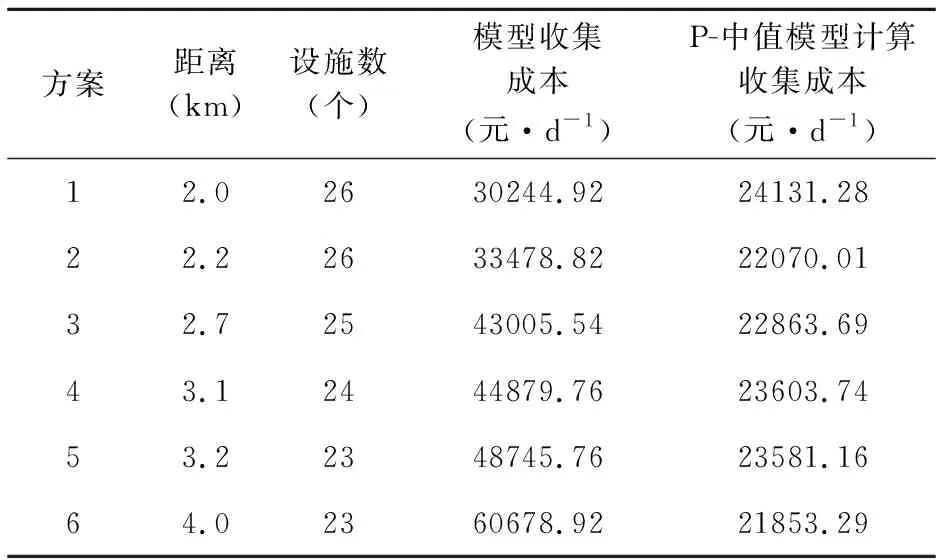
表3 备选点优化结果

(2)本次研究将中转站对周边居民点负效应，以不同等级距离做缓冲核算影响人数，并分别核算补偿(见表2)，另暂不考虑新增处理设施前提下，本次将中转站至处理设施转运费用与风险防控附加费用视为中转站“固有成本”。此外，为保证模型求解可行性与求解效率，将中转站选址优化模型约束距离设置为《规范》规定最大限制，即将Ds参数设为4000m。由此，经模型优化计算，可得多个非劣最优解，本次研究应用生成法从非劣解集中确定最终解。据解集决策参数(见表4)，结合不同设施组合规模下的目标函数值，进而兼顾最小环境负效应与转运成本和风险，最终确定将选中8个设施的解2作为最优解。其中，解2共重复926 280次，得全局最优解2.196866×10-4，最大总回收覆盖规模为9.164458×105t，补偿成本为135 821元，转运成本为62 222.20元，选中设施8个，依次为D1、D4、D7、D11、D12、D25、D39和D48，各设施服务收集点、收集量与回收量见表5。

表4 中转站选址优化模型最优解集

(3)将研究区决策基础数据应用文献[19]技术方法，在未约束收运距离的前提下，模型迭代353 961次，确定中转站备选点最少设施个数为23个，依次为D1、D2、D8、D11、D13、D15、D18、D22、D23、D26、D30、D31、D33、D35、D36、D38、D39、D40、D43、D45、D49、D50、D51。在此基础上，进而应用其垃圾中转站优化选址模型，迭代532次即确定中转站12个，依次为D2、D11、D15、D18、D22、D31、D33、D35、D38、D43、D49、D51，收运费用共计36 844.01元，但按本次研究标准，计算中转站组合的负效应补偿成本总计456 771.55元。另为保证模型可比性，给定设施数8，该选址模型重复83 011次，确定中转站设施D11、D15、D22、D33、D35、D38、D43、D51，收运费用41 256.41元，负效应补偿费用413 383元。

表5 中转站优化结果

(4)中转站备选点确定过程中，本文模型因依据《规范》设定转运距离上限，进而计算效率相对参引文献模型略高；而在中转站设施选址过程中，参引文献应用最小成本进行选址优化，所确定设施均分布在城镇内部高人口密度区，而本文模型方法兼顾负效应补偿与固废最大覆盖回收，计算结果多分布于人口密度较小的城镇非中心区，且求解效率低于参引文献。在同等设施规模满足固废清运需求前提下，按本次研究标准，本文模型计算转运成本较参考文献计算结果高50.82%，但补偿成本却少67.14%，日均总成本少56.03%。因而，本文模型方法较参引文献模型计算效率较低，但优化确定的中转站组合结果更为经济、合理。

4 结论

本文针对卫星城镇生活固废垃圾收运现状与需求，应用规范规定距离改进LSCP模型，经试算于3.2km服务半径下即可确定中转站备选点23个；据此结果，适当放宽收运距离，综合考虑运营、转运成本与风险、负效应控制与回收效率，应用中转站优化选址模型确定中转站设施8个，并给出服务分配方案。结合实例分析，验证了本文模型、方法的可行性。相比文献[19]，本文模型方法求解效率虽低，但考虑因素更为综合、实际，确定设施组合相对经济、合理。