损伤分析的精确增量迭代算法

赵冰，宋文浩，陈健，彭晖，彭旭龙

(长沙理工大学 土木工程学院，湖南 长沙 410004)

损伤非线性分析已应用于众多领域，如：材料疲劳寿命的预测、构件裂纹的萌生与扩展及岩土强度的分析等。对于损伤力学，其结构应力依赖于变形历史，全量理论已不再适用。必须采用增量理论，跟踪结构的平衡路径。因此，增量平衡方程在非线性分析中，得到了广泛的应用。唐雪松[1−2]等人采用损伤力学-有限元法，研究了加载次序对疲劳寿命的影响作用，并对标准疲劳试验构件进行了疲劳寿命预测。张杰毅[3]等人采用损伤力学-有限元法，预估了球轴承的接触疲劳寿命。李聪成[4]等人采用损伤力学有限元法，分析了蠕变疲劳交互作用下，影响裂纹萌生寿命的因素。张我华[5]等人将损伤力学引入岩石类介质的非线性本构模型，分别建立了脆性动力和弹黏塑性动力的损伤模型，并编制相应的有限元程序，分析岩石的动力学行为。损伤非线性分析已运用到医学领域。Taylor[6]等人采用损伤力学-有限元法，模拟了人体骨骼在人造环境内的疲劳行为，应用于人体脑骨骼样本的疲劳失效次数、弹性模量的退化及骨骼内永久应变的累积状况。考虑这些传统损伤有限元分析中的增量迭代算法，会产生迭代无法消除的漂移误差。作者拟提出一种全新的增量迭代方法：正割刚度-附加荷载法(Secant stiffness– additional load method,简称为 SSALM)，以校正传统增量迭代法的全部漂移误差，寻求其真实的结构响应，以提高算法的稳定性。

1 传统损伤算法中漂移误差的成因

损伤非线性有限元格式可简单分为两类：

1) 第一类是利用力的平衡条件(内力与外力平衡)或虚功原理得到的全量形式[7]：

式中：KS(u)为结构在某种状态(λ,u)下的正割刚度矩阵；u为结构位移矢量；B为应变矩阵；σ为全量应力张量；Ωe为单元体积；G为组装矩阵。

外力由荷载因子λ与基准荷载矢量f的乘积形式表示。当结构的外力与内力处于非平衡状态时，则体系内存在残余力矢量r为：

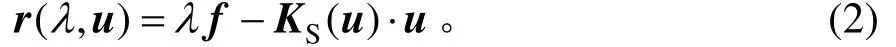
全量应力张量σ可由损伤本构表达式为[8]：

式中：ε为全量应变张量；CD为损伤本构张量。

将式(3)代入式(1)，全量平衡方程为：

2) 第二类为增量平衡方程，其有限元基本式[9]为：

式中：Δσ为增量应力张量；Δu为增量位移矢量；Δλ为增量荷载因子；KT(u)为切线刚度矩阵。

在实际应用过程中，常采用增量的伤本构[10]：

对式(6)进行线性化处理[11]，可得：

将式(6)和(9)称为传统增量迭代法，而式(9)是传统增量平衡方程。该方法已应用于许多领域，如：疲劳寿命预测[1−3]和高阶梯度损伤理论[12]等。对比式(5)，(9)可以看出，式(9)中的传统方法是采用KS(u)代替了式(5)的KT(u)。然而，切线刚度矩阵[13]由式(2)导出：

单纯地采用增量法，必然引起解的漂移[13]。如果没有模型误差，这种解的漂移通常是通过在增量步内设置迭代来校正的[13]。因为传统增量迭代法忽略掉了。所以，导致增量平衡方程所表征的平衡路径失真，而引起漂移误差，并且不能通过迭代技术消除。采用KT(u)表达的增量迭代算法，在峰值点附近，常常存在刚度矩阵病态化、奇异化及收敛性差[14]等问题，其稳定性在很大程度上取决于KT(u)的条件数。

2 SSALM 法

对式(2)进行全微分展开，可得：

将式(10)代入式(11)，可得：

对于损伤力学，正割刚度矩阵KS(u)的表达式为：

将式(13)代入式(12)，可得：

式(14)可简写为：

式中：i为当前平衡状态；i-1 为上一个平衡状态。

其中，λi>λi−1。利用式(17)减去式(18)，则可得增量平衡方程为：

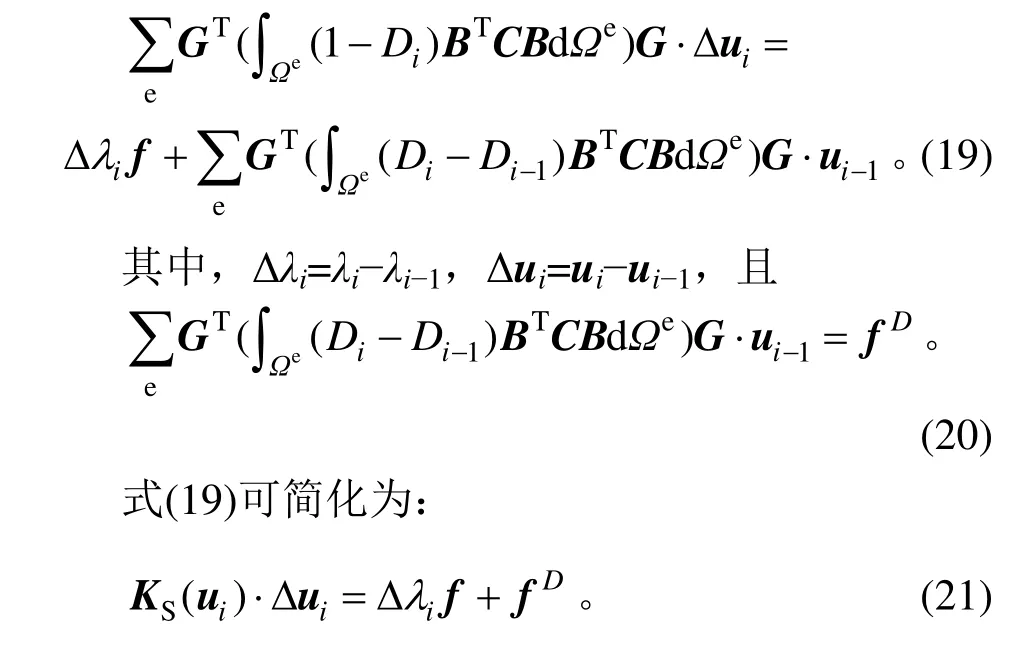
式(15)，(21)具有相同的形式，均由KS(u)和Df表达。因此，正割刚度-附加荷载法的增量平衡方程，已从2 个不同的角度完成推导。

为了提高SSALM 法的求解精度，可以在增量步内加入平衡校正的迭代步[13]。通过将式(15)或式(21)与迭代技术相结合，得到新的增量迭代方程：

式中：j为迭代次数；i为增量步。

由于引入了荷载因子λ，式(22)多出的一个未知量需要补充一个约束方程。该弧长形式的约束方程[15]为：

式中：l为规定弧长。

Crisfield[16]等人提出过其他类型的约束方程。本研究采用最经典的弧长迭代法。

SSALM 法由KS(u)来表达的，避免了在峰值点附近KT(u)病态化的现象。

将SSALM 法编入FORTRAN 有限元程序中，每个迭代步的收敛条件，采用位移判断准则。

3 试验算例

依托损伤杆的单轴拉伸和损伤梁的纯弯曲2 个试验算例，验证SSALM 法的精确性。

3.1 损伤杆模型的单轴拉伸

采用8 节点平面应变单元，建立损伤杆单轴拉伸的有限元模型，共12 609 个节点和4 096 个单元。杆左端完全固定，杆右端施加平行于杆轴的均布荷载q，如图1 所示。模型材料参数为：弹性模量E0=21.0 GPa，泊松比υ=0。采用与应变相关的损伤演化律：

式中：ε为单轴拉伸应变；κ=3.50×10−6为损伤参数。

图1 单轴拉伸损伤杆的有限元网格和边界条件Fig. 1 FEM mesh and boundary conditions of the damage bar

损伤杆的单轴拉伸有解析解。分别使用传统方法、SSALM 法和解析法，求出损伤杆的荷载-位移曲线，如图2 所示。从图2 中可以看出，传统方法出现了明显的漂移误差，即使改变增量步的步长，漂移误差并未改善。而采用SSALM 法，所模拟的结果，与解析解非常吻合。表明：传统增量迭代法发生了无法迭代消除的漂移误差，而SSALM 法可以跟踪到结构的真实响应。

3.2 损伤梁模型的纯弯曲

图2 单轴拉伸损伤杆模型的载荷-位移曲线Fig. 2 Load-displacement curves of the uniaxial tension of damage bar

悬臂梁的纯弯曲有限元模型如图3 所示，采用与损伤杆单轴拉伸的有限元模型相同的网格。梁的左端完全固定，梁的右端施加了大小为M的弯矩。模型材料参数为：弹性模量E0=21.0 GPa，泊松比υ=0。采用了与应力相关的损伤演化律。损伤变量定义(损伤演化方程式)为：

式中：为损伤力学中所定义的有效应力，κ=5.0×105Pa 为损伤参数。

该纯弯梁的解析解在文献[17]中已经给出。

图3 纯弯曲损伤梁的有限元网格和边界条件Fig. 3 FEM mesh and boundary conditions of the damage cantilever beam

考虑到圣维南原理(远离右端的横截面，受边界效应的影响不大)和纯弯曲的变形特点，远离右端的任意截面，具有相同的损伤分布。本算例取中间横截面，分析其损伤分布和变形。

根据SSALM 法和解析法，得到梁的中间横截面的损伤分布，如图4 所示。从图4 中可以看出，受压区无损伤发生，受拉区的损伤发展与梁的深度d成线性关系。梁的中性层随着外加弯矩M的增大，逐渐下移。最大损伤Dmax出现在梁顶。这些规律与式(25)一致，且与实际结果相吻合。采用SSALM 法得到的结果与解析解非常吻合。

图4 梁中间横截面损伤分布Fig. 4 The distribution of damage in the cross section of the beam

图5 弯矩M 与最大损伤Dmax 的曲线关系Fig. 5 The bending moment M-maximum damage Dmax curves

梁顶最大损伤Dmax与外部施加弯矩M之间的关系，如图5 所示。从图5 中可以看出，传统增量迭代法追踪的平衡路径与解析解偏离的非常严重。而SSALM 法精确地捕捉到了结构的真实平衡路径，不会出现迭代无法消除的漂移误差。

4 传统法和SSALM 法对比分析

通过对比分析传统增量迭代法和SSALM 法，分析引起传统增量迭代法误差的原因和SSALM 法如何修正该误差。

式(6)的增量应力-应变关系，由式(3)得到表达式(26)或(27)为：

比较式(7)与式(27)可知，ε·ΔCD项在式(7)中被忽略。传统的损伤有限元法，由于忽略掉了 ε·ΔCD项，其精度必然会下降。而在SSALM 中，被忽略掉的ε·ΔCD项，被转化成附加荷载f D，引入到增量平衡方程之中，克服了传统方法所产生的漂移误差。

传统增量迭代法与SSALM 的相互关系，如图6 所示。虚线和空心点表示传统增量迭代法的结果和路径；点划线和实心点表示SSALM 的结果和路径。

在增量步内利用迭代技术，可消除部分漂移误差，将图6 中空心方点校正到空心圆点。

图6 传统法和SSALM 法的误差对比分析Fig. 6 The error contrastive analysis in two different incremental-iterative methods

由式(29)可以知，传统增量迭代法中，由于忽略 ε·ΔCD，产生了漂移误差(模型误差)，该漂移误差可以通过引入fD有效消除，使得损伤有限元分析更贴近真实解。表明：SSALM 法将KT对应的增量位移，分解为KS对应的增量位移和fD对应的增量位移2 个部分。

5 结论

1) 在进行损伤非线性分析时，传统的增量迭代算法，会产生迭代无法消除的漂移误差。

2) SSALM 法可以精确地捕捉到结构的真实平衡路径，不会出现迭代无法消除的漂移误差。

3) SSALM 法将KT对应的增量位移分解为KS对应的增量位移和fD对应的增量位移2 个部分。