基于经验强度准则的岩体力学参数敏感性分析

2020-10-24张永杰马文琪罗伟庭蒋莉斌岳强

交通科学与工程 2020年3期

张永杰，马文琪，罗伟庭，蒋莉斌，岳强

(1. 长沙理工大学土木工程学院，湖南长沙 410114；2. 中国建筑第五工程局有限公司，湖南长沙 410004)

岩体抗剪强度参数是岩体稳定性评价的重要力学参数之一，其测定与取值将直接决定工程评价结果的有效性[1]。由于工程地质条件、试验误差等不确定因素的制约，导致岩体力学参数测定值具有很大的离散性[2]。经验估算法应用于实际工程也取得了良好的效果。苏永华[3]等人提出了表征岩石风化状况的定量指标，对地质强度指标(Geological Strength Index，简称为GSI)取值进行量化，确定公路隧道围岩的力学参数。武雄[4]等人通过对节理岩体的连通程度和空间产状的宏观判断，建立了工程岩体强度法(Geology, Mechanics and Engineering Method，简称为GMEM)。张永杰[5]等人基于岩体力学参数取值的随机性与模糊性，运用GSI取值系统与区间理论，对Hoek-Brown 强度准则进行优化改进，能更好地反映岩体破坏的非线性特征。於汝山[6]等人提出岩体完整性系数的定量指标，对GSI取值中的岩体结构面进行定量化描述。杨欢[7]运用Geo-Slope 极限平衡软件，分析了GSI等参数对岩质边坡安全系数的影响程度，并优化了锚索加固边坡的措施。王新刚[8]等人通过改进GSI量化取值，从而保证岩体力学参数定量化取值的合理性。黄阜[9]等人以长沙地铁二号线为工程背景，利用有限差分软件，分析了盾构隧道开挖面安全系数、支护力及Hoek-Brown 强度准则参数的关系。这些研究主要集中在地质强度指标的量化、修正及应用，而针对岩体基础地质力学参数对岩体工程稳定性影响方面研究鲜见。因此，本研究基于岩体GSI取值量化方法，拟对岩体力学参数的影响因素进行敏感性分析，并分析各因素对岩质边坡安全系数的影响规律。

1 基于GSI的岩体抗剪强度确定方法

Hoek 等人经过试验研究，建立了基于GSI的Hoek-Brown 强度准则[10]，其表达式为：

式中：σ1,σ3分别为岩体破坏时最大、最小主应力，MPa；σc为岩石的单轴抗压强度，MPa；mi为反映岩石软硬程度的材料参数，取值范围为5～40；D为节理岩体扰动系数[2]；a为与岩体特性相关的参数；mb为无量纲常数。

通过对Hoek-Brown 强度准则进行最佳拟合，可得到岩体等效的黏聚力c与内摩擦角值φ[10]：

侧限应力的上限值σ3max可由式(4)，(5)确定[10]：

1) 深埋隧道侧限应力的上限值：

2) 岩质边坡侧限应力的上限值：

式中：γ为岩体重度，kN/m3；H为岩质边坡高度或隧道埋深，m；σcm为岩体抗压强度，MPa。

岩体抗压强度可通过Mohr-Coulomb 强度准则确定[10]，其计算式为：

2 岩体GSI 取值量化指标的确定

在岩体力学中，节理特征系数Jc可通过节理起伏系数Jw、节理粗糙系数Js及节理蚀变系数Ja来确定[11]。其表达式为：

对于3 组或3 组以上的连续节理所切割成的岩块，其体积数计算式为[13]：

式中：Vb为岩块体积数；γi为节理组间夹角；Si为节理平均间距。

参数Jw,Js,Ja,Vb,γi及Si的取值见参考文献[10]，[12]。

Cai[14]等人根据大量岩体工程实践，提出了基于节理特征系数与岩块体积数的方法，共同量化地质强度指标取值。其计算式为：

3 岩体力学参数影响因素分析

选取实际工程中常见的花岗岩、砂岩及大理岩作为研究的对象，分别代表岩浆岩、沉积岩及变质岩3 类岩石。其强度参数的选取根据文献[15]，其具体取值见表1。在保证其他参数不变的情况下，将不同基础地质参数，代入公式(1)～(9)进行计算，并绘制成图1～5 的关系曲线。

从图1 可以看出，节理蚀变系数的增大，黏聚力增大而内摩擦角减小。对于花岗岩，当节理蚀变系数为2～3 时，黏聚力增加了21.9%，内摩擦角减小了27.9%，各自表现出对参数Ja强烈的敏感性。

表1 强度参数取值Table 1 Strength parameters

图1 节理蚀变系数对抗剪强度参数的影响Fig. 1 Effect of joint alteration coefficient on shear strength parameters

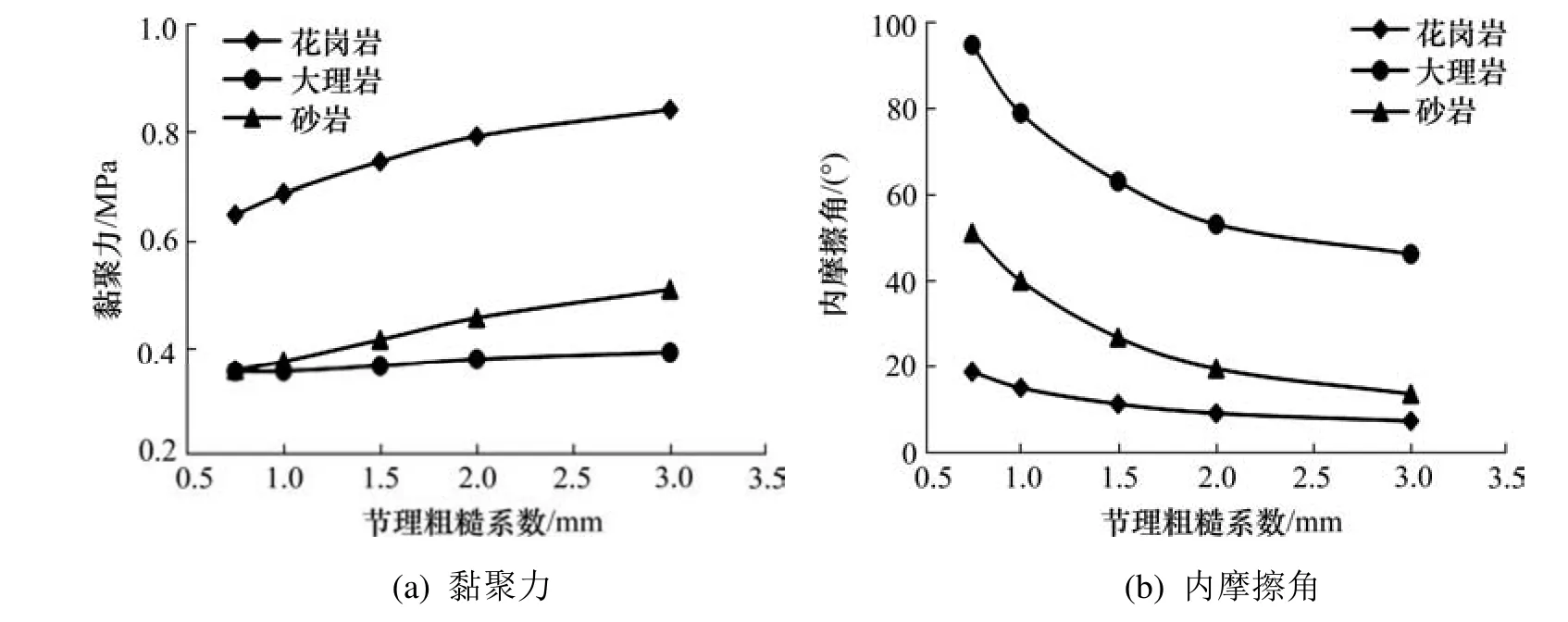
图2 节理粗糙系数对抗剪强度参数的影响Fig. 2 Effect of joint roughness coefficient on shear strength parameters

从图2 可以看出，节理粗糙系数的增大，黏聚力增大而内摩擦角减小。当节理粗糙系数为1～1.5 cm 时，花岗岩的黏聚力增加了8.5%，大理岩的内摩擦角减小了20.1%，各自表现出对参数Js强烈的敏感性。

从图3 可以看出，节理起伏系数的增大黏聚力增大，而内摩擦角减小。当节理起伏系数为2.5～3 m 时，砂岩的黏聚力增加了10.5%。而当节理起伏系数为1～1.5 m 时，大理岩的内摩擦角减小了15.1%，各自表现出对参数Jw强烈的敏感性。

从图4 可以看出，节理平均间距的增大，黏聚力增大而内摩擦角减小。当节理平均间距为600～700 mm 时，大理岩的黏聚力，增加了5.5%，花岗岩的内摩擦角，减小了14.1%，各自表现出对参数S强烈的敏感性。

图3 节理起伏系数对抗剪强度参数的影响Fig. 3 Effect of joint undulation coefficient on shear strength parameters

图4 节理平均间距对抗剪强度参数的影响Fig. 4 Effect of joint average spacing on shear strength parameters

图5 节理组间夹角对抗剪强度参数的影响Fig. 5 Effect of angle between joint groups on shear strength parameters

从图5 可以看出，节理组间夹角的增大，黏聚力和内摩擦角均随之减小。当节理组间夹角为40°～50°时，大理岩的黏聚力，减小了5.3%，花岗岩的内摩擦角，减小了14.6%，各自表现出对参数γ强烈的敏感性。

从图1～5 可以看出，当节理蚀变系数为4～8、节理粗糙系数为2～3 cm、节理起伏系数为2～3 m、节理平均间距为900～1000 mm 和节理组间夹角为60°～80°时，各地质基础参数对黏聚力或内摩擦角影响较小。表明：主观因素导致的偏差对岩体力学参数取值影响不大。如果超出该范围，则应谨慎判断参数取值的大小。

4 工程分析

计算模型采用单层均质岩坡(如图6 所示)，坡高12 m，坡比1:2，不考虑地下水作用。该岩质边坡参数：弹性模量为550 MPa，节理起伏系数为3 m，泊松比为0.25，节理平均间距为500 mm，节理组间夹角为50°，节理蚀变系数为4，容重为22 kN/m3，岩石材料参数取15，地质强度指标取55，岩体扰动参数取0.5，节理粗糙系数取3 cm，岩石单轴抗压强度取80 MPa。通过Rocscience Slide 软件进行计算，得到边坡安全系数FOS为1.845。

图6 二维岩质边坡模型(单位：m)Fig.6 Two-dimensional rock slope model (unit: m)

岩质边坡安全系数与基础地质参数、Hoek-Brown 强度准则参数密切相关。因此，将计算得到的边坡安全系数作为基准值，并按±20%，±15%，±10%，±5%的变化率，改变其中一个参数，其他参数不变，按照该方法，计算岩质边坡安全系数变化率，如图7 所示。

从图7(a)可以看出，各参数的变化，岩质边坡安全系数变化率大致呈线性关系。敏感性大小顺序为：地质强度指标＞扰动系数＞岩石单轴抗压强度＞岩石材料参数。当地质强度指标取值在基准值±20%范围内变化时，边坡安全系数为−19%～27%时，二者呈显著正相关。由于GSI＞70 或D为0.6～1 时，其对岩体力学参数取值及岩质边坡稳定性分析结果的影响较大[16−17]。因此，应增加GSI与D的测试范围，获取更多测试数据，减少分析误差。

图7 参数与边坡安全系数变化关系曲线Fig.7 Relation curve between parameters and slope safety factor

从图7(b)中可以看出，基础地质参数对岩质边坡安全系数影响的敏感性大小顺序为：节理蚀变系数>节理组间夹角>节理起伏系数>节理粗糙系数>节理平均间距。以线段的斜率表示敏感性系数的大小，计算得出当节理蚀变系数为4～8、节理组间夹角为60°～80°、节理起伏系数为2～3 m、节理粗糙系数为2～3 cm 和节理平均间距为900～1 000 mm时，边坡安全系数则稳定在±5%范围内。表明：主观因素导致的偏差，对岩质边坡稳定性分析结果的影响较少，超出该范围时，则应谨慎判断参数取值的大小。