粉质黏土原位地震动参数测试及模型参数反演分析

顾伟杰，范明桥，吉恩跃，钱 彬，张兴刚

(南京水利科学研究院，江苏 南京 210029)

土体的动力特性是岩土工程地震安全评价的重要基础，也是众多岩土工作者的研究重点和热点。为了描述土体动力响应过程，大多采用等效线性化的方法，即建立动剪切模量、归一化剪切模量G/Gmax与剪应变的关系[1-2]，目前多采用室内试验（如动三轴试验、共振柱试验）方法来获得上述曲线关系。

为了真实反映土体在天然状态下的动力特性，许多学者试图通过建立室内试验与现场测试的关系，对室内试验结果进行修正从而得到土体原位动力参数。刘振平等[3]基于室内试验对土石坝动力参数进行了反演，所得反演参数基本在经验值范围之内。李晶晶等[4]通过共振柱试验获取室内G-γ 衰减曲线和地震扁铲侧胀试验获得的参数来推求膨胀土原位G-γ 衰减曲线。然而，由于土样在取样过程中存在一定的扰动，破坏了原土层的结构性，因此室内试验结果相比于原位测试结果存在明显的差异，即不能真实反映土体的动力特性。如刘振平等[3]发现室内动三轴试验得到的堆石料最大动剪切模量系数K 值偏小；Amoroso 等[5]研究发现在相同应力历史下，膨胀土原位剪切模量较室内共振柱试验得到的剪切模量大，且随着应变的发展衰减更快。

综上，目前原位土动力参数的准确获取较为困难，且通过室内试验结果推求原位结果的方法不可避免地存在误差。因此，为了获得原位土动力参数，有必要开展土体的原位动力特性试验。本文介绍了自行研发的土体现场动力特性试验设备及其组成和工作原理，基于该试验系统，对南京地区某粉质黏土进行现场剪切模量试验，并采用遗传算法对所得数据进行反演得到原位模型参数。

1 地震动力参数原位试验测试系统

地震动力参数原位试验测试系统由可移动系统、荷载伺服系统、动力反应系统和数据采集系统四部分组成（图1）。

图1 地基动参数原位试验系统Fig.1 The in-situ ground motion parameters test system

该系统上配备了一个液压伺服振动器，可在预设的频率、振幅、加载循环次数及振动方向下将动荷载施加到刚性板上，从而传播到地基土体内。试验系统垂直加载单元可实现的最大试验荷载：静荷载为100±0.5 kN，动荷载为80±0.8 kN。预先埋设的传感器感受到被测信息后，经数据采集系统转换为某一固定形式的信号输出，可对其进行数据处理和基本分析。

该系统适用于各种地基场地的地震模拟，可在一定静力荷载作用下对地基施加水平向或垂直向动荷载（荷载的频率和振幅均可调），实时获得原位土的动力响应[6]。

2 试验方案及试验结果

2.1 试验场地及物理性质

本次试验针对南京某地区工程场地地基土，根据现场勘察结果，地表以下5 m 为均质土体。该场地地基土为黏土，呈黄褐色，含水率为20.2%，重度为18.3 kN/m3，塑性指数为22.6，黏聚力为75 kPa，内摩擦角为30°。

2.2 试验原理

荷载施加装置安装在桩基础的顶部（现场布置示意如图2 所示），振动器的液压系统用于施加静荷载，然后使用伺服液压振动器以试验拟定的振幅、频率和循环次数施加正弦水平动态荷载。此正弦水平荷载会产生垂直传播的剪切波，从而在土中产生动剪切应变。利用嵌入土壤中的地震检波器（S1-S2和S3-S4）测量土中传播的剪切波。在恒定的静态压力下，水平动荷载的幅值逐渐增加，在土中引起逐渐增大的剪切应变，从而建立两者关系。最后，在不同应力水平下重复此过程，得到不同应力下土体的非线性剪切模量和归一化剪切模量。

图2 桩基础和传感器布置（单位：mm，S 代表检波器）Fig.2 The layout of pile foundation and sensor (unit: mm)

使用地震检波器的时间记录计算相邻地震检波器之间的平均剪切波传播速度。通过将传感器之间的水平距离除以传播时间来计算土壤中相邻传感器之间的平均横波速度。然后根据剪切波速度Vs和土壤密度ρ 计算剪切模量，如式(1)所示：

对记录的速度-时间历程进行数值积分，得到位移-时间历程，计算出相邻传感器位移-时间历程的峰值位移。利用式(2)计算剪切应变：

式中：γ12为相邻传感器之间的平均剪切应变；u1为靠近桩基础侧的传感器记录的峰值位移；u2为在同一时间用另一个传感器记录的位移。这里假定了位移与相邻传感器之间的距离呈线性关系。

2.3 试验内容及结果分析

Wong 等[7]研究发现，循环次数为15 次、频率为5.0 Hz 时通常会产生良好的正弦输出信号。因此本试验拟定的循环次数为15 次，频率为5.0 Hz。具体加载方案如表1 所示[8]。

以1 号加载方案为例，试验测得S1-S2 土层剪切波波速Vs为247 m/s，取位移-时间曲线波形良好区段如图3 所示，应用式(1)及(2)得本次加载方案的动剪切模量G 为110 MPa，剪应变γ 为1.5×10−5。

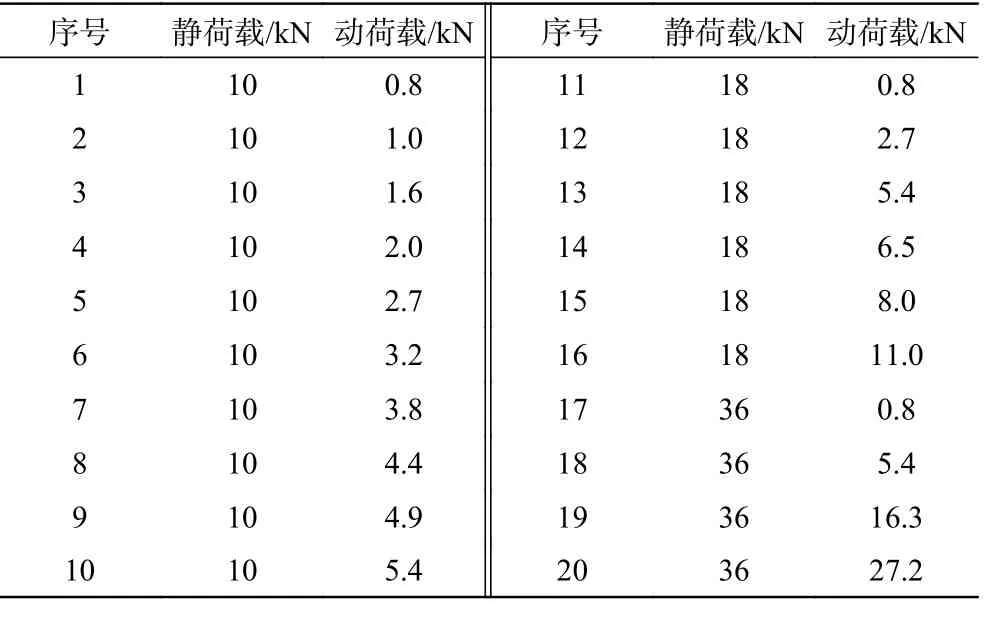
表1 现场测试的加载方案Tab.1 Field loading plan

图3 位移-时间曲线Fig.3 Relationship between u and t

待试验全部完成后，建立动剪切模量和归一化剪切模量随剪切应变的变化关系，分别如图4 和图5所示。

图4 动剪切模量-剪应变曲线Fig.4 Relationship between G and γ

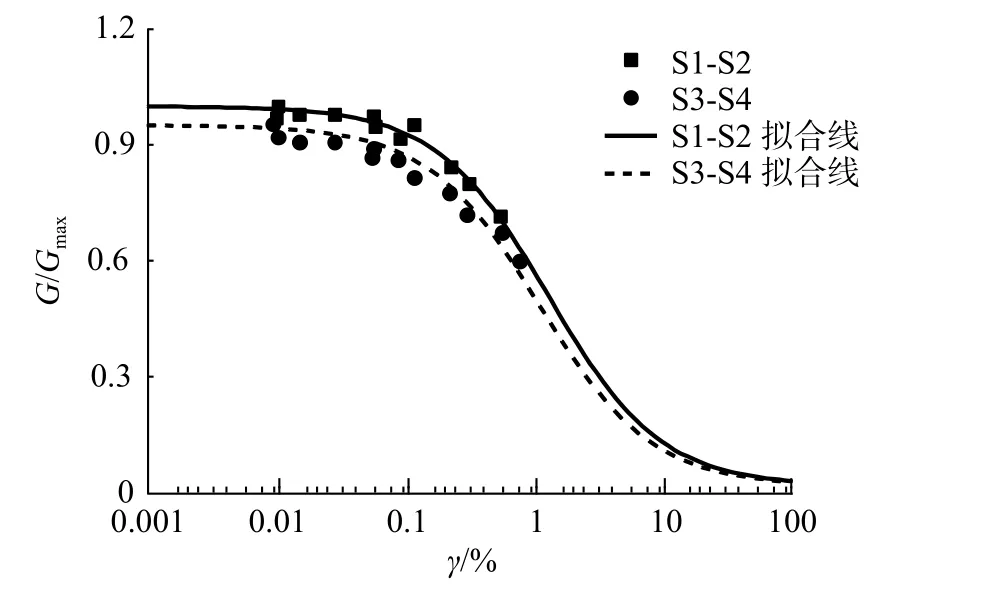
图5 归一化剪切模量-剪应变曲线Fig.5 Relationship between G/Gmax and γ

由图4 和图5 可见，动剪切模量和归一化剪切模量均随动剪应变的增大而减小，所得试验结果符合大量试验资料统计变化规律[9]。对比发现，传感器S1-S2 之间土的动剪切模量相比于S3-S4 之间土的动剪切模量大，高志兵等研究发现土的Gmax随埋深的增大而增大，在统计意义上与深度存在指数关系[10]；S1-S2 土层的动剪切模量比值也要较S3-S4 土层稍大，这是因为动剪切模量比与剪应变的关系曲线主要受土体有效围压的影响[9]。

由图5 可以发现，动剪切模量G 随剪应变γ 的增大而减小，表明土在周期荷载作用下动应力-动应变关系具有显著的非线性。分析可知：当剪应变小于0.1%时，曲线衰减速度较慢；而当剪应变大于0.1%时，动剪切模量减小的速度愈来愈快，原因是当施加的动荷载逐渐增大时，土体开始出现塑性变形，后续动荷载下的滞回圈将不再封闭且向应变增大的方向移动，显示出应变逐渐累积的特性[9]。

3 基于遗传算法的G/Gmax-γ 模型参数反演

3.1 遗传算法介绍

为研究该地区粉质黏土的G/Gmax-γ 拟合曲线的模型参数取值范围，采用遗传算法对所得数据进行反演。

遗传算法是一种进化算法[11]，其基本原理是按照生物界中“适者生存、优胜劣汰”的原则，将问题参数编码为染色体，通过多次迭代更新染色体信息以逼近问题的最优解。

3.2 模型参数计算

目前，对G/Gmax-γ 关系进行理论公式描述的有Hardin-Drnevich 方程和Martin-Davidenkov 方程等。本文选用Martin-Davidenkov 模型，如式(3)所示：

式中：A，B，γ0为模型参数。

现对两个土层分别进行计算，将式(3)算得的动剪切模量比与动剪切模量比实测值之差的平方和作为目标函数，以目标函数值最小为标准来求取参数取值，如式(4)所示：

式中：Ki和Ki*分别为第i 点数据所对应的动剪切模量比的实测值和计算值。

遗传算法的部分参数定义如下：种群大小为50 个，迭代次数取100 次，交叉概率取0.6，变异概率取0.001，参数A，B，γ0的取值范围[12]为A∈（1.0，1.6），B∈（0.5，0.61），γ0×104∈（60，70）。

两土层目标函数值与迭代次数的关系如图6 和7 所示。可以看出，目标函数随迭代次数的增加逐渐收敛，大约经过20 步的迭代计算就能得到比较稳定的值。

利用上述方法对试验地区粉质黏土不同埋深的土层进行重复试验，可得各深度区间内的具体参数反演结果详见表2。

由表2 可以发现，参数A 随深度的增大呈逐渐减小的趋势，且减小幅度越来越小，即A 受土层埋深影响越来越弱，相比较参数B 和γ0则变化范围不大，分析认为主要与土层物理力学性质有关。Martin-Davidenkov 模型在该试验地区较浅土层内的模型参数取值范围：A∈（1.04，1.15），B∈（0.50，0.61），γ0×104∈（68.5，68.7），试验结果可为相关工程提供一定的参考。

图6 S1-S2 土层目标函数值与迭代次数的关系曲线Fig.6 Objective function values with iterations in S1-S2

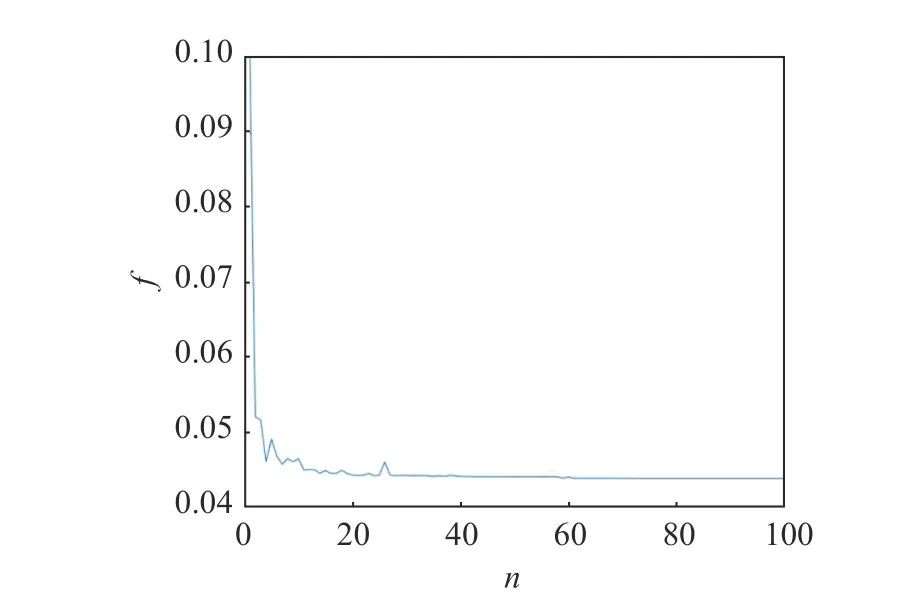
图7 S3-S4 土层目标函数值与迭代次数的关系曲线Fig.7 Objective function values with iterations in S3-S4

表2 两土层G/Gmax-γ 模型参数及目标函数值Tab.2 G/Gmax-γ model parameters and objective function values in two soil layers

4 结 语

介绍了自行研发的地震动力参数现场试验系统，该系统具有应用范围广、可控性强、可靠性高等特点，利用该系统可测得现场原位的G-logγ 和G/Gmax-logγ 曲线。试验结果表明：剪应变小于0.1%时，曲线减小速度较慢；当剪应变超过0.1%后，随剪应变的增大，动剪切模量减小的速度变快，表明土的动应力-应变关系具有非线性和应变逐渐累积的特点。

引入Martin-Davidenkov 模型，采用遗传算法对所得试验数据进行反演分析，得到了该试验地区较浅土层内的模型参数取值范围，可为相关工程提供一定参考。