缝面水压力与地震作用下重力坝坝踵裂缝扩展数值模拟

胡良明，李姝钰，贾 欣，杨 旭

(郑州大学 水利科学与工程学院，河南 郑州 450001)

混凝土重力坝基本都是带缝工作，且混凝土重力坝坝踵处于不同材料的交界处，承受高水头作用，受力条件复杂。我国混凝土重力坝大部分建设在地震频发的西南地区，若重力坝遭遇强烈地震，裂尖容易因应力集中而产生贯穿性裂缝[1]，因此需要对地震和缝水压力作用下坝踵裂缝扩展进行数值模拟。用传统有限元框架模拟裂缝扩展需不停地进行网格重剖，Belytschko 等[2]提出的扩展有限元法（XFEM）裂缝网格与计算网格相互独立，不要求网格重剖便可模拟裂缝扩展；杜效鹄等[3]用XFEM 对重力坝断裂问题进行了数值分析；方修君等[4-5]用XFEM 进行了Koyna 重力坝地震开裂过程的模拟和水压作用下混凝土试件开裂过程模拟；董玉文等[6]建立了适用于重力坝水力劈裂的XFEM；高景泉等[7]进行了静力作用下坝踵裂缝的水力劈裂分析，未考虑地震作用；钟红等[8]基于多边形比例边界有限元法研究了坝基开裂与缝内水压力分布形式的关系；郑志芳等[9]研究了地震作用下缝内水压规律及其对裂尖应力强度因子的影响，为地震作用下坝体水力劈裂研究奠定了基础。

以上学者在混凝土重力坝裂缝扩展模拟中，简化了重力坝的受力状态与坝踵初始裂缝状态，没有考虑缝面水压力与地震的综合作用，不能真实模拟坝踵裂缝扩展最危险的应力及位移情况。基于此，本文利用XFEM 和相互作用积分理论，建立重力坝坝踵存在初始裂缝的条件下，考虑缝面水压力与地震共同作用的裂缝扩展数值模型，分析坝踵初始裂缝长度、坝体与坝基弹模比与缝面水压力分布形式对坝踵裂缝扩展的影响。

1 裂缝动态分析基本原理

1.1 动态断裂问题的XFEM

位移场u 的表达式参考文献[10]及[11]。动态断裂问题的裂尖增强函数为：

式中：r，θ 分别为裂尖局部极坐标的半径和夹角。

动态断裂问题控制方程：

动态断裂问题进行时间积分时选用常用的Newmark 隐式积分：

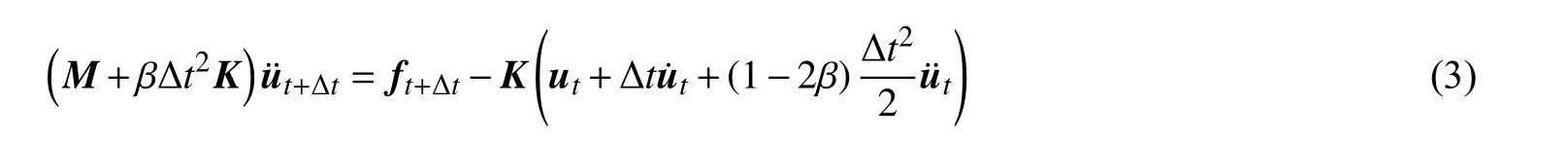
式中：Δt 为时间增量；ut为t 时刻的位移向量；当 α ≥0.5且 β ≥0.25(α+0.5)2时，此算法无条件稳定，本文取α=0.5，β=0.25。

1.2 动态裂缝扩展准则

选择最大周应力准则作为裂缝开裂准则。裂缝扩展角 θc满足：

等效应力强度因子Keq满足：

若Keq大于动态断裂韧度 KICdyn，则裂缝开始扩展。

动态断裂问题求解应力强度因子采用相互作用积分法。在考虑体积力、惯性力以及缝面作用力的情况下，相互作用积分I(1,2)表达式为：

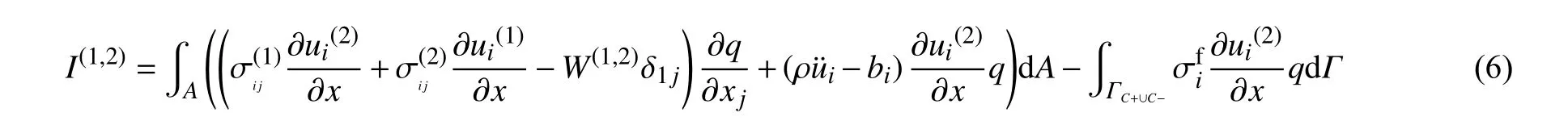
式中：I(1,2)为状态1 和2 的相互作用积分；q 为权函数；W(1,2)为状态1 和2 下的应变能；为裂缝面牵引力在i 方向的分量。

相互作用积分和裂尖动态应力强度因子Kdyn的关系为：

2 数学模型

2.1 有限元模型的建立

Koyna 混凝土重力坝建在印度Koyna 河上，该坝于1967 年经历的6.5 级强烈地震中保留了完整的强震破坏记录，因此常被用于大坝的抗震分析。大坝的基本情况及坝基的计算范围如图1(a)所示。坝踵位置预设一条长度为a 的水平裂缝。

坝体混凝土及基岩的泊松比均取0.25，平面应变断裂韧度KIC均取5 MPa·m1/2，坝体混凝土的弹性模量E1取31 GPa，密度取2 450 kg/m3，基岩的弹性模量设为E2。XFEM 数值分析采用四节点等参元均匀网格，计算模型共划分为3 440 个单元，有限元网格划分如图1(b)所示。地基采用无质量地基模型，避免地震波在坝基中产生传播放大效应。采用Wester-gard 附加质量法来进行重力坝抗震设计中动水压力的模拟，以附加质量形式施加到结构自由度质量矩阵。文献[12]中线弹性应力强度因子适用于大体积混凝土结构的观点是目前广泛接受的，以此为依据建立重力坝坝踵裂缝断裂数值模型。

图1 重力坝计算模型及网格划分示意Fig.1 Gravity dam calculation model and grid partition schematic diagram

2.2 地震波的选取

由于人工波不具备天然波的完全非平稳随机过程特性，缺少强烈变化的短周期成分，结合《水工建筑物抗震设计规范》(GB 51247—2018)，按照Ⅱ类场地，选取最大加速度值为0.167g、特征周期0.35 s、荷载增量步为0.1 s 的天然波TH2TG035，水平方向加速度时程曲线见图2，前17 s 加速度变化幅度较大，故截取前17 s 用于计算。

图2 地震波加速度时程曲线Fig.2 Time history graph of seismic wave acceleration

2.3 计算工况

模拟试验采用的各项数据如表1 所示，缝面水压力为结构所受外荷载，作为施加在裂缝面上的面力。假定缝面水压力P 的分布形式为：

式中：r 为缝面上的节点与裂尖的距离；a 为裂缝长度；P0为裂缝口的静水压力。

参考文献[13]，水压力分布形式中，n=0，1，2 时分别代表水压力均匀分布、线性分布和二次函数分布。模拟重力坝坝踵裂缝在最不利工况下的裂缝扩展，即考虑缝面水压力、坝体自重和地震共同作用下，上游坝面承受满水库动水压力，下游无水。计算共分为5 种工况，具体见表1。

表1 计算工况Tab.1 Calculation conditions

3 计算结果分析

3.1 等效应力强度因子及裂缝扩展路径时程分析

地震加载过程中，缝面水压均匀分布、初始裂缝长度为5 m 且坝基与坝体弹模比为1 时的等效应力强度因子Keq见表2。图3 为各时刻坝踵裂缝形态及坝体-坝基体系x 方向最大主应力σxx。

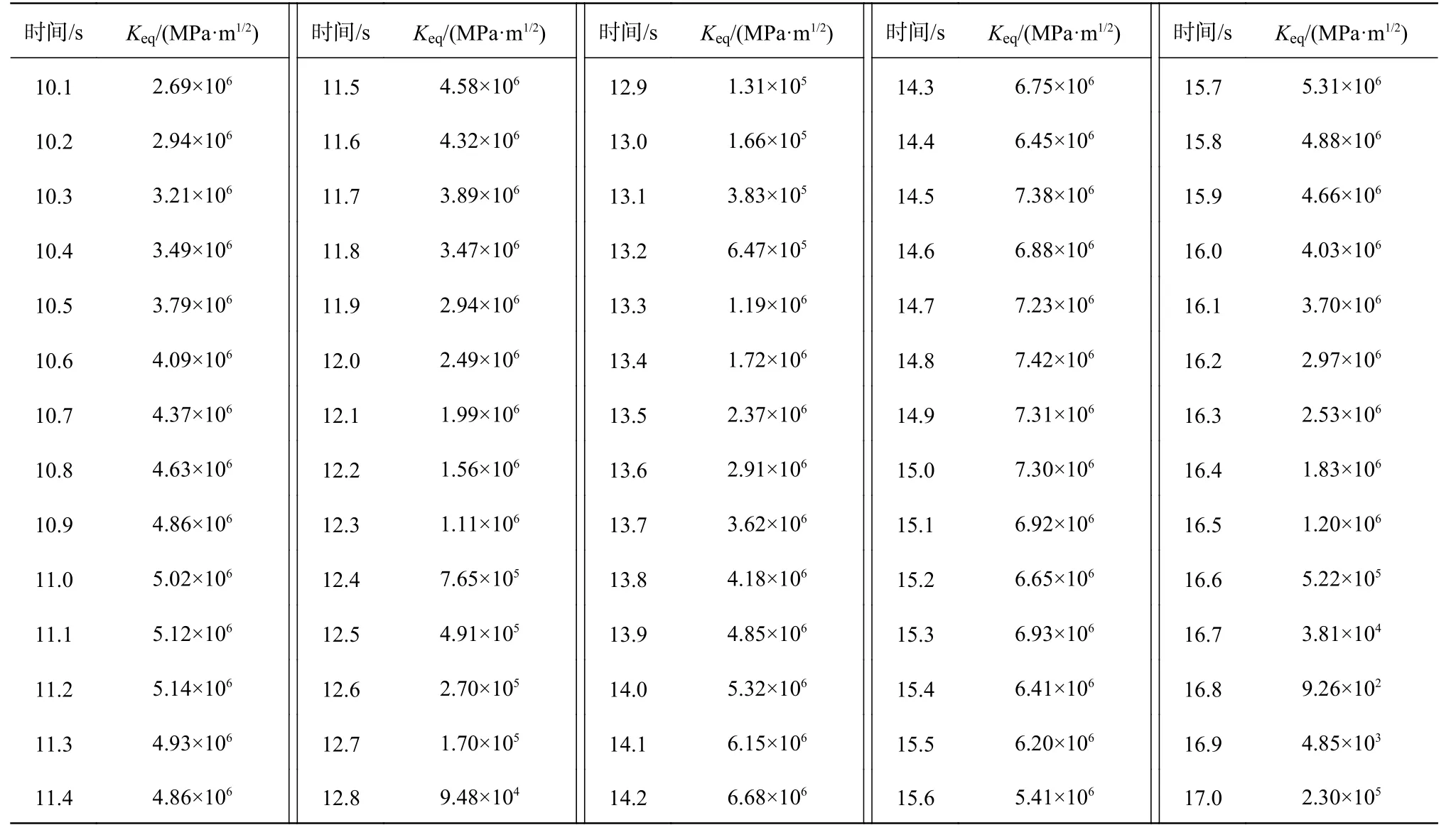
表2 等效应力强度因子KeqTab.2 Calculation table of equivalent stress intensity factor Keq

分析表2 及图3 可得：14.0 s 至15.7 s 期间Keq值大于KIC（=5 MPa·m1/2），持续时间较长。14.0 s 至14.8 s，Keq持续增大，14.0 s 时裂缝开始逐渐扩展，x 方向裂缝尖端处的拉应力随时间增加而增加，14.8 s 时裂缝加速扩展，x 方向的拉应力数值增加到最大值1.5 MPa，拉应力作用范围达到最大；14.8 s 至15.7 s，Keq逐渐减小，15.8 s 时Keq小于KIC，15.7 s 裂缝扩展长度与17.0 s 时的基本一致，此时裂缝尖端仍有较小的拉应力，在17.0 s 时裂缝尖端为压应力，应力逐渐趋近稳定，符合文献[13]中对裂尖应力状态的描述。裂缝扩展过程中，在动水压力和自重作用下初始裂缝不断向坝基扩展，裂缝尖端产生了明显的拉应力集中现象。

图3 x 方向最大主应力云图(单位：Pa)Fig.3 Maximum principal stress of x (unit: Pa)

3.2 不同弹模比对裂缝扩展路径的影响分析

图4 给出了不同工况下的裂缝扩展路径。从图4 可见，不同初始裂缝长度下，裂缝扩展长度均随坝基与坝体弹模比的增大而减小，裂缝扩展路径与坝基面间的夹角逐渐减小，当坝基与坝体弹模比足够大时，裂缝不再发生扩展。从图4(d)可见，裂缝扩展路径随着初始裂缝长度的增加逐渐接近坝基面，初始裂缝长度为8 m 时裂缝扩展路径为先向坝基扩展再向坝体扩展，且初始裂缝的长度增加，裂缝扩展长度也随之增加。从图4(e)可见，随着缝面水压力分布系数n 的增加，缝面水压力减小，裂缝扩展长度减小，扩展路径向坝基扩展。

4 结 语

基于XFEM，建立了考虑缝面水压力和地震作用下的重力坝坝踵裂缝断裂数学模型。通过计算分析坝基基岩与混凝土坝体的弹模比、缝面水压力分布形式及初始裂缝长度等工况下的坝踵裂缝扩展路径，得出以下结论：

（1）裂缝的扩展长度随坝基与坝体弹模比的增大而减小，当坝基与坝体的弹模比足够大时，裂缝不会发生扩展；裂缝扩展路径与坝基面的夹角随坝基与坝体弹模比的增大逐渐接近坝基面。两者的共同作用减小了坝体发生深层滑动的风险。因此重力坝工程进行地基选择时，选择坝基弹性模量较大、基岩条件较好的地区可以有效防止重力坝发生滑动破坏。

（2）裂缝扩展长度随着初始裂缝长度的增加而增加；裂缝扩展路径随着初始裂缝长度的增加向坝基面延伸；当初始裂缝增加到一定长度时，裂缝先向坝基方向扩展然后转向坝体方向。两者的共同作用会使裂缝过长，导致重力坝坝体与坝基脱离，发生滑动破坏。

（3）随着缝面水压力系数n 的增大，裂缝扩展长度虽有所减小，但减小的幅度较小，而裂缝扩展路径与坝基面之间的夹角增大，削弱岩基稳定性，容易造成深层滑动破坏。由文献[13]可知，裂面水压力分布规律是影响缝面水压力对裂缝断裂特性的主要因素，因此考虑缝面水压分布的影响，可以有效提高数值模拟的精度。