基于Fisher-PCA 和深度学习的入侵检测方法研究

张鑫杰，任午令

（浙江工商大学计算机与信息工程学院，杭州，310018）

引 言

互联网技术的发展正潜移默化地改变着人们的生活方式，拉近了人与人之间的距离，给人们的生活带来了许多方便，但是任何事情都有两面性，随着网络的普及，通过网络进行攻击犯罪的事件也越来越多，一些勒索攻击在生活中已经屡见不鲜。面对日益严峻的攻击行为，人们需要研究并部署安全系统来保护自己的电脑和相关的服务器，而入侵检测系统（Intrusion detection systems，IDS）[1-2]作为一种检测是否存在外界入侵行为的预防手段，对维护计算机系统安全、确保网络的正常运行有着十分重要的意义[3-4]。

随着技术的发展，运用于入侵检测的方法也越来越多，从以前的基于规则进行检测[5]到传统的机器学习[6]，再到现在的深度学习，学者们已经做了大量的研究。比如文献[7]中提出通过遗传算法来寻找最合适的反向传播（Back propagation，BP）神经网络权值，对传统的BP 神经网络进行了改进，提升了整个网络的性能，但是在实际场景中数据的维数并不是固定不变的，如果数据的维数过高，冗余量大会导致整个网络的计算复杂度大大增加从而使检测的时间增加；文献[8]提出将模糊C 均值聚类（Fuzzy C-means，FCM）应用于入侵检测中，可以有效地检测出部分未知的攻击，并且适用于动态的网络环境，但是当数据类别较多时需要很长的计算时间；文献[9]提出通过信息增益（Information gain，IG）和主成分分析法(Principal component analysis, PCA)方法相结合进行特征提取，通过这种方法进行数据的降维有效地提高了分类模型的检测率，但在降低误检率上效果并不是很理想；文献[10]中提出使用Fisher-FCBF 算法来进行特征提取，虽然大大降低了模型的计算时间，但在准确率和误报率方面并没有提高；文献[11]中先根据属性比率数据特征提取方法进行数据处理，然后进行高斯混合聚类，最后使用随机森林进行分类，提高了准确率，但是聚类时k 值难以确定，聚类的好坏对分类结果有较大的影响；文献[12]提出通过独立成分分析（Independent component analysis，ICA）算法来进行特征提取，消除特征的冗余性，使模型具有更好的特征学习能力和更精确的分类能力。

综上所述，现有的入侵检测方法对数据进行特征提取后往往只对分类模型的准确率、误报率和检测时间等的某一方面做了改善，同时一些具有学习功能的方法在运行性能上也存在着不足。为此，本文提出了一种基于Fisher-PCA 和深度学习的入侵检测方法。通过改进的Fisher-PCA 特征提取方法，提高了入侵检测分类模型的准确率、检测率，降低了误报率；通过搭建具有收敛速度快、学习能力强等特征的深度神经网络（Deep neural networks, DNN）对数据进行分类，进一步提高了模型的运行性能；最后使用公开的KDD99 数据集对该入侵检测算法进行了测试，以验证算法的有效性。

1 基于Fisher-PCA 和深度学习的入侵检测模型

本文提出的一种基于Fisher-PCA 和深度学习的入侵检测模型，能够有效处理那些维度高、冗余量大的数据，并且在准确率和误报率上有较好的表现，其基本流程图如图1 所示。

首先对测试集和训练集中的数据进行预处理，将每条报文数据的符号特征数字化（包括类别），再对数据进行标准化处理，然后进行数据的Fisher 特征选择和PCA 降维，将其输入到设计好的DNN 神经网络中进行训练，多次训练后模型达到最优化，最后输入测试集得到结果并对结果进行规范化处理做出反应。

1.1 Fisher 特征选择

Fisher 特征选择算法的大体思路是借鉴了线性判别分析（Linear discriminant analysis，LDA）算法。LDA 是Fisher 于1936 年提出的一种有监督学习的降维方法，其思想是将样本点投影到一条直线上，使同类的样本点尽可能地集中，而使不同类的样本点尽量分离。下面给出如何找到这条直线的数学公式。

图1 基本流程图Fig.1 Basic flow chart

定义Sw、Sb和St分别表示类内、类间和总体散度矩阵，满足St=Sb+Sw，线性空间的某一条直线为向量W，则目标函数可定义为[13]

求解出J(W)的极大值W∗，则向量W∗就是所要求解的这条直线。

根据LDA 算法的思想可以得出如下结论：在同一特征下，当满足类间相似度越大，而类内相似度越小，说明该特征对于分类的有效性更高，该特征也就更加重要。Fisher 特征选择算法的伪代码如下。

输入：训练样本数据集。

输出：重新排列后的数据集。

（1）计算输入数据集的特征数n，类别数m。

fori=1：n

计算出每个特征的所有数据的平均值

forj=1：m

计算该特征值的所有类别各自方差，并把他们相加，表示类内方差temp1；

计算该特征值下每一类数据的平均值和样本总平均值的方差，将这些方差相加为类间方差temp2；

（2）计算特征重要性=temp2/(temp1+0.01)（避免temp1 为0）。

（3）按特征重要性降序排列。

1.2 PCA 降维

PCA[14]是一种统计学方法，其目的是如何以最少的信息丢失将原有的变量浓缩成少数几个因子（主成分），其具体的步骤如下。

（1）数据标准化，以消除量纲对数据的干扰。

式中：xij为矩阵中第i行第j列的值，μj和σj分别为第j维向量的均值和标准差，每个数据标准化后的结果为Zij。

（2）计算协方差矩阵S

（3）根据协方差矩阵S计算出对应的特征值(λ1,λ2,…,λp)和特征向量a1,a2,…,ap。

（4）根据得到的特征值计算贡献率η和累计贡献率∑η。

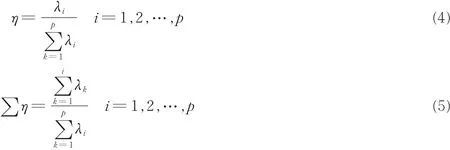
（5）确定累计贡献率大于某一值时满足要求，取出前k个特征值对应的特征向量a1,a2,…,ak组成p行k列的变换矩阵Q。

（6）得到降维后的k维数据矩阵T

1.3 DNN 深度神经网络模型设计

首先确定网络结构，设计了包含4 个隐藏层的DNN 模型，其中每一个隐藏层分别含有64 个隐藏单元，每一层训练的结果都作为下一层的输入。

使用线性整流函数（Rectified linear unit，ReLU）作为模型中间层的激活函数。引入激活函数的目的是为了增加神经网络各层之间的非线性关系而不是简单的矩阵相乘。与sigmoid 等其他一些激活函数相比，此激活函数不仅节省了计算时间，而且很好地解决了反向传播时常常出现的不稳定和梯度消失问题，其数学表达式为[15]

即当x≥0 时，f(x)=x；当x＜0 时，f(x)= 0，如图2 所示。

使用一种好的优化算法是深度学习模型的关键，本模型使用Adam 优化算法[16]来代替传统的梯度下降算法，与其他算法主要的区别在于为不同的参数设计独立的自适应学习率，其有着收敛的速度更快，所需内存更小，损失函数波动较小等优势，适合解决包含大规模数据和参数的优化问题。Adam 算法的核心步骤如下：

（1）计算开始t时间步的梯度

图2 ReLU 激活函数Fig.2 ReLU activation function

（2）计算梯度均值

（3）计算梯度平方均值

（4）对梯度均值mt偏差进行纠正，以降低对训练初期的影响

（5）对梯度平方均值vt偏差纠正

（6）更新梯度值（α为学习率，ε为默认常数）

最后一层采用Softmax 分类器，它是一种多类别分类器，将多个神经元的输出映射到[0,1]区间内，这些值的累加和为1（满足概率性质），最后选取出概率最大的结点作为分类结果。

2 实验过程及结果分析

2.1 实验环境

实验环境的各项指标为，CPU：3.30 GHz；内存：8 GB；显卡：Intel(R) HD Graphics 4600 (2112 MB)；OS：Windows7.0；开发环境：Pycharm 2019.1.2。

2.2 实验数据集

实验所使用的数据集是由KDD Cup99[17]提供的10% 训练样本和corrected 的测试样本，训练集数据共494 021 条，测试集数据共311 029 条。数据集中各个类型的数据分布如表1 所示。

2.3 数据预处理及结果分析

2.3.1 符号特征数字化

由于KDD99 数据样本的42 维特征中，某些特征的值不是数值类型，所以要将其先转为数字特征，通过如下方式处理：

表1 实验数据类型的分布情况表Table 1 Distribution of experimental data types

(1)协议类型：共有3 种，将其从0 开始递增顺序对其编码，即

Protocol_type={“icmp”：0；“tcp”：1；“udp”：2}

(2)目标主机的网络服务类型：共有70 种，从0 开始递增顺序对其编码，即

Service_type={“IRC”：0；“X11”：1；“Z39_50”：2；…}

（3）连接正常或错误的状态：共有11 种，从0 开始递增顺序对其编码，即

Connection_type={“OTH”：0；“REJ”：1；“RSTO”：2；…}

（4）攻击类型：即第42 维的攻击类型标签，将其分为5 大类，从0 开始递增序列对其编码，即

Lable_type={“Normal”：0；“Dos”：1；“Probe”：2；“U2R”：3；“R2L”：4}

原数据样例：

0,tcp,http,SF,181,5 450,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,8,8,0.00,0.00,0.00,0.00,1.00,0.00,0.00,9,9,1.00,0.00,0.11,0.00,0.00,0.00,0.00,0.00,normal

数字化后的数据样例：

0,1,22,9,181,5 450,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,8,8,0.00,0.00,0.00,0.00,1.00,0.00,0.00,9,9,1.00,0.00,0.11,0.00,0.00,0.00,0.00,0.00,0

2.3.2 数据标准化

因为数据之间的量纲和数值的量级不一样，所以如果不进行标准化会对模型训练时间和检测性能产生不小的影响。数据的标准化方法有很多种，本文所使用的标准化方法为min-max 方法，描述如下：定义序列x1,x2,…,xn公式为

yi的范围在0 到1 之间，且没有量纲。

标准化后的数据样例：

0,5.000 000 00e-01,3.333 333 43e-01,8.999 999 76e-01,2.610 417 77e-07,1.057 130 05e-03, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1.565 557 72e-02, 1.565 557 72e-02, 0, 0, 0, 0, 1, 0, 0,3.529 411 93e-02,3.529 411 93e-02,1,0,1.099 999 99e-01,0,0,0,0,0,0

2.3.3 Fisher 特征选择

使用Fisher 特征选择算法对训练集进行特征选择，得到每个特征索引号对应的评价函数值，然后根据所得的评价函数值由高到底对相对应的特征索引号进行排序如下: [20,21,23,12,24,2,36,32,3,29,39,25,26,38,4,31,37,34,35,1,33,6,22,19,8,10,30,17,18,14,16,15,11,41,27,28,13,7,9,40,5],本实验选取前35 个特征，组成新的35 维的训练数据集，对测试集也选取对应的特征集组成新的测试集。

2.3.4 PCA 降维处理

通过PCA 降维方法对Fisher 特征选择后的训练数据集进行降维，得到的累计贡献率与维数的关系如图3 所示。为了在降维的同时尽量保留原始记录的信息，取累计贡献率为99.9%，即取阵的前20 维作为新的训练数据集，保留了几乎全部原始数据集特征信息的同时达到降维目的，然后将训练数据集降维得到的变换矩阵对特征选择后的测试集降维。

2.3.5 实验结果及分析

采用准确率AC、检测率DR 和误报率FA 来作为评价指标，其计算公式为

图3 累计贡献率与维数关系图Fig.3 Relationship between cumulative contribution rate and the dimension

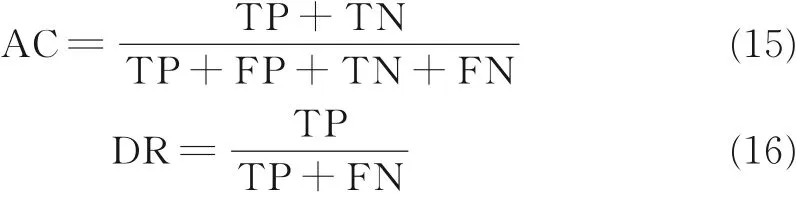
其中公式中各变量的含义如表2 所示。

这里将本文设计的DNN 模型命名为NDNN，将带有Fisher-PCA 特征处理功能的模型命名为FP_NDNN，时间为检测时间。这两种模型的指标对比如表3 所示。

表2 评价指标中各变量的含义Table 2 Meaning of the variables in the evaluation index

表3 NDNN 和FP_NDNN 模型的指标比较Table 3 Index comparison between NDNN and FP_NDNN models

由表3 对比可知，经过Fisher 和PCA 进行特征处理后的模型在准确率和检测率上有较小的提升，但在入侵检测中的重要指标误报率上有较大的降低，相比于NDNN 模型的误报率相对降低了77.2%。检测时间下降了25%。

FP_NDNN 模型与其他模型的指标对比如表4 所示。

表4 FP_NDNN 模型与其他模型的指标比较Table 4 Index comparison between FP_NDNN and other models

由表4 对比可知，本文模型FP_NDNN 与传统的机器学习算法支持向量机（Support vector machine, SVM）和传统的人工神经网络（Artificial neural network, ANN）相比，在各个性能上都有大幅度的提高；与通过PCA 对数据进行处理并结合卷积神经网络的PCA-CNN 算法相比，在准确率和检测率上不相上下，但是误报率下降了36%；与DBN4 算法相比可能在准确率和检测率上略有不足，但在误报率上下降了63%。

本文所采用的模型结构为64—64—64—64，不同的模型结构对实验结果可能会有不同的影响，一些不同的模型结构的指标比较如表5 所示。

表5 不同模型结构的指标比较Table 5 Index comparison of different model structures

由表5 对比可知：模型结构越复杂，其检测所需的时间也越长；在准确率和检测率上，第3 和第4 种模型要略好于第1 和第2 种；在误报率方面，不同的模型结构差别还是比较大，并不是越复杂的模型结构误报率越低，4 种模型结构中第3 种误报率最低，也是本文所采用的。

上述所分析的是模型对正常数据和攻击数据的检测效果，使用FP_NDNN 模型对不同攻击类型进行检测并与其他模型进行比较的结果如表6 和7 所示，评价指标与前面不同，这里所使用的准确率和漏报率的计算公式分别为

准确率=预测的攻击类型和实际的攻击类型相同的数目/预测为该攻击类型的数目

漏报率=把某类攻击样本预测为正常样本的数量/该类攻击样本的数量。

表6 对不同攻击类型检测的准确率Table 6 Detection accuracy of different attack types %

表7 对不同攻击类型检测的漏报率Table 7 False negative rates of different attack types of detection %

由表6 和7 结果对比可知：对于Dos 攻击类型的检测，3 种模型的检测效果都不错，并且指标也不相上下；对于Probe 攻击类型地检测，本文方法与GBDT 模型不相上下，要优于文献[20]的方法；对于U2R攻击类型的检测，GBDT 模型的检测效果最差，本文方法略优于文献[20]；对于R2L 攻击类型的检测，文献[20]在准确率方面要优于GBDT 模型和本文方法，但是在漏报率方面，本文方法要略好于其他两种模型。

3 结束语

由于现在网络上的攻击数据维度高、噪声大，如果不进行特征的提取，当模型进行学习时，不仅效率和性能低下，而且分类的结果也不是特别理想。本文通过Fisher 方法进行特征的选择，再用PCA 进行特征降维。在不改变数据特征信息的同时，能够有效地减少模型的检测时间。实验表明，通过Fisher和PCA 进行特征提取能够使NDNN 深度神经网络模型在提高准确率和检测率的同时，大大地降低误报率。与其他一些模型相比，本文模型在误报率上有明显的优势。但是，此方法可能不是最好的提取特征的方法，NDNN 神经网络模型的性能也存在着进一步提升的空间,而要更加充分学习数据特征之间的关系。在后续工作中，可进一步研究更好的特征提取方法，与分类模型有效地融合，并改进模型的优化算法，将此入侵检测算法应用于实际的网络中进行实验并不断改进。