基于偏序集的PROMETHEE方法优化研究
2020-10-23岳立柱王国辉
张 飞,岳立柱,王国辉
(1.辽宁工程技术大学 公共管理与法学院,辽宁 阜新 123000; 2.辽宁工程技术大学 工商管理学院,辽宁 葫芦岛 125105;3.辽宁省重要技术创新与研发基地建设工程中心,辽宁 沈阳 110000)
0 引言
PROMETHEE法是最受欢迎的多准则决策方法之一。Brans在1982年首次提出PROMETHEE法,由于在概念和应用上均简便易行,PROMETHEE被广泛应用于处理国防需求[1]、环境管理[2]、化学[3]、物流与运输[4]、企业管理[5,6]等各领域问题的决策中。随着应用领域的扩展,PROMETHEE法逐渐由单一方法发展为方法族。PROMETHEE方法族最初包括部分排序的PROMETHEE I和完全排序的PROMETHEE II,后来又发展出多个版本:如基于区间估计的PROMETHEE III、对连续方案集进行排序的PROMETHEE IV、解决部分约束问题的PROMETHEE V、人脑表示的PROMETHEE VI、用于群决策的PROMETHEE GDSS、用图形表示的视觉交互模块GAIA,以及处理分类问题的PROMETHEE TRI和用于名义分类的PROMETHEE CLUSTER等。在实践应用中,准则权重是PROMETHEE方法不可缺少的先验信息,其强烈地影响着PROMETHEE方法族的应用效果和决策质量。一些学者采用的赋权方式存在误区,使得该模型应用不当,增加了决策风险。因此,亟需研究赋权问题,避免应用错误,提升该模型的应用质量。
当前,与PROMETHEE模型相结合使用的赋权方法,可归结为主观赋权法、客观赋权法和组合赋权法三种类型,不过后两种类型并不适用。主观赋权法是决策者根据自己的偏好和经验给出准则权重信息的方法,如Dephi法[7]、层次分析法[8]。该方法能较好地反映准则的相对重要性程度,有效提取决策情境信息。但该方法主观性过强,精确性不够。为了克服赋权过于主观问题,有学者提出客观赋权法,如熵权法[9]、离差法[10]等。但客观赋权法得到的“权重”无法体现属性自身的重要性,只是该属性在决策方案排序上的作用大小,且“权重”值会随数据变化而变化,稳定性和可继承性较差[11]。组合赋权法是在综合主、客观赋权法基础上提出的,受客观赋权法无法得到真正“权重”的限制,组合权重也无法有效反映指标重要性差异。因此,在三种赋权类型中,主观赋权法恰恰是一种更为合适赋权方法。主观赋权法易于把握研究对象质性信息,例如指标重要性排序,但一般不易给出精确的量化信息;即使能够给出精确权重,在方法论层面也存在挑战。事件的随机性和信息的不完备性导致现实中任何精确权重数值的给出都过于主观武断[12]。应用PROMETHEE家族中的任何一个模型进行决策时需要精确权重,没有具体权重,模型便无法应用。如何解决权重本质上具有的不确定性和模型需要精确权重的矛盾?
偏序集是一个非常有吸引力的决策支持工具[13],不仅可自身独立分析,更可以与其它模型进行结合,进而增强后者的应用范围与鲁棒性。偏序集方法表明,对于含有权重参数的模型,若获取指标权重的定性排序信息,便可以借助偏序集方法运行该模型。岳立柱等[14]在仅知权重顺序信息的基础上,应用偏序集方法表示TOPSIS模型。通过偏序集方法,在仅获取属性序数性质基础上即可完成方案的排序[15],结果不仅具有客观性和保序性[16],而且能够进行类别比较。因此本文在借鉴现有研究的基础上,选择PROMETHEE家族中应用最为广泛的成员PROMETHEE II,应用偏序集方法解决其赋权难题(没有特殊说明,以下PROMETHEE均指PROMETHEE II)。
1 PROMETHEE决策方法
PROMETHEE法是基于偏好指数的一种多准则决策方法。在构建偏好函数基础上,结合特定评估尺度计算偏好指数并确立方案间的优势关系。优势关系以流量形式表示,通过比较方案的净流来对进行排序,净流最大的方案为最优方案。
1.1 偏好函数的确定
令M={1,2,3,…,m},N={1,2,3,…,n},A={ai|i∈M}表示方案集,C={cj|j∈M}表示准则集,函数fj(j∈N)为方案在属性cj上的测度值。对于∀al,ak∈A,dj(al,ak)为方案ai和方案ak在属性cj上的属性值之差,即dj(al,ak)=fj(al)-fj(ak)。构建偏好函数Pj(al,ak),表示在属性cj上al优先于ak的程度。即:
F(d)为al相对于ak的优先程度值。Brans等人[17]给出函数F(d)的六种常用评估尺度类型,包括通用类型、类似类型、线性偏好类型、水平类型、线性偏好及无差异区类型和高斯类型,这些类型基本包括了发生在实际应用中的大部分状况。其取值范围介于0到1之间。一般Pj(al,ak)∈[0,1],Pj(al,ak)的值越趋近于1,表示方案al在属性cj上越优于方案ak。偏好函数也可表示为:
1.2 偏好指数的计算
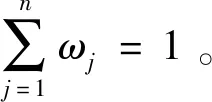
(1)

1.3 优序关系的流量表示
方案之间的优序关系以流量来进行表示,包括流出、流入和净流三种形式。流出即某一方案优于其他方案之和,用Φ+来表示;流入为其他方案优于某一方案之和,用Φ-来表示;净流量是方案流出和流入的差值,用Φ来表示。对于∀al∈A,其流入、流出和净流分别表示如下:
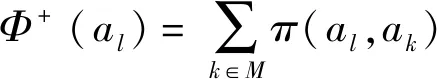
Φ(al)Φ+(al)-Φ-(al)
(2)
PROMETHEE根据Φ(al)的大小对方案进行排序,取值越大表示方案越优。
2 PROMETHEE方法的偏序集表示
2.1 偏序集基础知识
定义2.1[19]设R是集合A上的一个二元关系,若满足自反性、反对称性和传递性,则称R为A上的偏序关系,用“≤”来表示,集合A与其上的偏序关系“≤”一起称为偏序集,记作(A,≤)。
若评价集M=(A,IC)存在偏序关系,则对∀al,ak∈A有al≤ak⟺cj(al)≤cj(ak),j=1,2,…,n。
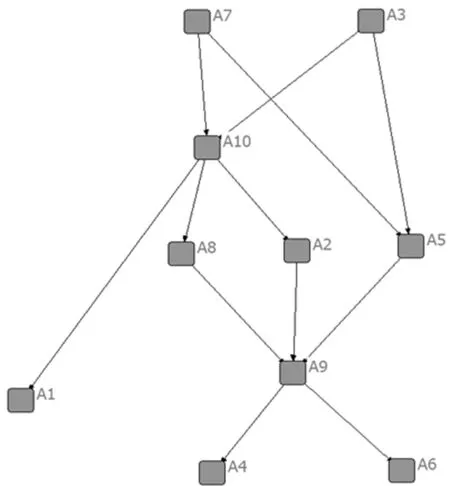
给定偏序集(A,≤),对于∀al,ak∈A,若al≥ak,则记rlk=1,若al (3) 偏序集决策方法根据各方案在偏序集上的hav(al)大小来进行排序。 定理2.1可用如下等价矩阵形式表示: 其中,E为上三角阵,若在矩阵G中,第l行之和大于第k行之和,则Φ+(al)≥Φ+(ak)。 在Brans等给出的函数F(d)的六种常用偏好函数基础上得到的方案流出与流入值之和往往等于或者接近于一个常数。例如,当F(d)使用常用类型,即Usual Criterion时,F(al,ak)∈{0,1},此时Φ+(al)+Φ-(al)=m-1。为了表示的一般性,令Φ+(al)+Φ-(al)=θ,θ∈R。 定义2.2[22]给定一个偏序集P,可以如下构造出与P对偶的偏序集P′:P′与P具有完全相同的元素,只是P′上的序关系与P上的序关系相反:a≤b在P′上成立当且仅当b≤a在P上成立。若P是有限的,则简单地将P的序图倒置便得到P′序图。 定理2.2若Φ+(al)+Φ-(al)=θ,则偏序集(A,M+≤)与(A,M-,≤)是对偶偏序集。 证明设M+的第l行为Φ+(al),第k行为Φ+(ak),M-的第l行为Φ-(al),第k行为Φ-(ak)。 由于Φ+(al)+Φ-(al)=θ,所以Φ+(al)=θ-Φ-(al)。 若Φ+(al)≥Φ+(ak),即知θ-Φ-(al)≥θ-Φ-(ak),所以Φ-(ak)≥Φ-(al)。 根据定义2.2,偏序集(A,M+,≤)与(A,M-,≤)是对偶偏序集。证毕。 由对偶偏序集定义2.2可知,方案的流出序图与流入序图一定是互为倒置的,只需获得流出或流入偏序集中的任意一个,即可得到流出和流入两个互为倒置的方案关系排序图。 定理2.3对∀al∈A,若Φ+(al)+Φ-(al)=θ,当矩阵G=M+-E的第l行大于第k行,E为上三角阵,则al优于ak。 证明由于al优于ak⟺Φ(al)≥Φ(ak),若Φ(al)≥Φ(ak)成立,则定理成立。 由于矩阵G=M+-E的第l行大于第k行,于是Φ+(al)≥Φ+(ak)。根据定理2.2,Φ-(al)≤Φ-(ak)。 又Φ(al)=Φ+(al)-Φ-(al),于是Φ(al)-Φ(ak)≥0,即Φ(al)≥Φ(ak),证毕。 根据定理2.3可知,当方案的流入和流出之和为常数时,方案集A中方案的净流(Φ)排序与流出(Φ+)排序一致,与流入(Φ-)排序相反。在常见的六种类型偏好表达式中,常用类型和类似类型的方案流出与流入值之和等于常数m-1,其余类型接近于这个常数。因此,PROMETHEE模型所采用的基于净流的排序方式存在信息冗余,只需单独获取流入或流出矩阵,即可完成所有方案排序。 设评价集M=(A,IC)对于∀al,ak∈A,若Φ+(al)≥Φ+(ak),则称al≥ak。根据方案间的比较关系可得比较关系矩阵R。为进一步简化关系数量,可将关系矩阵转化为HASSE矩阵,进而通过HASSE图来表示方案间的偏序关系。文[23]给出了比较关系矩阵与HASSE矩阵之间的转化关系: HR=(R-I)-(R-I)2 (4) 其中,R代表比较关系矩阵,HR代表HASSE矩阵,I为单位阵,矩阵(R-I)2为布尔代数。 综上所述,应用偏序集表示权重未知的PROMETHEE模型的排序步骤如下: 第二步:按权重大小对指标进行重新排序和编号,使第j个指标权重为第j大; 第三步:根据定理2.1,分别得到流出、流入和净流的比较关系矩阵R+、R-、R。 第四步:通过式(4)将方案比较关系矩阵转换为HASSE矩阵,并绘制HASSE图对排序结果进行分析。 利用文献[24]中的实例,验证偏序集排序的有效性。该实例包含10个备选方案,方案集A={A1,A2,…,A10},包含5个评价准则,均为效益型准则,准则集为IC={c1,c2, …,c5},权重向量为W={ω1,ω2,…,ω5},偏好函数选择通用类型,具体数据见表1。算例中虽然给出具体权重值,本文仅提取权重顺序,即ω2>ω1>ω4>ω3>ω5>0,通过该序数对方案进行排序分析。 表1 方案原始数据表 表2 方案在不同指标上的流出、流入及净流量表 其次,根据算例中所给出的权重顺序,即ω2>ω1>ω4>ω3>ω5>0对准则进行重新排列,根据定理2.1对不同指标上方案的流出、流入和净流进行两两比较,分别得到流出、流入和净流的关系矩阵R+、R-和R,见表3~表5。 表3 关于流出的方案比较关系矩阵 表4 关于流入的方案比较关系矩阵 表5 关于净流量的方案比较关系矩阵 最后,依公式(4),由方案比较关系矩阵得到HASSE矩阵,并绘制HASSE图,如图1~图3所示。 由图1~图3可见,无论是基于流出、流入还是净流的方案关系HASSE图都包括四个层集:其中,方案A4和A6属于同一层集,方案A3和A7同一层集,方案A1、A2、A5、A8和A9同一层集,方案A10一个层集。层集之间的比较关系为{A4,A6}≻{A1,A2,A5,A8,A9}≻{A10}≻{A3,A7}。 图1 基于流出的方案关系HASSE图 图2 基于流入的方案关系HASSE图 图3 基于净流量的方案关系HASSE图 对比分析: 本文方法的排序结果为{A4,A6}≻{A1,A2,A6,A8,A9}≻{A10}≻{A3,A7},是一种偏序结构。文[24]给出的结果为全序结构A4≻A6≻A9≻A2≻A8≻A5≻A1≻A10≻A3≻A7。为进一步与文[24]进行对比分析,利用式(3)计算方案在(A,≤)上的高度值,展开更细致的方案排序,结果为:hav(A1)=8.8,hav(A2)=5.5,hav(A3)=1.1,hav(A4)=9.7778,hav(A5)=4.7143,hav(A6)=9.7778,hav(A7)=1.1,hav(A8)=5.5,hav(A9)=7.7,hav(A10)=3.3,于是可得A4=A6≻A1≻A9≻A2=A8≻A5≻A10≻A3=A7。由此可见,本文方法与文[24]方法的排序结果非常相似。但是本文方法有如下不同之处: (1)本文方法在操作中更为简便。文[24]方法采用精确权重参与计算,却没有明确给出权重来源。本文方法充分考虑权重赋值困难且充满争议的特点,仅使用权重顺序即完成方案排序。权重顺序在实际决策中易于获取,大大降低了应用的难度。应用本文方法免去了仿真的麻烦,并且可以对结果进行解析分析。 (2)本文方法的理论框架更为稳健。文[24]方法将一组具体的权重向量引入到PROMETHEE模型中影响决策,本文方法则是将权重空间引入PROMETHEE模型,充分考虑权重赋值变化的可能。只要满足权重顺序不变,评价结果就不变,因而本文的方法稳健性更强。 (3)本文方法可对评价结果进行结构化分析。文[24]给出的是方案的线性序,仅反映方案优劣关系。本文方法给出的结果是同时包含可比关系和不可比关系的偏序结构。实际决策中,偏序集排序更接近决策本质。它不仅能够进行方案排序,且能够对方案进行分层、归类。一方面排序结果中的可比关系凸显排序结果的稳定性;只要权重顺序保持不变,方案间可比关系就不会发生改变;另一方面不可比关系体现排序结果的可变性;随着权重的变化,方案排序在一定概率条件下会发生颠倒。偏序结构提供一个方案的识别框架,这种结构化属性保证了评价结果的稳定性和灵活性。 针对多准则决策方法PROMETHEE在应用中具体权重信息无法获知的情况,提出一种应用偏序集表示的改进方法,应用该方法仅需获取权重序数信息即可进行方案排序。本文方法本质上是通过序关系将权重空间融入到模型当中,取代原方法的单一权重,由此展示了排序结果的稳定性与灵活性。通过算例表明,该排序方法排序稳健、复制容易,且体现定性与定量相结合的特点。尽管本文结果与算例中排序结果基本一致,但本文进一步揭示了排序中稳健方案和易变方案。2.2 用偏序集表示PROMETHEE的流出排序

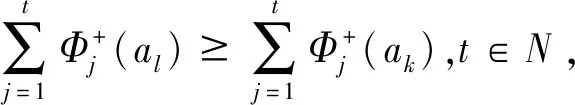

2.3 偏序集表示流出与流入的关系
2.4 偏序集表示净流排序
2.5 方案的关系矩阵生成与HASSE矩阵转换
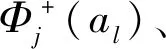
3 算例研究
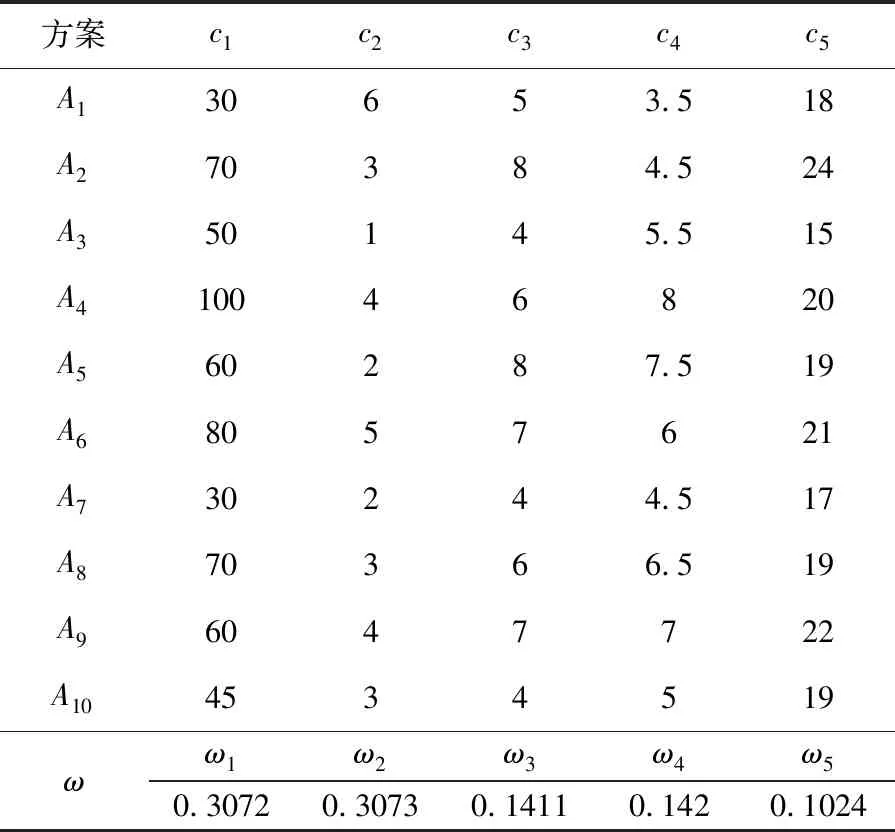
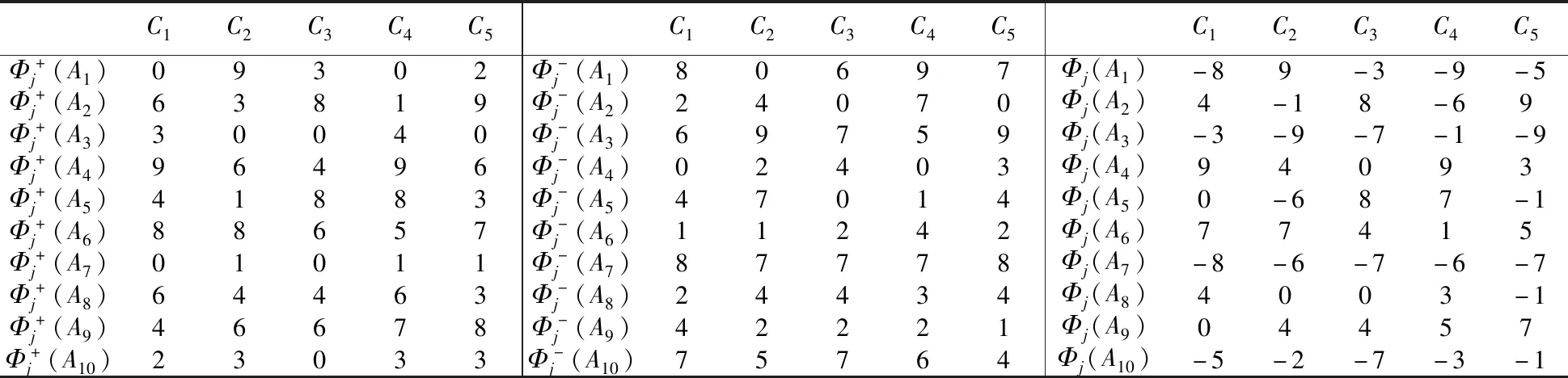


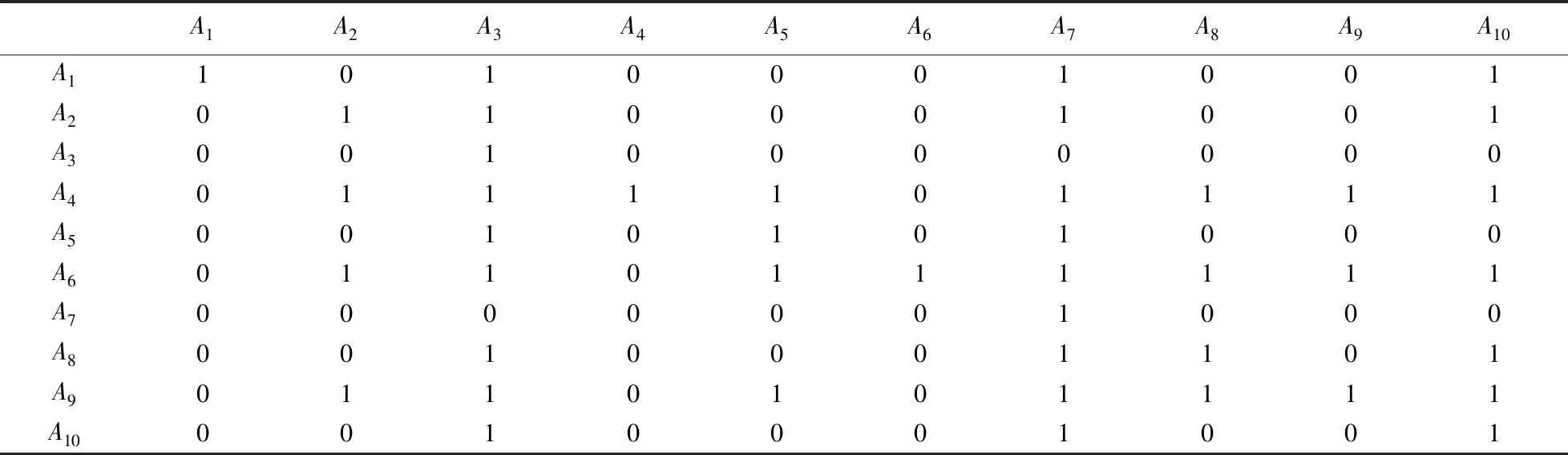
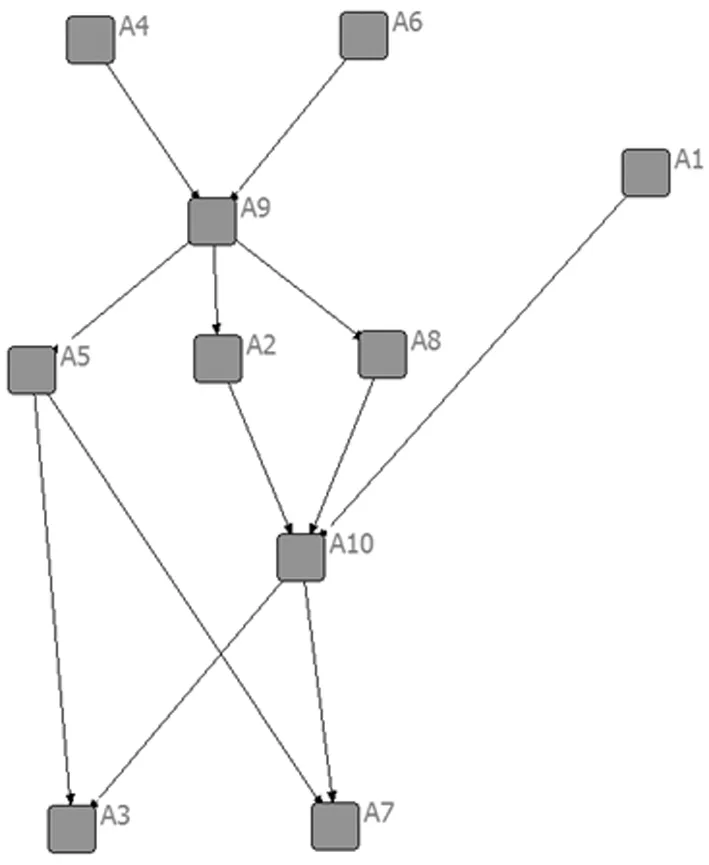

4 结论
