波形钢腹板组合箱梁竖向剪应力算法研究

2020-10-23钱淼

交通科技 2020年5期

钱淼

(中铁大桥勘测设计院集团有限公司武汉 430050)

波形钢腹板组合箱梁桥充分利用混凝土承压、钢腹板承剪的特性，自重轻、结构受力明确，是一种经济、合理的桥梁结构[1-3]。目前，国内外学者认为波形钢腹板组合箱梁桥的竖向弯曲剪应力主要由钢腹板承担,且在设计波形钢腹板箱梁桥时，也只考虑钢腹板承受竖向剪力，但实际上混凝土结构也承受一部分竖向剪力[4-6]，精细化设计应该考虑混凝土结构承受部分竖向剪力。目前单箱多室箱梁腹板的竖向剪力分配计算难度大，所以有必要研究波形钢腹板箱梁竖向剪应力计算理论和开发相应的软件。

1 有限元计算算法

将文献[7-9]的计算方法进行改进，使其适用于多材料结构截面的横向剪应力计算，其受力模型，见图1。

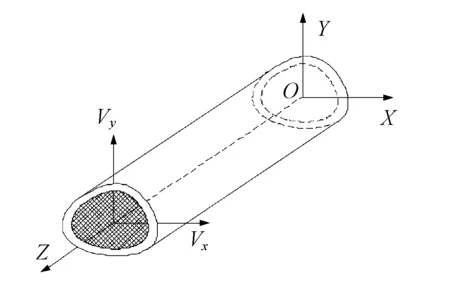
图1 梁横向受力图

悬臂梁，自由端分别受X和Y方向的剪力Vx和Vy作用，采用翘曲函数表示截面的位移。

(1)

(2)

φ(x,y)-a1y-a2x

(3)

式中：u、v和w分别为X、Y、Z方向的位移分量；φ(x，y)为翘曲函数；L为梁单元长度。

(4)

式中：Vx和Vy分别为X和Y方向的剪力；a1、a2、a3、a4为常数，与梁的边界条件相关。

(5)

(6)

(7)

(8)

横向力作用下，杆的总势能为

Ep=U-W

(9)

式中：U为应变能，

(10)

其中：υz为钢材泊松比。

(11)

(12)

W为横向力作用下的外力做功。

(13)

文献[7]、[10]将截面网格划分为等参单元，令等参单元形函数为H(ξ，η)，ξ和η为自然坐标，单元内翘曲函数可以由形函数和节点翘曲函数获得。

(14)

对翘曲函数求导

(15)

利用最小势能原理δEp，由式(9)、式(10)和式(13)得截面在受剪时的平衡方程。

(16)

将式(15)代入(16)，得到梁在受到横向力作用时的平衡方程表达式

Keψi=fs

(17)

式中：ψi为单元节点的翘曲函数值向量，是待求未知量；Ke为单元刚度矩阵；fs为在横向力作用下的广义力向量。根据下式计算

(18)

yCy)]detJdξdη

(19)

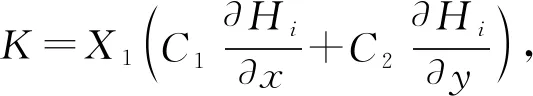
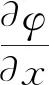
钢腹板竖向剪应力计算公式为

(20)

式中：υz为钢材泊松比；Ez钢材弹性模量；EBi为混凝土与钢材弹性模量比；GBi为混凝土与钢材剪切模量比。Ixx和Iyy为截面在过形心的x和y方向的换算截面惯性矩；Ixy为换算截面惯性积；A为换算截面面积；As为实际截面面积；Az为钢材实际面积；Ai为混凝土实际面积。换算截面是将混凝土换算成钢材。

2 计算实例

实例的波形钢腹板箱形截面见图2，为单箱三室箱形组合截面，顶底板为钢筋混凝土，钢腹板厚16 mm。受竖向剪力1 000 kN作用，求钢腹板剪应力。

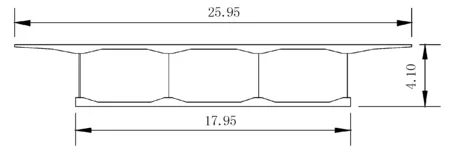
图2 波形钢腹板箱梁截面(单位：m)

2.1 本文算法计算结果

根据本文算法编写的软件计算了顶板悬臂板宽度分别为4.24，1.74和0.24 m的3种截面竖向剪应力分布，边腹板竖向剪应力分别为4.258，4.264，4.250 MPa，中腹板竖向剪应力分别为4.242，4.256，4.266 MPa。根据计算结果顶板悬臂板的宽度越窄边腹板分配的剪力越小，3种截面的边中腹板剪力分配比分别为1.004，1.002，0.996。