二次函数中三角形面积最大值问题解法探究

■湖南省冷水江市城东学校 谢雄俊

二次函数是初中数学知识体系中的重点和难点，它综合几何图形形成的综合题和探究题更是增加了学习的深度和广度，对学生的思维能力和学习能力提出了更高的要求，成了近年来中考的热点。本文将以2016年湖南省某市数学中考第26题为例，就二次函数中三角形面积最大值问题的解题思路、方法与技巧进行探讨和归纳，供大家参考。

例：如图，抛物线y=ax2+bx+c（a，b，c为常数，a≠0）经过点A(-1，0)，B(5，- 6)，C(6，0)。

图1

（1）求抛物线的解析式：(y=x2-5x-6)

如图，在直线AB下方的抛物线上是否存在点P使ΔABP的面积最大？若存在，请求出点P的坐标；若不存在请说明理由。

（3）若点Q为抛物线的对称轴上的一个动点，试指出△QAB为等腰三角形的点Q一共有几个？并请求出其中一个点Q的坐标。

下面着重探究问题（2）“二次函数中三角形面积最大值问题”蕴含的解题思想、方法与技巧。

解法一：割补法

解：过点B作BD⊥x轴，连接PD

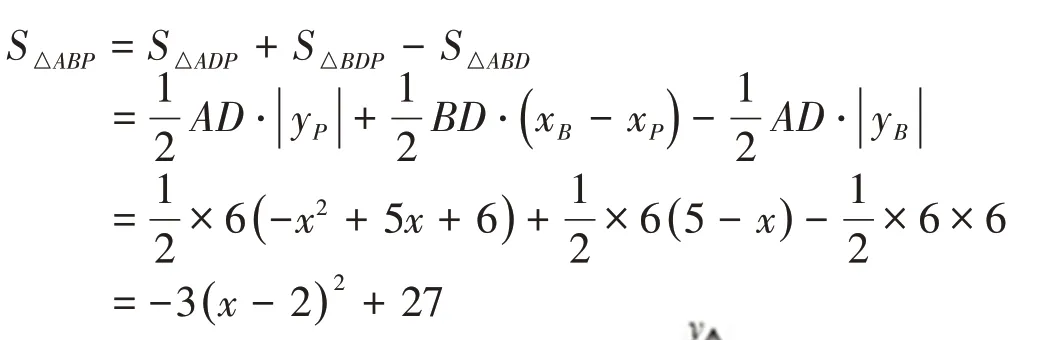
图2

因此当x= 2 时，S△ABP最大值27

评析：割补法通过灵割、巧补化不规则图形为规则图形或化不规则图形为有利于面积表达的常规几何图形进行面积的推导和计算。本题利用割补法求△ABP的面积，关键在于分割出有利用面积表达的△ADP和△BDP，利用其面积和减去△ABD的面积。使用割补法解题时可考虑乘法分配律与结合律，降低运算难度。

解法二：铅锤法

图3

解：过点P作PD⊥x轴于点D，交AB于点E

设P(x，x2- 5x- 6)(-1＜x＜5)，则E(x，-x- 1)

∴PE=(-x- 1)-(x2- 5x- 6)=-x2+ 4x+ 5

因此当x= 2时，S△ABP最大值27

评析：铅锤法是求斜置三角形面积最常用的方法，其利用“横平竖直，改斜归正”大大降低了解题难度。如图：

图4

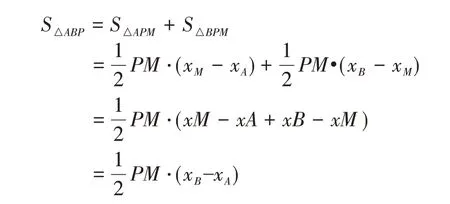
解法三：三角函数法

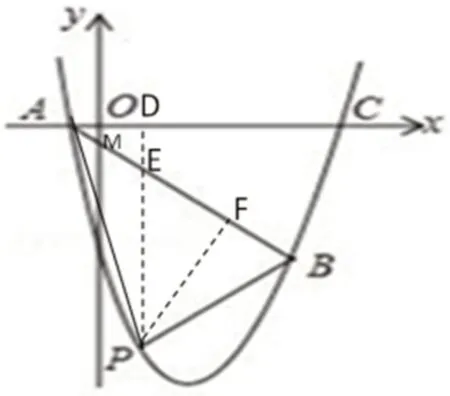
图5

解：过点P作PD⊥x轴于点D，交AB于点E；过点P作PF⊥AB于点F

设P(x，x2- 5x- 6)，则E(x，-x- 1)

∵A(-1，0)，B(5，- 6)

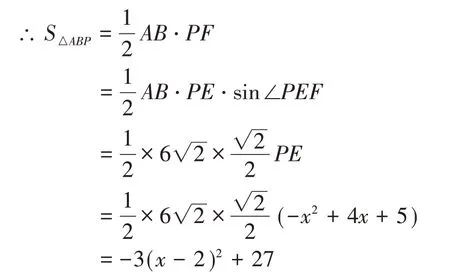
∴当x= 2时，S△ABP最大值27

评析：锐角三角函数建立起了三角形边角之间的关系，为此类问题的解决提供了新的思路和方法。本题因△ABP底AB为定值，求其面积只需用P点横坐标表示PF长即可。借用三角函数性质得则进而求得△ABP面积最大值。

解法四：切线法

解：过点P作直线l∥AB，

设直线l的解析式为y=-x+b

图6

当Δ= 0 时，解得x1=x2= 2，直线l 与抛物线只有一个交点。

∴P(2，- 12)，E(2，- 3)

∴PE=-3-(-12)= 9

∴S△ABP最大值

评析： 切线法从几何模型的角度另辟蹊径解决了二次函数中三角形面积最大值问题。题中因三角形底AB为定值，要求面积最大，只需高PF最大。又因为P是抛物线上一个动点，且在AB下方，可过动点P作直线AB的平行线l逐渐向下平移。移动中发现直线与抛物线交点数从2 个变为1 个时，高PF最大，此时三角形面积最大。本文从各个角度探究了二次函数中三角形面积最大值问题的解法，但在教学中，引领学生探究习题的解法，不只是为了让学生会用不同的方法解题，重要的是启发学生的思维，发展学生的思维，提高学生解决问题的能力。