基于自适应粒子群优化FastSLAM算法的改进

梁雪慧，张瑞杰，赵 菲，程云泽

（天津理工大学电气电子工程学院，天津300384）

无人驾驶车辆最明显的功能之一是建立周围环境的地图并且通过地图进行导航，这通常被称为SLAM（同时定位与建图）[1].然而，在实施SLAM时同时让无人车进行定位和建立地图存在一定的困难，难点在于如果要使无人车知道其真实位置，必须在定位之前构建非常精确的地图[2]；但是在建立精确的地图之前，车辆也同样必须准确对其自身定位，否则会导致误差的不断累积从而很大程度上影响结果的精确性.车辆在行驶过程中的任何摩擦，控制损失或者小障碍都往往是导致错误测距的原因，从而对真实位置的估计不良[3-4].

针对SLAM[5-6]存在的上述问题，Montemerlo等最早提出了FastSLAM算法，采用粒子滤波（particle filtering，PF）的方法，把SLAM分解为两个“独立”的问题，并分别采用不同的滤波方式使之能够在大规模复杂的环境中运用.但是在计算过程中，随着粒子种群不断更新权值，这其中有大部分的粒子权重会非常小，甚至权重会集中在种群中的几个甚至单一粒子上，最终会出现“粒子退化”的问题.为了解决这些问题，许多学者提出了诸多改进的算法.文献[7]中提出了用粒子群优化来代替粒子滤波的重采样过程，虽然改善了在求解复杂的非线性函数优化问题时状态估计的精度，但是粒子群优化算法本身容易发生粒子种群早熟收敛的现象.文献[8]中，提出了基于遗传算法的FastSLAM2.0算法，虽然一定程度上解决了粒子退化的问题，使得参与计算的大权值粒子数目有所提高，但由于FastSLAM2.0算法和遗传算法本身计算的复杂性，算法的实时性上有所欠缺.文献[9]中利用免疫学的原理理论，结合了人工免疫算法，把目标模版的特征点看作抗原，利用变异的方式淘汰对抗原亲和力小的抗体，由此让结果更快速的接近最准确，但这个算法复杂、耗时且利用率较低.

综合这些算法目前存在的问题，本文提出一种基于自适应粒子群优化算法的FastSLAM算法.先利用粒子的后验位姿提议分布构建粒子的筛选区间[10]，区间内的粒子得以生存，同时使区间外的粒子向高似然概率区间移动，改善算法初期粒子的分布，然后通过自适应粒子群优化算法来更新粒子的全局最优位置以及粒子历史最优，提高粒子的优越性，进一步通过交叉变异操作步骤，克服了原始粒子群算法容易出现的“局部最优”问题.最后，将改进后的算法应用于无人驾驶车辆的FastSLAM，并进行仿真结果验证.

1 无人车FastSLAM的算法模型

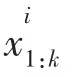
FastSLAM所示的误差会随着时间的推移而累积[12]，因此产生了广泛存在的权值集中在少数粒子的问题.粒子退化问题意味着计算效率在大部分对于计算结果仅有微小作用的粒子影响下会不断降低，且由于误差的累积而导致结果精度也受到影响.通过计算粒子种群中的有效粒子数Neff，Neff的值越小则说明粒子退化现象越严重，Neff可由式（1）近似计算：

式（1）中，ωi为第i个粒子的权重值；k是当即时刻.如果通过判定得出参与到后续计算的粒子数目小于有效粒子数（一般情况下，有效粒子数=0.8×粒子总数），就对不同权重的粒子进行重新采样，使权重大的粒子的数量增多.通过重采样步骤，虽然可以一定程度上减弱粒子的退化现象，但是每一个粒子所包含的位姿信息是所有时刻的位姿信息，然而，算法每一次的迭代过程只需要当即时刻的位姿信息，进行重新采样之后，虽然淘汰了大多数权重小的粒子，但同时也删除了这些粒子中所包含的过去时刻的信息，并且，权重大的粒子被多次复制，那么复制出的粒子也许都继承的同一个原始粒子的信息，这样虽然保证了一定数量权值大的粒子参与计算但是大量的粒子位姿信息被淘汰，从而会大大削弱地图估计的精确性，引起粒子缺乏多样性的问题.

2 基于自适应粒子群优化算法的FastSLAM算法

传统的FastSLAM算法中由于需要对粒子进行重采样，会导致种群中只有少数几个粒子甚至单一高权重粒子参与到后续计算中[13-14]，为了改善粒子集的多样性，同时避免粒子群优化算法中容易出现的局部最优现象，引入自适应粒子群优化算法来优化粒子集.

粒子群优化算法[15]容易出现的局部最优（也称为早熟收敛）问题是指计算过程中粒子种群进化迭代到一个不是全局最优状态，但是粒子群的进一步迭代已不可能产生更好的可行解，反映在粒子适应度值上就表示为：已获得的当前最优粒子的适应度值小于解决方案的最优值且适应度值不再更新.自适应粒子群优化算法[16]是一种基于生物群体智能且加入了交叉变异的自适应策略的全局优化方法，在多目标优化、动态系统的跟踪和优化以及模糊分类等方面都发挥了重要的作用.而在算法初期采用筛选粒子[12]的方式使得粒子分布更为合理，再用自适应粒子群的优化过程代替粒子重采样过程，这样既克服了粒子滤波算法带来的粒子贫乏和粒子多样性减弱等问题，又克服了普通粒子群优化算法中粒子群的早熟收敛问题.本文将这两种方法结合并引入FastSLAM算法中，在保证计算效率和结果精度的前提下得到更加优秀的粒子集.

2.1 自适应粒子群优化算法

本文采用的自适应策略为：交叉变异操作[16-17].根据算法的收敛情况自适应的确定进行交叉变异操作的概率，并且根据每个粒子与全局最优粒子的欧氏距离，将交叉算子引入群体中高度聚集的粒子，然后引入变异算子以增强全局最优粒子的局部搜索，并用备份好的原全局最优粒子替换掉当前种群的适应度最差的粒子.

在改进后的算法中，用粒子的适应度值的大小来衡量粒子的位置，适应度越高，粒子的位置就越优秀，粒子与现实的匹配度就越高，可以看出此时适应度与传统FastSLAM算法中权值的定义是一样的，因此用式（2）来定义粒子的适应度为粒子权重：

对于每个粒子个体用一维向量X表示其空间位置，用速度向量V来表示粒子在空间中的移动方向和距离.种群中第i个粒子在第t次迭代时，粒子的位置向量可以表示为式（3）：

速度向量可以表示为式（4）：

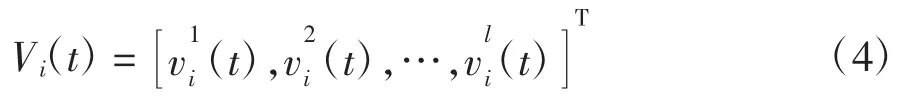
截止到第t代，粒子i搜索到的最优位置记为

称为局部历史最优位置，记为Pbest（t）.群体中所有粒子经历过的全局最优位置记为Gbest（t），Gbest（t）可以通过公式（6）计算得到.

在计算过程中，粒子群一旦陷入局部最优，往往很难自拔，从演化计算中陷入局部最优时变异策略的经验学习到：通过计算自适应的概率来引进交叉变异操作，自适应的概率定义为：

式（7）中，μ和σ是变异率的调节参数，在日常操作中μ设置为0.001，σ设置为0.005.Re是当最优值不再更新或者更新不明显时开始计次的迭代数.若最优值不断更新，则不对种群进行自适应优化操作；如种群收敛速度停滞，连续若干代不更新或者最优值更新不明显，Re将累积增大，对种群进行交叉变异操作的概率也随之加大.具体调节措施如下：

首先，复制种群中的最优粒子，然后将种群中出最优之外的每个粒子依次取出，判断依次取出的粒子与最优粒子的变量空间距离是否小于计算得出的阈值，如果小于阈值，则依据公式（10）交叉两个粒子.

两个粒子的变量空间距离用欧几里得距离来定义：

式（8）中，l为粒子的变量空间距离；D为搜索区域的面积，x1和x2是种群中进行对比的两个粒子.阈值定义为：

式（9）中，t代表当代迭代次数，T表示最大迭代次数；ub和lb表示搜索区域的上下限；n是调节参数.由式（9）得出，可以根据种群进化的过程对阈值进行调整.算法初期，由于种群中粒子具有多样性，此时不宜对种群进行调整（阈值设置较大）；随着t的不断增加，种群中粒子逐渐向最优粒子靠近，粒子的多样性逐渐减弱，就可能出现粒子种群的早熟收敛，此时需要对种群进行必要的自适应优化策略，更新粒子群的状态.

具体交叉操作按照式（10）进行：

式（10）中，cx1和cx2是交叉操作生成的新粒子；x1和x2是父粒子；e是一个（0，1）区间的D维随机数列.

进行交叉操作后，更新粒子的权重（即适应度）.如父粒子的适应度增加，则用更新后的粒子来代替父粒子；如适应值恶化或者不变化，则下一步的变异操作，变异后舍弃不够优秀（适应度低）的粒子，用两个粒子中相对适应值较高的粒子来代替，具体变异操作如下：

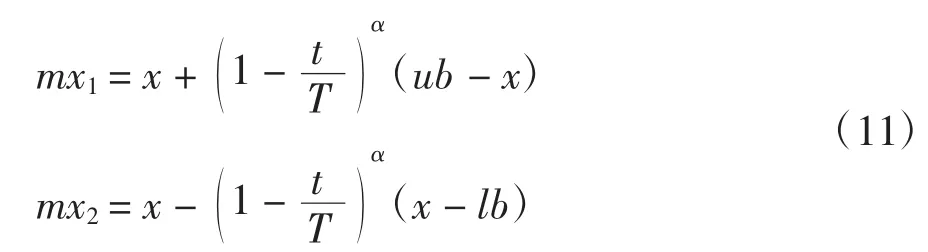
式（11）中，mx1和mx2是经过变异操作的粒子，其余参数含义同上，然后加强全局最优粒子局部细搜索.具体操作是在沿着搜索区域的上下限方向移动全局最优粒子一个很小的步长，以获得一组新的粒子，更新这组粒子的适应度，并舍弃适应度低的粒子，用适应值更佳的粒子来代替.最后整个种群中具有最小适应度的粒子被一开始复制的原始最优粒子替换.

2.2 自适应粒子群优化算法实现步骤

图1所示为自适应粒子群优化算法的具体步骤，在算法执行交叉变异操作之后，更新粒子的适应度，用备份的原全局最优粒子替换适应值最差的粒子；再按照标准的粒子群算法更新种群中每个粒子的速度和位置，更新全局最优粒子Gbest和粒子历史最优Pbest，从而得出最优的粒子群.

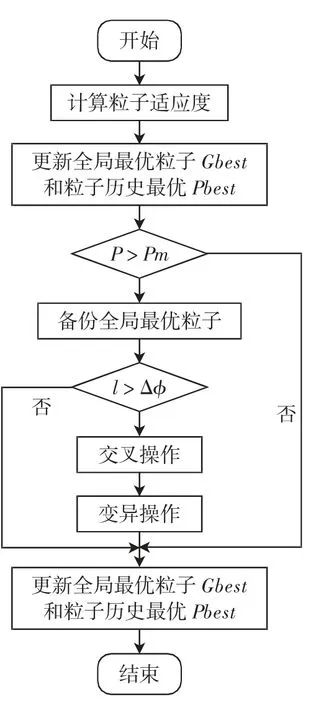
图1 自适应粒子群优化算法流程Fig.1 Self-adapt swarm optimization algorithm flow

2.3 自适应粒子群优化FastSLAM算法的实现过程

在传统FastSLAM算法的基础上做了两处改进：一是用自适应粒子群优化过程代替粒子滤波中的重采样，另一处改进是通过设置筛选区间，区间内的粒子得以生存并且区间外的粒子向中心区域移动，从而改善粒子在算法初期的分布.

详细实现过程如下：

步骤1：计算各个粒子的后验位姿建议分布.

步骤2：从建议分布中采样

式（12）中，xk为粒子在k时刻的采样位姿；xk-1为k-1时刻粒子的采样位姿；zk为k时刻的观测信号；uk为k时刻的控制信号，i取1到N.

步骤3：计算各个粒子的适应度

步骤4：计算粒子的筛选区间，并对区间外的粒子进行移动筛选区间：

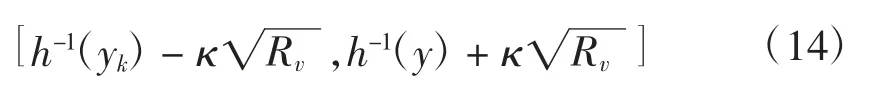
式（14）中κ为区间调节系数，假设噪声服从高斯分布；Rv即是高斯噪声的方差；h-1（yk）为粒子位姿提议分布的期望。区间内的粒子得以生存，对区间外的粒子沿期望方向移动，且移动方法如下：

步骤5：更新全局最优粒子和粒子历史最优.

步骤6：备份全局最优粒子，对种群进行操作.

步骤7：粒子优化.

步骤8：地图估计与更新.

3 仿真结果及实验分析

3.1 仿真模型

无人车的里程计数学模型如下：

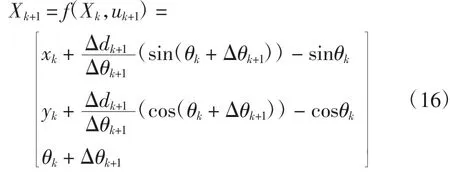
式（16）中，Xk+1表示无人车k+1时刻的位姿状态；uk+1表示无人车在k+1时刻里程计的控制输入；θk为k时刻的无人车转过的航向角且其值的范围位于[-180°，+180°]之间；D表示两驱动轴的间距.观测模型为：

式（17）中，r和θ分别表示检测到的环境特征与无人车之间的距离和运动航向角；xi和yi表示观测到的第i个路标位置；ωk表示观测噪声.

3.2 仿真结果分析

为了验证基于自适应粒子群优化的FastSLAM算法的实际有效性，本文在MATLAB仿真平台上通过独立实验分别对三种不同的算法进行仿真对比分析.

创建了如图1所示一个基于路标点和导航点的仿真环境，环境中设置28个路标，30个导航点.无人车的相关参数：两驱动轮之间间距D=2.7 m；运动速度为0.5 m/s；航向角速度6 rad/s；传感器采样时间ΔT=0.025 s，运动过程噪声0.3 m/s；仿真过程中取20个粒子.

运行结果如图2，其中，“*”为导航点，“○”为路标.

图2 仿真环境Fig.2 Simulation environment

为了验证算法的优越性，采用一个样本空间，粒子总数都为40，对比了传统FastSLAM算法，基于二阶差分粒子滤波的FastSLAM算法以及基于自适应粒子群优化FastSLAM算法进行仿真.

由图3可知，基于自适应粒子群优化算法的FastSLAM算法的无人车实际运行路径与预设路径相比，偏差随着时间的推移有所波动，但整体路径偏差要比其他两种算法低，这表明自适应粒子群优化算法的确对于估计精度有一定提高，因此验证了基于自适应粒子群优化改进后的FastSLAM算法在无人车运行中的精确性.

图3 算法运动偏差对比Fig.3 Simulation environment

为了满足无人车运行的实时性要求，基于三种算法的估计方根误差和运行时间两个指标进行了仿真实验的对比，结果如表1，结果表明，改进后的FastSLAM算法不仅在运算效率方面表现优异，并且有效的提高了算法的估计精度，完全可以满足无人车实时性的要求.

表1 估计方根误差和算法运行时间表Tab.1 Estimated square root error and algorithm runtime table

4 结论

在传统的FastSLAM算法中，对粒子集进行重采样会引起“粒子耗尽”问题，而单一的粒子群优化算法会随着不断迭代而容易发生“局部最优”的情况，针对这两种算法的特点，设计了一种改进的FastSLAM算法，用自适应粒子群优化来代替重粒子滤波，并且在算法初期通过构建区间来筛选粒子，使得粒子的分布更加合理.种群中的粒子有较多机会参与到后续的运算中，而不是仅仅被丢弃.另一方面，许多优秀的粒子所包含的信息传递给了新粒子，而且交叉变异操作的进行，又保证了粒子种群的多样性.理论分析和实验表明，基于自适应粒子群优化的FastSLAM算法在估计精度和计算效率方面的性能都较为突出，满足了无人车实时并且精准运行的要求.