基于ADRC的微型直流电机柔性伺服控制系统研究

贺睿杰，刘 畅

（天津理工大学电气电子工程学院天津市先进机电系统设计与智能控制重点实验室，机电工程国家级实验教学示范中心，天津300384）

对于服务机器人，在很多场合都需要灵活的机械手，不仅需要其能够实现精确的位置控制、良好的动态性能、还需要其有良好的环境适应能力[1-2]，以及一定的柔性，即根据不同物体所能承的受力，对物体与机械手之间的接触力进行精确的控制，从而在不损坏物体的前提下完成抓取动作[3].用于机械手控制的电机有多种，如舵机、伺服电机、步进电机、直流电机等，对于舵机和伺服电机来说，其集成了位置控制环，但是缺少柔性控制容易造成机械手或者被抓取物体的损坏，步进电机同样可以实现开环的位置和速度控制，但是在一些极限的情况会出现丢转的现象并且还会造成控制不是很精确的情况，且动态性能一般[4-5].直流电机相对容易控制，且具有体积小成本低等特点，设计合理的控制系统还能提高控制性能，非常适合用于服务型机器人的机械手驱动系统当中.因此在未来的服务机器人中，基于微型直流电机的柔性伺服控制系统需求量将会非常大.

国内目前具有机械手功能的服务机器人仍然处于实验室阶段，各项的性能需要提高，尤其是需要从服务机器人场景出发，满足如下要求：

1）具有良好的自适应性和良好的抗干扰性

一个服务型机器人，短时间内的作业种类会有很大的不同，有可能抓取形状不规则的物体，有可能抓取质量较大的物体，也有可能抓取容易变形的物体，同时面临着其它原因引起的负载突然变化的情况，这就需要具有良好的适应性和抗干扰性.

2）具有柔性抓取的特性

由于机器人抓取的对象是未知的，有可能抓取质地脆、易损坏的物体，这就需要机械手抓取物体时对抓取力进行一定的控制，使其具有一定的柔性，而不只是速度和位置的控制，只有这样才能够真正的应用到服务机器人上.

1 直流电机数学模型建立

直流电机结构如图1所示.接入直流电源以后，电刷A为正极性，电刷B为负极性.电流从正电刷A经线圈ab→cd，到负电刷B流出.电流总是由电刷A经N极下的导体流入，再沿S极下的导体经电刷B流出[6].因而电磁力和电磁转矩的方向始终保持不变，使电机能沿逆时针方向连续转动.

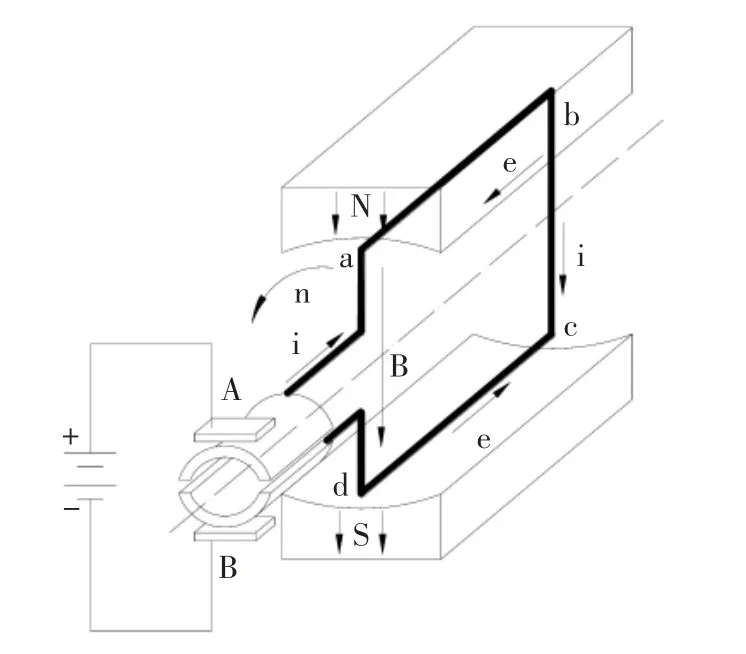
图1 直流电机结构图Fig.1 Structure diagram of DC motor

额定励磁下的负载转矩和电磁转矩，以及转速与反电动势之间的关系分别为：

式中，Td为负载转矩；Te为电磁转矩；Cm为电动机额定励磁下的转矩系数，Km为转矩常数，Φ为磁通；Id为等效负载电流；Ia为电枢回路电流；Ea为反电动势；Ce为电动机额定励磁下的电动势常数，Ce=KeΦ，Ke为电动势常数；n为电机转速.

根据牛顿定律可得：

其中，J是转动惯量；ω是电机转速.

其中，ρ为转动部分的惯性半径；D为转动部分的惯性直径；g为重力加速度（9.81 m/s2）；m为旋转部分的质量；为旋转部分的重量.将式（1）（2）代入式（7）可得：电机电枢回路机电时间常数为：

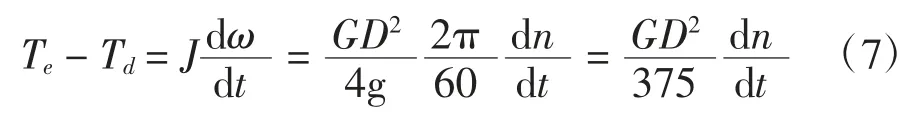
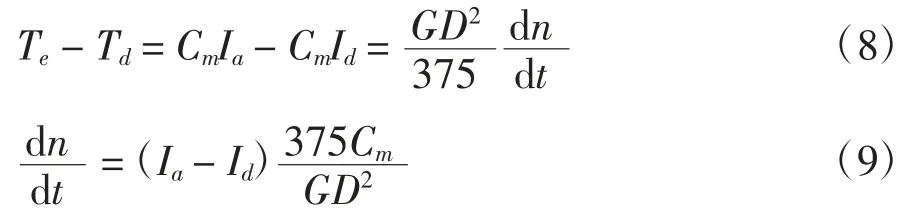
将（9）与式（10）结合可得：根据基尔霍夫电压定律，电枢回路电压满足：

综合式（12）和（3）可得：

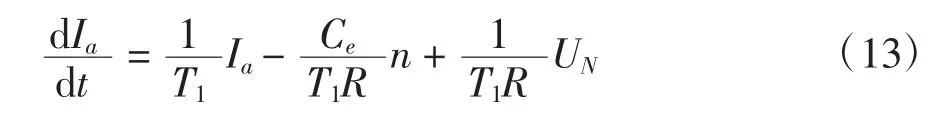
其中电磁时间常数为：

联合（11）和（13）可得出直流电机最终模型如下：

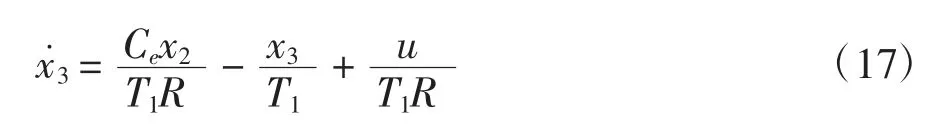
其中，x1为电机转子位置，单位为脉冲个数.本仿真中电机每转有240个脉冲；x2为电机转子角速度；x3电机电枢电流；R为电机转子电阻.系统参数如表1所示.

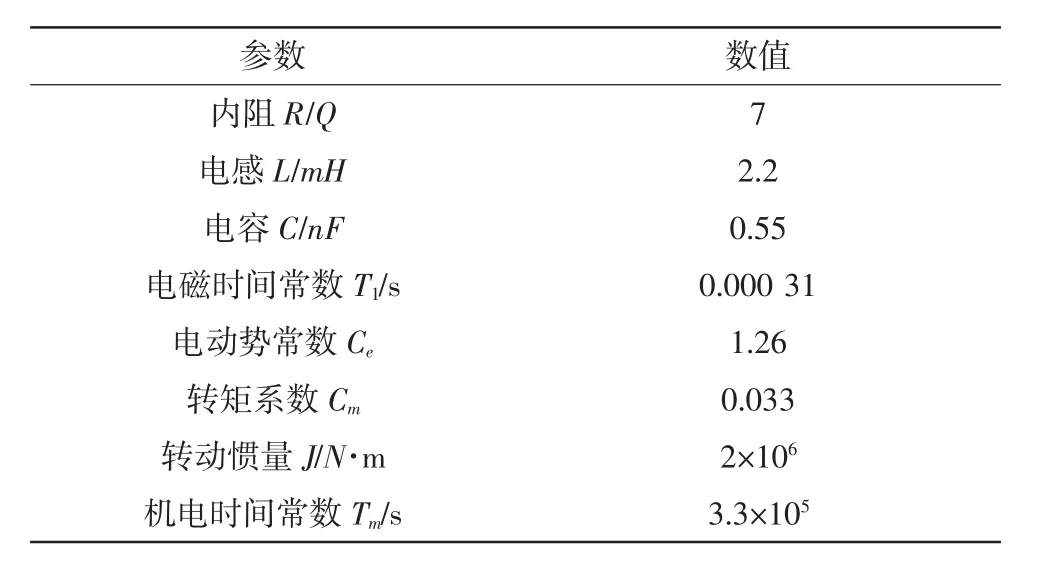
表1 系统参数表Tab.1 System parameter table

2 控制系统算法研究与实现

2.1 自抗扰控制器设计

自抗扰控制算法（ADRC）算法由跟踪微分器（Tracking Differentiator，TD）、非线性状态误差反馈律（Nonlinear State Error Feedback，NLSEF）以及扩张状态观测器（Extended State Observer，ESO）三大部分构成[7].

TD根据给定值v安排过度过程v1，并提取其微分信号v2；离散型最速TD可表示成下式：

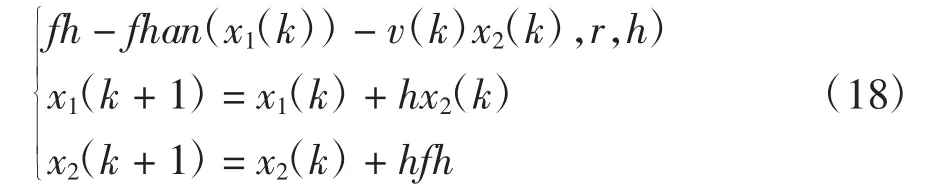
其中，fh-fhan（x1，x2，r，h）是最速控制综合数，其目的是为了快速的获取微分信号，以及避免高频震荡其表示形式如下：

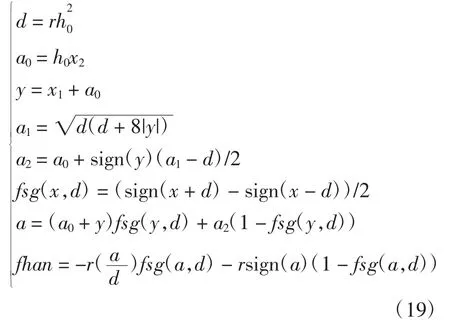
其中，h为积分步长；r为速度因子.

通过构造合适的ESO可以准确地对系统的状态变量以及扩张状态进行实时预估以及扰动补偿，将积分器串联型作为反馈系统的标准型，并且ESO不依赖描述系统传递关系的具体模型[8].ADRC最核心的部分就是ESO.

对于二阶非线性系统：

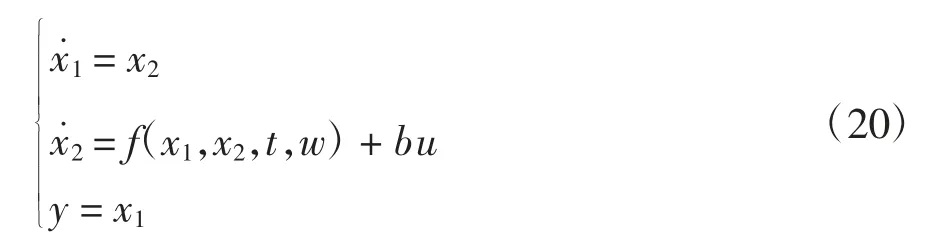
可扩展出额外的状态x3=f（x1，x2，t，w），并设置如下ESO：

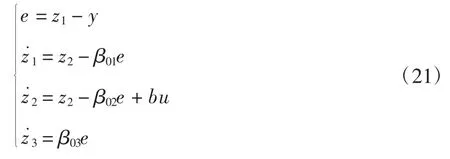
其中，z1、z2和z3分别为x1、x2、x3的观测值；β01、β02和β03为ESO需要设计的参数.

得到上述观测量后可设计如下NLSEF：

其中，

2.2 控制系统设计

机械手控制系统的主要输入量为位置，其最终的目标是准确、快速并且无超调的将给定负载带动到指定位置.位置伺服控制系统控制结构是包含位置环、速度环和电流环的三环控制结构[9].控制原理如图2所示.

电流环为最内环，用来控制电机的转矩，动态响应最快；速度环为次外环，用来控制电机转速，响应速度次之，其输出为电流环的给定；位置为最外环，包含速度环和电流环.位置控制输入依次经过位置控制器、速度控制器和电流控制器的调节，再通过矢量控制，输出电流来控制直流电机的运行.这样由内到外的多环控制结构稳定，可综合利用内外环控制器的作用，保证伺服控制系统良好的动态特性和稳态精度.

在Matlab中进行系统仿真[10]，其中包括了速度、位置控制器，电流控制器以及直流电机的模型，同时进行了变量的监控，用于实现仿真数据的输出，控制算法系统建模用s-function实现.

图2 系统控制原理Fig.2 System control principle

3 仿真研究

为验证控制算法的合理性，特进行仿真实验研究.分别设置如下控制器参数，速度位置控制器中，TD参数为r=5.76E10，h=0.001，h0=0.02；ESO参数为h=0.001，β01=500，β02=5 000；NLSEF参数为k1=102 400，k2=640，b=2 386.6.电枢电流控制器中，ESO参数为h=0.000 1，β01=4 000，β02=40 000；NLSEF参数为k1=2 000，b=1 000.

将正弦信号作为输入信号，并且在t=0.5 s时加入扰动，观测两种控制算法对正弦输入的跟随能力.图3为PID跟随曲线，图4为ADRC跟随曲线.很明显可以看出，两者在有干扰输入的情况下，ADRC的跟随效果远远好于PID的跟随效果.

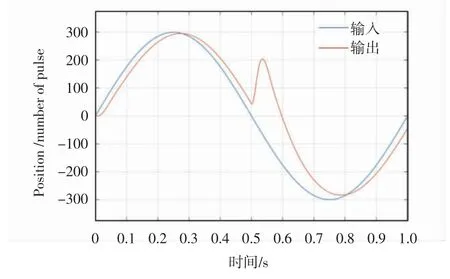
图3 PID跟随曲线Fig.3 PID follow-up curve

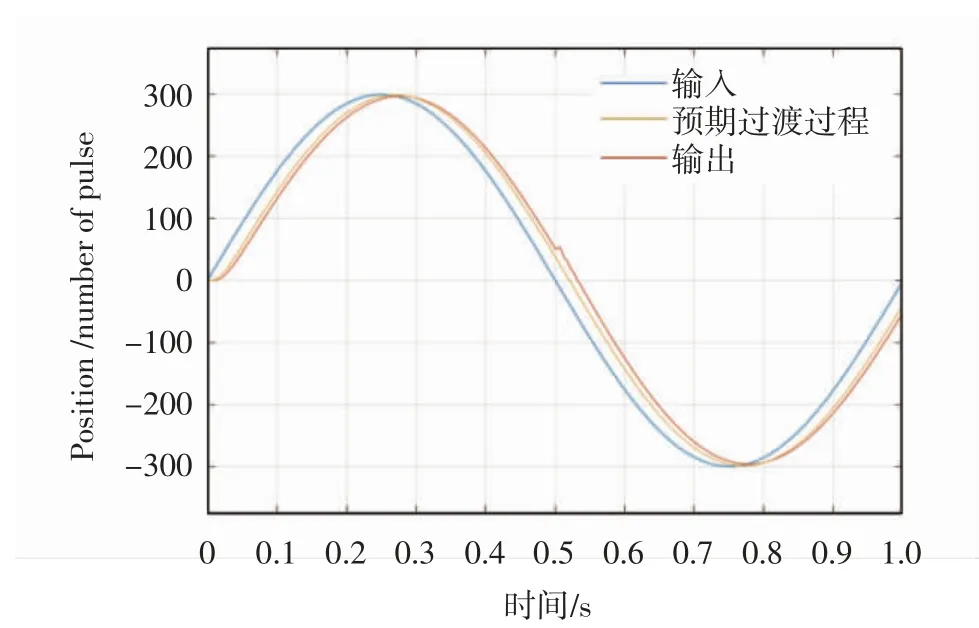
图4 ADRC跟随曲线Fig.4 ADRC following curve

4 柔性控制实验验证

为了进一步验证控制系统设计的合理性，进行硬件实验的研究.

系统的主控芯片为STM32F3系列的ARM微处理器，承担着算法运行、传感器数据采集、通信与命令交互等多种任务[11-12].电机驱动模块的基本原理是H桥.码盘编码器用来测量电机位置和转速.通信协议为基于RS485的Modbus协议.DC-DC稳压芯片用来对电源电压进行管理，以实现较高效率的电压稳压，6 V电压作为电机供电电压.RealViewMDK作为其固件的开发工具.

主程序为一个死循环，死循环中实现对部分程序模块的调用，其他程序模块通过调用时基中断实现，通过全局变量来实现参数的传递.系统中的两个控制器均采用ADRC算法，包括电枢电流ADRC控制器和位置转速ADRC控制器.

对机器人来说柔性控制非常重要，机械手抓取东西时，目标物体的形状和位置往往不是很精确，所以当物体所受力超过一定程度的时候，需要系统将这个力维持在一定限度内，而不是通过位置环来继续增加力，这样可避免对所抓取物体造成损坏.所以在程序运行过程中涉及对电流给定值的判断，实现限制电流，限制力矩的作用.系统程序流程图如图5所示.首先获取位置给定和当前的实际位置，同时读取当前速度值，然后利用位置速度ADRC算法获取电流值的给定.读取实际的电流值，进一步根据ADRC算法实现PWM的调整.为了实现柔性控制，程序中加入了对电流的限幅算法，限制电流幅度的大小可以通过主控芯片来实现.

对系统主要模块进行调试后，进行了柔性控制实验.

用一个物体阻挡住电机，控制系统输入位置，这个时候输出位移由于阻挡作用的存在，所以位置没有发生变化，如图6所示，此时电流会增加.由于设计了柔性控制，电流值如果不在预先限定的电流范围内则不会增加（设置的限流是100 mA）.如图7所示.如果移动阻挡物，则电流保持基本不变，而电机随着阻挡物运动，进而实现了柔性的控制.

图5 柔性伺服电机控制流程图Fig.5 Flow chart of flexible servo motor control

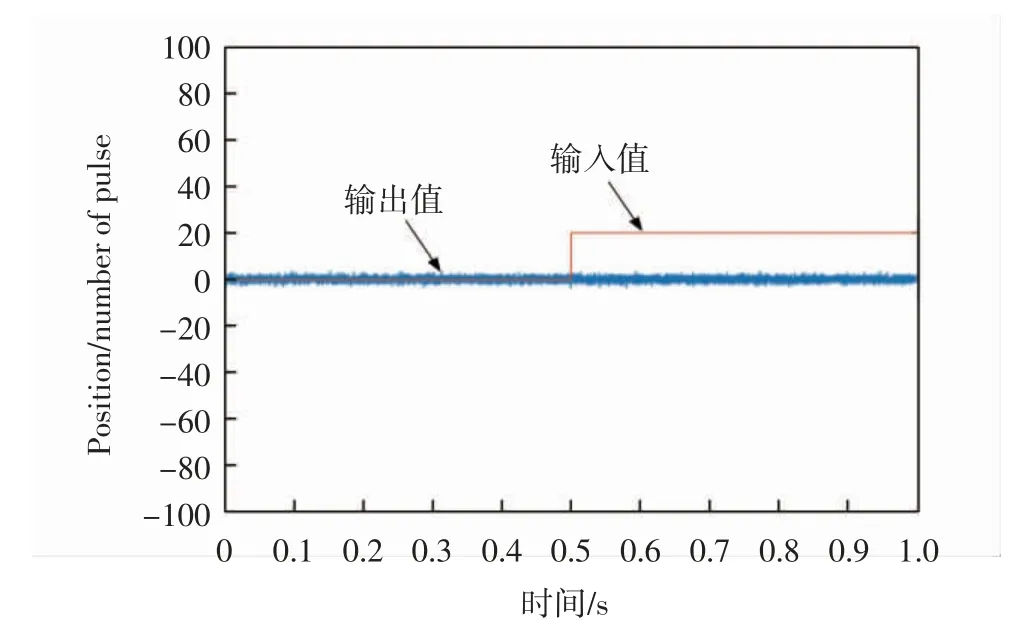
图6 位移变化曲线Fig.6 Displacement change curve

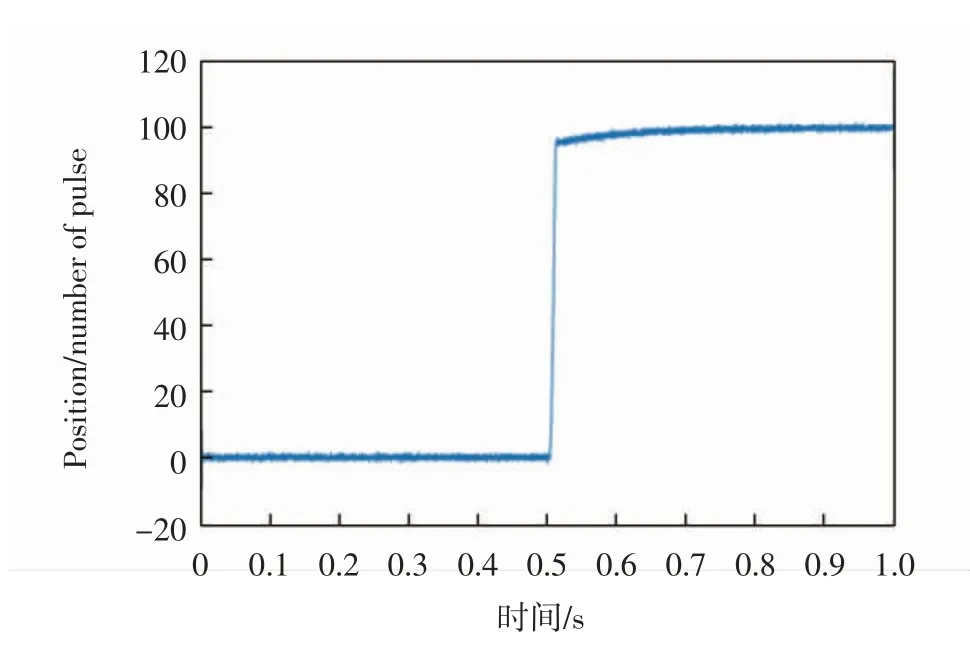
图7 电流变化曲线Fig.7 Current change curve

5 结论

对微型直流电机的柔性伺服控制系统进行了研究，主要包括电机模型的建立、控制算法的仿真以及实验验证.首先介绍了微型电机柔性伺服控制的重要性，并且针对其使用场景提出了高精度、抗干扰以及柔性控制的需求.然后对PID和ADRC算法进行了介绍.并基于建立的电机模型，利用MATLAB仿真软件对PID和ADRC算法进行了仿真.对比了不同场景下两种算法的控制效果.进而设计了控制系统的硬件电路，实现了ADRC算法的嵌入式移植.基于此电路板实现了柔性控制.