基于云重心法修正的供应链联盟收益分配优化研究

董兴林，杨晓丽

（山东科技大学 经济管理学院，山东 青岛266590）

0 引言

随着国民经济水平提升、消费者消费水平提高以及企业间竞争的加剧，市场需求越来越呈现出多样化的特征，产品生命周期与市场周期越来越短，传统的单个企业的生产运作模式越来越不适应市场变化，需要制定一种公平合理的、每个企业都接受的收益分配方案，使每个参与供应链的企业都能获得比自己独立运营更多的收益，这样才能使供应链上的每个企业都能积极参与到供应链中，整条供应链才能持续稳定运行。因此，收益分配问题已成为维持供应链长久稳定发展的关键问题。

目前，在供应链联盟利益分配机制问题上，定量研究方法有Weber集[1]、模糊Owen联盟值[2]、Selectope解[3]、Shapley值[4]等分析方法，各有利弊。被广泛运用于多人合作对策中收益分配计算的Shapley值法，其原理比较公平。Shapley值法主要以供应链成员的边际贡献为依据进行分配，随着联盟合作的深化，成员之间的联盟地位差距逐步缩小，联盟成员为联盟运营所做出的其他努力因素对利益分配的影响日益增大。因此，传统的Shapley值方法已不再适应日益发展的供应链联盟的收益分配问题。李林等[5]将过程阶段思想引入供应链收益分配，基于利益分配的动态均衡构建了三阶段动态利益分配模型。齐源等[6]运用层次分析法和Yaahp软件求出修正因子，对传统的供应链知识共享收益分配机制做出修正。李英海等[7]将变异系数法与Shapley值法相结合，提出多业主梯级水电站补偿效益分摊的变异系数—Shapley值法，实现了各水电站间补偿效益分摊的公平性与合理性，有利于提高各级水电站参与梯级联合调度的积极性，确保流域梯级联合调度效益的最大化。张亚文等[8]发现供应链联盟中的某些企业存在着联结依赖关系，并能为供应链创造额外收益，因而提出一种新的基于这些联结依赖关系的Shapley值修正算法。

然而，上述方法仍存在着一定的缺陷，传统的Shapley值法在经过修正后，虽然在公平性方面已经得到提高，但这些方法仍然忽略了供应链上不同企业的创新能力、风险承担能力、资产状况、资源投入等因素的差异，而这些因素都是为供应链带来额外收益的关键因素，这就使得创新能力强、承担更多风险的企业感到不公平，认为自己付出更多的努力而只得到了无差异的回报，参与积极性因而降低，长此以往，供应链联盟必将走向瓦解。

为促进供应链联盟长久稳定的发展，许多学者基于不同要素考量给出了基于Shapley值法的修正算法。马士华等[9]针对企业技术创新对提高供应链整体竞争力的作用提出基于Shapley值法的修正算法，对收益分配方案进行更为公平合理的调整。王岳峰[10]基于贡献率、风险以及投资等因素对供应链收益的影响提出相应的修正模型。林翊等[11]以物流企业的边际贡献度、风险、投资额、任务、服务能力为权重因子，采用TOPSIS法和Shapley值法相结合为物流联盟构建优化的利益分配模型，克服了利益平均分配的不合理问题。上述方法考虑了供应链联盟成员企业之间的个体特征和偏好，对比以往的分配方式更显公平合理。但这些研究又存在一个共性问题，即这些修正算法对指标权重的赋值表现出比较强烈的主观性，对模糊性问题的解决不够客观。因此，如何克服赋值的主观性已成为亟待解决的问题。

基于云理论的云重心法，将模糊性和随机性特征集成在一起，可以有效解决系统定性概念与定量数值之间的不确定性转换，以及评价过程中的主观性、模糊性和随机性强等一系列问题，具有评价过程简单方便的特点。基于此，本文采用Shapley值法对供应链联盟收益进行初分配，然后增加投入成本、风险水平和创新能力3个指标，采用云重心法对收益初分配方案进行修正，从而得到相对客观、公平合理的分配方案。

1 影响供应链联盟收益分配的要素分析

供应链联盟往往涉及一些中小企业、金融机构、物流企业和核心企业，不同角色的企业发挥着不同作用，它们通过联盟形式将优势资源整合在一起，创造出1+1＞2的整体效益。供应链联盟企业拥有不同水平的投入成本、风险水平与创新能力，这些因素成为直接影响联盟企业收入分配的重要因素。

（1）投入成本。一条完整的供应链有赖于各成员的资本、人力、物力等投入，而投入成本则是成员企业参与供应链收益分配的基本要素，投入成本与收益分配呈正比关系。

（2）风险水平。供应链联盟在带来更多效益的同时，也可能带来更大的风险。处于同一供应链上的企业既要“收益共享”，同时也要“风险共担”。但不同成员在供应链中担任的角色不同，发挥的作用各异，它们面临的风险水平也会依据不同的角色而发生变化。一般来说，承担高风险的供应链成员应该得到更高的收益，面临低风险的成员收益分配就要减少。这样一来，面临高风险的成员就会更加积极主动地投入到供应链运营，面临低风险的企业也会为了分得更多利益而努力。

（3）创新能力。创新可以为企业带来规模效益，但供应链企业的创新意识不同，创新能力也会参差不齐。在供应链进行收益分配时，必须考虑创新能力强弱这一因素，才能更好地鼓励创新能力强的企业，同时激励创新能力相对弱的企业，从而在整条供应链内形成良性竞争。

2 供应链联盟收益分配方案描述

2.1 Shapley值法模型

Shapley值法是美国Shapley L.S教授1953年提出的用于解决n人合作对策的一种算法[13]。当有n人从事某项活动时，他们中的任意组合形式都能获得效益；当合作中的人数增加时，并不会引起效益的减少。因此，当全体n人合作时能够获得最大效益，而Shapley值法正是用于解决最大效益分配的数学方法。设集合I=｛1,2,3,…,n｝，若对于I的任一子集S，都有唯一的实值函数V（S）与其对应，并满足：

其中：

那么称［I,V］为n人合作对策，V即对策的特征函数，表示n人合作产生的效益。用φi（v）表示合作I中成员i从合作的最大效益中应得的收益。在合作I情形下，合作对策的分配用表示。那么，若要合作成功，必须满足如下条件：

其中：v （i）为企业不参与供应链而独立经营获得的收益。

用φi（v）表示在合作I的情形下，成员i所分得的实际收益，则在合作I中各成员收益的Shapley值为：

其中：si表示集合I中包含i的全部子集，是子集s中的元素个数，w）是加权因子，v（s）表示子集s取得的效益，v（ si）表示除去子集成员i的子集s所取得的效益。

这种单纯用Shapley值法进行收益分配的方法在实际中往往不会被采纳，因为它是建立在供应链各成员都投入相同的成本、面临同等的风险和实力相当的创新能力等基础之上的，是一种完全理想化的情形。事实上，供应链上的各成员企业财务实力参差不齐，面临的风险也不能简单的平均化，不同企业对待创新的态度不同，其能力也会高低不等。因此，需要对上述方法进行修正。考虑到投入成本（包括资本投入、人力与物力投入）、风险水平和创新能力这些指标不易量化的特点，采用云重心法进行修正。

2.2 云重心法修正模型

云重心法是建立在正态云理论上的一种评判方法，可很好地完成定性指标和定量指标之间的模糊性转换。目前在风险控制和军事领域评估中运用较多，在供应链收益分配方面的运用并不多见。正态云有3个数字特征，分别是表示重心位置的期望值Ex，表示期望宽度的熵En，表示期望厚度的超熵He。用T=a×b表示云重心，其中，a为云重心的位置，即Ex；b为云重心的高度，当出现位置相同的云重心时，可以通过比较云重心的高度来确定隶属云的重要性。a、b发生变化，云重心也会随之变化。

（1）各指标的云模型。在修正模型中需要考虑3个指标，分别为投入成本、风险水平和创新能力，用3个云模型来表示。邀请n位专家赋值，共得到n个数值分别为Ex1,…,Exn。那么，对于各指标云模型的数字特征值Ex、En就可表示为：

Ex1…Exn为n个专家的赋值。

（2）构建三维综合云。3个云模型指标表示之后，可构建一个反映系统状态变化的三维综合云。当系统发生变化时，综合云的位置和形状也会发生变化，用一个三维T向量来表示综合云，即T=（T1,T2,T3），其中，Ti=ai×bi,i=1～3，ai表示第i个指标的期望值Exi，bi表示第i个指标归一化后的权重。当系统发生变化，云重心变为

（3）确定指标权重。为减少人为因素的影响，采用排队论方法确定权重，首先邀请专家对各指标的重要程度i进行排序，排队等级i越小，表示指标越重要[14]；i相等，则重要程度相同。

（4）计算加权偏离度。综合云的理想状态是指供应链联盟系统中投入成本最多、风险水平最高、创新能力最强的一种状态，此时的云重心表示为：

其中：a'表示理想状态下各指标的期望值Ex。

对三维综合云向量T进行归一化处理，计算如下：

加权偏离度计算如下：

其中：θ越大，表示偏离程度越大。

（5）确定收益修正系数。由于原Shapley值法假定供应链各参与方的各个指标值都是均等的，这显然不合理，因此需要在原Shapley值的基础上进行修正。首先对θ进行归一化处理，得到θ*：

其中：ΔRi表示各参与企业修正后的指标权重。

（6）确定收益修正值。

其中：v （I）表示供应链成员都合作下的收益值。

3 算例分析

假设现有的供应链联盟中有3个成员，分别包括企业1、企业2、企业3。当3个企业都不进行任何合作，只通过自己的努力生产时，3个企业均只获得10万收益。当企业1与企业2合作时，可获得收益30万；当企业2与企业3合作时，可获得收益25万；当企业1与企业3合作时，可获得收益40万。当3个企业同时合作时，可获得收益65万。

3.1 Shapley值法收益计算

已知v（1）=v（2）=v（3）=10，v（ 1,2）=30，v（ 2,3）=25,v（ 1,3）=40,v（ 1,2 ,3）=65。以企业1为例，由以上信息及式（6）可列表计算得到相关结果，如表1所示：

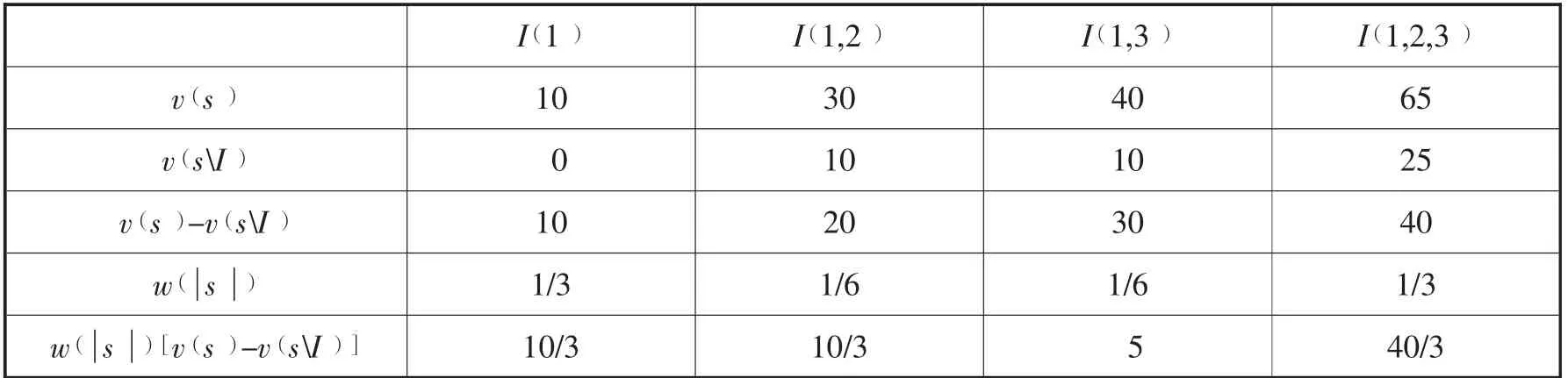
表1 企业1的Shapley值法收益分配

根据式（5）将列表的最后一行相加可以求得φ1（v）=25，即当供应链上的3个企业在通力合作的情况下，若用Shapley值法分配收益，企业1可以分得25万元，用同样的方法求得企业2可以分得17.5万元，企业3可以分得22.5万元。

经验证，以上结果均满足条件（1）、（2）、（3）、（4）。显然，在成立供应链联盟的情形下，企业之间实现了优势互补，创造了规模效益，每个企业获得的收益都得到了显著增长，这是供应链联盟向好发展的一个重要因素。

3.2 云重心的Shapley值法供应链联盟收益分配

云重心法的关键一环是需要专家对企业的各项指标进行评价。因此首先需要邀请4位专家对3个企业的各项指标进行评价。以企业1为例，结果如表2所示：

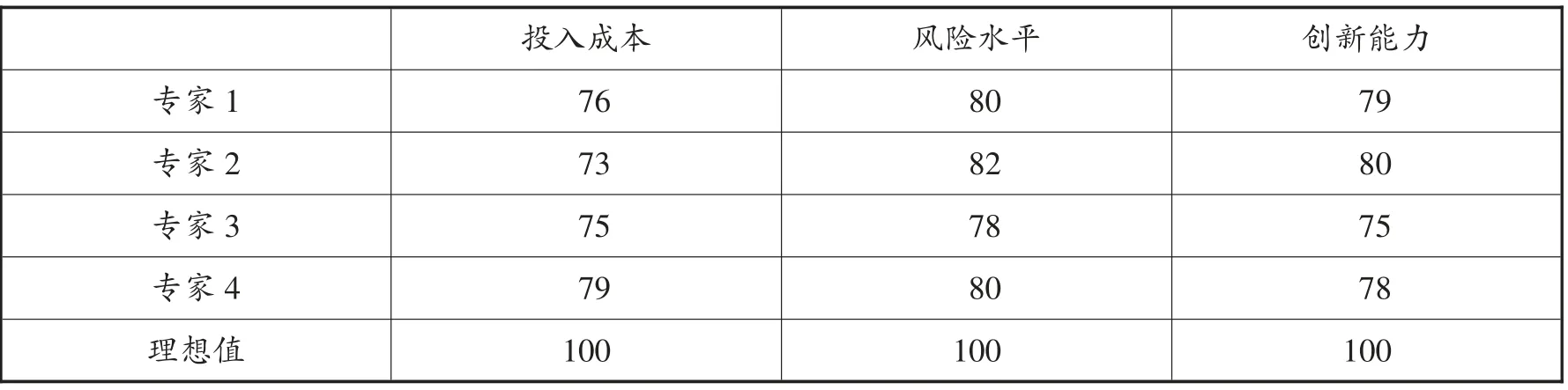
表2 企业1的各项指标评价

根据式（7）、式（8）计算各指标的期望值和熵，结果如表3所示：

表3 企业1各指标的期望值与熵

由式（9）计算企业1的各指标权重并对其归一化，结果如表4所示：

表4 企业1各指标权重

根据式（10）计算得出，当处于理想状态下，综合云的云重心表示为：

根据式（11）对云重心T=（34.32,25.76,17.6）进行归一化处理，得到云重心向量：

根据式（12）计算加权偏离度，得到：

重复以上步骤，可以计算得到企业2与企业3的加权偏离度分别为：-0.30和-0.38。对供应链联盟中的3个成员企业的加权偏离度进行归一化处理，得到企业1、企业2、企业3的加权偏离度分别为：

根据式（13）对各企业的指标权重作出修正：

根据式（14）确定各企业的收益修正值，得到：

根据式（15）确定各企业修正后的最终收益值：

下面，对不同的收益分配方法进行对比，结果如表5：

表5 各分配方案对比

首先，通过供应链联盟这一形式，将各企业的优势资源进行整合后，各企业的收益得到明显增加。不难看出，联盟要比不联盟获得更多的收益。其次，利用云重心法对Shapley值法的分配方法进行修正后，得到各企业的收益分配额分别为31、11.5、22.5。其中，企业1收益得到明显增加，这主要是由于企业1的创新能力、投入成本和风险水平都比较高，对供应链各方面的贡献都比较大；企业2的收益明显下降，主要是由于其创新能力落后，而创新能力又是3个修正指标中最重要的要素；企业3收益保持不变，这是由于其各项指标都比较平均。不难理解，这样修正过后的分配方法不仅在收益分配方面表现地更加公平合理，更有利于为供应链联盟创造良好的发展环境，保障了供应链的长远发展。

4 结论

传统的联盟收益分配方式已经与快速发展的供应链联盟日渐脱节，迫切需要一种更加公平合理、能激发联盟成员企业的收益分配方案。考虑到联盟内成员企业的各项能力参差不齐，本文引入创新能力、成本投入和风险水平3个修正因子，采用云重心法对Shapley值法的初分配结果进行修正。

研究结果显示，传统Shapley值法的分配结果经过云重心法修正后，各成员企业的收益发生了明显变化，收益差距拉大，直观上更能分辨出各企业的能力差异。该方法意味着从“能者多劳”到“能者多得”的转变，一方面更有利于激发供应链联盟成员企业的积极性；另一方面，对于各项能力稍弱的、收益分配较少的企业，也能鼓励它们积极发展自身各项能力，加大各项投入，减少“浑水摸鱼”的可能性，这更有利于供应链联盟的长远稳定发展。