考虑顾客放弃的多渠道联络中心排队模型

马 标，李军祥，张智铀

（上海理工大学 管理学院，上海200093）

0 引言

近年来，随着社会通讯网络的发展，联络中心在电信、金融、酒店以及银行等服务行业发挥着越来越重要的作用，联络中心中一个重难点是在保持服务质量的同时提高经济效益，因此对联络中心考虑等待、放弃和成本的研究尤为重要。

联络中心运行过程中会发生顾客的等待时间过长而导致顾客放弃排队，对联络中心的运营效益产生一定的影响。戴滔、霍佳震[1]采用仿真方法对呼叫中心的单技能和多技能座席人员进行了运营效率评估；Mandel等人[2]研究和分析了一些考虑顾客直接放弃和中途放弃的多服务台排队模型，在此基础上进一步分析了顾客的等待和放弃对联络中心的效用的影响；Yu等人[3]给出了带有延迟通告和重试的联络中心流体模型；秦海林等人[4]给出了带优先权与不耐烦顾客的联络中心排队模型；臧万斌等人[5]通过设置顾客的耐心阈值并考虑为会员顾客增加特定的座席渠道，或在原有的人力下调整座席渠道数量，在传统呼叫中心模型的基础上建立新型的云联络中心服务排队设计[6]。

本文在前人的研究基础上，通过对多渠道联络中心排队流程的分析，利用Matlab进行仿真计算在同等座席下的传统单渠道呼叫中心和多渠道联络中心的性能指标。

1 多渠道联络中心

假设联络中心存在两类顾客，第一类是即时信息顾客，包含使用电话等呼叫的顾客；第二类是可延迟信息顾客，包含微信、E-mail等信息的顾客。多渠道联络中心的排队流程如图1所示，其中放弃服务的顾客包含因系统容量限制，直接退出的顾客和因考虑顾客耐心值中途退出的顾客，同一渠道的顾客满足先到先服务的原则（FIFO）。重排过程是可延迟信息渠道的顾客因即时信息渠道顾客具有强制优先级而重回系统排队的过程。

2 模型假设

为保证联络中心系统的稳定性，做如下假设：

假设1：t时段各渠道顾客的到达过程均服从相互独立的泊松分布，第i渠道的顾客到达率λi（）t，各渠道的服务均服从相互独立的指数分布，参数为μi（t），ni（t）表示i渠道服务的座席数量，ρi（t）表示i渠道的服务强度，则t时段i渠道的等待概率pi（t）为：

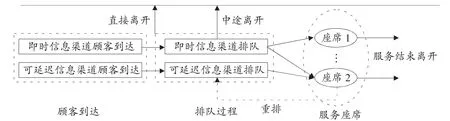
图1 多渠道联络中心到达过程

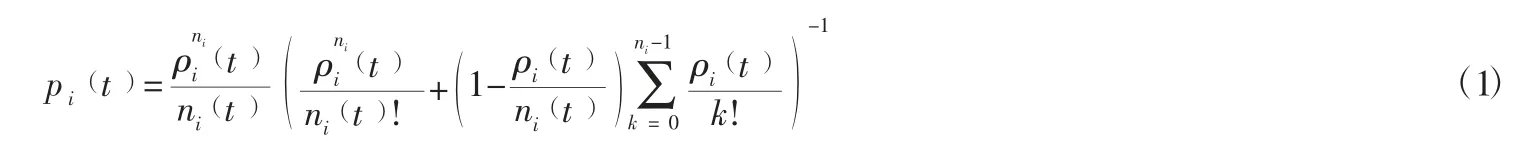
假设2：多渠道联络中心第i渠道t时段的排队队长li（t）是由该时刻到达的顾客队长λ'

i（t）加上一时段的队长（t-1）再减去队列中进入座席服务的队长gi（t）后加即时信息渠道的顾客，具有强占优先级。而可延迟信息渠道的顾客返回队列重新排队等待的队长wi（t），即：

假设3：顾客i渠道单位时间的放弃率θi（t）与联络中心的等待概率pi（t）有一定关系。为保证服务的稳定性，假设Ni为i渠道的顾客总数，Si（t）为t时段i渠道到达系统的顾客数，服务全部顾客所用的时间为T。联络中心中放弃的顾客数包括直接和中途放弃的顾客数之和，即多渠道联络中心放弃总人数A （t）为：

3 模型构建

本文研究的模型为考虑顾客放弃的多渠道联络中心，从座席成本、等待成本和放弃成本三个方面分析联络中心的运营成本。令联络中心的i渠道的单位座席成本为ci，单位等待成本为ciw，单位时间的放弃成本为cia，则座席成本、等待成本和放弃成本分别为：。这样，考虑顾客放弃的联络中心的总成本最小化模型为：

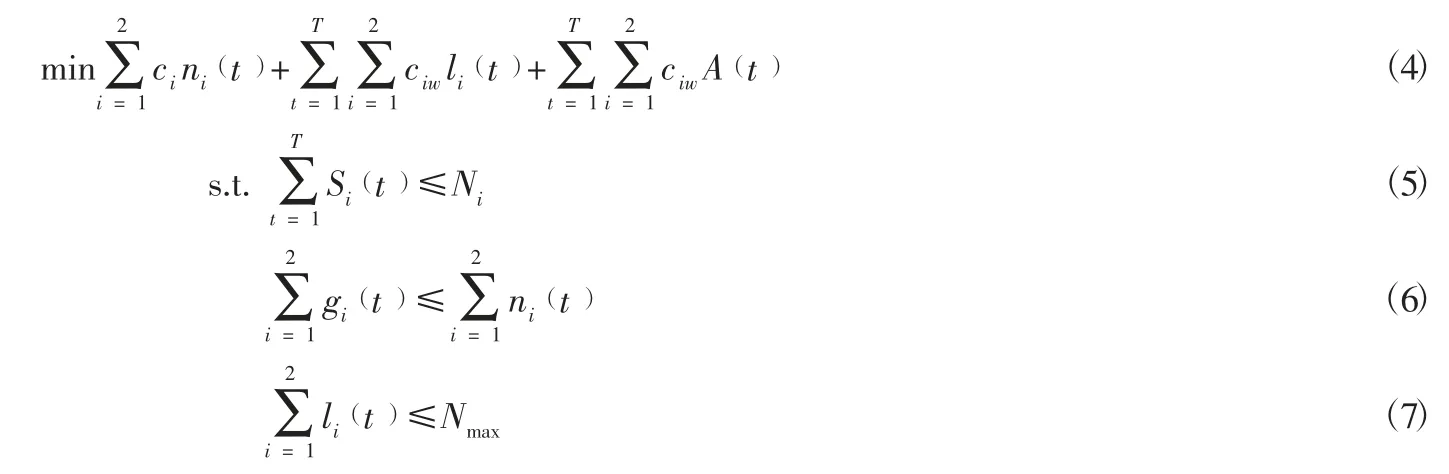
其中：式（5）表示到达系统服务的顾客总数量不能超过顾客总数，式（6）表示t时刻进入到座席服务的顾客数量小于等于总座席数量，式（7）表示t时刻排队队长要小于系统排队等待队列的系统可承载的最大队列长度Nmax。

4 仿真实验

本文讨论考虑成本问题的传统单渠道呼叫中心与多渠道联络中心。设定单渠道呼叫中心参数：仿真顾客总人数为3 000人，到达率为20人/分钟，服务率为2人/分钟。设定多渠道联络中心参数，两个渠道的仿真总人数分别为N1=2 000人和N2=1 000人，到达率分别为λ1（t）=15人/分钟和λ2（t）=5人/分钟，服务率分别为μ1（t）=2人/分钟和μ2（t） 1人/分钟。对传统单渠道呼叫中心和多渠道联络中心进行Matlab系统仿真，其仿真计算结果如表1所示。

由表1可知在即时信息渠道的平均等待时间和放弃率小于传统单渠道呼叫中心。随着座席配置的不断增加，顾客放弃率变化降低，趋于稳定。根据座席配置变动下策划成本的边际效应，当座席人数为23人时，多渠道联络中心的总成本最低为5 645.33元。

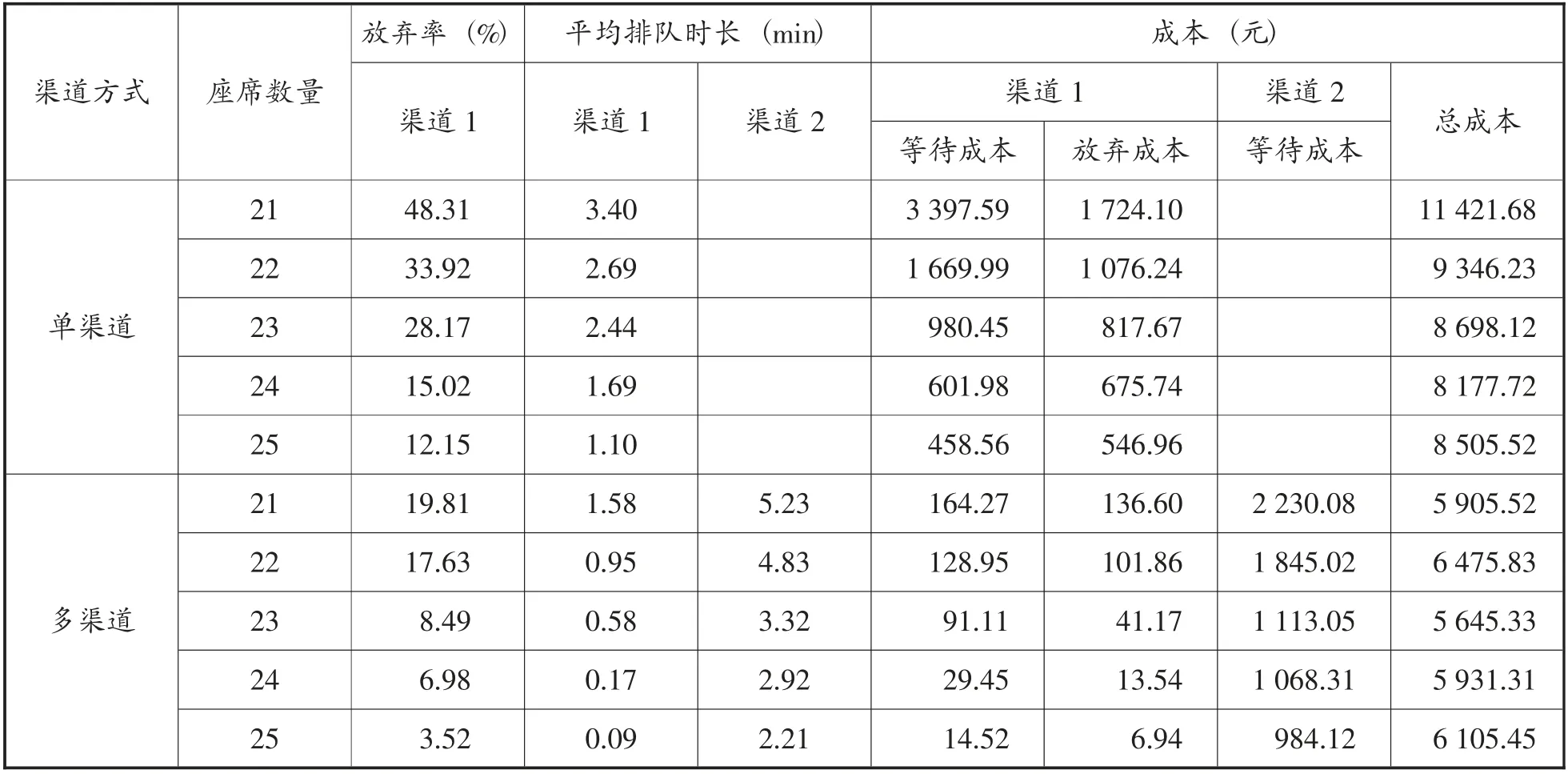
表1 传统单渠道与两渠道联络中心性能指标对比

5 结束语

本文考虑顾客放弃的多渠道联络中心，从座席成本、等待成本和放弃成本三个方面，对传统单渠道呼叫中心模型和具有优先权的多渠道联络中心模型人力效能进行对比研究。通过分析可知，在同等座席数量配置下，相比传统呼叫中心，有优先权的多渠道联络中心等待成本和放弃成本所占总成本中比例较少，故多渠道联络中心更符合时代的需求。