浅析Little's Law及其在准时化生产中的应用

林 兵，林宇辰，孙 影

（1.江苏师范大学 商学院，江苏 徐州221116；2.苏州大学 文正学院，江苏 苏州215104；3.徐州工程机械集团，江苏 徐州221000）

0 引言

通过参观徐州工程机械集团（简称徐工）下属某制造厂，并与生产车间管理人员交谈中得知徐工生产的起重机是由成千上万的零部件组成，管理起来相当困难，他们希望通过加强物流管理来进一步提升车间物流效率。在与企业相关人员座谈时，认识到了库存管理对制造企业的重要性，徐工也在使用存货周转率（Inventory Turnover）这个指标对工厂里的库存进行管理。存货周转率作为衡量资产管理能力的重要财务指标早已被众人所熟知，但不被大家熟悉的一面是，它实质就是Little's Law（LL）在财务中的体现。

LL中的第一个L取自麻省理工学院教授John D.C.Little，第二个L是因为他于1961年在Operations Research上发表了关于排队公式L=λW的严格数学证明，使之成为排队论的一条基本数学定理。在过去的30年里，LL在运作管理领域得到了广泛的应用。更进一步，Hopp and Spearman（2000）把LL作为运作管理的一条基本原理。LL之所以受到学者和业界广泛重视与应用，首先是因为它作为分析工具即简单又十分强大，其次在理论上，它联结了库存理论和排队论，而库存理论与排队论可以说是运作管理这门学科的基础。

1913年，Harris将经济订货批量模型（EOQ）应用于物料库存管理，可看作是库存管理这门学科的起源。到了20世纪50年代，Arrow et al（1951）将动态规划应用于军事后勤中的库存管理，极大地推动了库存理论研究。与此同时，以“零库存”为极限目标的准时化（Just-In-Time，JIT）生产模式在日本丰田汽车公司诞生。20世纪80年代末，全球经济处于低迷期，一些跨国公司开始专注于核心业务的投资以提高投资回报率，而把非核心业务外包出去，从而大幅度提升了业绩，其他企业则纷纷效仿，逐渐形成了供应链思想，而供应链管理则把库存管理从以往的单点库存管理拓展为网络化库存管理。而且在运作管理的数学模型中，库存控制可谓是最典型的美式运作管理方法（Hopp and Spearman，2000），另外，实践中也有类似的观点，即“生产管理就是库存管理”（小林俊一，2012）。可见，无论美式运作管理，还是日式JIT思想，库存都是核心。

生产运作就是流程，是从原材料变成产品和服务的流程（陈荣秋和马士华，2017）。从运作管理来看，任何组织都是由业务流程组成，而流程的运营绩效可通过流程时间（Cycle Time/Flow Time，CT）、通过/产出率（Throughput,TH）和在制品库存（Work-In-Process,WIP）来度量（Anupindi et al，2011）。任何运营系统的基本活动就是流程中某种实体在流动，这些实体可以是制造系统中的零部件，物流系统中的货物，学校的学生，医院的病人，财务系统中的货币，计算机与通信系统中的访问要求，等等。所以，对制造系统、服务系统、财务系统、物流与供应链系统的流程可用排队模型来描述，并用排队优化理论对流程管理进行优化。而制造系统运作管理则更多地结合了库存与排队理论。

具体到LL，它是如何联结流程/生产运作的三个绩效度量指标？如何使用LL分析实际问题和提升运营绩效？以下将紧紧围绕这两个问题展开讨论。本文将依次介绍LL在排队论和运作管理领域的不同表达形式，并以LL在运作管理中的应用为主要研究内容，利用LL分析出提高运营绩效的路径，并以准时化生产为例来阐明该路径的有效性和可操作性。

1 Little's Law和Variability

排队论中LL表述为：在稳定状态条件下，排队系统中某种物品平均数量等于该物品平均到达速率乘以该物品在系统中的平均逗留时间。记为：

L：排队系统中物品的平均数量；

λ：物品到达排队系统的平均速率；

W：物品在系统内的平均逗留时间。

则LL的数学表达形式为：

如果用排队模型M/M/1来说明，有：

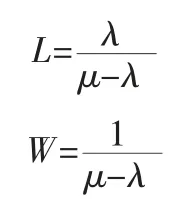
很明显，式（1）成立。对式（1）还可如此理解：一个参照物品到达排队系统，经过W时间后离开系统，在此期间，它将看到λW个物品出现在系统内，且无论任何时点到达该系统，该参照物品都将看到λW个物品，所以，排队系统中物品的平均数量是λW，式（1）成立。式（1）式最早出现在Morse（1958）中，随后，Little（1961）对该公式进行了严格的数学证明。以后，又有很多学者对LL做了各种证明与拓展。目前，LL在运作管理与计算机系统结构领域得到了最为广泛的应用（Little，2011）。

LL在运作管理中的表现形式是将流程的运营绩效度量流程时间、通过/产出率和在制品库存联系在一起的关系式，即：

或简写为：

比较式（1）和式（2），式（2）中WIP、TH和CT相当于式（1）中的L、λ和W。在LL两种表述中，式（2）使用产出率TH而不是式（1）中的到达率λ，更是体现了运作系统，特别是制造系统的特点。所以，也可将式（2）写作：

首先，分析LL在财务中的表现形式。前面提到存货周转率是财务常用的衡量资产利用效率的财务指标，具体公式是：

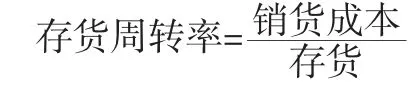
变换上式，得：

在式（4）中，存货对应着以货币计价的在制品库存，可用年初库存和年末库存的平均数来估算；销货成本是已售出产品的成本，包括原材料、劳动力及制造费用，代表以货币为单位的产品年产出率；存货周转时间则是以年为单位的流程时间，是存货售出前被搁置的平均时间。所以，式（4）就是LL。其他一些财务指标，如，应收账款周转率=赊销额/平均应收账款，应付账款周转率=销货成本/平均应付账款等也都是LL在财务管理中的体现。

LL在服务运作系统，如银行、医院、机场、餐馆、超市、学校等也有着广泛的应用。陈荣秋和马士华（2017）以学校为例很好地说明了服务系统的LL，即：

大学在校本科生数量相当于在制品库存，每年入学或毕业本科生数相当于产出/通过率，而4年是流程时间，即本科生从入学到毕业需在大学系统逗留4年时间。

LL也有助于分析物流系统，如物流配送中心。著名时尚品牌Zara的全球物流配送中心是其供应链的核心枢纽，正常情况下，物流中心每周运营4天，成衣在物流中心逗留8小时后就被配送出去（Ferdows et al.2003），而每周成衣通过量是2.5百万件（Simchi-Levi et al.2007）。基于以上信息可知：

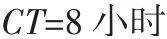
假设每天10小时工作制，则：

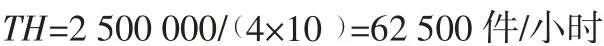
由LL可知：

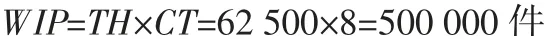
可以看到此时LL的作用是，当已知两个参数，很容易得到第三个参数，而这个未知参数可能在实际问题中不易被测量。

对于制造系统，可把工厂、生产车间、一条生产线、一个工作站、一台机器分别看作流程，使用LL进行分析。生产运作系统特别关注运营效率问题，以下用LL来说明系统效率。根据式（3），实现同样的产出率10，第一个生产运作系统需要：

而第二个系统可用更少的在制品库存和更短的流程时间来实现，如下：

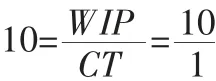
很明显，第二个系统比第一个运营效率更高。对于相同产出率，第二个系统能做到使用更短的CT和更少的WIP，原因在于：第二个系统的不确定与可变因素（Variability）比第一个系统的要小。

运作系统往往存在大量Variability。Variability包涵两层意思，一是指存在的不确定性，二是考察对象在量上有变化。例如，时尚服装需求存在很大的不确定性，也可以说，时尚服装需求的Variability很大；而每天的用电量即使很确定，但早、中、晚三个时段的用电量有起伏，这就是可变性。运作系统的Variability主要来自需求过程与生产/供给过程，而运作管理的重要任务就是应对运作系统的Variability。应对方法分为两类，一类是主动降低法，如日本丰田汽车的准时化（Just-in-Time,JIT）生产，就采用各种方法积极主动地降低Variability；另一类是缓冲法，即采用库存、产能和时间来缓冲Variability。

由以上分析知，在产能固定的情况下，实现JIT生产提高运作系统运营效率的关键在于降低该系统的Variability。下面，基于LL，以某工厂的生产车间为例来讨论如何实现JIT生产。

2 准时化制实践

JIT生产是实现库存高效管理、提高产品质量的有效途径，有大量的成功案例，例如丰田汽车、戴尔电脑、Zara等，他们的生产模式特别值得我国企业借鉴。下面具体到车间生产与物流来讨论如何实现JIT。将某作业车间整体看作一个流程，把车间场地看作服务站，需加工或装配的零部件看作需求流，零部件的加工就是被车间服务，加工完毕的零部件流出车间，流程如图1所示。

实现JIT要采用拉式系统。众所周知，物料需求计划系统（Material Requirements Planning,MRP）是典型的推式系统，而丰田汽车的JIT生产采用了拉式系统。MRP出现在20世纪60年代，是IBM将计算机应用于生产与库存管理的产物，而丰田的JIT代表了消除浪费、精益求精的生产思想，拉式与推式运作管理方法有显著差别。但市面上对拉式系统仍有很多的误解，例如，一个常见的错误看法就是，拉式生产就是客户订单需求拉动了生产，把拉式生产等同于按需求生产（Make-to-Order,MTO），这显然不对，因为，MRP做生产计划既基于预测的需求，还有客户订单；极端情况下，MRP可以完全按订单组织生产。

那么，拉式系统与推式系统的主要差异在哪里？Hopp and Spearman（2004）特别指出这两种系统的本质区别是：拉式系统对在制品库存做了明显的限制，而推式系统没有。在生产控制方面，拉式优于推式的原因在于拉式有意图地限制了系统内的WIP数量，如丰田生产系统是通过有限的看板实现对WIP的限制。了解了拉式系统优越性的本质原因后，可用更简单的CONWIP拉式系统（如图2所示）来替代较复杂的看板系统。

图1 生产车间运作流程示意图

图2 CONWIP拉式系统

当WIP（比如车间里的零部件）离开车间而减少了x单位，相关控制信息由输出端传到输入端，提示应释放x个单位物件进入车间，这样车间中的WIP总量始终保持为一个固定量，这就是CONWIP控制。CONWIP系统只在输入、输出点进行控制，这比看板系统通过设置看板对系统内各储货点WIP实施限制要简单。

拉式系统还有一个优点，那就是它的强壮性，这意味着它对WIP限制量（WIP limit）的大小不很敏感，这使得建立拉式系统和实施拉式生产更具实践操作性。在确定WIP的限制量后，回看式（3），增加产出率TH=WIP/CT，要么增加WIP，要么需减少CT，由于WIP受到限制，对于拉式系统或JIT生产就只能通过降低CT来增加产出率。另外，产出率在很多情况下是外生变量，也就是说，产出率对运作系统来说是事先给定的，此时要提高运营效率，只有降低CT，降低CT就要降低系统流程的Variability，而CT缩短后，WIP会减少，库存的减少将会暴露系统更多的问题，找到这些问题有利于对症下药，并采取相应措施继续降低Variability，这样就形成持续改进的循环，这一逻辑关系如图3所示。

实施拉式生产要估计WIP限制量（WIP limit）。下面，通过追踪车间零部件物流对WIP限制量进行估算。可使用射频识别技术（Radio Frequency Identification,RFID）对零部件尤其是重要零部件进行实时追踪。可把RFID标签附着于盛放一般零部件的容器，或直接附着于重要的零部件上。这样可以很容易测量每天有多少数量零部件（记为N）通过了该生产车间，如果每天工作小时数为t，每小时通过率可以很容易估计出来，记为：

图3 准时化生产的逻辑

则该批零部件的平均流程时间CT是：

最后，每天平均在制品库存可由LL估计：

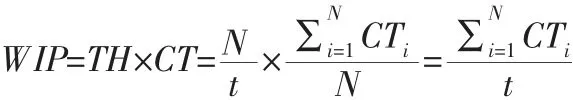
由上可知，WIP是该批零部件流程时间总和与每天工作小时之比。此后，还可再根据实际情况对以上估算的WIP做相应调整。

3 结论

本文通过分析运作管理的基本原理Little's Law及其在运作管理中的应用，为我国企业提升运作系统绩效提供了理论依据。本文的主要结论是系统运营绩效取决于系统的不确定与可变因素（Variability），只有降低系统的Variability才能提高绩效，而准时化生产是降低Variability提高运营绩效的有效途径。最后，以生产车间为例，讨论了实现准时化生产的拉式系统。