核工程钢板混凝土墙防撞击贯穿实用计算方法*
2020-10-23刘晶波韩鹏飞王晓峰李述涛
王 菲,刘晶波,韩鹏飞,3,宝 鑫,王晓峰,李述涛
(1. 清华大学土木工程系,北京 100084;2. 陆军工程大学国防工程学院,江苏 南京 210007;3. 国质(北京)建设工程检测鉴定中心,北京 100081))
安全壳作为核电站的安全屏障,可有效抵御飞机撞击、剧烈气流(龙卷风或者飓风)带来的飞射物撞击、恐怖爆炸袭击等危险事件并为内部设备提供保护。钢板混凝土结构具有良好的受力性能和抗冲击性能,此外在建造、安装等施工方面效率较高,能很好地满足核电工程快速发展的需要。目前,钢板混凝土结构作为安全壳的重要组成部分被有效用于第三代核电站中。
自2001 年“9.11”恐怖袭击事件后,美国核能管理委员会、核能研究院和能源部以及我国核安全局相继出台相关规范,明确规定核电站设计必须考虑大型商用飞机的事故型和恐怖性撞击作用[1-4]。目前学者们对大飞机撞击核电站结构问题已开展了一系列研究工作[5-9],获得了大飞机撞击下核电结构动力反应的一些规律和特点。在撞击速度一定时,如果安全壳结构设计不够合理,就有可能发生贯穿事故。对于核电站安全壳这种带对拉钢筋的双钢板混凝土结构形式,目前对相关的贯穿公式研究较少,可直接用于工程中的防贯穿实用计算公式更为缺乏,从而给核电站安全壳防贯穿设计带来了较大困难。现有相关文献和研究报告中,比较有代表性的是Bruhl 等[10]的研究工作。Bruhl 等针对钢板混凝土墙的防贯穿问题,提出了“三步”法,该方法可用于计算钢板混凝土墙在抵抗弹体贯穿破坏时所需的最小钢板厚度。Bruhl 等利用该方法对130 个弹体撞击钢板混凝土墙的实验数据进行了验证。结果表明,在98%以上的实验中,该方法的计算结果与预期结果一致或保守,但“三步”法未考虑双钢板混凝土中对拉钢筋或者栓钉的作用,计算结果偏保守。此外,由于已有的实验数据只提供了二进制校核结果(即弹体贯穿或未发生贯穿),因此在利用“三步”法进行计算时并没有给出公式计算与实验结果的具体误差大小、以及各项设计参数,包括钢板厚度、混凝土墙厚度、钢板屈服强度、混凝土强度等对弹体贯穿速度的影响大小。
真实的飞机结构非常复杂,在评价飞机撞击安全壳体时首先需将飞机进行有效合理的简化。通常,视飞机机身为柔性构件(柔性弹体),飞机中的起落架、轮毂、发动机内部构件等可近似为刚性构件(刚性弹体)。在核工程安全壳设计中,以刚性构件为研究对象且忽略这些构件在撞击过程中自身的变形,所得到的设计结果偏于保守。本文中针对刚性弹体,提出基于能量法的钢板混凝土墙防贯穿计算方法,给出带对拉钢筋的双钢板混凝土墙的防贯穿实用计算公式,通过与已有实验数据以及飞机发动机撞击双钢板混凝土墙有限元分析结果进行对比分析,验证这一双钢板混凝土墙防贯穿实用计算方法的合理性和可行性。
1 机理分析和公式建立
依据能量法进行双钢板混凝土墙防贯穿计算方法的研究,弹体在贯穿带有对拉钢筋的双钢板混凝土墙时,能量的耗散可分为4 部分:墙体前钢板耗散的能量Ws1,混凝土耗散的能量Wc,后钢板耗散的能量Ws2,对拉钢筋耗散的能量Wt,根据能量守恒,则有:

式中:Ek为弹体撞击的初始动能,Ekr为弹体撞击后的剩余动能。如果考虑临界情况,即弹体刚好贯穿墙体,剩余速度恰好为0,剩余动能也为0,式(1)变为:

弹体撞击带对拉钢筋的双钢板混凝土墙的机理如图1 所示,其中,d为弹体直径,h为弹体头部长度,Hc为墙体混凝土部分厚度,Hs为钢板厚度。
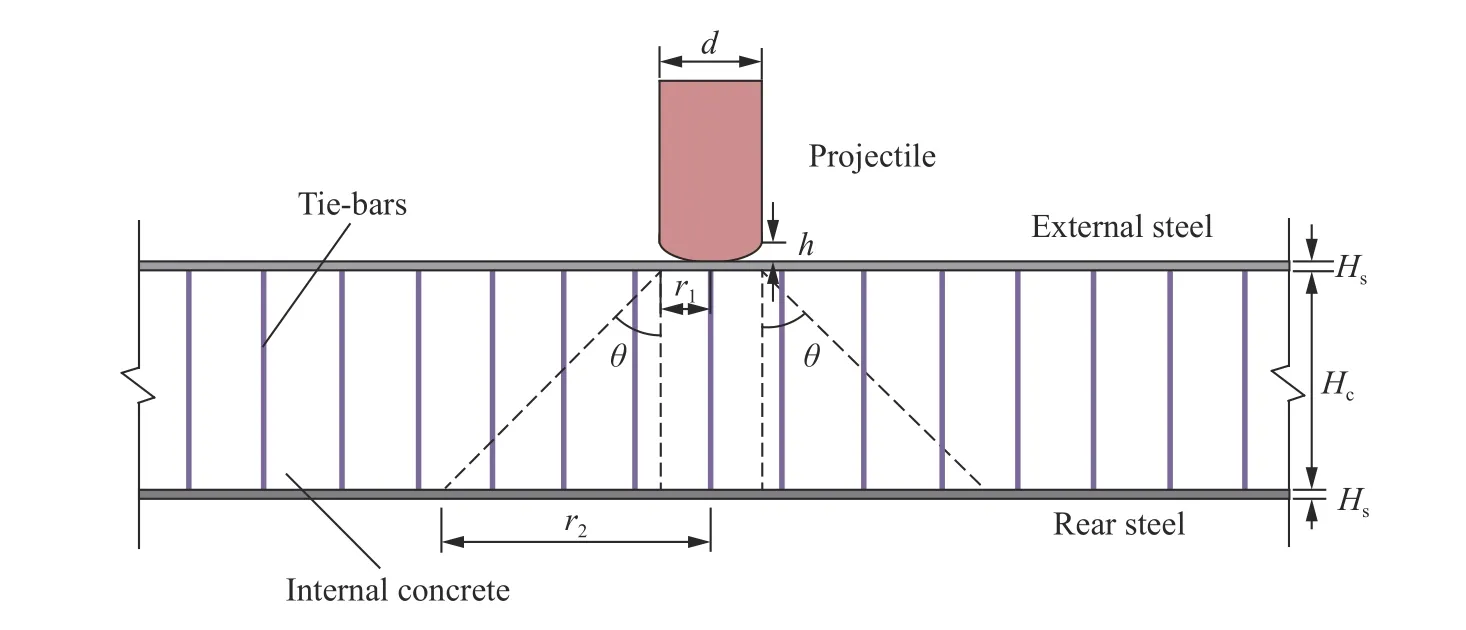
图1 弹体撞击带对拉钢筋的双钢板混凝土墙机理图Fig. 1 Mechanism diagram of missile impacting on SC wall with tied bars
弹体在撞击双钢板混凝土墙的过程中,由于双钢板混凝土墙外包钢板的约束作用,混凝土的飞溅和墙后的震塌可以略去不计,混凝土部分会形成一个“圆台体”,如图1 所示,该圆台体上底半径为r1,下底半径为r2。θ 为圆台体母线与竖直线的夹角。
下面对式(2)中4 部分耗散能量分别开展分析。
1.1 前钢板耗散的能量 Ws1
文献[11-12]利用空腔膨胀理论推导分析,分别给出了两种贯穿金属靶板的速度公式,两种贯穿速度公式基本一致,计算的贯穿速度结果相差10%,计算结果与相关实验进行对比分析,匹配程度较高。这两种贯穿速度公式没有弹体、靶体众多参数以及撞击速度的限制。参照文献[11]可以给出前钢板在弹体撞击发生贯穿时的耗能公式为:

1.2 混凝土耗散的能量 Wc
混凝土在贯穿过程中会形成一个圆台体[15-16],双钢板混凝土墙圆台体的形成机制是根据混凝土圆台体形成机制得来的,在双钢板混凝土墙中,由于对拉钢筋的作用,圆台体的θ 角会有所变化。圆台体的θ 角的大小与靶体厚度、弹体直径有关,根据文献[16],有:

根据文献[15],贯穿时混凝土墙的耗能可用下式表示:

1.3 后钢板耗散的能量 Ws2

1.4 对拉钢筋耗散的能量 Wt
双钢板之间的对拉钢筋对双钢板之间的圆台混凝土块起到了类似钢筋混凝土中的箍筋作用,由于对拉钢筋与混凝土共同工作,相比素混凝土,含对拉钢筋的混凝土抗冲击能力增强,从能量耗散的角度考虑,对拉钢筋耗散的能量不应忽略。在贯穿过程中,图1 圆台体及邻近区域的对拉钢筋与混凝土之间的黏结力受到破坏,混凝土圆台体随弹体整体向后移动,极限状态时横跨圆台体裂纹区的对拉钢筋发生拉屈破坏。对拉钢筋耗散的能量与对拉钢筋屈服强度、对拉钢筋横截面面积、对拉钢筋数量以及对拉钢筋的变形长度等因素相关,因此对拉钢筋耗散的能量可表示为:

式中:fd为对拉钢筋动力强化系数, σt为对拉钢筋屈服强度,At为单根对拉钢筋的横截面面积,le为对拉钢筋的有效变形长度,Nt为横跨圆台体裂缝上的对拉钢筋数量。
其中对拉钢筋的有效变形长度le:

2 防贯穿实用计算公式

当已知弹体以及钢板混凝土墙体各材料相关参数时,可采用钢板混凝土墙防撞击贯穿实用计算方法,对带对拉钢筋的核工程钢板混凝土墙体进行贯穿破坏快速评估,为钢板混凝土墙体的防贯穿初步设计提供指导。
3 与实验结果的对比分析
文献[18] 给出了弹体撞击双钢板混凝土墙的实验结果。实验弹体材料为钢材,弹体直径d=150 mm、长度300 mm,弹体头部为拱形,头部长度h=20 mm。弹体质量M1=40 kg,实验中弹体的初始撞击速度约为150 m/s。双钢板混凝土墙SCS-175-6T 及SCS-250-6T 大小均为2 m×2 m,墙体厚度Hc分别为175、250 mm,钢板的厚度Hs=6 mm。靶体模型中栓钉的直径dt=13 mm、长度为80 mm,栓钉间距s1=s2=150 mm,栓钉屈服强度 σt=345 MPa,栓钉抗拉强度设计值fy1=300 MPa。实验中SCS-175-6T 板的弹体初始撞击速度为152.4 m/s,SCS-250-6T 板的弹体撞击速度为147.7 m/s。SCS-175-6T 板撞击实验弹体贯穿了双钢板混凝土墙,弹体的剩余速度为33.9 m/s,而SCS-250-6T 板撞击实验的弹体未发生贯穿,弹体剩余速度为0。
由于弹体头部长度为20 mm,远小于弹体直径150 mm,因此N1和N2可以近似取值为1,第2 节计算公式中其他相关参数取值如表1 和表2 所示。该实验中栓钉引起的耗能可由对拉钢筋的耗能公式近似计算,前、后钢板、混凝土和栓钉的耗能以及剩余速度根据式(3)、(8)、(12)、(16)和(25)计算。根据公式计算得到的结果与实验结果对比如表3 所示,其中公式计算分别给出未考虑栓钉和考虑栓钉影响的两种结果。

表1 钢板计算参数Table 1 Calculation parameters of steel plate

表2 混凝土计算参数Table 2 Calculation parameters of concrete

表3 公式计算及实验结果Table 3 Formula calculation and test results
未考虑栓钉影响时,计算中仅考虑前钢板、混凝土和后钢板3 部分耗散的能量,由此得到工况SCS-175-6T 和工况SCS-250-6T 的剩余速度分别为41.5、0 m/s。2 种工况由公式计算得到的结果与实验结果在破坏形式上一致,剩余速度大小也比较接近。而实际实验中双钢板混凝土墙中虽没有布置对拉钢筋,但墙中设置了栓钉,在实际撞击实验中栓钉的存在也将耗散掉一部分能量,在使用公式计算时栓钉部分耗散的能量按对拉钢筋近似处理,剩余速度计算结果为34.3 m/s,可见,当考虑栓钉影响后,公式计算结果与实验结果更为接近。需要说明的是,文献[18]的实验中,栓钉并未通长布置,栓钉的锚固能力要弱于对拉钢筋,其耗能能力也弱于对拉钢筋,因此当考虑栓钉耗能时按公式计算的弹体剩余速度将略大于34.3 m/s。公式计算结果与实验结果的对比初步表明,本文中给出的双钢板混凝土墙防贯穿实用计算公式及剩余速度计算公式可以有效评估钢板混凝土墙体的贯穿反应。
4 与有限元计算结果的对比分析
由于以上对比只有2 个实验结果,为了避免偶然性,下面将采用动力有限元方法对钢板混凝土防撞击问题开展更广泛的模拟分析,通过有限元计算结果和公式计算结果做进一步对比分析。
4.1 有限元模型及其验证
为验证有限元模型在撞击计算中的有效性,参照文献[18] 中SCS-175-6T 和SCS-250-6T 的撞击实验建立有限元模型,弹体和双钢板混凝土墙的有限元模型如图2 所示。混凝土采用实体单元,钢板和栓钉分别采用壳单元和梁单元,栓钉和混凝土共节点,弹体与双钢板混凝土墙的接触采用自动单面接触,靶板四周在撞击方向上施加约束,混凝土墙体的有限元网格尺寸为25 mm×25 mm×25 mm,钢板的网格为25 mm×25 mm,弹体网格按25 mm 六面体划分。混凝土的本构模型采用MAT_CONCRETE_DAMAGE_REL3 模型(K&C 混凝土模型),混凝土相关参数见表2,混凝土泊松比取0.19,单元失效采用最大应变控制[19]。钢板、栓钉及弹体本构材料模型采用MAT_PLASTIC_KINEMATIC 随动硬化模型,应变率模型采用Cowper-Symonds 模型[19]。钢板、栓钉及弹体有限元模型相关参数见表4。

图2 弹体及弹-靶有限元模型(SCS-175-6T)Fig. 2 Overview of missile and missile-wall FE models (SCS-175-6T)

表4 有限元模型材料(MAT003)参数Table 4 Material parameters for FE models
当弹体的撞击速度为152.4 m/s 时,SCS-175-6T 板毁伤情况的数值计算结果和实验结果如图3 所示。从图3 可知,实验中SCS 板的破坏形态为贯穿,前后钢板均被破坏,出现孔洞,有限元模拟结果与实验结果一致。当弹体的撞击速度为147.7 m/s 时,SCS-250-6T 板的数值计算结果和实验结果如图4 所示。从图4 可以看出,靶板破坏形态为鼓包,前钢板完全被穿透,但是后钢板没有被撕碎,弹体完全侵入SCS 板中,在撞击中心位置有较大的鼓包形成,有限元模拟结果与实验结果一致。

图3 双钢板毁伤情况(SCS-175-6T)Fig. 3 Failure of steel plates (SCS-175-6T)

图4 双钢板毁伤情况(SCS-250-6T)Fig. 4 Failure of steel plates (SCS-250-6T)
对于弹体剩余速度和破坏形式,有限元计算结果和实验结果统一列于表5。SCS-175-6T 实验中弹体贯穿靶板后的剩余速度为33.9 m/s,而有限元模拟结果为28.7 m/s,这也表明有限元模型的耗能略大于实验模型的耗能,有限元模型的贯穿速度将略大于实验模型的贯穿速度,但两者比较接近。以上对比分析表明,在这两次撞击实验中,有限元模拟所得到的毁伤形式、剩余速度与实验结果均符合较好。说明所采用的有限元模型及相关计算参数是可信的。

表5 数值计算和实验结果Table 5 Numerical analysis and test results
4.2 有限元方法中临界贯穿速度的计算
为实现两种方法的对比,需要在有限元计算分析中,获得弹体撞击双钢板混凝土墙时的贯穿速度,若想精确地获得临界贯穿速度,达到既能贯穿,又使得弹体剩余速度恰好为0,需要繁冗的试算工作。本文处理的方法是,在撞击速度v作用下,未发生贯穿,将撞击速度再增大1 m/s 重新计算,如果能发生贯穿,则贯穿速度取v+1 m/s,这样贯穿速度精确到个位数。图5 为钝头弹分别以126、127 m/s速度撞击无对拉钢筋的双钢板混凝土墙时后钢板的毁伤情况。当撞击速度v=126 m/s 时,双钢板混凝土墙未发生贯穿,当v=127 m/s 时,发生了贯穿,由此确定此双钢板混凝土墙(SCS-175-4T)贯穿速度为127 m/s。图6 给出了撞击速度分别为126、127 m/s 时弹体的速度时程曲线,可以看出,撞击结束后,126 m/s 工况对应弹体的速度变为0,并有较小的反弹速度;127 m/s 工况对应弹体最后的剩余速度约为12.8 m/s。

图5 不同撞击速度下双钢板混凝土墙(SCS-175-4T)后钢板毁伤情况Fig. 5 Rear steel plates failure shape of SC walls at different impact velocities (SCS-175-4T)
根据文献[18] 的实验工况建立有限元模型。由于实验靶板内未配置对拉钢筋但设置了间距为150 mm 的栓钉,在使用公式计算时,分别按未考虑栓钉、考虑栓钉耗散能量进行计算。表6 给出了公式计算以及有限元计算得到的2 种工况的贯穿速度,2 种工况下,公式计算和有限元计算的偏差均小于5%,两者计算结果接近,而考虑栓钉影响时实用计算方法的预测精度可得到进一步改善。
在以上分析中给出了考虑和不考虑对拉钢筋/栓钉时贯穿速度预测结果的对比,为定量分析对拉钢筋对能量耗散的影响,研究中也开展了墙体各部分耗能所占比重的对比分析。利用实用公式计算得到工况SCS-175-6T 的前钢板、后钢板、混凝土、对拉钢筋4 部分的总耗能为413 820 J,其中,混凝土耗能为60 826 J,对拉钢筋耗能为17 946 J,混凝土和对拉钢筋耗能分别占总耗能的14.70%和4.34%;工况SCS-250-6T 的墙体总耗能为509 767 J,其中,混凝土耗能为145 991 J,对拉钢筋耗能为29 285 J,混凝土和对拉钢筋耗能分别占总耗能的28.64%和5.74%。分析结果表明,对于两种工况,双钢板的耗能基本不变;随着墙体厚度的增加,混凝土圆台体增大,对拉钢筋对耗能的占比随之增大。

图6 不同撞击速度下弹体的速度时程曲线(SCS-175-4T)Fig. 6 Velocity-time curves of the missile at different impact velocities (SCS-175-4T)

表6 双钢板混凝土墙贯穿速度对比Table 6 Comparison of perforation velocities of SC walls
4.3 飞机发动机撞击双钢板混凝土墙分析
以上工况中的弹体直径小、质量小,对于大直径、大质量的飞机发动机,所给出的双钢板混凝土墙防贯穿计算公式是否合理可行,需要进一步分析。商用飞机发动机主要由机匣、涡扇叶片、燃烧室、高压压气机、高压涡轮等构件组成。由于发动机构造复杂,在评价飞机发动机撞击核安全壳时可将发动机进行合理简化,本文在有限元法计算中将飞机发动机分别简化为实心圆柱体和前端封闭的圆柱壳两种弹体进行模拟,通过变化发动机类型、发动机质量、发动机直径、混凝土厚度参数,将公式计算的贯穿速度与有限元计算结果进行对比,共考虑了10 种计算工况,图7 和图8 分别为工况C5、C6 的飞机发动机有限元模型以及工况C6 的有限元模型,其他工况的有限元模型与工况C5、C6 相似。
10 种工况的混凝土有限元模型均采用实体单元,钢板和对拉钢筋分别采用壳单元和梁单元,对拉钢筋与混凝土单元耦合共同受力,弹体与双钢板混凝土墙的接触采用自动单面接触模式,靶板四周在撞击方向上施加约束。考虑到网格尺寸大小对计算结果的影响,在保持与4.1 节有限元模型一致性的基础上,同时为保证各工况的计算效率,10 种工况中除工况C1、C2 墙体混凝土和对应钢板的网格尺寸均按25 mm 划分外,其余工况混凝土和对应钢板部分的网格尺寸在模型中部区域控制在25 mm 左右,周边网格尺寸适当增大。所有发动机有限元网格大小均按25 mm 六面体划分。
对拉钢筋本构模型采用MAT_PLASTIC_KINEMATIC 随动硬化模型[19]。发动机本构模型采用MAT_RIGID 刚性材料模型[19],其余有限元模型材料本构和参数同4.1 节。
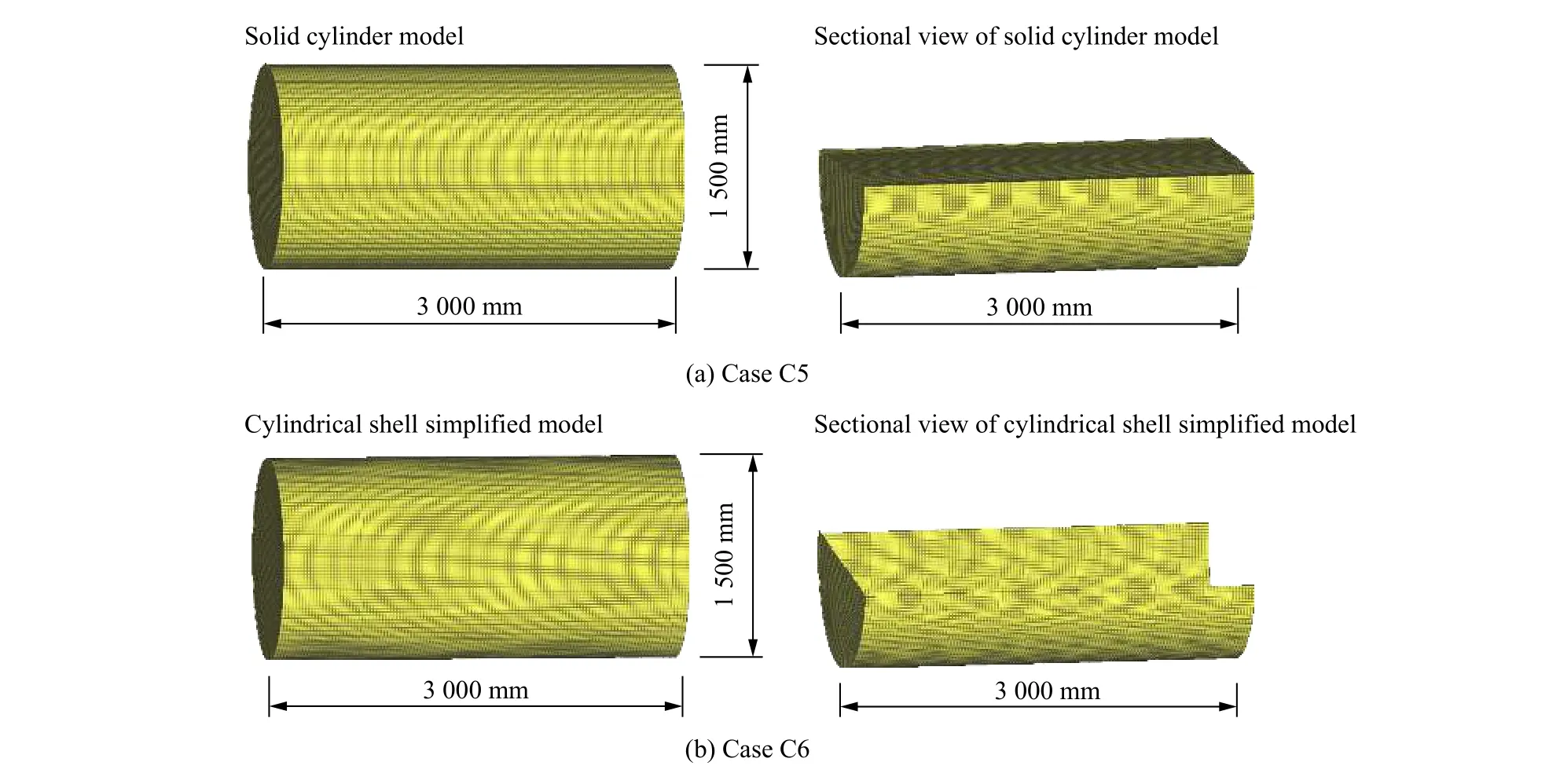
图7 工况C 5、C6 飞机发动机有限元模型Fig. 7 Aircraft engine FE models of cases C5 and C6
10 种工况对应的部分计算参数见表7,其余计算参数为:由于弹体模型均为平头弹,故弹体头部长度h=0,圆柱壳弹体厚度均为10 mm;混凝土的抗压强度为50 MPa,抗拉强度设计值为1.9 MPa,密度2 350 kg/m3,对拉钢筋间距200 mm、直径20 mm、屈服强度345 MPa、抗拉强度设计值300 MPa,根据文献[17],对拉钢筋外形系数α=0.16、对拉钢筋锚固长度修正系数ζ=0.6、断裂应变 εst取0.3[20],根据文献[21-22],对拉钢筋动力强化系数fd取1.2,钢板的厚度为10 mm、屈服强度307 MPa、密度7 850 kg/m3、弹性模量210 GPa。
表7 中给出了飞机发动机撞击带对拉钢筋双钢板混凝土墙的贯穿速度。从表中可以看出,公式的计算结果与有限元分析的结果较为接近,除工况C5 偏差略超10%以外,其余工况偏差绝对值均在8%以内;对于有限元分析得出的贯穿速度,采用前端封闭的圆柱壳发动机模型得到的贯穿速度要高于实心圆柱体发动机模型的计算结果;实用计算公式得到的贯穿速度与前端封闭的圆柱壳发动机模型给出的速度计算偏差小于5%。弹体的贯穿速度随着弹体质量的增大而降低。以上结果表明,对于飞机发动机,本文中给出的带对拉钢筋双钢板混凝土墙的防贯穿公式是合理可信的,该公式可用于双钢板混凝土墙的防贯穿设计以及对核工程双钢板混凝土墙开展安全评估。

图8 工况C6 有限元模型Fig. 8 FE model of case C6
目前国际核电建设已进入第三代发展时期,具有代表性的第三代核电技术AP1000[23]核电机组,其安全壳采用双钢板混凝土结构。参照AP1000 核电机组及我国的某核电站安全壳结构形式建立双钢板混凝土墙模型。双钢板混凝土墙厚1.1 m、钢板厚20 mm、钢板屈服强度345 MPa、混凝土抗压强度55 MPa,对拉钢筋的直径为20 mm、屈服强度为400 MPa、间距为475 mm。以Boeing 767-200ER 的发动机CF6-80C2[24-25]为对象,该发动机单个质量4.35 t、直径2.5 m、长度6.0 m。对于CF6-80C2 发动机,利用本文中提出的防贯穿计算公式计算得到的结果是:若以Boeing 767-200ER 的发动机CF6-80C2 撞击上述双钢板混凝土墙体,发动机贯穿速度为205.6 m/s,大于现有飞机坠毁记录以及目前民航飞机的起飞降落速度要求,可以看出该核电站双钢板混凝土墙对于防飞机发动机贯穿是安全的。
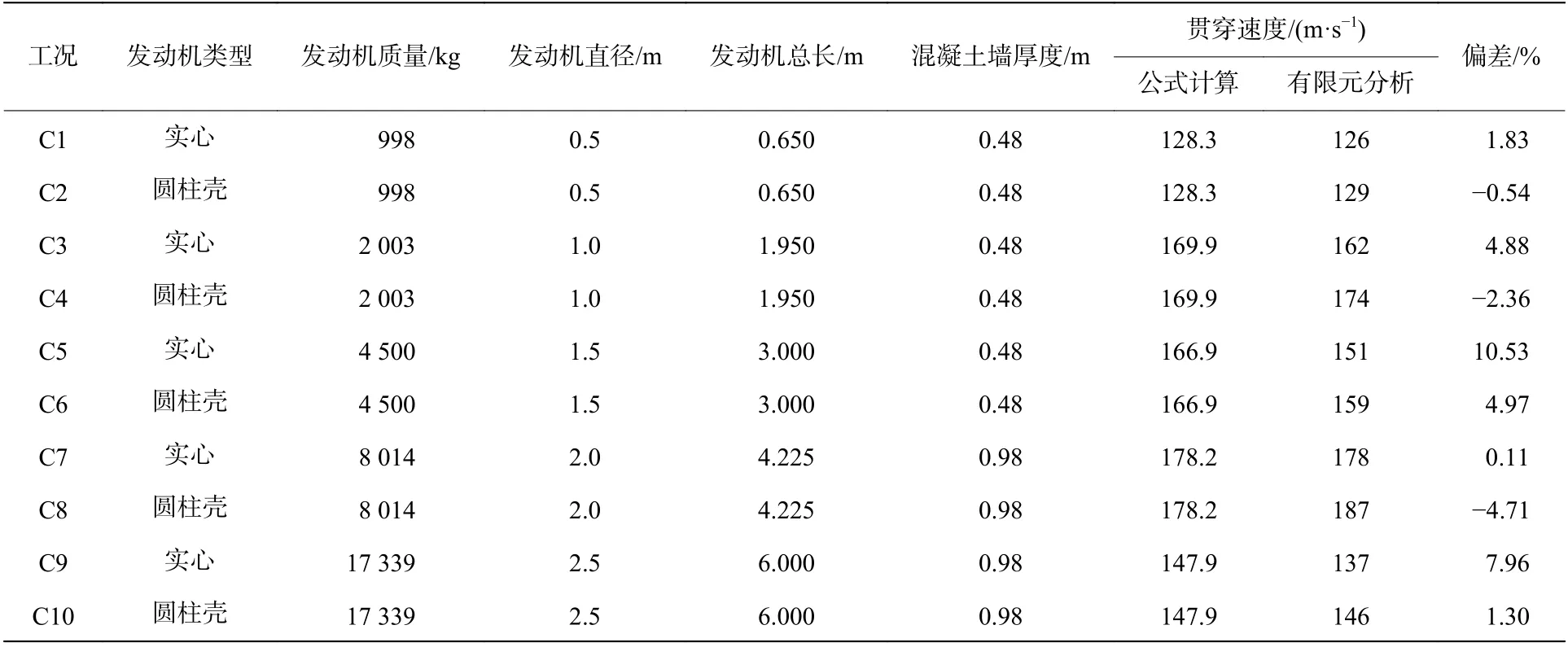
表7 飞机发动机撞击双钢板混凝土墙的贯穿速度对比Table 7 Comparison of perforation velocities for SC walls subjected to an aircraft engine
5 结 论
通过分析刚性弹体撞击双钢板混凝土墙的贯穿机制,提出了一种防贯穿实用计算公式,与实验以及有限元模型进行了对比,得出主要结论如下:
(1)基于能量法研究了双钢板混凝土墙防贯穿计算方法,将弹体贯穿双钢板混凝土墙的能量耗散分为前钢板、后钢板、混凝土以及对拉钢筋耗散的能量4 部分,提出了基于能量法的钢板混凝土墙防贯穿实用计算公式。
(2)基于防贯穿计算公式的计算结果与实验及有限元分析的结果相比,除个别工况计算结果偏差略超10%外,其余均在10%以内,说明本文给出的计算公式是合理可信的,能有效评估双钢板混凝土墙的贯穿破坏和进行相关设计。
(3)在质量不变的条件下,飞机发动机可简化为实心圆柱体或者前端封闭的圆柱壳平头弹,这样的简化对采用有限元方法分析双钢板混凝土墙抗飞机发动机撞击贯穿速度的计算结果影响不大,采用前端封闭的圆柱壳发动机模型获得的贯穿速度略大于实心圆柱体模型,弹体的贯穿速度随着弹体质量的增大而降低。
