球形颗粒遮弹层对高速侵彻弹体的作用机理*

郭 虎，何丽灵，陈小伟，陈 刚，李继承

（1. 中国工程物理研究院总体工程研究所，四川 绵阳 621999；2. 工程材料与结构冲击振动四川省重点实验室，四川 绵阳 621999；3. 北京理工大学前沿交叉科学研究院，北京 100081；4. 北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

在地面目标“发现即被摧毁”的现代战争环境下，核心价值目标纷纷转移至地下，而钻地弹是攻击此类目标的利器。随材料与结构设计技术以及运载技术的发展，钻地弹能达到更高的侵彻速度，具备攻击埋深更大的地下目标能力[1]。钻地弹的快速发展对地下工事的防御强度提出更高要求。除增大埋深外，覆遮弹层是增强地下工事防御强度较快速、简便和有效的方法。遮弹原理主要有被动式、反应式和主动式。

被动式遮弹层是本文主要关注遮弹层类型，其通常具备优良的抗侵彻性能、高可靠度、便于设计与施工、耐久性强、易修复、不给其他防护措施带来负面效应以及造价低廉等特点[2]。采用新材料或新结构增大遮弹层强度，或引入二次碰撞机制偏转弹丸弹道以减小有效侵深，是被动式遮弹层的基本思想[3]。块石、钢纤维/钢球混凝土、刚玉/陶瓷、强度为150～200 MPa 的超高强混凝土[4]等是遮弹层主要制作材料。三角形中空梁、混凝土栅板、含钢球的钢纤维混凝土、钢板-钢纤维混凝土、双层表面异型偏航复合遮弹层等是被动式遮弹层常见结构形式[5]。带球面结构在遮弹层中较为常见，目的是引入弹体不对称载荷，从而诱使弹体弯曲变形，偏转弹道。

数值试验是低成本研究弹靶侵彻响应的有效手段。周布奎等[6]假设弹体和刚玉球为刚体，数值分析单层密排刚玉球埋深、球直径、弹着靶位置、球约束边界等对正侵彻时弹靶响应影响，得到球直径越大、埋深越浅、边界约束越强，遮弹效果越好的定性结论。试验也获得了类似的研究结论[3]。弹体与刚玉球的刚性假设仅能考虑动能变化而无法计及两者变形与耗能，这与实际存在偏差；同时，实际着靶时弹体很难保持理想正侵彻姿态。穆朝民等[7]将弹体还原为可变形弹，长杆弹斜侵彻块石遮弹层的数值分析显示，弹体发生结构弯曲，弹道偏转明显。事实上，斜侵彻姿态引入的弯曲等结构变形与弹靶响应相耦合，刚性弹假设将无法分析该问题。

在弹靶响应数值分析中，与弹体相比，靶尺寸常大一个数量级以上，靶体响应与弹靶接触计算将耗费大部分计算时间，当弹体运动和变形为关注重点时，将大大降低分析效率。弹靶分离方法建立靶对弹体阻力的表征模型，并将该等效阻力作为载荷边界施加在弹体外表面，从而不需建立靶数值模型就可分析与靶作用时弹体的运动和变形，省去了靶响应计算时间，大大提高了计算效率[8-16]。合理表征靶对弹体侵彻阻力是模拟弹体运动与变形的前提。本文将采用相同方法开展分析研究。

针对弹体侵彻脆性靶问题，从侵彻隧道至靶自由表面，靶体依次呈现粉碎破坏、开裂破坏及弹性变形形态[15]。基于球形动态空腔膨胀理论，可将弹体表面压力表示为靶动态抗压强度与弹体侵彻速度的函数。当靶尺寸足够大且弹体侵彻姿态与理想正侵彻偏离较小时，如侵彻斜角在10°以内、攻角在1°以内，着靶面对弹体影响可忽略[11]。当侵彻斜角增大或靶尺寸过小，自由边界将削弱靶对弹体的约束，这称为靶自由面效应。弹体表面至自由面距离成为影响自由面效应的重要参数。常采用折减系数表征自由面效应对弹体表面压力的改变，而折减系数可表征为有限靶介质与无限靶介质中弹体表面压力之比[9,12]。

基于上述研究，本文将采用弹靶分离计算方法分析弹体斜侵彻内埋硬质球形颗粒的有限大高强混凝土靶响应，考虑颗粒的位置、尺寸及强度影响，研究球形颗粒遮弹层对弹体变形及轨迹影响的机理。

1 含球形颗粒有限大高强混凝土靶对弹体等效侵彻阻力表征

含球形颗粒有限大高强混凝土靶有以下内涵：

(1)靶基体材料为高强混凝土；

(2)尺寸有限大，即需考虑靶所有自由面影响；

(3)内含与靶强度不同的球形颗粒。

针对半无限高强混凝土靶，可采用球形动态空腔膨胀模型表征其侵彻阻力[4,15]，即弹体表面压力σn为：

靶自由面对弹体表面压力的影响采用衰减函数表征，则弹体表面压力修正为式（3）的右式与衰减函数的乘积[9,12,15]。在半无限混凝土靶中，从侵彻隧道向外可分为4 个区域：空腔区、破碎区、弹性区和无扰动区，如图1 所示。空腔半径为r'，破碎区最大半径为rp，弹性区最大半径为relas。若rd表示弹体表面质点与自由面的距离，如图2 所示，当rd≤rp时，靶自由面位于破碎区内，靶对弹体无侧向约束，即自由面衰减函数取值为0；当rd＞rp时，衰减函数定义为有限与无限大靶介质内弹体表面径向应力之比[9,12]。基于球形空腔膨胀理论，衰减函数表达式为：

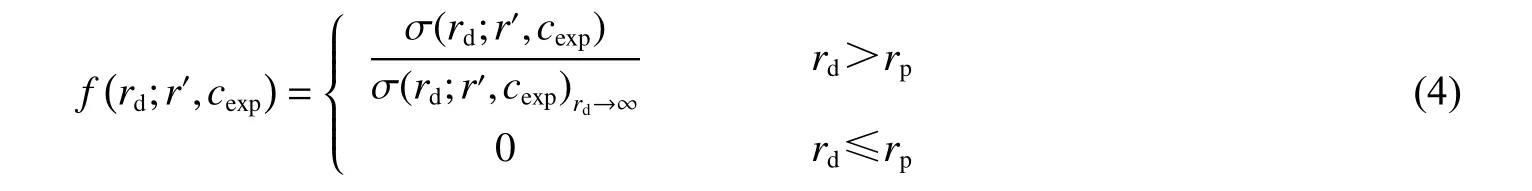
式中：σ 为介质内空腔表面径向应力，与rd、r'和cexp有关。鉴于靶材可压缩性对深侵彻弹体阻力仅二阶影响[17]，且考虑压缩性将大大增加空腔表面应力求解难度[9]，本文中假设靶材不可压缩。采用Mohr-Coulomb 屈服准则描述靶材力学行为，则当rd＞rp时，有限大靶介质内空腔表面径向应力为[10-12,15]：

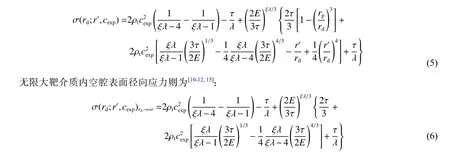
式中：ξ、λ 和τ 均为靶材的材料常数，λ 为混凝土强度相对静水压力的变化率，而τ 为静水压力为零时混凝土强度，ξ 表征混凝土剪切强度随压力的变化，ξ=6/(3+2λ)；E为混凝土材料弹性模量。由破碎区与弹性区的连续条件，可得rp=r'[2E/(3τ)]1/3。λ=0.52，1.023 时[12,15]，混凝土自由面衰减函数随弹体表面质点离自由面距离变化关系见图3，可见，随侵彻速度升高，自由面影响区域增大。当弹体表面质点与自由面距离

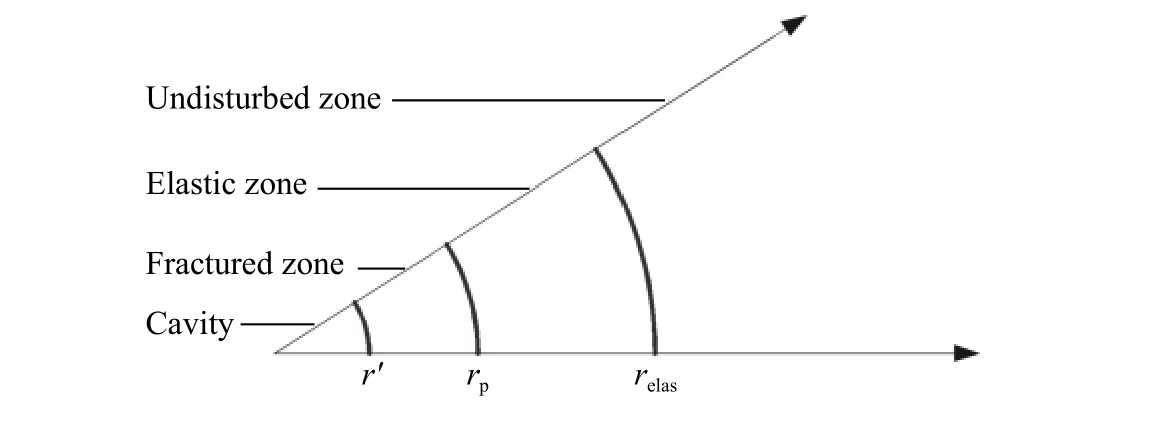
图1 侵彻过程中混凝土靶空腔膨胀响应分区Fig. 1 Partition of a concrete target during penetration based on the dynamic cavity expansion model

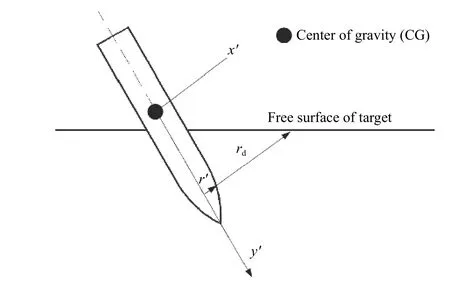
图2 非正侵彻弹体与靶自由面位置示意图Fig. 2 Scheme of a projectile obliquelypenetrating into a target

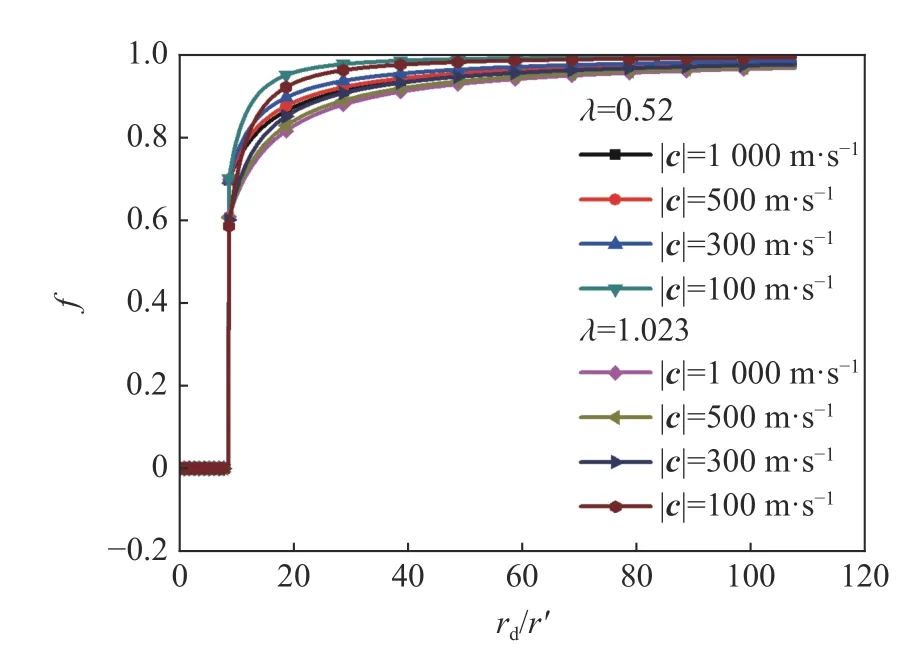
图3 自由面衰减函数随弹体表面质点离自由面距离的变化Fig. 3 Change of the discount factor of free-surface effect with the distance from the target free surface to the projectile surface

针对有限大靶，存在数个自由边界，此时rd应为弹体表面质点与靶所有自由面距离的最小值。计及自由面衰减效应的影响，将式（3）的右式与式（4）相乘，得修正后弹体表面压力为[9,12,15]：

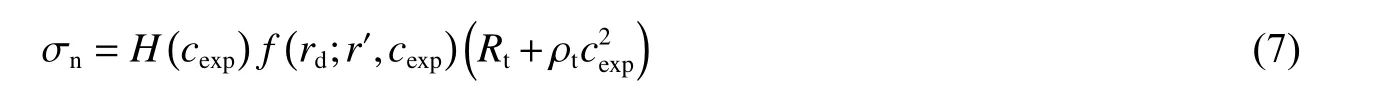
假设内埋球形颗粒位置始终保持不变，且任意时刻颗粒区域内均具备同等抗侵彻能力（即不考虑颗粒被穿透破碎后弹体再入破碎区问题），并将任意空腔膨胀速度下的颗粒阻力与无颗粒时阻力之比折算为常系数f1，则：

式中：g1为颗粒与混凝土对弹侵彻阻力之比。

将式（7）的右式与式（8）相乘，得考虑颗粒强度差异、靶自由边界等影响，含球形颗粒有限大高强混凝土靶对弹体等效表面压力的表达式，即：

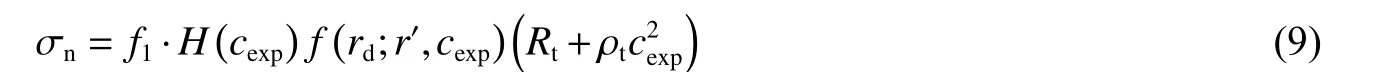
此时，侵彻含球形颗粒有限大高强混凝土靶时，弹体响应分析只需将式（9）表示的压力施加在弹体表面，而不需建立靶体的数值计算模型。本文中将二次开发有限元商业软件，依照图4 流程施加弹体表面载荷（式（9））。

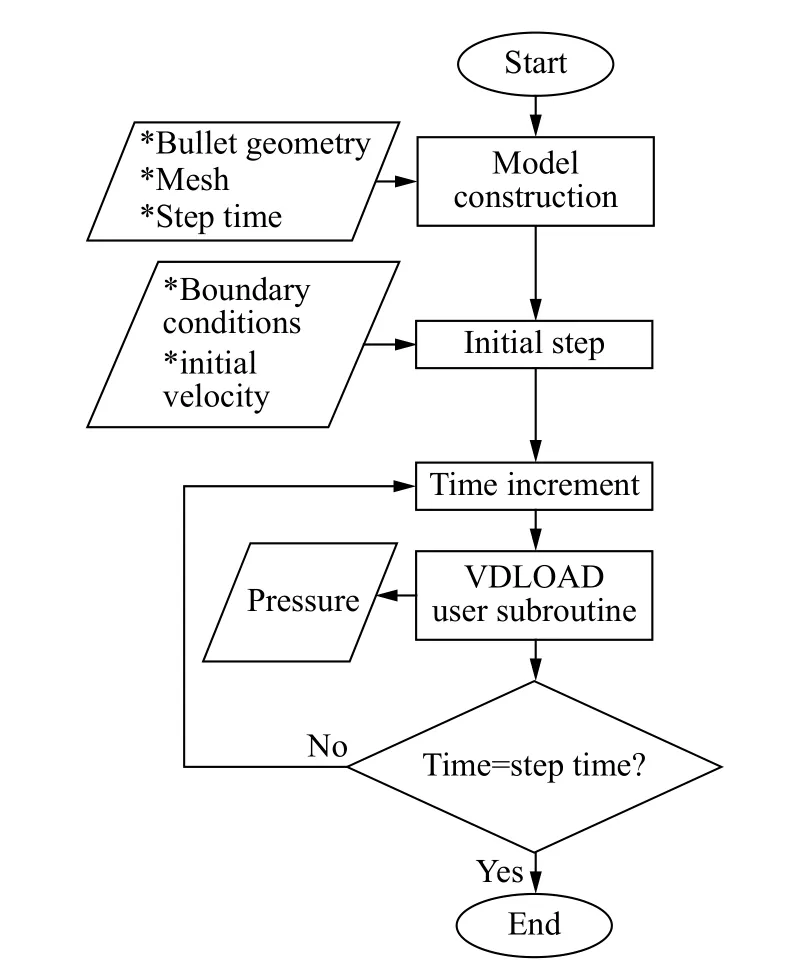
图4 有限元软件中弹体表面压力载荷边界施加流程图[16]Fig. 4 Flow chart of pressure on projectile surface in FEM software[16]

2 高强混凝土内硬质球形颗粒对可变形弹变形和运动的影响

2.1 弹靶描述

考察尖卵形弹体斜侵彻内埋硬质球形颗粒高强混凝土靶问题，本文中研究的弹体以及混凝土的材料性能与Frew 等[18]的试验一致。混凝土靶为带斜面的长方体，着靶面为斜面，倾角为30°，最长边长1 020 mm，后靶面为边长510 mm的正方形，见图5。混凝土靶密度为2 400 kg/m3，无约束抗压强度为63.8 MPa，动态抗压强度Rt为925 MPa，内埋硬质球形颗粒强度比混凝土强度高，如刚玉、特种陶瓷、高强钢等，g1＞1。弹体实心，直径为7.1 mm，长径比为10，弹头尖卵形，弹头轮廓母线的曲率半径和弹径之比（CRH）为3。弹体材料为AerMet100 钢，采用Johnson-Cook 模型表征其力学行为，参考应变率为1 s−1，参考应变率下，强度参数A=1 500 MPa，应变硬化相关的强度参数B=500 MPa，应变强化指数n=0.53，应变率强化指数φ=0.014，温度软化效应系数m=1.13，参考温度取298 K，材料熔化温度取1813 K。靶最长边与x轴平行，且弹体着靶点坐标为(0, 0,0)，见图5。需要说明的是，图5 中坐标系仅表示坐标轴平行方向，坐标原点在靶斜面的中心。数值分析中对靶体阻力采用式（9）表征，靶有限元模型未参与计算。结果中显示靶体仅为更形象地说明弹靶相对位置。

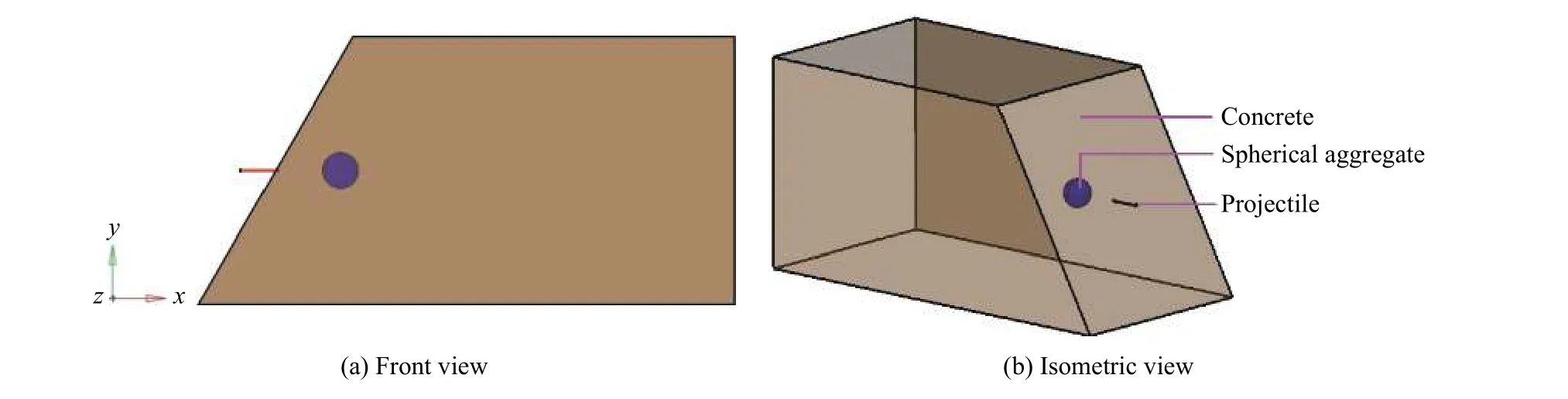
图5 弹靶示意图Fig. 5 Scheme of the projectile and target for oblique penetration

除侵深外，弹道偏转也将影响弹体攻击效率。采用弹体转动角度表征弹道偏转程度，其计算方法见图6。图中CD表示着靶时刻弹体的位置，假设弹体无攻角，或攻角较小，控制在5°以内，弹体在平行纸面的平面（即xy平面）内运动，则弹尖C坐标为(0, 0)，弹尾D坐标为(−lp,0)，其中lp为弹体长度。不考虑垂直纸面的运动，在t′时刻，弹 体 运 动 至C′D′ 位 置， 其 坐 标 分 别 为C′(uC,vC)和D′(uD−lp,vD)。其中，u和v分别为x、y方向的位移，下标C、D分别标识弹尖或弹尾参量。此时弹体转动角度α 可表征为：

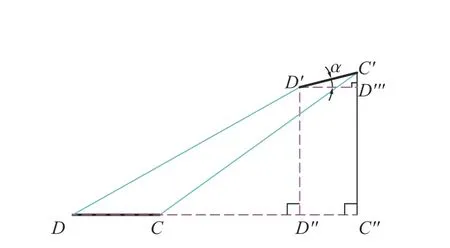
图6 弹体转动角度Fig. 6 Rotation angle of the projectile

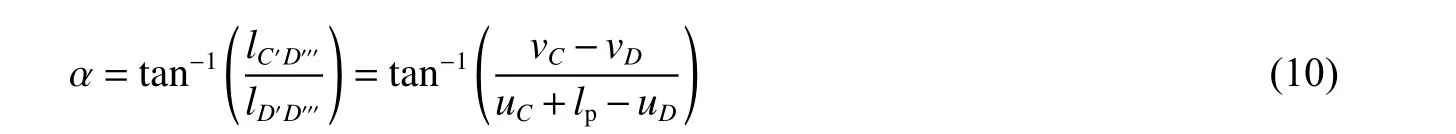
式中：lC'D'''为点C'至点D'''的距离，lD'D'''为点D'至点D'''的距离。需要说明的是，式（10）计算的弹体转动角度耦合了弹体结构弯曲等变形引起的角度变化。

2.2 硬质球形颗粒位置及强度的影响

为分析硬质球形颗粒的影响，需选择对比参考工况。本文中选择弹体以斜角30°、下攻角1°、右攻角1.5°和撞击速度1 266 m/s 侵彻未埋球形颗粒的高强混凝土为参考工况。后文如无特殊说明，参考工况均指该工况。

鉴于参考工况为斜侵彻，取弹体运动轨迹长度为名义侵彻深度。与同速度时正侵彻弹体侵彻深度试验结果对比显示，模型预测侵深336 mm 与试验结果379 mm[18]偏差约−11%，吻合良好。这说明本文计算模型具有合理性。

选取硬质球体半径35.5 mm（5 倍弹径），强度比例系数g1=2。改变球体嵌埋位置，分析弹体响应，并与参考工况对比，研究球体嵌埋位置对弹体变形及轨迹影响。考察5 个嵌埋位置，球心分别位于(50, 0,0)、(100, 0, 0)、(200, 0, 0)、(200, 25, 0)和(200, 50, 0)，除有球体嵌埋外，其余弹靶参数与参考工况相同。类似地，改变嵌埋在(200, 0, 0)处球体强度，g1=4，考察球体强度对弹体变形及轨迹影响。

弹体的头尖部位移、路程、偏转角度及变形情况与参考工况对比见表1。可见，弹体主要在xy平面运动，因此可以忽略弹体z向运动。此时，弹体有效侵彻深度（depth of penetration,DOP）定义为弹尖运动轨迹在靶面法线方向的投影长度，见图7。由图7、表1 可知，讨论位置的嵌埋硬质球体均能降低弹体有效侵深。g1=2 时，有效侵深减少量在5%至35%之间，最大减少量出现在嵌埋球心位于(200, 0, 0)处，硬质球形颗粒对有效侵深的折减效果不随颗粒埋深增加而单调变化：嵌埋硬质球形颗粒可能使弹体向着靶面偏转，如图7 中W-3 和W-6 所示，有利于目标防护；也可能向有效侵彻深度方向偏转，如W-1和W-5，可能对目标构成更大威胁；还可能几乎不改变弹体运动方向，如W-2 和W-4。对比W-3 与W-6 可知，同一位置嵌埋相同球体，强度越高，侵深折减越大，如图7 和表1 所示。下文将进一步分析能量、载荷等以认识嵌埋球形颗粒折减弹体有效侵深的机理及影响因素。

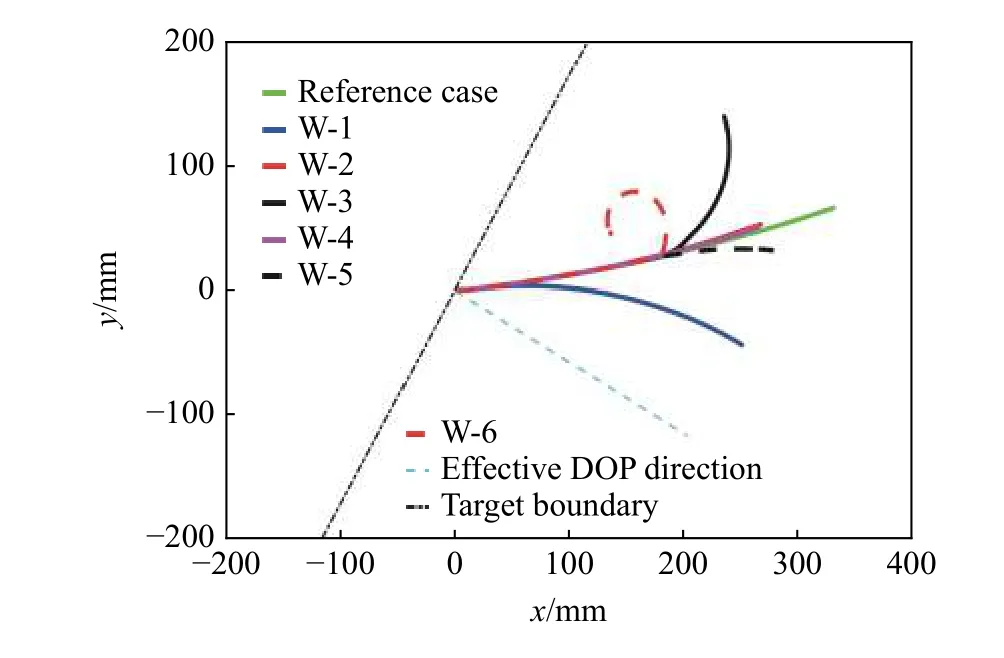
图7 颗粒位置及强度变化时弹尖xy 平面内运动轨迹Fig. 7 Trajectory of projectile nose tip in xy plane with variation of location and strength of aggregate

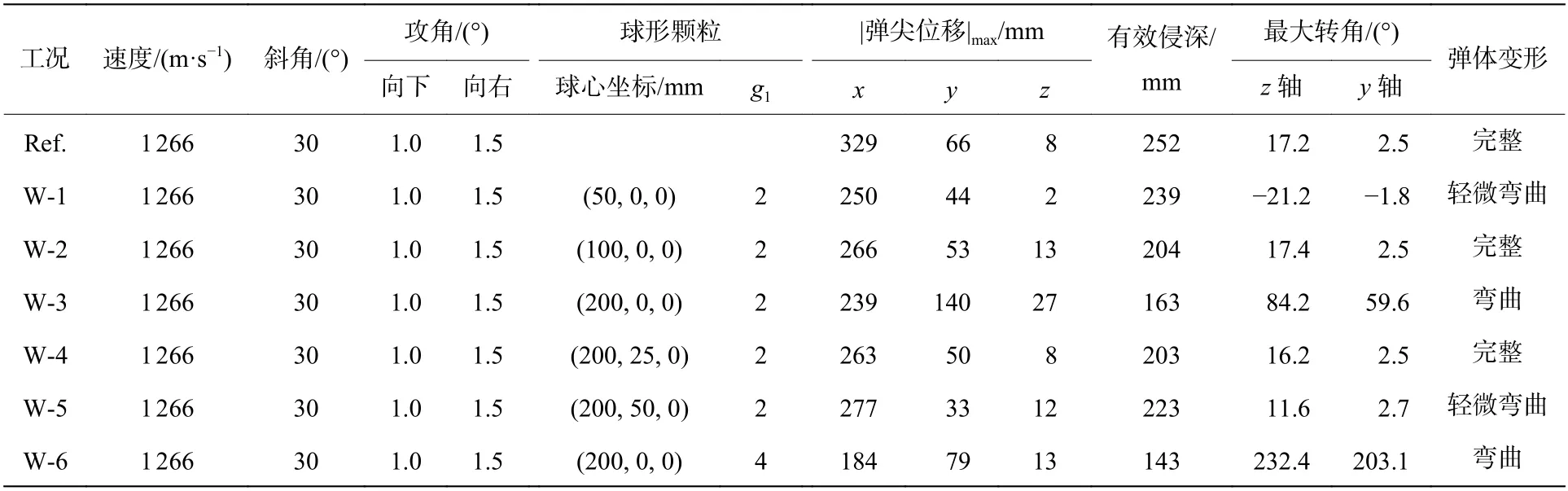
表1 半径为5 倍弹径球体嵌埋位置及强度对弹体运动和变形的影响Table 1 Movement and deformation of the projectile with the location and strength variation of the aggregate whose radius is 5 times of the projectile diameter

侵彻后弹体局部出现塑性变形，且呈现不同程度的结构弯曲变形，见图8。从能量角度出发，弹靶侵彻问题的总能量等于弹体初始动能，其主要转化为弹体变形内能以及靶变形与破坏消耗能量。针对讨论工况，图9 展示了弹体内能占总能量比值，图中γ 为弹体内能与总能量之比。可见，弹体内能占比通常在5%以内，即使弹体明显弯曲（W-6），其内能占比最大值也仅不到6%，因此弹体内能耗散不是弹体有效侵深降低的主要原因。

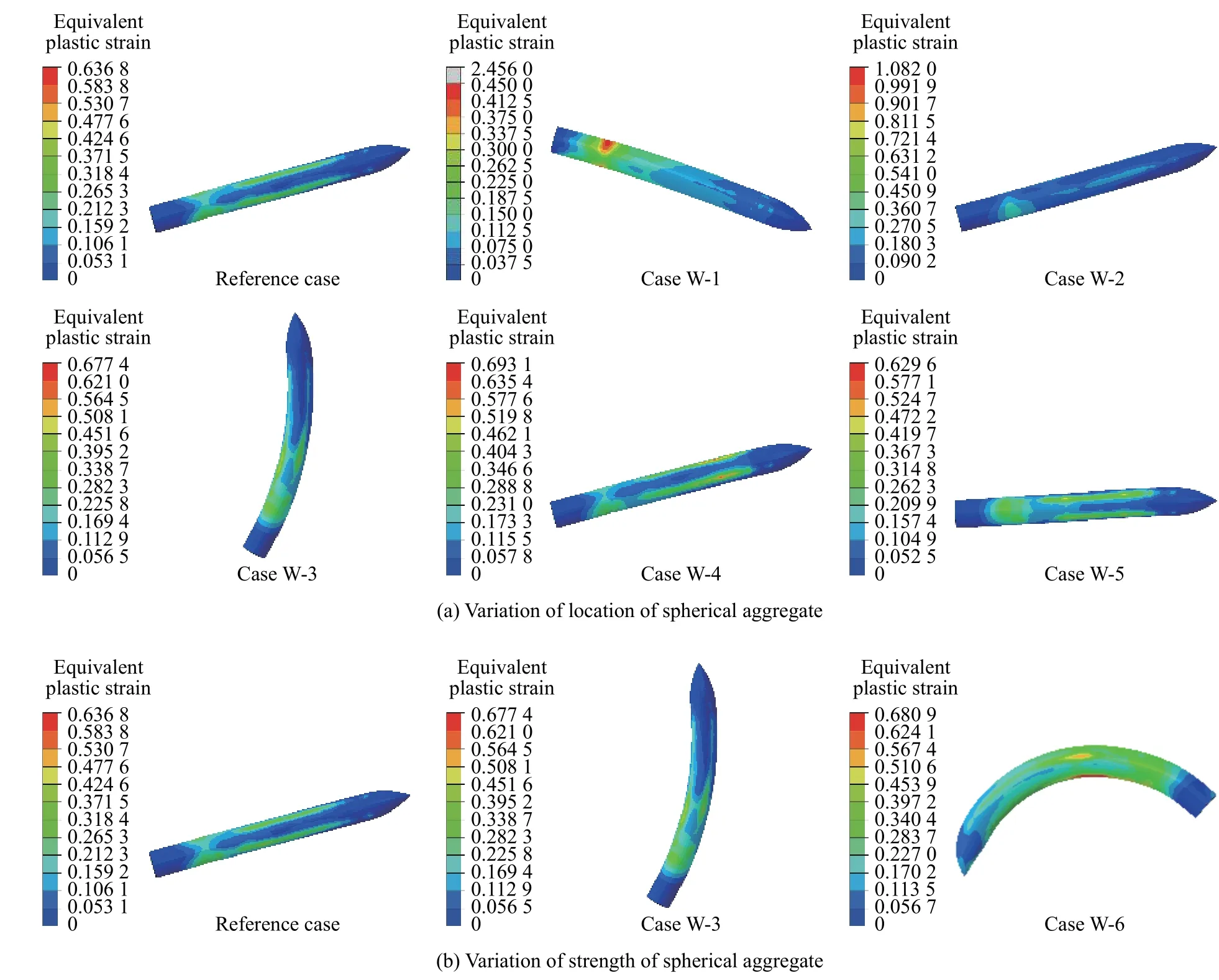
图8 侵彻后弹体的等效塑性应变分布及形状对比Fig. 8 Equivalent plastic strain distribution and deformation of projectile after penetration

基于动力学与运动学分析，降低弹体有效侵深的途径有两个：一是增大侵彻阻力；二是使弹道向着靶面偏转。

硬质球形颗粒将增大靶体局部强度。若弹体运动方向保持不变，弹体与硬质颗粒相互作用距离越大，增加的靶侵彻阻力对侵深的折减越大。图10 展示了6 种工况的弹体与球形颗粒作用时典型时刻相对位置，各分图左图为弹体与颗粒开始作用时刻两者相对位置，右图为弹体与颗粒相互作用距离最大时两者相对位置。可见，W-1 弹体与颗粒可达的瞬时作用最大距离与颗粒直径相当，较其他5 种工况都大，W-3 与W-6 可达的瞬时作用最大距离最短。然而，结合表1 可知，有效侵深折减与球形颗粒和弹体作用距离长短并不正相关。这说明弹道偏转在有效侵深折减中扮演重要角色。

若弹体有结构变形，弹体壳体将承受部分侵彻阻力。弹体质心x向侵彻阻力见图11(a)，其表征了弹体壳体与头部侵彻阻力合力的x向分量。显然，针对仅改变球形颗粒位置的W-1 至W-5 这5 个工况，尽管颗粒引起的x向侵彻阻力增加出现的时间各不相同，但其阻力增加持续时长及增加幅值差别较小，推断5 个工况的侵彻阻力增加引起的侵深减小量应差别不大。然而事实并非如此。进一步分析显示，弹体质心的x向阻力仅能表征质心平动，而不能表征弹体绕质心的转动。侵彻过程中作用在弹体上的非零力矩，将可能使弹体产生刚体转动或（和）结构弯曲，从而导致弹道偏转。这说明弹体刚体转动和结构弯曲应是弹体有效侵深折减的重要原因。

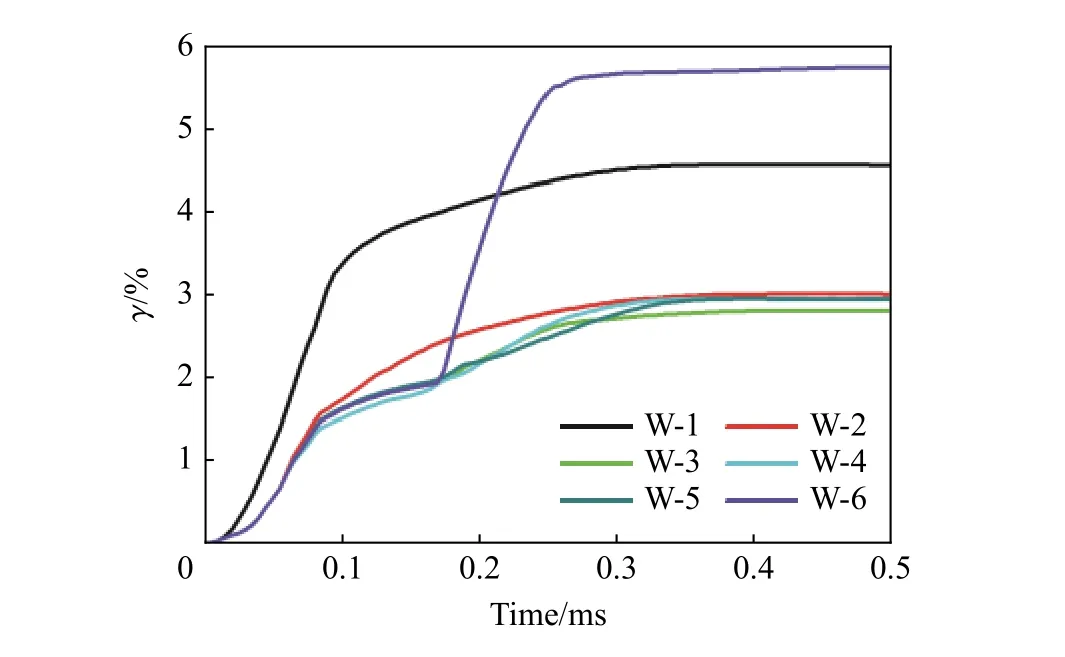
图9 不同工况下弹体内能占总能量比值随时间的变化Fig. 9 Change of internal energy-to-total-energy ratio of the projectile with time in different cases

图10 不同工况下弹与球形颗粒作用位置及距离Fig. 10 Interaction distance between projectile and aggregate in different cases

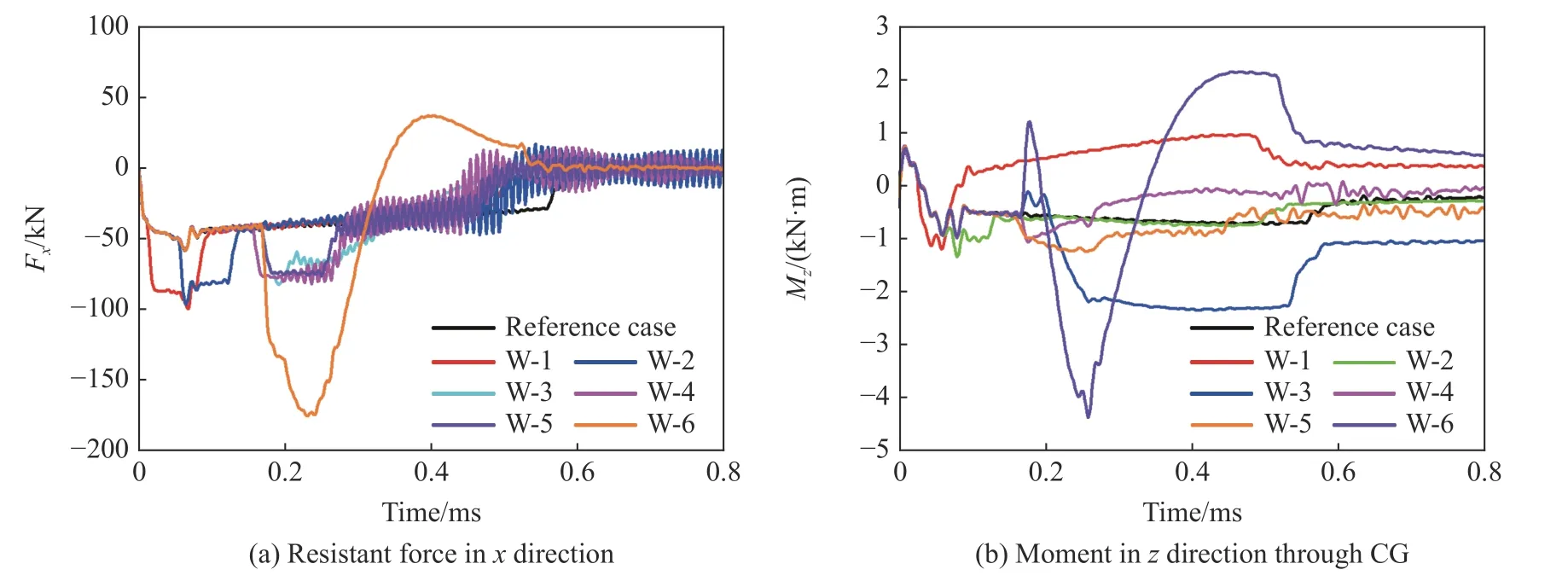
图11 颗粒位置及强度变化时，弹体质心x 向阻力及过质心z 向力矩的时间历程（125 kHz 低通滤波）Fig. 11 Time histories of x-directional resistant force and z-directional moment through projectile mass center for projectile with variation of location and strength of spherical aggregate(filtered by low pass filter with cutoff frequency 125 kHz)

引起弹道偏转的根本原因是载荷关于弹体轴线不对称，有非零力矩作用在弹体上。不对称载荷激发源主要分为4 类：（1）靶强度分布不均；（2）靶自由面效应；（3）弹体形状不对称，如头部偏磨、结构弯曲等；（4）弹体的非正侵彻姿态。本文参考工况不对称载荷激发源主要为（2）、（3）和（4），主要发生在侵彻初期；而嵌埋硬质球形颗粒的混凝土靶侵彻问题包含上述所有不对称载荷激发源，几乎贯穿整个侵彻过程。在弹体侵彻不同时刻，各激发源相互竞争，综合反映为弹体过质心合力矩的z向分量变化，见图11(b)。需要说明的是，过质心作用在弹体的合力矩z向分量指合力矩过质心绕z轴的力矩分量，其余方向力矩分量的定义以此类推。

在参考工况中，典型时刻弹靶位置及弹体变形见图12。撞靶初期，弹体非正侵彻姿态与自由面效应占主导作用，而后结构弯曲进一步加剧弹体载荷不对称。在侵彻后期，结构弯曲是产生弹体非零合力矩的主要原因。参考工况弹体过质心z向力矩变化主要出现在侵彻初期，见图11(b)。若靶内嵌埋硬质球形颗粒，典型时刻W-3 的弹靶相互作用见图13，除参考工况的所有诱偏因素外，颗粒强度差异引起的靶强度分布不均加剧了弹体结构变形，进一步改变弹体运动轨迹，体现在弹体与颗粒相互作用时弹体过质心z向力矩剧烈变化，见图11(b)。

图12 参考工况下不同时刻弹体变形及弹靶相对位置Fig. 12 Projectile deformation and relative location of projectile and target at different times in the reference case

综上所述，当嵌埋颗粒半径为弹体直径5 倍时，可达到折减弹体有效侵深的目的，但遮弹效果随颗粒埋深变化不单调，而颗粒强度越高，遮弹效果越显著。嵌埋颗粒遮弹机理主要体现为诱偏来袭弹，使其向着靶面偏转，而高强度硬质颗粒增加弹体侵彻阻力也是颗粒遮弹的原因之一，但弹体结构变形的内能耗散不是折减弹体有效侵深的主要机制。

2.3 硬质球形颗粒尺寸的影响

Wu 等[19]认为，在侵彻混凝土过程中，高强颗粒直径需在弹径1.5 倍以上，对弹体运动轨迹影响才会显著。为此，本文研究4 种颗粒半径，与弹径之比分别为1、2、5 和10，球心位于(200, 35, 0)，g1=2。弹体运动参数见表2，弹尖在xy平面内运动轨迹见图14。可见，颗粒半径为1 倍弹径时，弹体有效侵深不降反增，而颗粒半径在2 倍弹径以上时，弹体有效侵深有所降低。

弹体质心x向侵彻阻力及过质心z向力矩见图15。弹体质心x向位移随颗粒半径增大而减少，表现为弹体质心x向过载较参考工况的增加部分幅值及持续时间随颗粒尺寸增大而增加。当颗粒半径达10 倍弹径时，颗粒强度较混凝土强度的增加部分能有效折减弹体侵深。颗粒半径是弹径5 倍时，侵彻阻力增加及弹道偏转作用均较为突出。当颗粒半径较小时，如1 倍、2 倍弹径时，颗粒的主要作用是偏转弹道，但受颗粒作用位置、弹体姿态等影响，弹道若向有效侵深方向偏转，有效侵深可能增加，将不能达到遮弹效果。

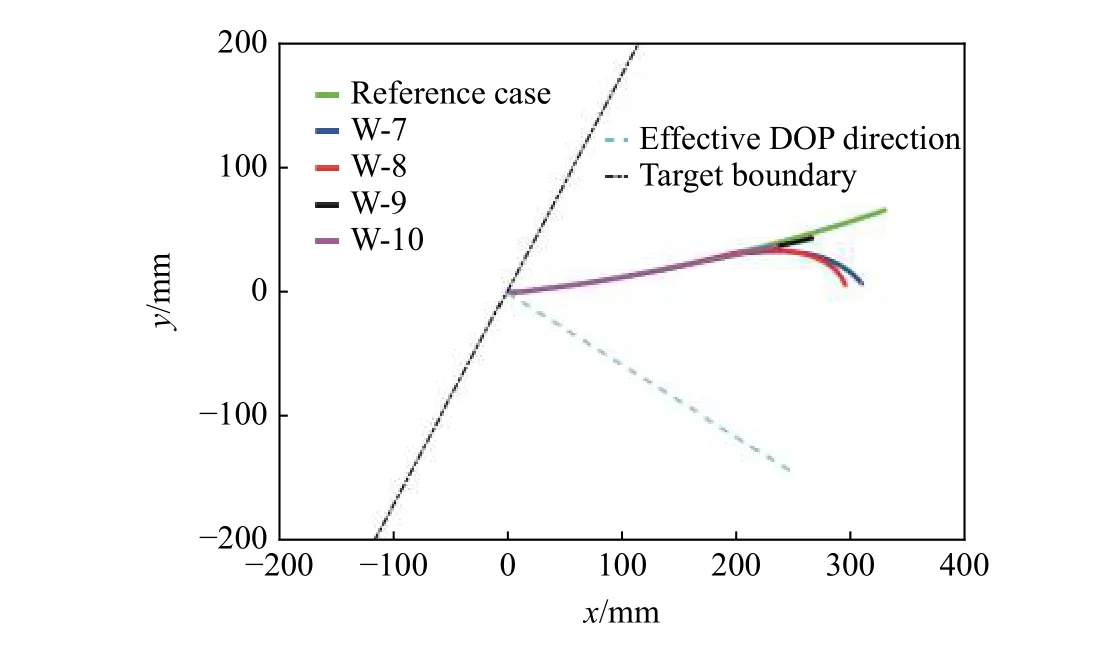
图14 颗粒尺寸变化时弹尖在xy 平面内的运动轨迹Fig. 14 Trajectory of nose tip in xy plane with variation of aggregate diameter

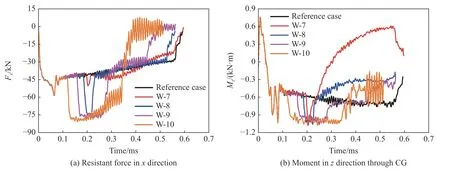
图15 颗粒尺寸变化时，弹体质心x 向阻力及过质心z 向力矩的时间历程（125 k Hz 低通滤波）Fig. 15 Time histories of x-directional resistant force and z-directional moment through projectile mass center for the projectile with variation of aggregate diameter (filtered by low pass filter with cutoff frequency 125 k Hz)

综上所述，颗粒半径从1 倍增大至10 倍弹径，颗粒对弹体的主要作用机理从以偏转弹道为主向偏转弹道与增加弹体侵彻阻力相耦合的方向发展。小颗粒尺寸时弹道偏转方向随机，可能对遮弹产生消极影响。颗粒半径在弹径5 倍以上时，侵彻阻力增加与弹道偏转的联合作用将有效折减弹体侵深。为此，为发挥良好的遮弹作用，建议遮弹颗粒半径应选择在5 倍弹径以上。

3 结论与讨论

基于动态空腔膨胀模型，计及有限大混凝土靶所有自由面衰减效应及颗粒强度改变，建立含球形颗粒有限大高强混凝土靶侵彻阻力表征模型。采用弹靶分离方法，数值模拟分析了颗粒位置、强度及尺寸对弹体运动及变形影响。结果表明：嵌埋颗粒半径为5 倍弹径时，可达一定的遮弹效果。此时，遮弹效果主要取决于弹体与颗粒作用的姿态，其随颗粒位置变化无明显规律。颗粒强度越高，遮弹效果越显著。颗粒半径从1 倍弹径增大至10 倍弹径，颗粒对弹体的作用机理以偏转弹道为主转变为偏转弹道与增加弹体侵彻阻力相耦合。综上所述，嵌埋颗粒遮弹机理主要体现在诱偏来袭弹，使其向着靶面偏转，而高强度颗粒增加弹体侵彻阻力从而降低弹体可达侵深也是遮弹机理之一，但弹体结构变形的内能耗散不是折减弹体有效侵深的主要机制。

颗粒半径在弹径的5 倍以上时，弹道偏转与侵彻阻力增加两种效应相耦合，单层密排颗粒组成的遮弹层即可达到相当的遮弹效果。然而，小颗粒半径（如1～2 倍弹径）时，颗粒对弹体作用机理主要表现为偏转弹道，与颗粒作用时弹体撞击位置与弹道偏转方向相关，存在随机性，可能增加弹体有效侵深而不利于遮弹。为发挥良好遮弹效果，采用小颗粒制作遮弹层时必须选择多层错排，遮弹层厚度应在10 倍弹径之上，一方面增加弹与颗粒作用距离，同时增加弹体向远离有效侵深方向偏转的概率。

本文中采用修正的球形动态空腔膨胀模型表征弹体侵入含球形颗粒混凝土靶的表面压力，而空腔膨胀理论假设侵入介质均匀各向同性。当靶材不满足该假设时，理论适用性需进一步研究分析。然而，所谓球形颗粒，可看作广义的混凝土骨料。即使混凝土主要由骨料与砂浆两相组成，为典型非均质材料，但球形空腔膨胀理论的分析结果与大量的混凝土侵彻试验结果吻合良好[20]。这说明球形空腔膨胀理论不仅可适用于混凝土，也可拓展使用于含球形颗粒的混凝土侵彻阻力表征。本文的侵彻阻力模型选择具有合理性。

实际侵彻过程中，弹体可能磨蚀、弯折破坏甚至破碎，将降低其侵彻性能。本文中未考虑弹体破坏影响，是对结构防护性能的保守分析，结果可用于遮弹层防护结构设计。