冲击速度和轴向静载对红砂岩破碎及能耗的影响*
2020-10-23金解放王熙博钟依禄
金解放,吴 越,张 睿,王熙博,余 雄,钟依禄
(1. 江西理工大学建筑与测绘工程学院,江西 赣州 341000;2. 江西理工大学资源与环境工程学院,江西 赣州 341000)
利用钻爆法进行地下工程岩体开挖时,工程岩体承受的是静载荷和动载荷的组合载荷[1]。爆破破岩有两个关注重点:一是岩石破碎的能量耗散问题,它是优化破岩效率、提高生产力的关键,也是岩石破碎理论的基础[2];二是岩石破碎的块度分布,是岩石破碎程度的直观表现,表征岩石破碎程度的标准度量[3]。承受的载荷形式对岩石破坏模式和破碎块度分布有较大影响[4]。研究爆破冲击载荷下岩石破碎模式及破碎机理,有助于高效破岩及节省能耗,提高矿山企业的经济效益。
众多学者就爆破冲击载荷作用下岩石破碎分布、能量耗散及岩石破碎机理展开了研究。金解放等[5]对砂岩进行三维循环冲击实验,研究了三维静应力下砂岩的动态疲劳破坏模式和机理。Li 等[6]研究了中等应变率下花岗岩的破碎特性,花岗岩能量耗散与应变率具有线性关系。赵光明等[7]利用数值模拟方法研究了类岩材料的破坏模式和能耗特性,结果表明,岩石的破坏模式有张应变、轴向劈裂拉伸和压碎等3 种,且破坏模式和能耗都具有应变率效应。黎立云等[8]对砂岩试件进行不同冲击速度下的破坏试验,研究了冲击速度对试件破坏能量耗散特性的影响。许金余等[9]等研究了大理岩破碎程度与分形维数之间的关系,得到大理岩分形维数与比能量吸收值之间具有线性关系。江红祥等[10]研究了冲击速度对煤岩破碎能量、粒度分布的影响。Yin 等[11]在动静组合加载试验装置的基础上,增加了气压装置,研究了瓦斯气压和轴压对煤岩冲击破碎程度和能量耗散的影响,得到了一些有益的结果。Li 等[12]研究了花岗岩在40~150 s−1应变速率下的动态破碎特性,得到了花岗岩由Ⅰ类到Ⅱ类转化时的破坏模式,并建立了考虑多维破碎的碎片模型。上述研究极大地丰富了岩石冲击动力学的研究理论,但研究岩石的破坏模式、破碎程度和能量耗散时多以应变率进行表征,属于岩石动力学的率相关性研究,且应变率的变化范围相对较窄。工程实际中,多数工况下可以测得或控制爆破动载荷的大小,且爆破应力波大小的变化范围非常大,研究不同大小冲击载荷作用下岩石的能量耗散和破坏特性更有利于工程实际应用。
地下工程岩体在爆破开挖时,由于爆破应力波的衰减效应,距爆破震源不同距离处承受的冲击动载荷大小不同;距爆破震源越远的地方,爆破应力波幅值和应力波携带的能量越小[13-14]。由于开挖卸荷,地下巷(隧)道围岩体中不同空间位置处的地应力大小不同,距隧道壁径向越远的位置,其径向应力越大,环向应力越小[15]。已有研究表明[16-17],岩石是否承受静载荷以及承受静载荷的大小对岩石动态力学响应有重要的影响。因此在研究爆破动载荷对不同空间位置处围岩体的破坏模式及机理、能量耗散和破碎程度时,应系统考虑冲击载荷和静应力大小的影响。
本文中,利用动静组合加载试验系统,通过改变冲头撞击速度,模拟工程中不同空间位置处应力波幅值的大小或携带的能量;通过调整轴向静应力的大小,模拟工程岩体中径向地应力的变化情况;选用红砂岩制备试件,轴向静应力分别设置为单轴抗压强度的0%、15%、30%、45%、60%、75%、90%等7 种工况,分别用4.0、6.0、8.0、10.0、12.0、13.5 和15.0 m/s 的撞击速度进行冲击试验;研究冲击载荷和轴向静应力大小对岩石破坏模式、破坏机理、能量耗散和破碎程度的影响,以期为更合理地开采和破碎矿石提供理论依据。
1 试 验
1.1 试验装置
采用江西理工大学冲击实验室的动静组合加载试验装置,如图1 所示。该试验装置的入射杆、透射杆和缓冲杆的直径都为50 mm,长度分别为2 000、1 500、500 mm。轴压加载装置通过手动液压泵提供动力,压力大小由手动液压泵的液压表显示,其最小刻度为0.5 MPa。利用粘贴在入射杆、透射杆上的应变片、CS-1D 超动态应变仪和DL-750 示波器,分别采集冲击过程中的入射波、反射波和透射波。
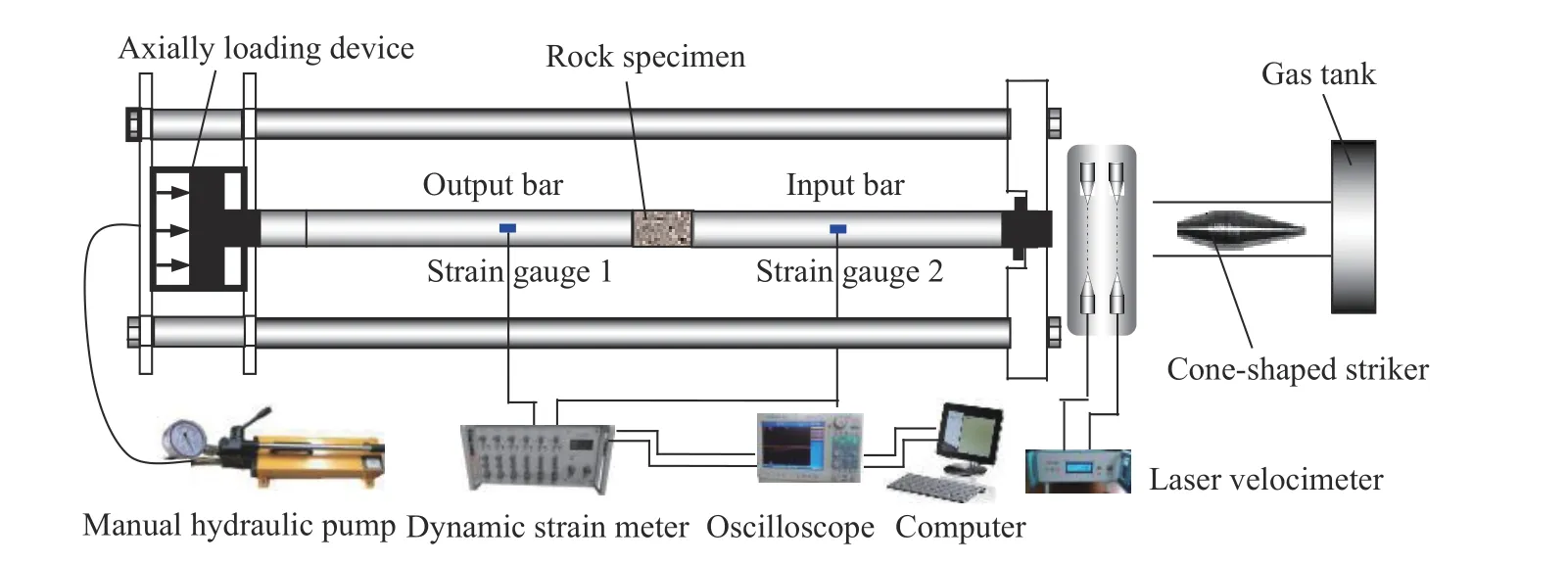
图1 动静组合加载试验装置Fig. 1 Experimental setup with static-dynamic coupling loading
使用纺锤形冲头实现近似半正弦波加载,最大程度消除PC 振荡,冲头质量为1 970.38 g,尺寸如图2(a)所示。当轴向静应力为零,即σs=0,冲头冲击速度v=8.15 m/s 时的入射波如图2(b)所示。由图2(b)可以发现,当无轴向静应力时,本研究所使用的冲头撞击产生的入射波延时约173 µs。

图2 异形冲头尺寸及入射波波形Fig. 2 Cone-shaped striker dimensions and incident wave
1.2 试 件
试件选用密实均匀和完整性良好的红砂岩制备,试件尺寸为 ∅ 50 mm×50 mm,按照岩石力学的试验测试要求,对试样端面进行仔细打磨,试样两个端面的不平整度小于0.02 mm,端面法线偏差小于0.25°。试件的平均密度为2.46 g/cm3,平均单轴抗压强度为60 MPa,平均纵波波速为2 091 m/s。单轴压缩应力应变曲线如图3 所示,当试件承受不同的轴向静应力时,试件具有不同的压实密度或损伤状态,进而具有不同的物理力学参数。
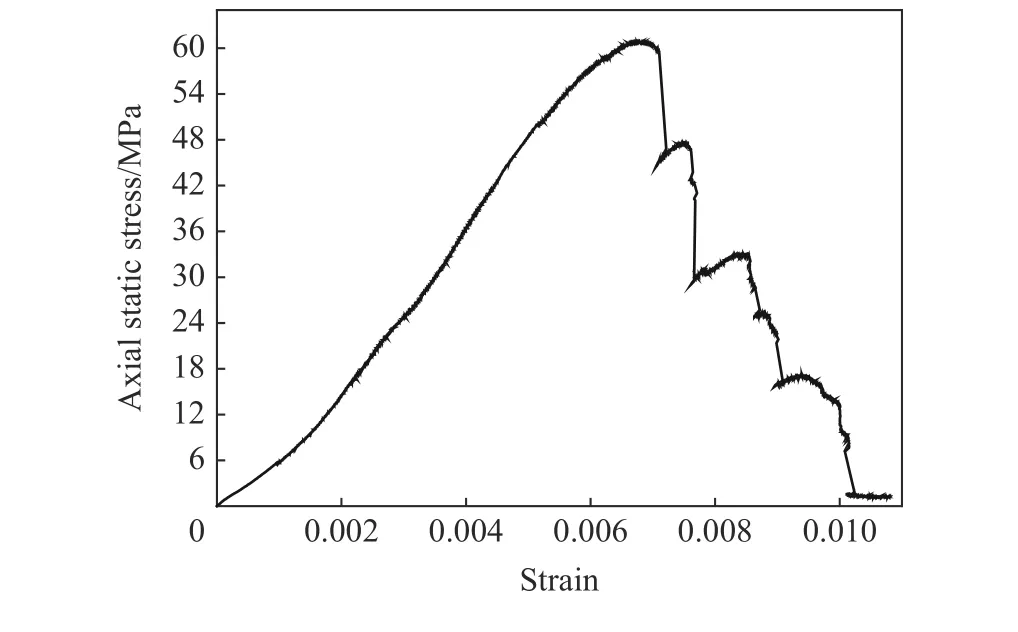
图3 单轴压缩应力-应变曲线Fig. 3 Stress-strain curve of red sandstone under uniaxial compression
1.3 试验方案
冲击载荷的大小用冲头的冲击速度衡量。冲击速度和轴向静应力(轴压)的设置如表1 所示,表中轴向静应力是根据岩石试件的单轴抗压强度选定的,分别对应单轴抗压强度的0%、15%、30%、45%、60%、75%、90%。根据冲头质量和冲击速度,可以计算出冲击动能。

表1 静载荷和冲击速度设置Table 1 Setting of static load and impact velocity
1.4 能量耗散计算
根据试验所得的入射波εi(t)、反射波εr(t)和透射波εt(t),结合一维应力波理论和冲击动力学,可以分别计算出入射能、反射能和透射能:
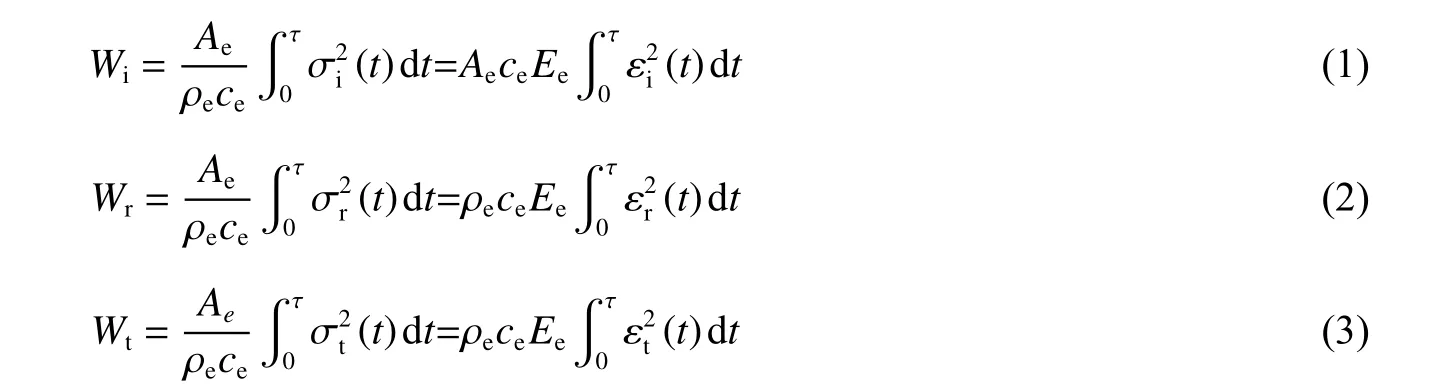
式中:Wi、Wr、Wt分别为入射能、反射能、透射能,Ae、ρe和ce分别为弹性杆的横截面面积、密度和纵波波速,τ 为应变波的延续时间。
根据能量守恒原理,忽略试件破坏时碎片的弹射动能和试件与弹性杆之间摩擦消耗的能量,认为入射能与反射能和透射能的差值全部是试件消耗的能量,即在冲击试验过程中试件消耗的能量Wa为:

2 冲击速度对破坏模式及机理的影响
严格按照设定好的试验方案进行冲击试验,采集记录入射波、反射波和透射波,并收集冲击后的岩石试件,结果如表2 所示,表中D为破碎分形维数。
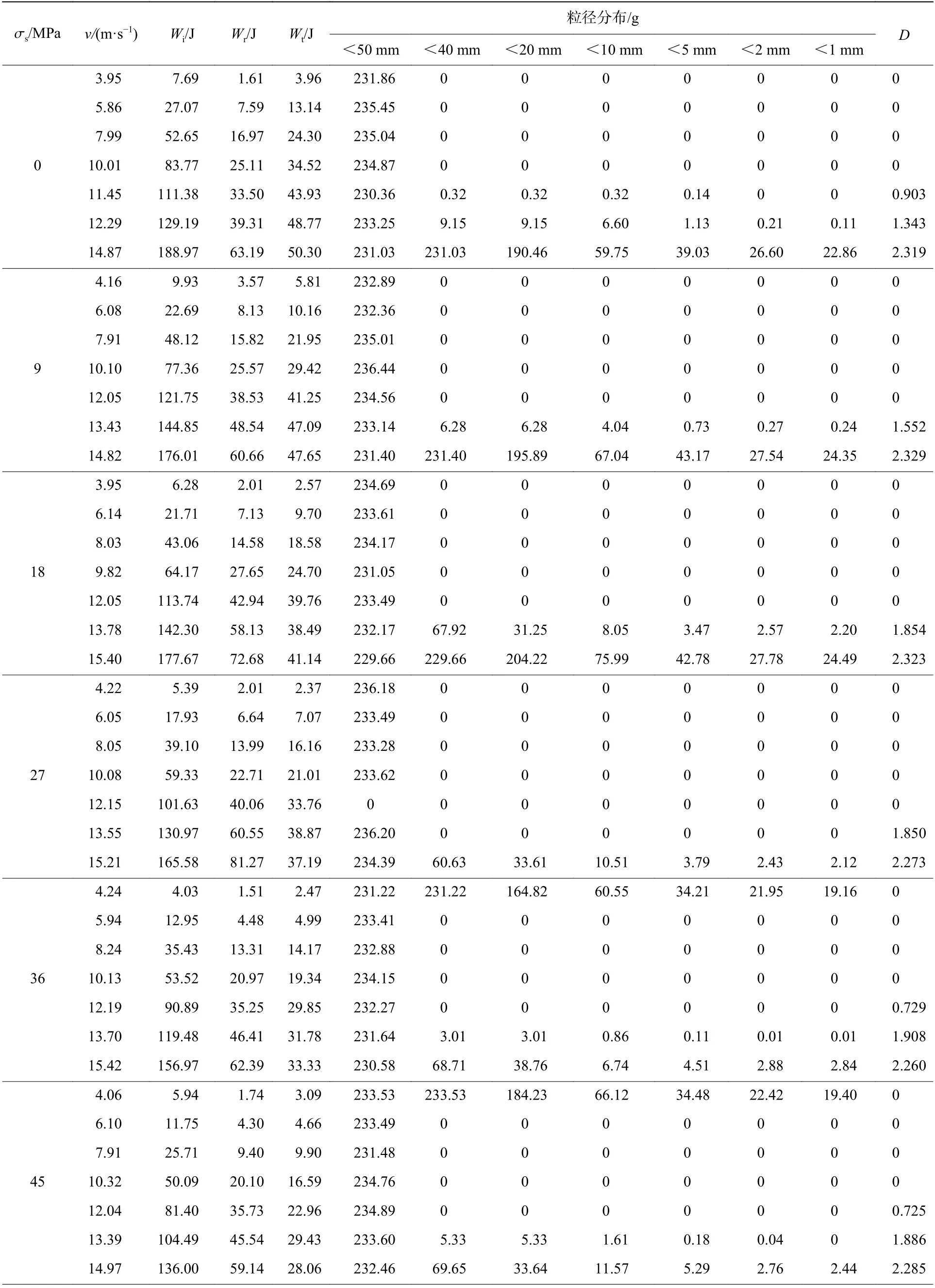
表2 冲击试验工况及试验结果Table 2 Conditions and results of impact experiments
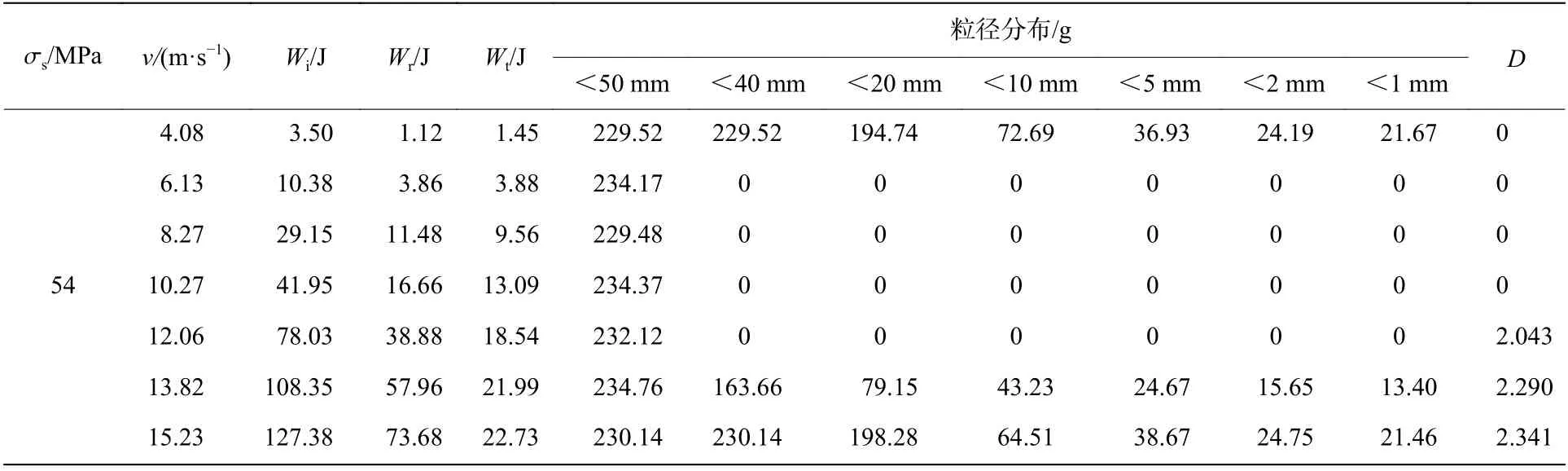
续表2
2.1 无轴压时岩石的破坏模式
图4 为无轴向静应力时岩石试件受到冲击后的结果。由图4 可以看出,当冲击速度较低时,岩石试件没有发生宏观破坏。随着冲击速度的升高,岩石试件的破坏程度依次是整体完整、局部破坏、整体破坏、粉碎性破坏。当冲击速度不高于10.01 m/s,承受冲击载荷作用后,岩石试件完整无宏观失效。当冲击速度为11.45 m/s 时,岩石试件与入射杆的接触端面,有碎片脱落,发生局部小范围的破坏。本文中定义岩石试件不发生宏观破坏所承受的最高冲击速度为临界冲击速度,根据图4 可以预测无轴向静应力时,红砂岩的临界冲击速度应高于10.01 m/s、低于11.45 m/s。当冲击速度高于临界冲击速度时,破坏后岩石试件的碎片数量随冲击速度的升高而增大,小粒径块度的占比增大,表明岩石试件破碎程度加剧。综上所述,冲击载荷大小对岩石的破坏结果有重大影响,存在岩石由不破坏到破坏的临界冲击速度。

图4 不同冲击速度作用后的岩石试件Fig. 4 Rock specimens subjected to under different impact velocities
从图4 可以发现,当岩石试件发生宏观破坏时,靠近入射杆端面(前端)的破碎程度大于另一端(后端)的破坏程度。这表明,动载应力波在岩石试件中传播时,试样前端的破碎和裂纹扩展消耗了更多的应力波能量,而后端消耗的应力波能量相对较少。
由图4(d)~(f)可以看出,岩石试件破坏后的主体破裂面都近似与试件轴向平行,没有出现端面效应现象,破裂面无摩擦痕迹,破坏后的主体仍近似为圆柱体。分析认为,无轴向静应力工况下岩石试件破坏后的主破裂面几乎与轴线平行,这是由于利用动静组合加载试验装置进行冲击试验时,当弹性杆与试件之间无压力作用时,且由于弹性杆和岩石试件之间涂抹黄油等润滑剂,弹性杆与岩石端面之间的摩擦力非常小,几乎为零[18],即岩石在冲击过程中的端部效应几乎为零。在动态压缩应变的同时,岩石试件在长度方向的横向拉伸应变相同,试件的破裂面与轴线近似平行。
根据上述试验结果,对无轴压作用的红砂岩试件,不同冲击速度下的破坏模式如图5(a)所示,其中轮廓线1 表示冲击速度较低时,试件无宏观破坏;轮廓线2 和3 表示冲击速度高于临界冲击速度时,沿试件轴线方向的整体破坏,两者的区别是轮廓线3 的破坏程度比轮廓线2 的更严重,入射端面积较透射端的小。
2.2 无轴压时岩石的破坏机理
由图4 和图5(a)可以看出,对无轴向静应力红砂岩试件,冲击载荷使试件发生快速轴向压缩变形,由于泊松效应,试件同时发生横向扩张变形。由于试件端部摩擦力几乎为零,试件沿轴线方向的横向扩张变形程度几乎相同。当冲击载荷过大,横向最大伸长线应变达到红砂岩的极限伸长线应变时,圆柱体外层区域(图5(a)中虚线和实线中间区域)优先与中间主体脱落,该圆环体在发生横向扩张变形时,由于体积的增大,圆环体内部同时发生环向拉伸变形,出现不同数量的裂纹,圆环体破碎成若干数量的弧形片状体。随着冲击速度的继续升高,岩石试件入射端外层区域剥离的厚度加大,剥离下来的弧形岩块被冲击成尺寸更小的碎片、岩粒或碎屑。因此,无轴压红砂岩在不同冲击速度作用下的破坏属于张拉破坏,是由于岩石的最大拉应变达到极限值的破坏。
2.3 有轴压时岩石的破坏模式
图6 为轴向静应力等于27 MPa、不同冲击速度作用后的岩石试件。由图6 可以看出,冲击速度对岩石的破碎程度有较大的影响,随冲击速度的升高,岩石试件的破坏程度依次是整体完整、整体破坏、粉碎性破坏,这与无轴向静应力时的结果类似。就文中设置的冲击速度范围而言,当冲击速度低于13.55 m/s 时,岩石试件没有发生宏观破坏;冲击速度为13.55 m/s 时,试件发生宏观破坏,但仍有一主体存在,可以继续承受载荷作用;当冲击速度为15.21 m/s 时,岩石发生粉碎破坏,没有试件主体存在。
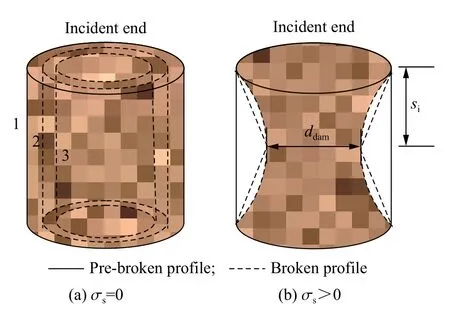
图5 不同冲击速度作用下红砂岩破坏模式Fig. 5 Failure modes of red sandstone under different impact velocities

图6 轴向静压为27 MPa 时不同冲击速度动载荷作用后的岩石试件Fig. 6 Rock specimens subjected to axial static stress of 27 MPa and dynamic loading of different impact velocities
为了分析不同轴向静应力时岩石的破坏模式和机理,选择冲击试验后发生宏观破坏且有明显主体存在的试件。经过对比破坏后的岩石试件,选择冲击速度近似为13.5 m/s 的试验试件,如图7 所示。由图7 可以看出,当岩石试件具有轴向静应力时,在近似相同冲击速度的动载荷作用下,试件的破坏形态和程度不同。当轴压较小时(9 MPa),试件仅在入射端发生破坏,具有明显的端部效应;随着轴向静应力的升高,小粒径的碎片占比增大,当轴压处于18~45 MPa 之间时,试件宏观破坏后仍有一个主体,可以继续承受载荷作用;当轴压为54 MPa 时,冲击破坏后试件已全部破碎,不能继续承受外载荷。

图7 冲击速度约为13.5 m/s、不同轴压下岩石的破坏模式Fig. 7 Failure modes of rock under impact velocities of about 13.5 m/s and different axial static stresses
从图7 还可以看出,当试件具有轴向静应力时,试件的破坏都具有明显的端部效应。这是由于静载荷增大了试件与弹性杆之间的端部效应。当轴向静应力适中时(σs≤45 MPa,即单轴抗压强度的75%),冲击破坏后岩石试件仍有一个主体,该主体能继续承受载荷,其形状为沙漏状或X 状共轭体,破坏面具有明显的摩擦痕迹,摩擦面参差不齐,这与工程实际中矿柱的破坏模式吻合,如图8 所示[19]。随着轴压的升高,岩石碎块由(弧形)片状体转变成碎块。上述分析表明,工程实际围岩体承受相同大小的动载荷时,具有的地应力大小对其破坏模式和破坏结果有重大影响,存在一个适中的轴向地应力值(或单轴抗压百分比),当实际地应力小于该值时,破坏后的岩体仍有一个主体,能继续承受地应力,当实际地应力值大于该适中值时,破坏的岩体丧失承载能力。
根据图7,可以归纳出具有轴向静应力的红砂岩试件在不同冲击速度下的破坏模式,如图5(b)所示。不同轴压工况下,岩石破碎的结果可以用图5(b)中的si和ddam衡量,其中si为最小横截面距入射端的距离,ddam为岩石试件破坏后最小横截面直径。若岩石发生整体宏观破坏,si和ddam越小,表示试件破坏面积越大,试件破坏越严重。图5(b)中的si和ddam如表3 所示,其中轴压为54 MPa 时试件已完全破碎,破坏后已无试件主体,仅有位于透射端的一个圆锥体,其高度为15.90 mm,此时认为ddam的破裂位置处于破坏长度(试件的长度减去透射端圆锥体的高度)的中间位置。
根据表3,红砂岩试件破坏后的si和ddam随轴压的变化关系,如图9 所示。根据图9 可得,随着轴压的升高,si先增大后减小,ddam呈现减小-缓慢减小-快速减小的趋势。

图8 艾略特湖矿破碎矿柱[19]Fig. 8 A crushed mine pillar at the Elliot Lake mine[19]

表3 冲击速度约为13.5 m/s 时试件破坏的si 和ddam 值Table 3 Values of si and ddam in main part of destroyed specimens at the impact velocity of around 13.5 m/s

图9 试件破坏的si 和ddam 值与轴压的关系(v≈13.5 m/s)Fig. 9 Changes of si and ddam with axial static stress for a broken specimen when the impact velocity equals to 13.5 m/s approximately
2.4 有轴压时岩石的破坏机理
对于有轴压的红砂岩试件,受冲击载荷作用时,由于轴向压缩变形,试件必然发生横向扩张变形。由于轴向静应力的存在,试件与弹性杆接触端具有阻止试件发生横向变形的摩擦力,即出现沿轴线方向的不均匀横向变形,试件两端附近区域的横向变形被限制,而中间部位的横向变形被束缚的程度较小。当轴向压缩变形较大时,横向扩张的线应变超过极限线应变时,试件会出现如图5(b)所示的共轭破裂面,拉伸应变能力不足是发生破坏的一个主要因素。
图10 为岩石试件的受力示意图,其中σs为轴向静应力,σd为冲击动应力,σf为试件的横向约束力,σresu为合应力,θ 为合应力与试件端面的夹角。当合应力σresu达到岩石的抗剪强度时,试件将发生剪切破坏,岩石的破坏是由抵抗拉伸和剪切能力不足引起的。在均匀性和各项同性假设的前提下,平行轴线方向不同点处的横向约束力大小不同,试件两端的约束力较中间部位大。由于试件的长径比较小,可以认为平行轴线方向不同点处的σs+σd大小相同。由图10 可知,岩石破裂面与端面的夹角θ 两端小中间大,理论上岩石试件破裂面应是图5(b)中所示的弧线形状,这也能被试验结果验证,如图7(b)主体的右侧和图7(d)中的左侧都是弧线图。但多数结果如图5(b)中的折线形状,这主要有两个原因:一是岩石是脆性材料,在冲击载荷作用下,破裂面在极短的时间内完成(100 µs 左右)[20-21],试件在破碎过程中,图5(b)中平面破裂面面积小于弧形破裂面面积,在破裂过程中平面破裂面消耗的能量少,因此易出现X 共轭形状破裂;二是试件的长径比小,由于端部效应,试件中横向约束力为零或接近为零的区段不明显,导致图5(b)中切线竖直或接近竖直的弧线段缺失。
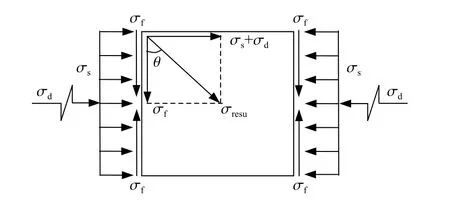
图10 冲击载荷作用下具有轴压试件的受力示意图Fig. 10 Free-body diagram of a specimen under coupled axial static stress and impact loading
3 能量耗散的变化规律
基于式(1)~(3),根据冲击试验所得的入射波、反射波和透射波数据,不同冲击速度下入射能、反射能、透射能如表2 所示,进而根据式(4)可以计算出冲击过程中试件的耗散能。图11 给出了轴压为0、18、36 和54 MPa 时入射能、反射能、透射能和耗散能随冲击速度的变化关系。
图11(a)中的冲头冲击动能为冲头撞击入射杆时携带的能量,由冲头质量和冲击速度根据动能的计算方法得到,因此冲头冲击动能与冲击速度之间是二次函数关系。由图11(a)可以看出,入射能随着冲击速度的升高而升高,两者具有良好的二次函数关系。入射能与冲击速度之间的二次函数关系有两个原因:一是冲击动能与冲击速度就是二次函数关系,二是由式(1)可以看出,入射能与入射应力波幅值也呈二次函数关系。轴向静应力对入射能随冲击速度的变化路径影响较大,相同冲击速度下,轴向静应力越大,入射波能量越低,都低于冲头的冲击动能。分析认为,由于冲击试验时采用异形冲头(如图2(a)所示),其撞击端的横截面直径为18.44 mm,小于入射杆的直径(50 mm),根据一维应力波理论,冲头的广义波阻抗(ρcA,其中ρ 为密度,c为纵波波速,A为横截面面积)小于入射杆的广义波阻抗,冲头的冲击能量不能完全进入弹性杆;当入射杆具有轴向静应力时,相同冲击速度下,弹性杆中入射波的幅值随轴向静应力的升高而线性减小[22],这也必然导致其入射能随轴向静应力的升高而降低。上述这些入射能的变化规律仅是弹性杆的特性,与岩石试件无关。

图11 不同轴压下能量随冲击速度的变化Fig. 11 Energy varied with impact velocity under different axial static loads
由图11(b)可以看出,随着冲击速度的升高,反射能逐渐增加,与冲击速度呈二次函数关系,且切线斜率越来越大。轴压的大小对反射能与冲击速度的演化路径有影响。
由图11(c)可以看出,透射能随着冲击速度的升高而升高,但升高幅度越来越小。相同冲击速度下,透射能随着轴压的升高而降低。对比图11(b)和(c)可以发现,轴向静应力对透射能的影响较对反射能的影响大。
由图11(d)可以发现,在入射能、反射能和透射能随冲击速度变化的基础上,红砂岩耗散能随冲击速度的升高而增加,两者之间满足二次函数关系。根据SHPB(split Hopkinson pressure bar)的能量分析理论,认为耗散能与试件的损伤及破坏息息相关,在冲击载荷作用下,试件的耗散能越大意味着岩石的损伤程度或破碎程度越高。这表明,对具有不同轴向静应力的岩石试件,尽管较低的冲击速度不能使试件发生宏观破坏(如图4(a)~(c)以及图6(a)~(b)所示),但仍会对试件造成不同程度的损伤,冲击速度越高,损伤程度越高,直至试件发生宏观破坏。
由图11(d)还可以发现,岩石试件承受的轴向静应力对冲击速度和耗散能之间的演化路径有较大的影响,随着轴向静应力的升高,耗散能的增加幅度越来越小,且随冲击速度的升高,减小的趋势越来越明显。这表明,轴向静应力不仅对岩石破碎时的能量耗散有影响,对没有发生宏观破坏的岩石内部损伤也有影响。
4 冲击试验的碎块分形
本节从岩石破碎粒径大小及分布的角度研究冲击速度对岩石动态力学特性的影响。
4.1 破碎块度的分布
对冲击后发生宏观破坏的岩石试件,采用孔径为0.5、1、2、5、10、20、40 和50 mm 的标准筛进行筛分,将岩石试件破碎块度分为0~0.5、>0.5~1、>1~2、>2~5、>5~10、>10~20、>20~40、>40~50 mm 等10 个等级,不同工况下岩石试样的破碎块度分布结果如表2 所示。
由表2 可以发现,不同冲击速度下岩石破碎后的块度分布不同。相同轴压工况下,随着冲击速度的升高,小粒径碎块的质量增大,大粒径碎块的质量相应减小。为了更好地量化岩石破碎块度分布与冲击速度的关系,后文通过破碎块度分形维数进行分析。
4.2 破碎分形维数的确定
分形理论在岩石力学众多研究领域得到广泛的应用[23-25]。研究表明,岩石在冲击破碎后其块度分布与粒径之间也具有较好的分形特性[9,26]。根据质量-频率关系[27],岩石试件冲击破碎粒径的分布方程为:

式中:x为碎块粒径,xm为破碎岩块的最大尺寸,D为块度分布分形维数,M(x)为尺寸小于x的碎块累计质量,Mtot为碎块总质量。
对式(5)两边取自然对数得:
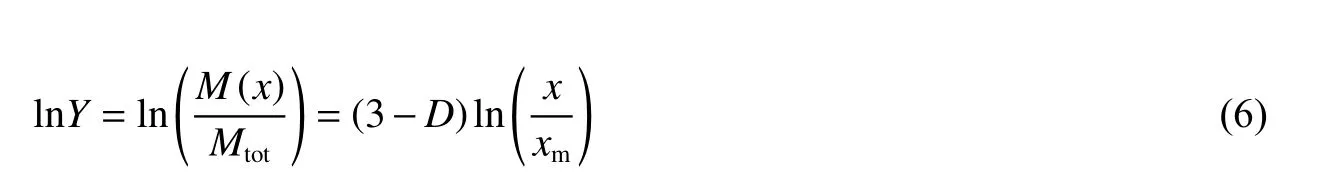
对表2 中不同工况下岩石破碎的筛分结果,根据式(6)可以在ln(M(x)/Mtot)-ln(x/xm)坐标中画出块度质量与粒径分布之间的关系,如图12 所示,其拟合直线的斜率为(3-D),进而可以确定岩石试件破碎的分形维数D。
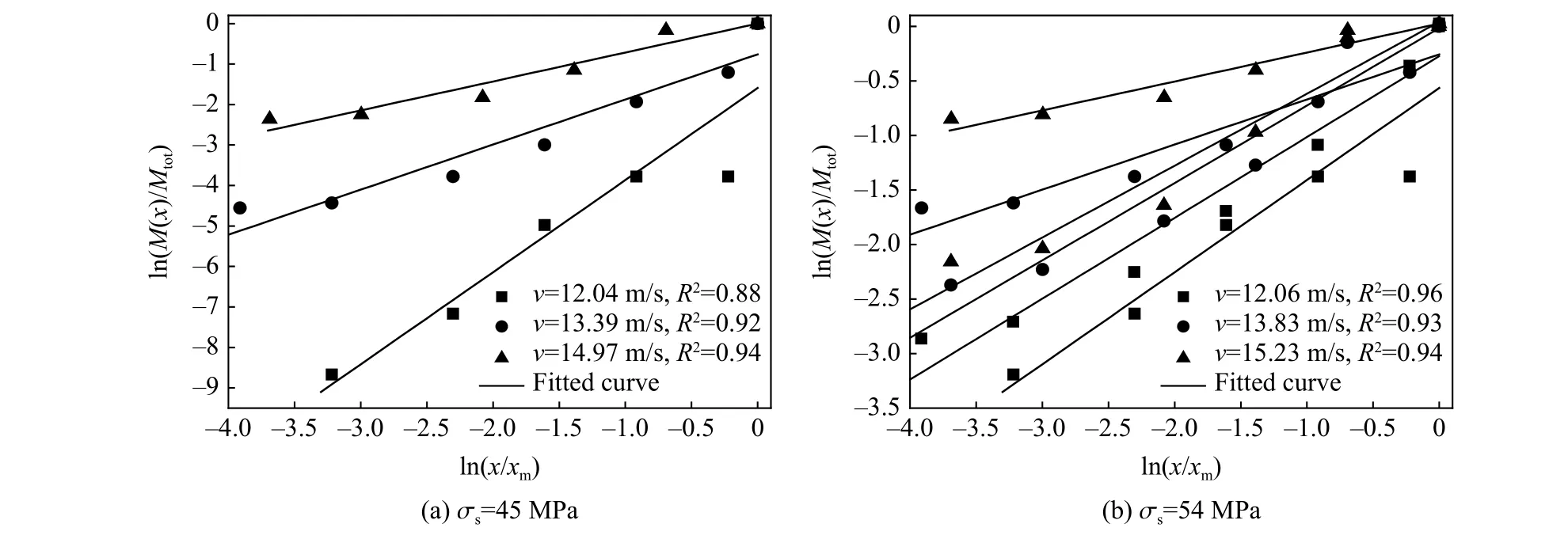
图12 轴压为45 和54 MPa 时破碎试件的ln(M(x)/Mtot)-ln(x/xm)关系Fig. 12 ln(M(x)/Mtot)-ln(x/xm) relations for broken specimens with the axial static stresses of 45 and 54 MPa, respectively
由图12 可以看出,破碎块度质量与粒径分布之间的线性相关性高,表明在不同冲击速度下,具有轴向静应力红砂岩试件的破碎具有良好的自相似性,可以用分形维数定量地表征岩石试件的破碎程度。不同工况下岩石的破碎分形维数如表2 所示,需要说明的是,为了统一分析不同冲击速度对破坏结果的影响,对承受冲击载荷后没有发生宏观破坏的岩石试件,本文中暂且令其分形维数等于零。
4.3 分形维数与冲击速度的关系
由表2 中不同冲击速度下岩石的分形维数,可以画出不同轴向静应力下岩石分形维数随冲击速度的变化关系,如图13 所示。由图13 可以发现,随着冲击速度的升高,岩石分形维数由零逐渐增加,在设置的冲击速度范围内,最大分形维数都在2.3 左右。当试件具有不同轴向静应力时,随着冲击速度的升高,图13 中分形维数由零转为大于零对应的冲击速度(即临界冲击速度vcr)不同。随着轴向静应力的升高,临界冲击速度先升高后降低,其变化趋势如图14 所示。当轴压为0 和54 MPa 时,当冲击速度超过临界冲击速度时,分形维数随冲击速度的演化趋势较平缓,而轴压为9、18 和27 MPa 时,演化趋势较陡峭,即:轴向静应力为零或接近单轴抗压强度时,分形维数随冲击速度的演化趋势较平缓;轴向静应力处于岩石弹性阶段时,分形维数随冲击速度的演化趋势较陡峭。
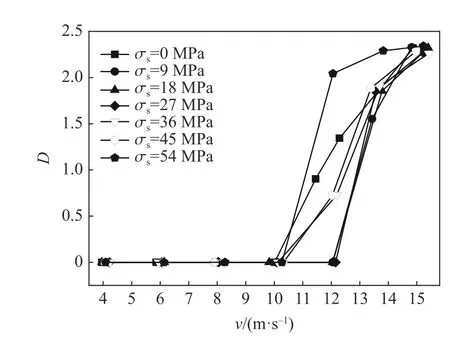
图13 冲击速度与分形维数的关系Fig. 13 Fractal dimension varied with impact velocity

图14 岩石临界冲击速度与轴向静应力的关系Fig. 14 Critical impact velocity of rock varied with axial static stress
5 结 论
针对地下岩体工程爆破开挖,距爆源不同距离处的地应力和冲击载荷大小都不同的工程实际,利用动静组合加载试验装置,对红砂岩进行不同轴向静应力和冲击速度冲击试验,研究冲击速度和轴向静应力对岩石破坏模式和机理、破碎分形维数以及能量耗散的影响,主要结论如下:
(1)随着冲击速度的升高,岩石的破坏程度依次是整体完整、局部破坏、整体破坏、粉碎性破坏。随着轴向静应力的升高,临界冲击速度先升高后降低。这是由于随着轴向静应力的升高,岩石依次进入压密阶段和损伤阶段,具有不同的波阻抗;进入压密阶段时岩石的抗冲击能力最强,随着损伤程度的增大,岩石抗冲击能力降低。
(2)随着冲击速度的升高,无轴向静应力岩石宏观破裂面平行于试件轴线方向,破坏的原因是由于岩石伸长线应变能力不足,属于张拉破坏;有轴向静应力的试件破坏后的主体呈沙漏状或X 状共轭体,属于拉剪破坏。
(3)随着冲击速度的升高,入射能、反射能、透射能和耗散能都呈二次函数趋势增加,入射能、反射能和耗散能随冲击速度的变化曲线斜率越来越大,而透射能曲线斜率越来越小。轴向静应力对冲击速度与耗散能之间的关系有较大的影响,轴向静应力越高,耗散能的增加幅度越小,且随冲击速度的升高,减小的趋势越来越明显。
(4)红砂岩破碎块度与冲击速度之间具有正相关性,随着冲击速度的升高,岩石分形维数由零逐渐增大。轴向静应力为零或接近单轴抗压强度时,分形维数随冲击速度的演化趋势相对较平缓;轴向静应力使岩石处于弹性阶段时,分形维数随冲击速度的演化趋势越陡峭。
与用应变率表征岩石动态破坏结果相比,本文中建立的动载荷(用冲击速度量化)与岩石破坏和能耗特性关系更具有工程实际意义。
