基于MATLAB软件的运输路径优化研究

夏 强，周健勇 （上海理工大学 管理学院，上海200093）

0 引言

随着当今经济科技的快速发展，市场各行业竞争愈加激烈，物流也发展成为最具竞争性的行业之一。物流系统包含了采购、运输、存储、搬运、流通加工、信息处理等多个要素，但无论是其中哪一个功能单元，它的优化都是追求节约、高效的最优方案。在解决这个问题的过程中，通常会利用数学知识建立数学模型，力求找到最优解，从而获得最好的进行资源配置的有效方案。

目前物流工程最重要且急需解决的问题就是如何使物流活动适应现代化生产生活的需求，实现系统化、效率化，以及如何制定、选择什么样的物流方案才能获得最佳的经济效益[1]。众所周知，运输作为物流活动的核心，运输路径的选择是关系物流成本的首要因素，一个合理的运输路径对企业来说是必须掌握的。但运输路径往往涉及多个因素参与其中，比如单位运费、路径长短等都有不同程度的影响。因此运输路径的优化与选择是厂家重点解决的难题。如果单纯地依靠人工计算来寻找最优路径比较困难，运算过程复杂繁琐，不易简化。

1 商品运输路径问题研究

1.1 商品运输路径研究的基本观点。运输路径问题是由Dantzig和Ramseryu在1959年首次提出，涉及到物流、系统、管理等多个学科的理论知识，自提出以来，国内外许多研究者对这项问题进行了比较细致的探讨与研究，尽管各有不同的观点，但总体上的研究结果都表示运输路径对企业影响最大的无非是成本的消耗以及时间的长短从而影响到顾客满意度问题。商家在选择运输方案时，通常会考虑本企业运输成本、运输时间、运输距离等方面进行多角度的衡量，而成本是首要因素。对于本文中列举的水果罐头并非冷链运输，并不存在要考虑到运输时间导致的影响顾客满意度问题，考虑的首要因素同样是成本，以成本最小为每次运输的目标[2]。

1.2 商品运输路径优化的意义。为了提高物流运输的效率，节约运输成本，本文以某水果罐头加工厂为例，对运输路径优化后结果显示可大大降低运输中的成本，提高企业的收益。

（1）节约运输能力，节约能源支出；（2）能够降低企业运输的成本，减少不必要的支出;（3）减少因路径不合理而导致的资源浪费以及污染物的排放。

2 软件及函数简介

2.1 MATLAB概述。MATLAB是矩阵实验室（Matrix Laboratory）的简称，是一种用于算法开发，数据可视化、数据分析及数值计算的高级技术计算语言和交互环境[3]。MATLAB应用范围非常广泛，可以用来处理信号和图像、测试测量、开发程序、数学建模与分析，同时包含Simulink仿真程序，用来在各个学科的实验中进行仿真研究。

2.2 MATLAB的特点。MATLAB通过运算矩阵的方式计算数据，它把数值计算和可视化环境结合起来，具有简捷、易操作的特点[4]，应用领域非常广泛，同样在运筹学线性规划中发挥重要的作用。

在MATLAB中绘图十分方便，数据的可视化非常简单，并且绘制的图形层次分明，尤其在绘制3D图形中，优势极为明显，其强大的绘图功能也是在处理数学模型问题中不可缺少的工具。

MATLAB软件中具有功能丰富的工具箱，由各专业领域的专家编写应用于本领域的工具，使用户无需自己编写便可直接使用，本文中使用的linprog函数便是出自其中。

2.3 线性规划简介。线性规划是运筹学中的一个重要分支，它是处理线性目标函数和线性约束的比较成熟的方法。建立线性规划模型在影响因素较多环境下可将问题明确化，使研究问题更加直观，在经济、军事、商业、运输以及教育系统中都有广泛的应用。依靠数学软件的强大运算能力，能简化模型的求解，运用相应的方法便能求解到最优的运输路径，运算简单、精确[5]。线性规划的标准形式要求目标函数最小化、约束条件取等式，变量非负不符合条件的线性模型首先要转化为标准形，再进行求解。线性规划的求解方法有一般图解法和单纯法（Simple Method），单纯法第一次由Dantzig于1947年提出，后经学者的不断实验、改进渐趋完善。单纯法是一种迭代算法，它从所有基本可行解的一个较小部分的迭代最终产生最优解。MATLAB软件中工具箱所用到的是投影法，它实际上是在单纯法基础上的一个变形，相比于前两种方法，MATLAB的linprog函数使用的投影法，使得运算过程大大简化，避免用手算时的繁琐，提高规划的效率和精准度，能迅速地解出物流运输的最优方案。线性规划问题有求最大值和求最小值两种，在MATLAB中求解以最小值为标准形式，不符合标准的线性模型必须转化为标准形之后方能求解。

在实际的生产生活中，若能根据环境的条件要求建立准确的数学模型，一般要通过采用线性规划的手段来解决这个问题，而MATLAB软件对求解模型方面具有不可替代的作用，利用MATLAB软件中强大的分析运算能力可以大幅度提高工作效率，并且得到精确的计算结果。

3 MATLAB函数linprog在求解物流运输问题中的原理

对于一个生产企业来说，经营活动大致分为三个环节，购进原材料、制造生产以及出售给分销商，运输路径问题存在于购进原材料与运送到分销商两个阶段，一家企业可能会有不同的生产制造厂地，需要从不同的原材料供应地进货，加工以后再运往不同的收货地，面临不同的原材料供应点和市场上的收货点，同时来往不同地点耗费的成本各不相同，在这么一个复杂的系统中，企业便想找到一个最优方案从而使得运输成本最少。

求解运输的最优方案实际上是求函数中的最小值问题，linprog函数是MATLAB软件中优化工具箱中自带的函数，以目标函数最小化的标准构建，是求解线性规划问题最简单快捷的工具。用linprog函数求解线性规划问题的具体语法如下：

X=linprog（ F,A ,b）：求解问题min FX，X的约束条件为Ax≤B。

X=linprog（ F,A,b,Aeq,Be q）：求解上述问题，增加约束条件Aeq=Beq。若此约束条件不存在，那么将A=［］、b=［］。

X=linprog（ F,A,b,Aeq,Beq,lb,ub）：定义变量X的下界lb和上界ub，使得X处在此范围中。

X=linprog（ F,A,b,Aeq,Beq,lb,ub,x0）：初值定义为x0。若是大型算法则忽略初值。

［X, fval］=linprog（ F,A,b,Aeq,Beq,LB）：返回目标函数最小值fval和当目标函数取最小值时X的取值。

4 MATLAB函数linprog在求解物流运输问题中的实际应用

某水果罐头制造企业有A、B两个生产厂地，需要从I、II两个水果园进水果，还要向甲、乙、丙三个大型市场供应罐头，I水果园每次最多可提供水果量为3吨，II水果园每次最多可提供的水果为4吨；甲、乙、丙三个市场的罐头需求量分别为3吨、5吨和4吨，假设两家果园水果价格一样，每单位的水果可制造2单位的罐头，那么如何设计A、B两个厂地的运输途径才能使得运输成本最小？

根据表1、表2和图1可计算在初始方案下，运输费用f=80×1.5+50×1+60×2+70×1.5+50×2.5+60×0.5+30×2+40×3+30×2+30×2=850元。

表1 单位运费表

优化方案：针对上述结果，首先构建数学模型，建立线性方程组。设A厂地从I、II水果园分别进水果X1,X2吨的水果，B厂地分别从I、II水果园进X3,X4吨的水果；A厂地分别对甲、乙、丙供X5,X6,X7单位的罐头，B厂地分别对甲、乙、丙供X8,X9,X10单位的罐头（如表3所示）。

表2 原先运输方案

则优化后的模型中，目标函数fx=80X1+60X2+50X3+70X4+50X5+30X6+30X7+60X8+40X9+30X10。

Subject to：

图1 网络结构图

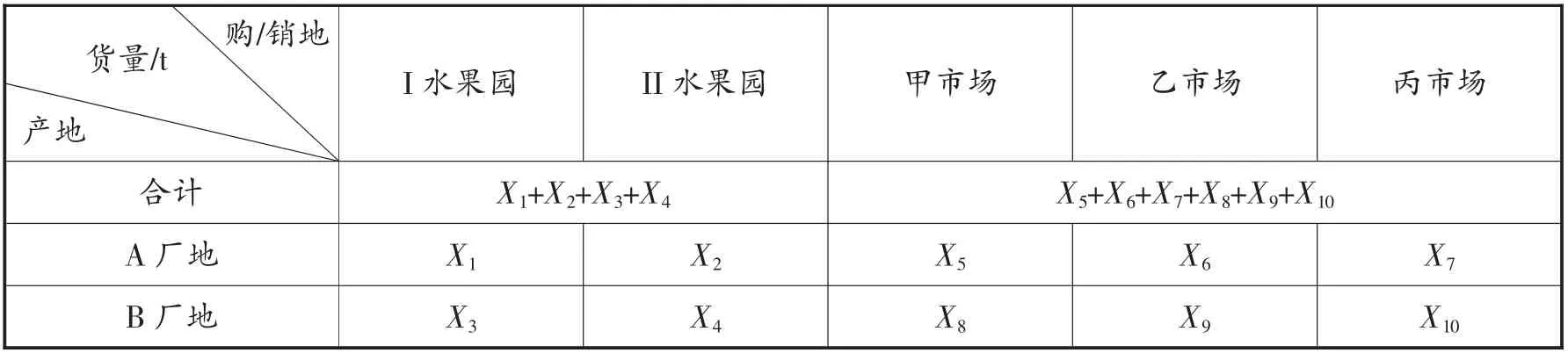
表3 假设的运输量X

等式（1）表示保证甲市场的供货量为3吨，等式（2）表示乙市场的供货量为5吨，等式（3）表示丙市场的供货量为4吨；等式（4）表示A、B两个加工厂地进的水果综合为6吨，等式（5）表示A厂地产销相等，等式（6）表示B厂地产销相等；不等式（7）表示I水果园提供的水果最多为3吨，不等式（8）表示II水果园提供的水果最多为4吨；不等式（9）表示A、B两个加工厂地从I水果园和II水果园进的水果，以及向甲、乙、丙三个市场的输送的罐头都不可能小于零。

上述10个条件变量在MATLAB中的求解过程为：

求解结果为：

由此得出优化后的模型如下：X1=0，X2=4，X3=2，X4=0，X5=3，X6=5，X7=0，X8=0，X9=0，X10=4。

如表4所示，即在优化后模型下，A厂地从从I水果园进水果0吨，从II水果园进水果4吨，供货给甲市场3吨，供货给乙市场5吨，供货给丙市场0吨；B厂地从I水果园进货2吨，从B水果园进货0吨，供货给甲市场0吨，供货给乙市场0吨，供货给丙市场4吨。此时运输费用最低为760元，相比于优化之前，节省运输成本。

表4 优化后的变量

5 结论

运输成本通常是企业考虑的重要问题，优化运输路径是企业不可缺少的工作。本文通过对罐头厂的问题分析研究，以运输成本最优为目标函数建立线性规划模型，找出影响运输路径优化的约束条件，运用MATLAB中linprog函数对模型进行求解，通过计算新的模型，最终结果显示新的路径比优化之前降低了运输费用，大大降低了企业的成本，从而为公司赢得更高的效益。从优化后的模型及结果可以知道，MATLAB软件对于解决复杂的物流运输系统的问题方面有很理想的效果。

本文只通过一个案例研究了MATLAB软件在运输路径优化的应用，MATLAB不仅在物流领域有着广泛的应用，在其他领域也有很多应用实例，除此之外很多数学工具在解决复杂实际问题中都有非常大的用途，随着社会经济以及科技的发展，追求系统化、标准化越来越成为企业的发展趋势，相信未来数学软件及方法将会在解决系统优化等的实际问题中发挥更大的作用。