危险品运输路径选择多目标优化

陈 琼，陈京荣，王 霞，张 继

（兰州交通大学 数理学院，甘肃 兰州730070）

0 引言

近年来，随着工业化的快速发展，我国对于危险品的需求日益增长。据不完全统计，我国道路危险品年运量约11亿吨，其中，95%左右的危险品都是通过公路运输的，并且每年保持约10%的增长态势[1]。危险品运输不同于一般货物运输，一旦发生事故，后果将会非常严重。例如，2017年“5·23”张石高速公路氯酸钠爆炸事故，以及2010年6月13日浙江温岭G15沈海高速槽罐车爆炸事故，不仅造成了严重的人员伤亡和重大经济损失，而且对周边的生态环境产生了难以逆转的影响。

目前，危险品运输路径问题作为一个重要的实际问题，吸引了学术界的广泛关注。关于危险品运输的研究比较多，首先是对单式运输的研究，柴获等[2]提出了采用标准差来衡量风险公平性的评价方案，设计了考虑风险分布公平的车辆调度模型，并设计了两阶段算法求解；张萌等[3]更加贴近实际，提出事故后果基于车辆实时装载量的情形，建立保守型的双目标优化模型，并用改进的ε-约束法对模型进行求解；Pradhananga[4]和Fan[5]等人分别建立了带时间窗的危险品运输路径模型和考虑路段封闭条件下的危险品运输模型，并设计了启发式算法；辛春林、张建文等[6]运用最大最小准则，建立危险品运输网络双层规划模型，并设计出启发式算法求解。杨立娟等[7]建立了静态单点多目标条件下的危险品运输优化的模型，运用灰色关联分析法从有效路径中筛选出与“绝对最优路径”关联度最大的路线；另一类是对危险品多式联运的研究，如辛春林、冯倩茹等[8]考虑时变特性的同时，对中转作业进行细化，建立时变条件下危险品多式联运的最短路径选择模型，并提出改进标号算法求解模型；黄丽霞、帅斌等[9]以运输过程中的总成本和总风险最小为目标，构建了双目标0-1线性规划模型,基于Pareto分析设计了排序算法，以获得危险品运输的非支配路径。

综上所述，国内外对运输风险和运输成本的研究较多，但对运输时间的研究较少。本文除了考虑到运输风险和距离成本以外，还将运输时间也列入考虑范围，致力于求出运输风险小，运输距离成本低，运输时间短的运输路径。

1 危险品运输风险分析

1.1 影响因素的选取

1.1.1 发生事故的概率。因为每条路段所处的具体环境、路面状况等固有属性的不同，不同的路段发生交通事故的概率也不一样。因此，路段的事故率可以取路段平均1年在每1万辆机动车中发生的事故次数，其表达式为：

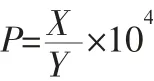
式中：P为对象路段的事故率 ［次/（年·万辆）］；X为对象路段在1年内发生的事故次数（次），Y为对象路段在1年内通过的车辆数（辆）。

1.1.2 事故敏感人数。不同路段周围环境不同，人口密度也不同。而且，不同种类的危险品发生事故后的影响范围也不一样。假设危险品泄漏后的影响面积为圆形，影响半径为d，影响范围内的人口密度为ρij，则可能受影响人数为ρij·πd2。显然，对于相同种类的危险品，排除其他不可控因素以后，决定事故后果的重要因素为路段周围的人口密度，单位为（万人·km-2）。

1.1.3 交通损失。在路径行驶过程中，由于客观原因的存在，一定的交通损失是不可避免的，可以以时间来衡量交通损失，单位为min。

1.1.4 应急救援能力。对于危险品运输来说，发生事故后的应急救援处理是非常重要的。由于危险品的特殊性质，一旦发生事故，如果处理不当，很容易造成二次事故的发生，令事故后果更加严重。因此，选用事故应急救援能力作为运输风险评价指标是合理的。本文以消防救助机构赶往事故地点所需时间为标准对应急救援能力进行评价，单位为min。

1.2 风险分析

对于静态路径网络中的路段风险，可以通过打分法来确定影响因素的值，而评估运输路段风险的影响因素的权重系数可由AHP法确定，过程如下：

Step 1：采用Saaty的1～9标度法确定比较矩阵A：

Step 2：计算权重向量，求得矩阵最大特征值与对应的特征向量（权重向量）为：

Step 3：对结果进行一致性检验，可得：

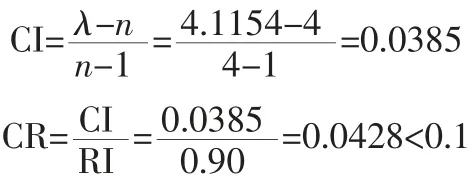
通过一致性检验，判断矩阵具有完全一致性。则用AHP法确定的风险为：，其中：为第k个影响因素的打分值。打分标准如表1所示：

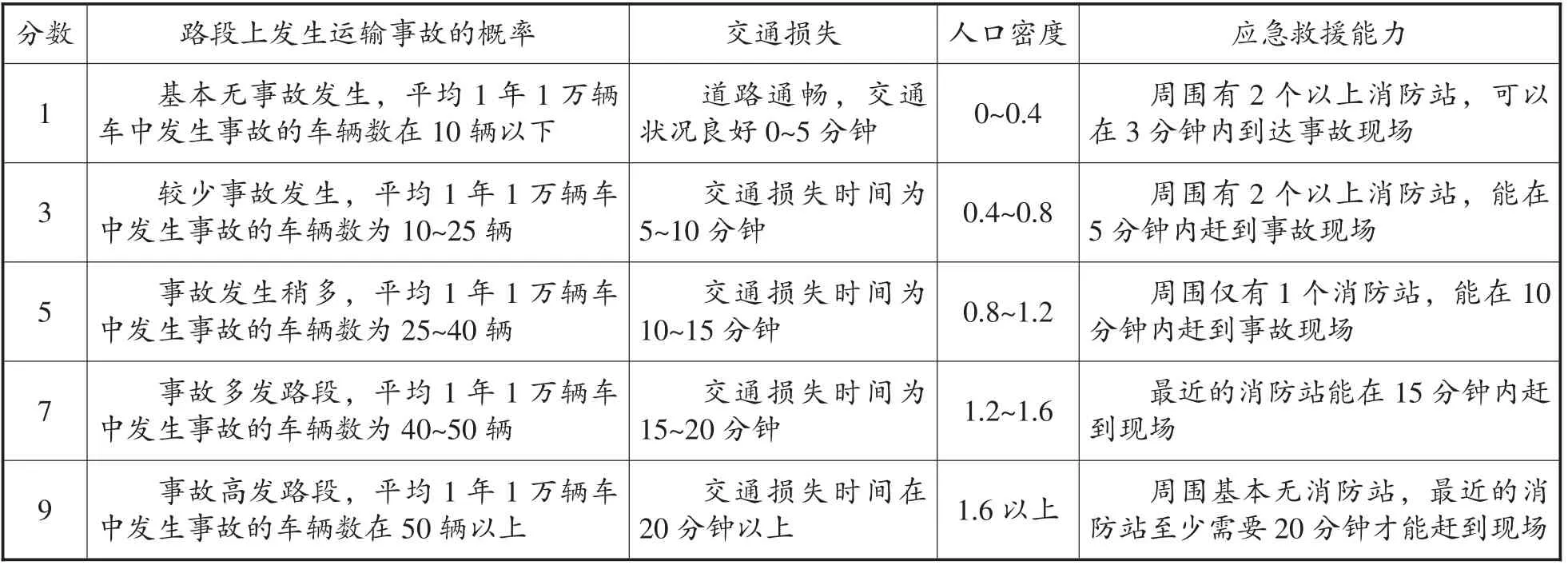
表1 路段风险影响因素评价打分表

2 数学模型

2.1 模型建立

为了避免其他因素的影响，预先做出如下背景假设：（1）运输危险品的车辆均为专用车辆，且运输车的载重量在不可超重且符合道路载重量的前提下尽量满足客户需求；（2）所有车辆均以道路允许的速度行驶，且互不相容的危险物品不在同一时间由同一车辆运输；（3）各个路段的风险值可以进行累加，总路径风险值即为路径上的各路段风险值相加。

为了便于模型描述与建立，首先给出建模所需的决策变量：

目标函数：

约束条件：

其中：式（4）为起点约束；式（5）为中间节点约束，保证运输过程中不会有环的出现；式（6）为终点约束。

2.2 模型分析与求解

危险品运输路径优化问题，实质上是比较特殊的多目标优化问题。对于多目标优化问题来讲，由于各个目标之间存在互相冲突的情况，无法在保证某一个目标取得最优值的情况下同时不削弱其他目标的最优值，所以基本不存在绝对最优解。对于危险品运输路径优化问题，综合考虑，应该找出综合属性最优的危险品运输路径。

求解步骤：

Step 1：分别求出以最短运输距离、最小运输风险以及最短运输时间为单目标的最优路径，如果3条路径相同，则该路径即为绝对最优路径，算法结束；否则，转步骤2。

Step 2：求出路段的综合属性值。

Step 2.1：确定路段综合属性中的权重向量。利用层次分析法对路段的3个属性进行分析，确定其权重向量为

Step 2.3：为了消除量纲对结果的影响，预先对属性值矩阵进行规范化处理，得规范化矩阵，其中：

Step 3：以路段的综合属性值为测度，求解最短路径，可得从起点到终点的综合最优路径。

3 实例验证

以某地区的运输网络为例，寻求某易燃物品从起点1运输至终点6的综合最优路径。运输网络如图1所示。

图1中各个有向弧对应的属性值如表2所示。

根据求解步骤，求得最小运输风险对应的路径为1→3→5→6，最小运输风险为5.68；

最短运输距离对应的路径为1→2→4→6，最短运输距离为28；

最短运输时间对应的路径为1→3→5→4→6，最短运输时间为35；

绝对最优路径不存在，转Step 2。

Step 2：规范化决策矩阵，求出所有路段的综合属性值。

Step 3：以综合属性值为测度，求起点到终点的最短路径。

经过计算，整理可得最优路径为1→3→5→6，综合属性值为7.513，它的属性向量为（5.68,34,41）。

4 结论

本文从危险品运输路段发生事故的概率、人口密度、交通损失及事故应急响应能力等方面综合分析评估危险品运输路段上的风险，以最小化运输风险、最小化运输距离及最小化运输时间为目标建立了优化模型，并针对该模型设计了求解算法，最后运用实例验证了求解算法的可行性，说明合理的评估危险品运输风险和科学的路径选择优化不仅可以有效地减少危险品运输事故发生的风险，还可以节约运输成本，减少运输时间。

图1

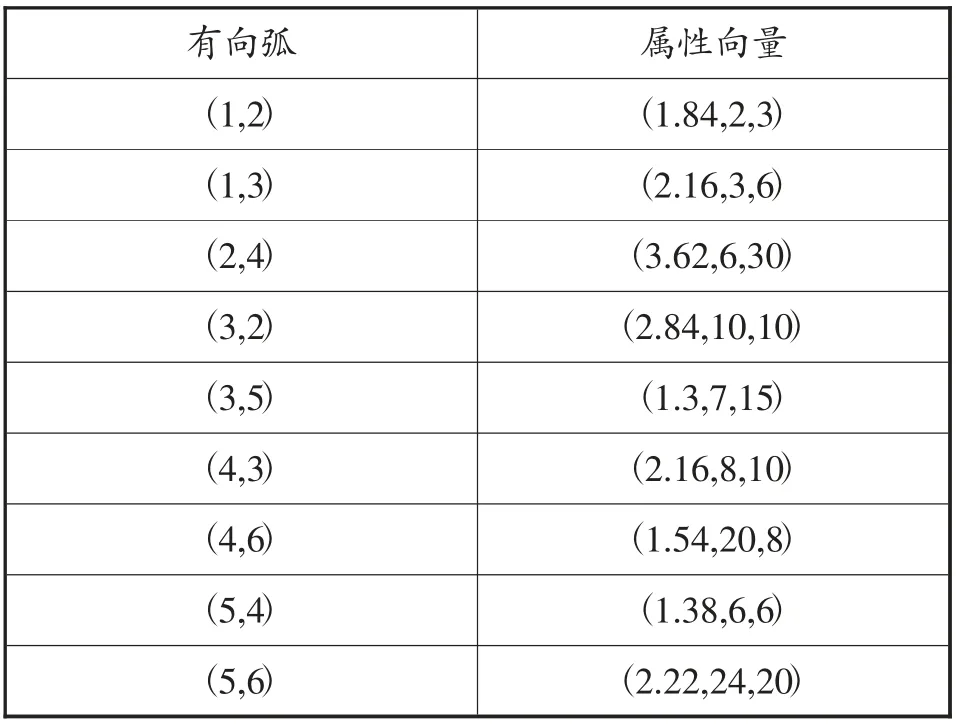
表2

但是本文所进行的研究也有所局限，本文仅研究了静态网络下的危险品运输路径选择问题，实际情况下某路段的运输网络中的风险和交通情况是随机变化的，对于动态时变网络中的危险品运输路径选择优化问题需要进一步的研究。