齿轮公法线长度参数化计算模型的研究与应用

谢仁华，管嫦娥*，林 通,2

(1.江西应用技术职业学院 机械与电子工程学院， 江西 赣州 341000；2.浙江理工大学 机械与自动控制学院， 浙江 杭州 310018)

齿轮传动因传动精度高、结构紧凑等诸多优点应用十分普遍[1]。在加工齿轮的过程中，经常要测量齿厚，以此评定齿间侧隙是否合理，能否保证精确传动[2]。常用的齿厚测量方法有弦齿厚测量法、跨棒距(即M值)测量法和齿轮公法线测量法[3]。齿轮公法线测量法不以齿顶圆为定位基准，对齿顶圆精度要求不高，也不用借助量棒或量球，操作简单，精度高，因此应用甚广[4]。齿轮加工后要检测公法线实际长度是否合格，首先要确定评判的标准，即齿轮公法线长度的工艺参数值。目前齿轮公法线长度工艺参数值的确定方法有以下几种：文献[5]直接利用齿轮公法线公式计算确定，涉及函数多，计算繁琐，容易出错；文献[6-7]利用CAXA软件，采用图解的方法得到齿轮的公法线长度，不同的齿轮参数需绘制不同的图形，绘图过程复杂，效率太低；文献[8]开发了基于VB和SQL Server的齿轮公法线计算程序，该方法要求有较强的VB语言编程能力。

本文通过剖析齿轮公法线长度的计算原理，利用常用的机械设计软件Creo的参数化建模和测量功能，模仿其计算状况，实现齿轮公法线长度参数化计算模型的构建。该计算模型相对文献[5-8]所述方法，建模过程简单，无需额外VB语言编程，适用于不同参数齿轮的公法线长度计算，不仅直观实用，而且精度更高[9]。

1 齿轮公法线长度计算原理及计算公式

齿轮公法线长度计算原理如图1所示。从图中可以看出，齿轮公法线长度W(即线段AB)等于一个基圆齿厚加上k-1个基圆齿距，其中k为测量时的跨齿数[10]。根据渐开线的形成原理，可知发生线分

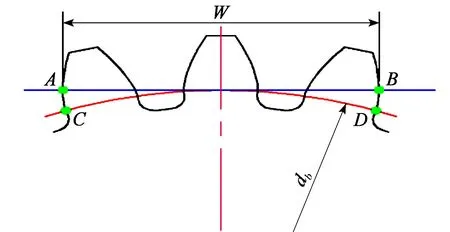
图1 齿轮公法线长度计算原理

Wk=mcosα[π(k-0.5)+zinvα]+2xmsinα，

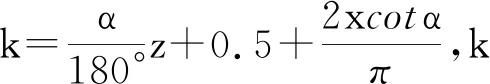
2 Creo参数化建模的基本原理

Creo具有强大的参数化建模功能，是专业的CAD/CAM/CAE应用软件。在利用Creo进行三维造型时，会自动生成基于特征的Program，它会记载所有特征的创建步骤，如尺寸、参数及关系式等各种信息。

通过Program，可以方便地实现Creo的二次开发。开发时三维模型的设计步骤不用重复编写，只须根据需要增加相关的指令，输入参数值就能方便地得到一系列和原模型特征相似的模型，从而达到参数化设计的目的。

3 齿轮公法线参数化计算模型的构建

由齿轮公法线长度计算原理图(图1)可知，齿轮公法线长度W等于线段AB的长度，该线段同基圆相切，与所跨轮齿外侧渐开线相交。所以，可以运用Creo建模功能，构建齿廓曲线和齿轮公法线长度线段AB的参数化模型，同时用草绘中的“相切约束”功能，让线段AB同基圆db相切，从而构建齿轮公法线参数化计算模型，明显其和使用公式计算的几何模型毫无差别。构建参数化计算模型的流程如图2所示。

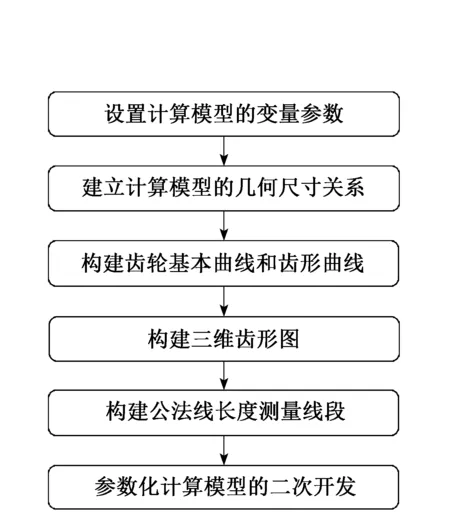
图2 参数化计算模型构建流程

3.1 设置计算模型的变量参数

构建齿轮公法线参数化计算模型时，主要相关的变量有[12]：模数M、齿数Z、压力角ALPHA(α)、变位系数X、顶隙系数CX、齿顶高系数HAX、跨齿数K、齿宽B。执行面板命令：模型→模型意图→参数，建立如图3所示的变量参数表，并同时赋初始值。

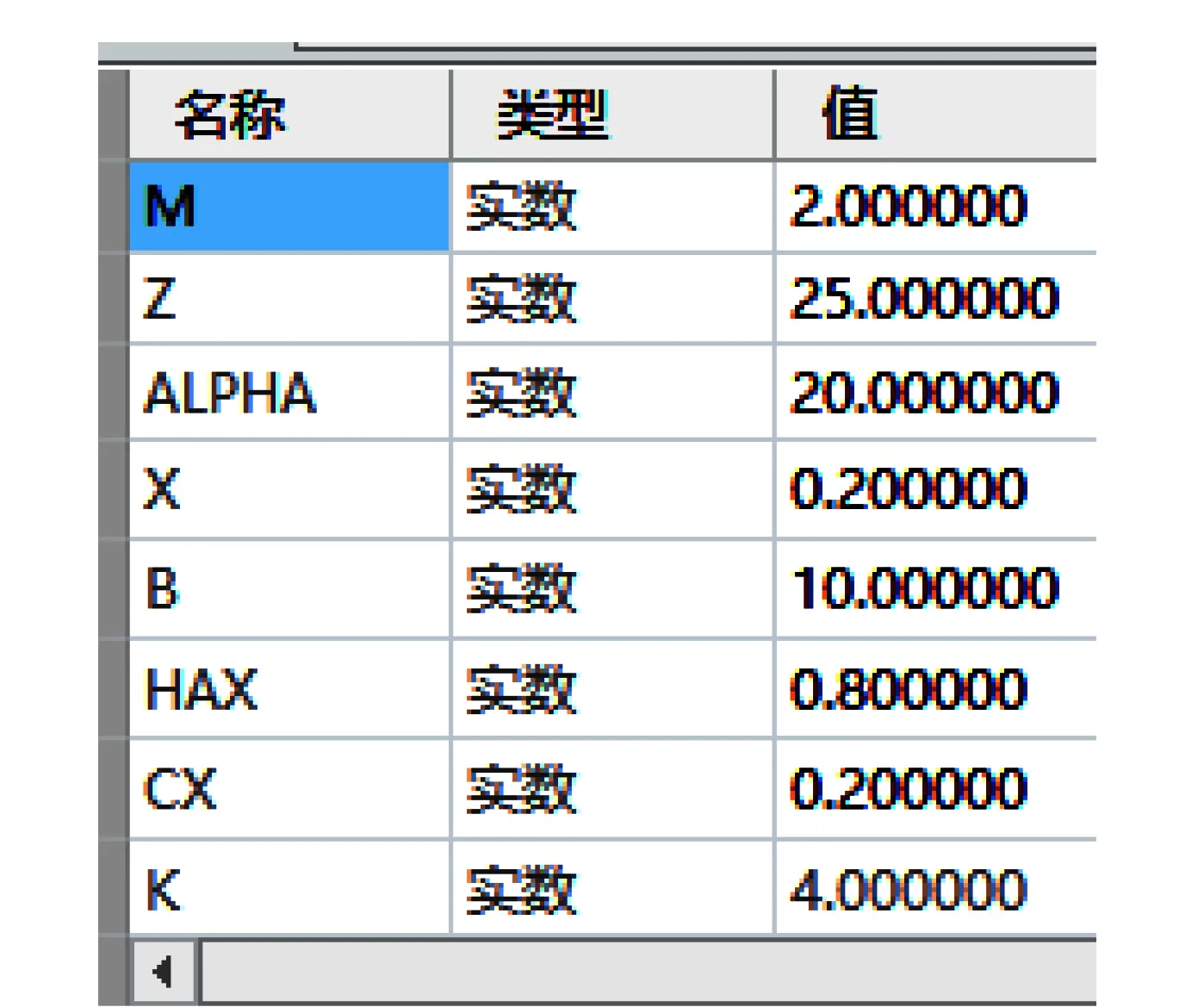
图3 变量参数表

3.2 建立计算模型的几何尺寸关系

执行菜单命令：模型→模型意图→关系，定义尺寸符号与参数间的关联性，将以下关系式输入至对话框中：

D=M*Z

DB=D*cos(ALPHA)

DA=D+2*M*(HAX+X)

DF=D-2*M*(HAX+CX-X)

3.3 参数化计算模型的构建

3.3.1 构建齿轮基本曲线

图4 齿轮基本曲线和齿廓渐开线曲线

新建一零件文件，执行菜单命令：模型→草绘，用绘图命令绘制基圆、分度圆、齿根圆、齿顶圆等基本曲线[13]，如图4所示。

3.3.2 构建渐开线齿形曲线

执行菜单命令：模型→基准→曲线→来自方程的曲线→方程。将以下渐开线方程输入自动弹出的编辑窗口中：

R=DB/2

THETA=T*45

X=R*cos(THETA)+R*sin(THETA)*THETA*PI/180

Y=R*sin(THETA)-R*cos(THETA)*THETA*PI/180

Z=0[14]

3.3.3 构建三维齿形图

将齿根圆沿轴向拉伸5(B值)，同时将渐开线a与b，齿顶圆、齿根圆(利用草绘中的投影获取)进行修剪，得到独个齿形曲线，将独个齿形曲线拉伸5，得到独个齿的三维特征，如图5中所示的齿1。将齿1进行轴类型阵列，阵列数为1，成员间阵列角度为(360°/z)×(k-1)，得到齿2。

3.3.4 构建齿轮公法线长度测量线段

以图5所示的三维齿形的实体表面为草绘平面，绘制一线段MN，线段两端点M、N分别约束在齿1、齿2外侧齿形曲线上，同时使用“相切约束”功能，使线段MN与基圆db(如图5中的粗线圆所示)相切，此时线段MN的长度就等于齿轮公法线长度W。隐藏齿轮基本曲线，最终的参数化计算模型如图6所示。

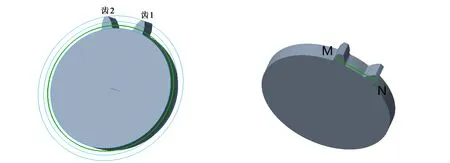
图5 三维齿形图 图6 齿轮公法线长度测量线段

3.4 参数化计算模型的二次开发

为使参数化计算模型具有广泛的适用性，即能计算不同参数齿轮的公法线长度，须对该模型进行二次开发。执行菜单命令：模型→模型意图→程序→编辑设计→自文件，将会自动打开Program设计程序，对程序进行相应的修改。

在INPUT和END INPUT之间输入以下语句：

M NUMBER

"请输入模数："

Z NUMBER

"请输入齿数："

ALPHA NUMBER

"请输入压力角："

X NUMBER

"请输入变位系数："

B NUMBER

"请输入齿轮宽度："

HAX NUMBER

"请输入齿顶高系数："

CX NUMBER

"请输入顶隙系数："

在RELATIONS与END RELATIONS之间输入以下关系式：

SD0=D /*分度圆直径

SD1=DB /*基圆直径

SD2=DA /*齿顶圆直径

SD3=DF /*齿根圆直径

D5=B /*齿轮宽度

D6=0.46*M /*齿根倒圆角半径

K=ALPHA*Z/180+0.5+2*X*cot(ALPHA)/PI /*初算跨齿数

K=ceil(FLOOR(2*K))/2 /*四舍五入后的跨齿数

P23=1 /*阵列成员数

D7=(360/Z)*(K-1) /*阵列成员间角度

程序修改完成后，单击保存，会自动弹出“要将所做的修改体现到模型中”的确认对话框，选择“是”即可。至此，二次开发的参数化模型就构建完成了。

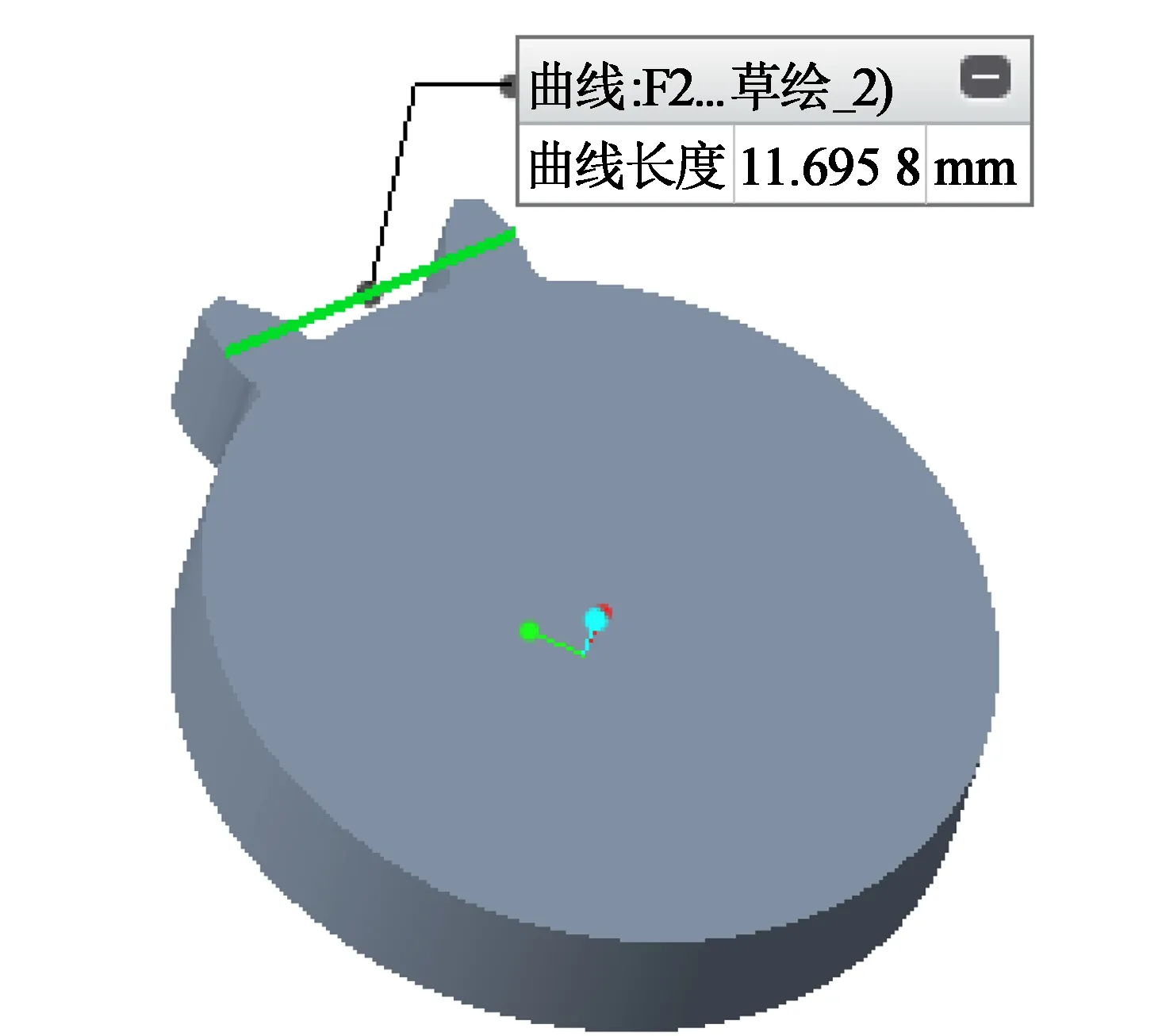
图7 齿轮公法线长度测量值

4 参数化计算模型的应用

构建好参数化模型，就可以使用它计算齿轮公法线长度，采用表1的第一组数据进行计算。

执行菜单命令：模型→重新生成，会自动弹出“得到输入”菜单，选择“输入”选项后，将弹出“INPUT SEL”菜单,选择“全选”选项并确认后，将依次询问模数、压力角、齿数、变位系数等变量参数值。依次输入各个参数值后，将自动更新参数化模型。

执行分析→测量→长度，选择被测对象(线段MN)，将自动得到被测线段的长度，如图7所示，其数值11.695 8 mm便是齿轮公法线的长度值。

5 模型测量值与公式计算值的分析与比较

采用同样的操作方法，将表中第2、3组的模数、齿数、压力角、变位系数、顶隙系数和齿顶高系数等参数值分别输入至参数化计算模型中，可得到齿轮公法线的长度值分别为21.529 0及22.575 5。将模型计算结果同公式计算值进行分析比较，情况如表1所示。

表1 齿轮公法线长度值分析对比表

从表中可以看出，两者非常接近，虽具有一定的差异，但差值非常小，不到0.001 mm，完全符合齿轮公法线长度值的精度要求。由此表明，构建的齿轮公法线长度参数化计算模型精确，完全符合工艺要求。

6 结论

(1)构建了齿轮公法线长度计算的参数化模型，该模型能方便计算不同参数的齿轮的公法线长度。

(2)实例应用表明，该参数化计算模型精确度高，完全满足工艺要求。

(3)模型计算值与公式计算值，两者存在细微差异，主要是因为公式计算中应用了余弦函数cosα、正弦函数sinα、渐开线函数invα及无理数π，客观上会造成精度损失而导致的，但计算模型采用参数化建模，不会产生精度损失，因此精度更高。