某型飞机起落架防扭臂结构轻量化设计

王 琨，赵知辛,2*，汪 杰，薛旭东

(1.陕西理工大学 机械工程学院， 陕西 汉中 723000；2.陕西省工业自动化重点实验室， 陕西 汉中 723000)

飞机起落架是一种能够实现飞机起飞、降落、滑跑、停放的主要装置，是保证飞机安全飞行的重要结构，因此对飞机起落架进行结构设计就显得尤为重要。对飞机来说，减少自身的重量意味着油耗量的减少，油耗量的减少也会降低排放量。因此，如何在满足强度与刚度的要求下，减少飞机起落架的自重已成为目前飞机领域中的研究热点。随着计算机辅助工程(CAE)技术的快速发展，传统的由设计师凭借自身知识和经验，进行人工反复迭代的过程，已经远远不能满足当下飞机结构的设计需求，因此迫切需要一种新方法来对飞机起落架进行轻量化设计。

国内外已经有研究者将拓扑优化技术、尺寸优化技术运用到对飞机、汽车的结构设计中。如刘文斌等[1]基于变密度法，建立了某型无人机的三维模型，采用拓扑优化的方法，获得了无人机在典型工况、多种约束条件下的最佳拓扑优化结构，并对无人机优化前后的结构性能加以对比，优化后的结构减重明显。焦洪宇等[2]将主梁优化域分成若干个子域，建立起子域与优化域之间的联系，并对横梁进行了拓扑优化，各子域出现孔洞，获得了具有类似“桁架式”结构的拓扑形式。BRADEN T等[3]发现后机身双引擎飞机舱壁能够将发动机引起的振动传播到乘客舱，对其进行了拓扑优化，能够减少舱壁结构的质量，消除发动机激振频率10%的共振。邓扬晨等[4]为了研究歼击机水平尾翼大轴的结构设计，利用工程梁理论对其进行了建模，然后采用近似函数与黄金分割法对其进行了尺寸优化，优化后的结构减重效果明显。宋凯等[5]提出了一种适用于汽车概念设计阶段的车身T型接头优化方法，并采用最小二乘响应面方法建立了接头的优化模型，运用连续二次规划方法对其进行了优化。郭策等[6]将一种新型的仿甲虫鞘翅轻质结构应用于飞机大开口区的筋板结构设计，并利用响应面优化的方法对其进行了尺寸优化，优化后的结构减重明显，且散热性能与抗压刚度都明显改善。LIU Jie等[7]使用拓扑优化技术，以体积作为约束条件，以飞机扰流器的刚度最大为目标，对传统的飞机扰流器进行了优化，最后得到了一个重量较轻的三明治结构。由于起落架结构较为复杂，目前很少见到将拓扑优化方法或尺寸优化方法运用到对飞机起落架的结构设计中，且上述学者都是在设计过程的某一阶段采用了一种优化技术，虽然优化效果也很明显，但很难说达到了最优设计。

本文针对某型飞机起落架防扭臂结构，在实际工况条件下先对防扭臂结构进行静力学分析，然后通过拓扑优化方法对防扭臂结构进行开槽和钻孔设计，最后再利用响应面优化方法，在满足强度和刚度的条件下，以防扭臂槽深和孔的直径作为设计变量，以质量作为目标函数，对防扭臂结构进行进一步的尺寸优化。

1 防扭臂结构有限元分析

1.1 防扭臂优化模型的建立

飞机起落架防扭臂结构由上下防扭臂以及3个销轴构成，由于防扭臂是将活塞杆所受的扭矩传递到减震支柱的外筒上，为了更好地模拟实际工况，故建立了减震支柱的外筒、活塞杆、上下防扭臂、3个销轴的三维模型。上防扭臂通过销轴连接在缓冲器的外筒上，下防扭臂通过销轴与活塞杆相互铰接，上下防扭臂通过中间销轴铰接。材料为40CrMnSiMoVA,强度极限为1760 MPa，弹性模量为200 GPa，泊松比为0.3。

1.2 约束及载荷

飞机在起飞、降落、滑跑、停放的过程中，由于地面高低不平，会使飞机起落架左右颠簸，左右颠簸的力会使缓冲器中的活塞杆承受扭矩，该扭矩会通过销轴传到下防扭臂，然后通过中间销轴传到上防扭臂，最后再通过上销轴传到缓冲器的外筒上，故上下防扭臂主要是阻止内外筒相对转动。因为上防扭臂是通过销轴与减震支柱的外筒相互铰接，而外筒是固定不动的，则在上防扭臂两端施加固定约束，并在活塞杆上施加大小为10 687 N·m的扭矩，如图1所示为约束与载荷的施加情况。

1.3 扭矩理论计算

飞机起落架布局图如图2所示。

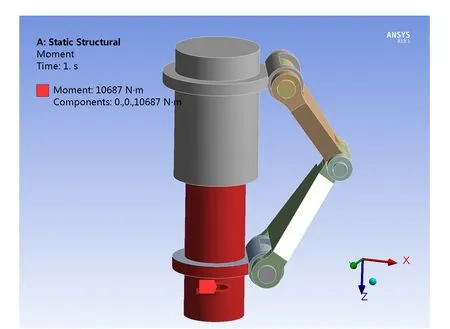
图1 防扭臂结构的约束及载荷

图2 飞机起落架布局图

1.3.1 飞机起落架性能参数[8]

着陆设计重量：WL=12 800 kg；

着陆设计重量重心位置：h=1.634 m,a=6.343 5 m,b=0.928 5 m；

最大设计起飞重量重心位置：H=1.52 m,a=6.419 m,b=0.853 m；

主轮距：t=3.741 m；

前主轮距：a+b=7.272 m。

1.3.2 对称着陆载荷

(1)当量重量

Wm=0.5WL=6400 kg。

(2)着陆功量

(3)着陆垂直载荷

主起落架(支柱式起落架)轮胎压缩取最大压缩的50%,

δu=0.5δmax=0.5×0.13=0.065 m。

缓冲器行程

Su=0.9Smax=0.9×0.36=0.32 m,

ny,m=k1×k2×ny,u=1.1×1.05×1.78=2.06。

(4)两点水平着陆主起落架载荷

最大垂直载荷情况

py,m=ny,m×Wm×g=2.06×6400×9.81=129 335 N,

Fx,m=-0.4py,m=-51 734 N。

最大起转情况

py,m=ξ1×ny,m×Wm×g=0.55×129 335=71 134 N,

Fx,m=-0.8py,m=-56 907 N。

防扭臂与缓冲支柱计算简图如图3所示。

图3 防扭臂与缓冲支柱计算简图

扭矩

MT=Fx,m×L×sin70°=56 907×0.2×sin70°=10 687 N·m。

上述公式中Vy为飞机下沉的速度，L为轮轴的长度，k1、k2均为放大系数，ny，u为使用功垂直过载，ny，m为主起落架的垂直过载，η为缓冲器效率系数，ξ1为起转载荷系数。

1.4 仿真结果与分析

本文主要研究的是上下防扭臂，故只查看上下防扭臂的变形及应力分布情况，图4、图5分别为上下防扭臂的变形情况与应力分布情况。

从图4可以看出最大变形量约为0.7 mm，防扭臂的变形比较小，这说明防扭臂的刚度冗余很大，有很大的改进空间和轻量化设计空间。从图5可以看到最大等效应力为556.73 MPa，出现在上下防扭臂靠近边缘的部位，且中间部位所受应力很小，因此可以考虑在上下防扭臂的中间区域开槽、钻孔。

2 拓扑优化

2.1 变密度法拓扑优化

传统的设计师一般是通过在实际工况下对上下防扭臂进行应力分析，然后在防扭臂所受应力较小的区域中，再对上下防扭臂进行开槽和钻孔，这种方式不仅不精确，而且对设计师的要求很高。

对防扭臂进行开槽、钻孔，减重孔、减重槽以及无开槽区域对应三种不同的厚度ei(i=1，2，3)，因此对防扭臂进行开槽钻孔，可以等效为平面中不同刚度的材料布局问题[9],如图6所示。

图4 防扭臂的变形云图 图5 防扭臂的等效应力云图

图6 平面多刚度结构

选取上下防扭臂为设计区域，将设计区域划分为无限个单元，每个单元的相对密度ρ作为设计变量，只允许设计变量取离散值0、α、1，0<α<1，但离散值之间的组合特别多，这会使得优化过程难度加大，故将离散的设计变量放松为连续的设计变量，采用SIMP法，孔、槽的厚度可以用下式来计算：

Y=ρh，

E=ρAE0,

式中Y为厚度变量，ρ为单元设计变量，h为防扭臂的厚度，E为设计变量ρ对应的杨氏模量，A为惩罚因子，E0为A=1时的杨氏模量。当A>1时会对中间厚度进行惩罚，就会减少中间厚度区域(开槽区域)，当A=1时不对中间厚度进行惩罚，即中间厚度区域不会减少。

2.2 拓扑优化数学模型的建立

在此次拓扑优化中，把单元相对密度作为设计变量，结构的最小柔度作为目标函数，以结构的体积作为约束条件，则可建立如下的数学模型[10-11]：

Findρe,e=1,2,…,m,

s.t.KU=F,

0<ρmin≤ρe≤ρmax≤1,e=1,2,…,m,

式中ρ为单元设计变量，C为结构的柔度，F为载荷矢量，U为位移矢量，K为结构刚度矩阵，ve为单元体积，ue为节点位移矢量，f为保留的体积分数，ρmin为设计变量的取值下限，ρmax为设计变量的取值上限,v为设计变量都为1时的体积。

2.3 优化模型的求解

拓扑优化是在原结构设计的基础上确定出最优的拓扑分布形式，优化后的结果如图7所示，可以看出：

(1)拓扑优化后的结果中，需去掉的材料区域比较清晰，但形状不太规则，这使得防扭臂的制造加工难度加大，因此需要对拓扑优化的结果进行调整；

(2)材料去除的区域主要集中在上下防扭臂的中间部分，形成了明显的开槽区域；

(3)一些部位优化结果不太理想，例如去掉了下防扭臂的双耳和单耳部分，这会使得上下防扭臂之间无法再通过销轴连接起来，也无法传递活塞杆上的扭矩，所以应该对Remove(0.0～0.4)区域的材料进行合理的优化。

2.4 防扭臂的结构参数模型

由于在选择设计域时，将防扭臂的双耳及单耳部分也包括在内，故双耳及单耳部分有些地方也被去除。考虑到防扭臂的吊耳起到连接上下防扭臂、活塞杆以及缓冲器外筒的作用，因此不去除吊耳部分的材料，而是根据拓扑优化结果在防扭臂中下部区域进行大面积双面开槽及钻孔，上下防扭臂槽深均为8 mm、孔直径均为30 mm。对该结构进行静力学分析，图8为优化后防扭臂结构的等效应力分布情况，表1为防扭臂前后优化性能的对比。

图7 拓扑优化结果云图 图8 优化后上下防扭臂的等效应力

表1 优化前后最大等效应力、最大变形、质量的对比

由表1可以看出优化后防扭臂的最大等效应力为997.9 MPa，与优化前的应力相比增加了79.2%，优化后的应力值仍小于材料的强度极限。优化后的变形量为0.866 mm，与优化前的变形量相比增加了22.1%，但优化后防扭臂的质量减少了18.4%，这表明轻量化效果明显。

3 防扭臂结构优化设计

3.1 结构优化响应面模型的建立

通常使用二次多项式函数形式的一阶或二阶响应面模型来近似表示设计变量与目标函数之间的关系。采用二次多项式响应面模型表达式如下[12-13]：

一阶响应面模型的基本形式为

二阶响应面模型的基本形式为

式中a0、ai、aij为未知参数，将它们按照一定顺序排列就可以构成列向量a，xi为设计变量。

3.2 优化数学模型

结构优化问题可以被定义为在一定的约束条件下，选取合适的设计变量X={x1,x2,…,xn}，使目标函数达到最优。针对防扭臂的结构，考虑到要减轻防扭臂的质量，而防扭臂的质量主要是取决于双面槽的深度与孔的直径，所以选取上下防扭臂槽深P1、P2、P3、P4与开孔直径P5、P6作为设计变量，在满足防扭臂强度与刚度的条件下，以防扭臂的质量最小为目标，对防扭臂进行优化。其数学模型为[14-15]

minM=f(X),

s.t.A≤1760 MPa,B≤1.5 mm,

xmin≤xi≤xmax,i=1,2,…,n,

式中M为防扭臂的质量，A为最大等效应力，B为最大变形，xmin为设计变量的下限值，xmax为设计变量的上限值。各设计变量参数如表2、图9所示。

表2 各设计变量的取值范围

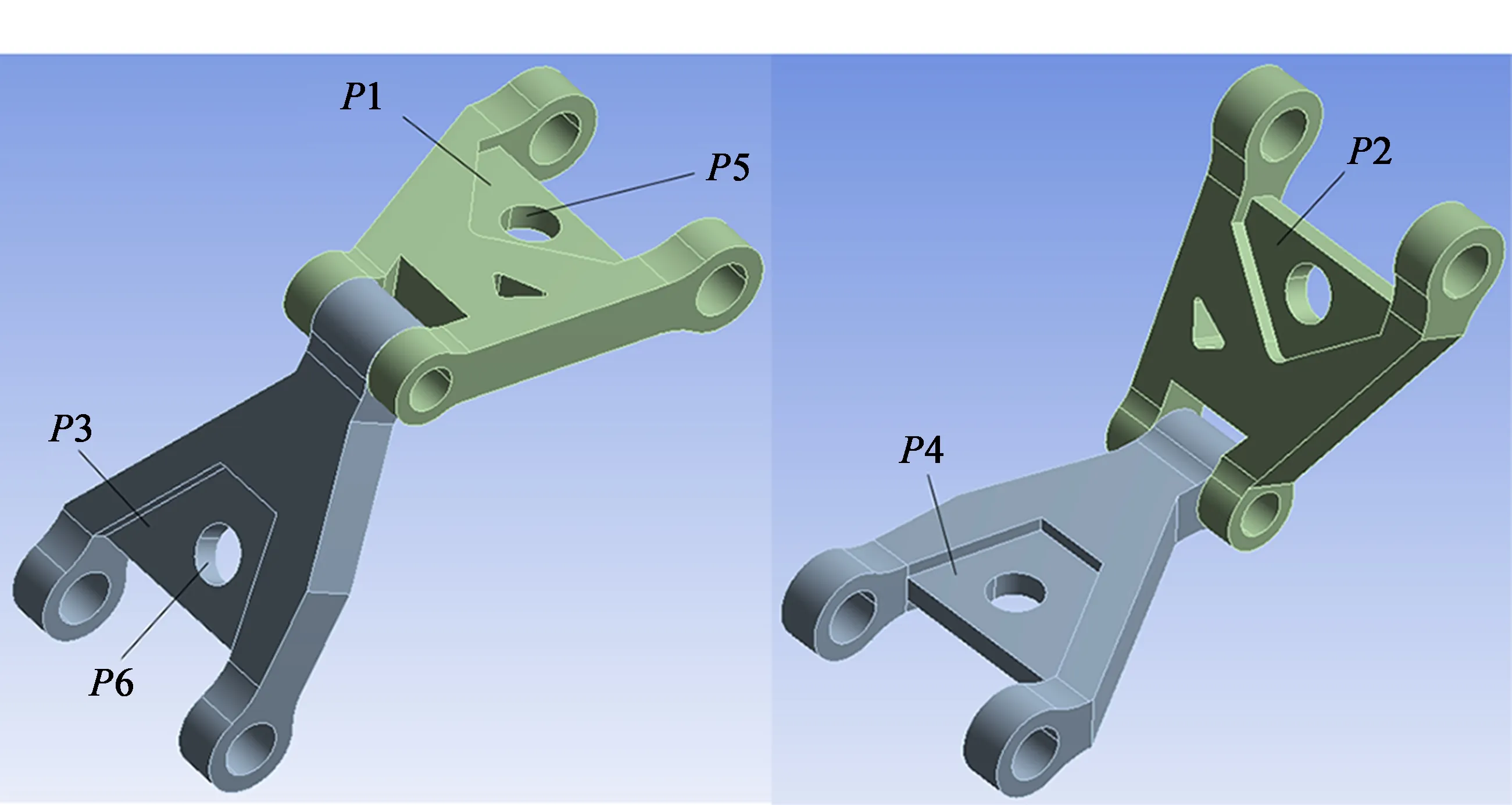
图9 防扭臂槽深、圆孔的参数

3.3 优化结果

优化后的结果如表3所示，图10、图11为优化后防扭臂的整体变形与等效应力云图。

表3 防扭臂结构优化前后结果对比

由表3可知，优化前防扭臂所受最大等效应力为997.90 MPa，优化后为998.14 MPa，提高了0.02%，优化后应力值仍符合强度要求。从图11可以看到最大应力出现在上下防扭臂开槽的边缘处，这符合预期。

由表3可知优化前防扭臂最大变形为0.866，优化后最大变形为0.865，仅仅下降了0.11%，可以看出该优化方法对防扭臂刚度无太大改变，因此此次优化是在保证强度和刚度的条件下，对防扭臂进行了合理的优化。

由表3可以看出优化前防扭臂的质量为7.593 kg，优化后的质量为7.200 kg，减少了5.17%，这说明轻量化效果明显且材料得到了充分利用。

图10 优化后整体变形云图 图11 优化后等效应力云图

4 结论

(1)讨论了防扭臂的实际受力情况并通过计算得到了在实际工况下防扭臂所受的扭矩大小，然后对防扭臂结构进行了静力学分析，得到了防扭臂结构的变形与应力分布云图。

(2)在满足防扭臂强度与刚度的条件下，对防扭臂结构进行了拓扑优化研究，获得了容易加工的防扭臂最优拓扑结构形式，优化结果中质量减少了18.4%，轻量化效果明显。

(3)在拓扑优化的基础上，采用响应面优化方法，以防扭臂中槽深、圆孔直径为设计变量，在满足强度与刚度的要求下对防扭臂结构进行了尺寸优化，优化结果中质量减少了5.17%，等效应力提高了0.02%，刚度变化不大。

(4)通过拓扑优化与尺寸优化两种方法使防扭臂质量共减少了22.6%，且得到了更优的防扭臂结构，这对飞机起落架其他部件的优化提供了一定的参考价值。