一种2自由度并联偏转平台的动力学分析

徐慧茹，陈 纯，王佳伟

(陕西理工大学 机械工程学院， 陕西 汉中 723000)

与串联机构相比，并联机构具有结构稳定紧凑、承载能力强、无累计误差、精度较高等优点引起了国内外学者的广泛关注，其中并联机构的动力学建模是实现其高速、高精度运动控制的前提条件[1-4]。在总结并联机构动力学分析目标的基础上，典型的动力学研究方法主要有牛顿-欧拉法、拉格朗日法和凯恩法等，其中根据系统的动能和势能建立的基于虚功原理的拉格朗日法，推导过程简单且得到的动力学方程在形式上相对简洁，并且能够清楚地表达各构件之间的耦合关系[5-7]。现今许多国内学者都对不同类型的并联机构进行了动力学研究[8-11]。朱伟等[12]运用虚功原理建立了SCARA并联机构的动力学模型，通过仿真验证了动力学模型的正确性。王潇剑等[13]以一种2UPU/SP并联机构为研究对象，建立了该3自由度并联机构的运动学模型，并基于虚功原理，推导了动力学模型，给出了一种动力学性能评价指标。张军等[14]以3-PPR并联机构为研究对象，运用拉格朗日方程法和虚功原理建立了该机构的动力学模型，并通过仿真验证了动力学模型的正确性。

本文基于球面二自由度并联机构原型，设计了一种结构新颖的2自由度并联偏转平台，因其动平台独特的偏转运动，故主要应用在大型游乐设施或模拟军事训练中。

1 机构描述

球面2自由度并联机构又称空间五杆机构，该机构所有运动副皆为转动副，且其轴线都相交于一点[15]。该机构的特点是两个驱动电机放在同一平面内固定，两电机主轴轴线相互垂直，两轴线的交点与运动副轴线的交点重合皆为机构的球心，动平台只做围绕球心的旋转运动。本文基于球面2自由度并联机构的结构特点设计一种能使动平台同时绕X、Y轴两个方向上偏转±45°的平台。

在SolidWorks中建立并联偏转平台的模型，如图1所示。该平台主要由机座11、驱动架9、凸形驱动架3、驱动环2以及各销轴组成，其中固定在凸形驱动架3上的两个销轴4以及固定在驱动环2上的两个销轴7构成四点共同承担动平台5的偏转运动，以保证平台偏转时结构稳定。凸形驱动架3通过角接触球轴承(图中未标出)和销轴4由转动副与动平台5连接，驱动环2通过角触球轴承(图中未标出)和销轴7由转动副与动平台5连接。驱动环左侧、驱动架右侧分别通过固定在他们自身上的销轴与机座连接，限制了两个销轴的自转与驱动环2、驱动架9的轴向移动。驱动架9与凸形驱动架3通过销轴8连接，驱动架左侧和驱动环右侧分别安装在电机10、1的主轴上，电机10、1固定在机座上。当两个电机启动时，各驱动支架和销轴带动动平台5实现同时绕X、Y轴两个方向上±45°的偏转，且平台偏转时各构件不会产生干涉。该平台的材料属性如表1所示。

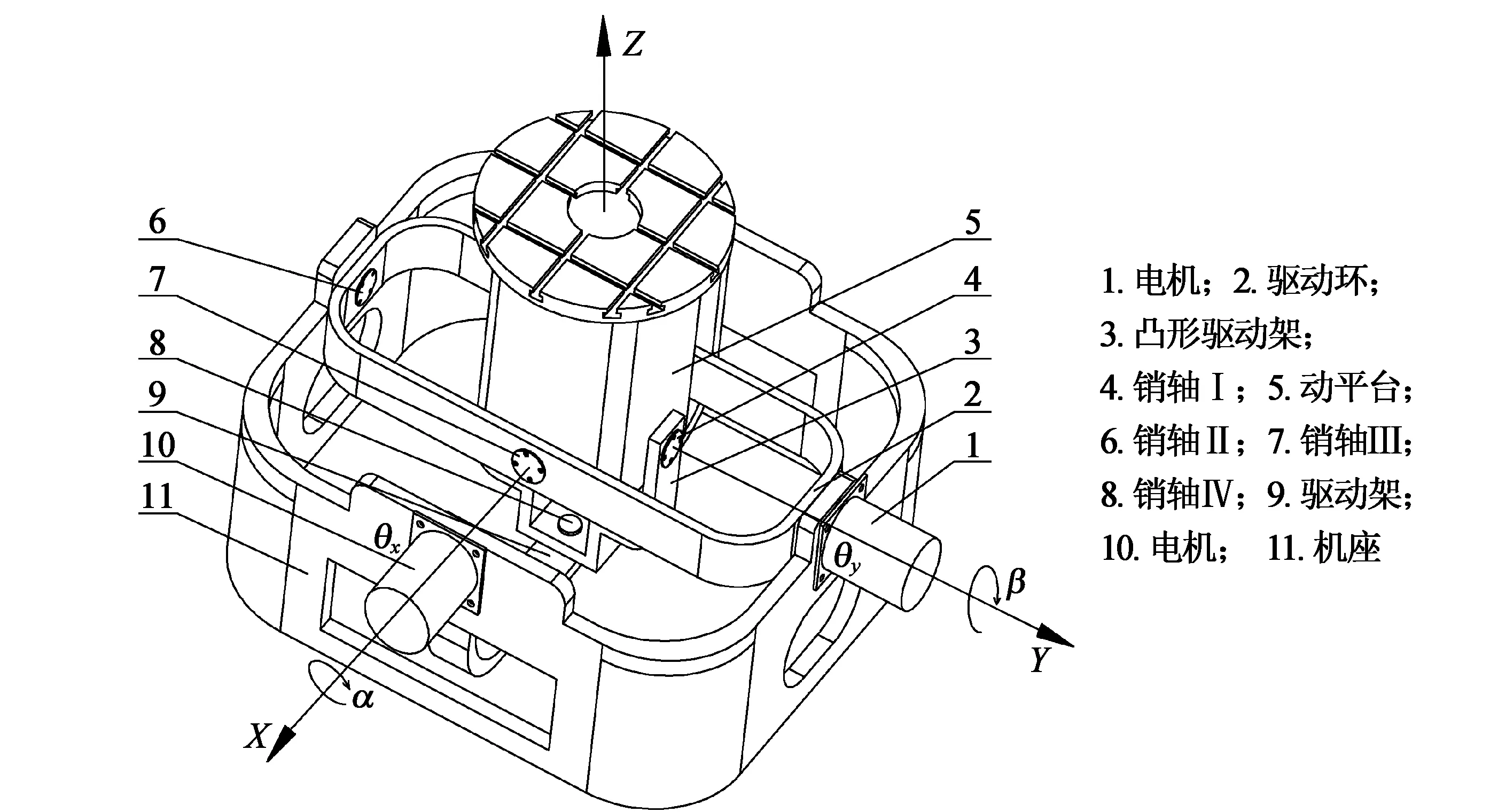
图1 并联驱动偏转平台模型

表1 材料属性参数

2 输入输出运动方程

如图1所示，驱动电机10、1的输入角度分别为α和β，动平台5绕X、Y轴的输出角度分别为θx和θy。现已知动平台5绕X、Y轴的偏转角度分别为θx和θy，来反解出驱动电机10、1的偏转角度α、β。

安装在电机1主轴上的驱动环2被其驱动，通过销轴7使动平台5绕Y轴偏转了θy，将动平台在绕Y轴方向上的位置偏转简化成如图2所示的空间几何关系，可知驱动环2绕Y轴的偏转角度等于动平台5绕Y轴的偏转角度，所以动平台在绕Y轴偏转时的位置解为

β(t)=θy(t)。

(1)

安装在电机10主轴上的驱动架9被其驱动，而凸形驱动架3通过销轴8与驱动架9连接，通过凸形驱动架上的销轴4使动平台5绕X轴偏转了θx，所以驱动架9绕X轴的偏转角度并不等于动平台5绕X轴的偏转角度。假设在驱动环2偏转θy度的前提下，当动平台绕X轴的偏转角度为θx时，此时驱动架9绕X轴的偏转角度并不是θx，而是θx1。将动平台在绕X轴方向上的位置偏转简化成如图3所示的空间几何关系。

由图3可得

(2)

将θx1=α代入式(2)得

α(t)=arctan(tanθx(t)cosθy(t))，

(3)

将式(1)、(3)整理成矩阵形式

(4)

从式(4)中可以看出，驱动电机1的偏转角度只与动平台5绕Y轴的角度θy有关；而驱动电机10的偏转角度不光与动平台5绕X轴的角度θx有关，还与其绕Y轴的角度θy有关，二者之间存在耦合关系[16]。

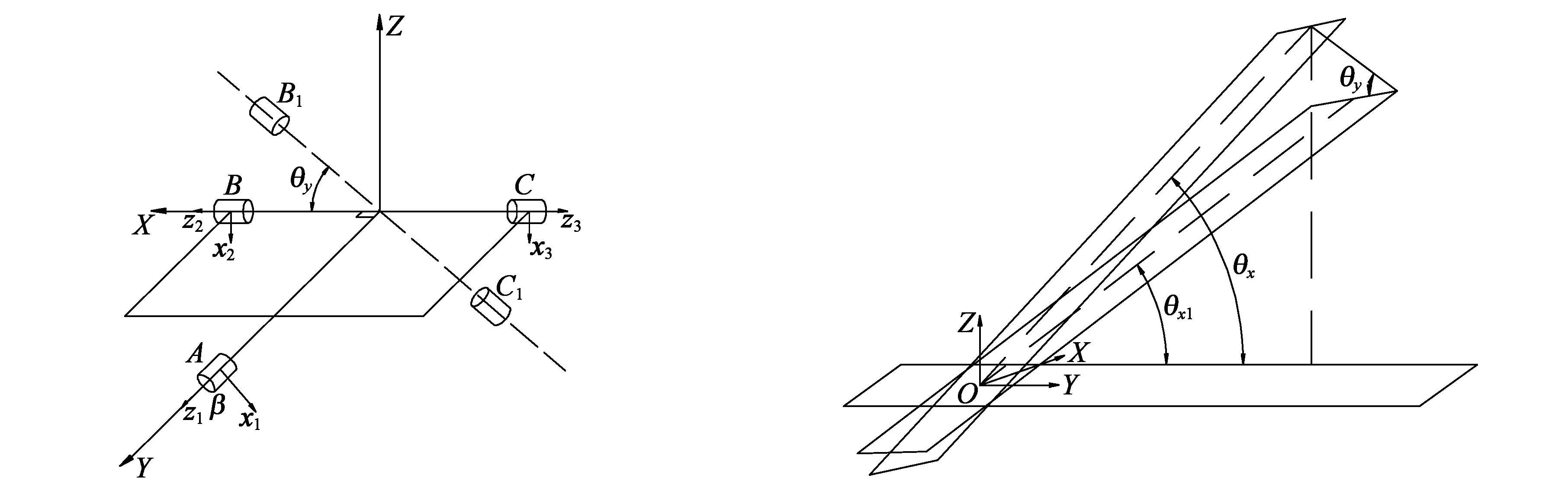
图2 绕Y轴偏转示意图 图3 绕X轴偏转示意图

对上述平台的位置逆解分析中得到的平台位置方程(4)求其对时间的一阶导数可得该平台的速度逆解，即

(5)

则该平台的速度Jacobian矩阵为

(6)

3 动力学建模

对该平台进行动力学分析时，采用拉格朗日方法建立其动力学模型。该方法从系统的动能出发(势能为0)，推导步骤简单，建立的拉格朗日方程形式简便易求解[17]。利用动力学方程，结合平台的位置方程、速度Jacobian矩阵和动能方程，在给定动平台的运动规律情况下，可反解出两个驱动电机的输出力矩。

3.1 动能方程

平台总动能T可表示为

T=T1+T2，

(7)

式中T1为当平台绕X轴偏转时，驱动架、凸形驱动架、动平台的动能，T2为当平台绕Y轴偏转时，驱动环和动平台的动能。

动能T1的表达式为

(8)

(9)

动能T2的表达式为

(10)

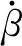
(11)

故可得平台总动能：

(12)

3.2 平台的广义坐标与广义力分析

由机构自由度的概念可知，机构具有确定运动时所给定的独立参数的数目等于机构的自由度数目，此时的独立参数又称为广义坐标。该平台共有2个转动自由度，因此需要2个独立参数。为了求得广义坐标qk下的广义力Qk，不妨设一个广义坐标qk不为零，另一个广义坐标qk为零，则根据虚功原理可得

QkΔqk=∑δW′=MΔφ+MkΔqk(k=1,2)，

(13)

其中

M=Mxi+Myj+Mzk,

Δφ=Δφxi+Δφyj+Δφzk,

φ=(θx,θy)T，

式中Mx、My为在X、Y两个方向上动平台所受外力矩，Δφx、Δφy为动平台绕X、Y两个方向上的偏转角度，Mk为驱动电机的输出力矩。

对式(13)两边同除Δqk，得

(14)

整理式(14)可得

(15)

(16)

3.3 非保守系统下的拉格朗日方程

该平台非保守系统下的拉格朗日方程为

(17)

将式(12)代入式(17)中，可求解出：

(18)

(19)

(20)

(21)

(22)

(23)

将式(19)、(20)、(22)、(23)代入式(17)，得

(24)

(25)

将式(24)、(25)代入式(16)得平台的动力学模型为

(26)

4 动力学仿真与数值算例

为了验证所建立的平台动力学模型的正确性，现给出平台的参数和所受附加力矩，利用Adams软件对其进行动力学分析，将虚拟样机仿真得到的电机输出力矩值和理论值对比，验证平台在给定运动状态下电机的力学特性。利用SolidWorks软件测得平台各构件的转动惯量，I1=56 952.947 kg·mm2，I2=18 650.464 kg·mm2，I4=77 127.60 kg·mm2，Ixx=126 697.17 kg·mm2，Ixy=-2 658.23 kg·mm2，Iyx=-2 658.23 kg·mm2，Iyy=116 689.93 kg·mm2。

为了更加直观了解平台动力学模型的特性，在Adams软件仿真中加入扰动项，可使所模拟的环境更贴合工程实际。假设动平台所受附加外力矩为Mx=5.0 N·m、My=5.0 N·m，动平台绕X、Y轴的运动输入分别为

(27)

根据所给定的平台参数、平台所受外力矩和速度函数，利用Adams软件对平台进行动力学分析，得到驱动电机10、1的输出力矩M1、M2的曲线图，如图4所示。

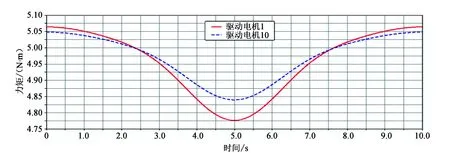
图4 输出力矩曲线图

从图4中可知，当动平台的运动输入确定时，电机1的输出力矩M2在全时刻下的相对力矩均比电机10的输出力矩M1大，与上述运动学的结论一致，验证了该平台理论分析的正确性。当动平台受到绕X、Y轴的同等外力矩时，驱动电机10、1输出的力矩M1、M2在全时刻下的最值差异不大，故可知该平台具有良好的动力学性能，这为实际工况下的操作过程减少了难度。

为了进一步验证平台动力学模型的正确性，根据该平台的动力学模型式(26)可计算出两个驱动电机的输出力矩，将计算所得的电机输出力矩和Adams软件仿真所得的进行比较，如图5、图6所示。

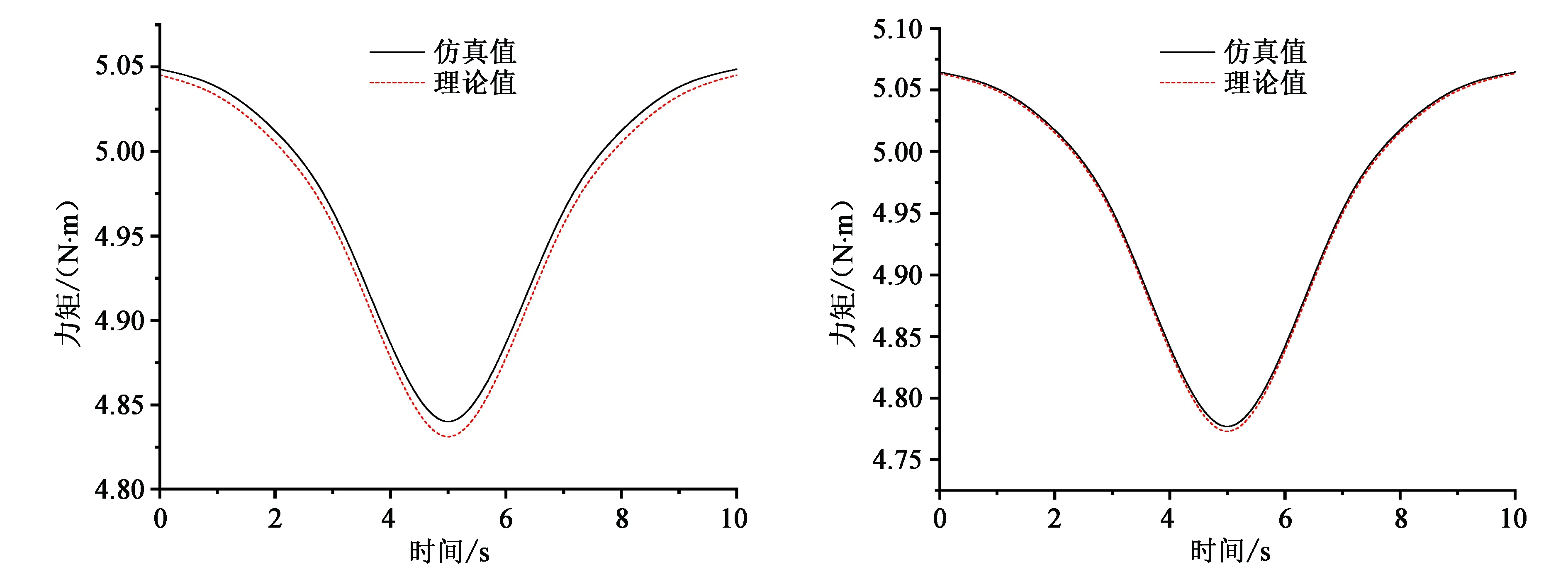
图5 电机10输出力矩对比曲线图 图6 电机1输出力矩对比曲线图

在上述两个图中分别取电机10和电机1的输出力矩最小值，进而计算出所得理论值与仿真值的相对误差，从而进一步验证该平台动力学的正确性。驱动电机10的最小输出力矩M1min的仿真值与理论值分别为M1min_f=4.840 1 N·m，M1min_l=4.831 1 N·m。驱动电机1的最小输出力矩M2min的仿真值与理论值分别为M2min_f=7.777 0 N·m，M2min_l=7.773 1 N·m。

则两个驱动电机的最小输出力矩的相对误差为

由上式结果可知，通过软件仿真和理论计算所得到的力矩相对误差比较小，进一步验证了该平台理论分析的正确性。

5 结论

根据该偏转平台的几何和运动特性，求解出了平台的位置逆解方程和速度雅克比矩阵。通过对该平台模型的简化，得到了平台的总动能，并利用非保守系统下的拉格朗日方程和虚功原理建立了该平台的动力学模型，在特定外力矩和运动输入情况下求解出了电机的输出力矩。运用Adams软件对该平台进行了动力学分析，通过仿真结果和理论结果的对比，求解出了电机的最小输出力矩的相对误差，均较小，进一步验证了理论分析的正确性，并为后续研究相关类型的并联机构奠定了基础。