福建省高精度水平速度场模型构建与评估

杜仲进

（福建省测绘院，福州 350003）

0 引言

由于地壳运动和形变等因素引起的站点坐标变化对现代毫米级大地测量技术具有很大的影响，测站高精度坐标必须通过速度场归算到用户所需的历元时刻才具有工程实用价值。速度场的拟合目前除了使用NNR-NUVEL1A[1]模型，主流方案是利用近几十年来采集的中国大陆空间大地测量数 据求取速度场。

自2011 年12 月中国大陆构造环境监测网络即陆态网（crustal movement observation network of China， CMONOC）完成全部建设任务后，CMONOC便成为推算中国大陆或局部区域速度场的主要数据源[2-5]。常用的速度场模型建立方法主要分为欧拉矢量法和数值拟合法：欧拉矢量法分为整体、块体和局域欧拉矢量法[6-8]，其中局部欧拉矢量法精度最高，可达到1～2 mm/a 的精度[9]。数值拟合方法有多种，常用的有临近点插值、反距离插值、克里金插值、最小曲率法、三角网插值和多面函数插值等方法，其中临近点和反距离插值法原理最为简单，但仅考虑距离作为权重标准不太合理[10-11]；最小曲率法是构造1 个具有最小曲率的非精确曲面，需要经过迭代处理[12-13]；克里金法考虑了随机数据的期望和方差等信息，适用性较广且精度通常较高，但原理复杂，特别是半变异函数的选取直接影响到结果的精度[14]；多面函数法是采用一系列单值数学面叠加逼近某一曲面，精度较高，但核函数和光滑系数的选择还是要具体问题具体分析[15-16]；三角网法原理简单，在考虑了速度和方位信息的同时，可以刻画更为精细的局部特征，因此插值精度高，适用性广[12]；另外，采用数值拟合方法得到格网速度场，使用更为简便。

考虑到沿海区域速度场模型的数据现势性、高精度性和简单适用性原则，本文基于福建省及周边区域测站2011—2017 年近7 a 的观测数据进行处理分析，利用局部优化过程（local optimization procedure， LOP）三角网反距离加权格网模型构建福建省区域格网模型，并讨论了区域欧拉矢量模型的应用。

1 基于GAMIT/GLOBK 的福建CORS 数据解算

CMONOC 主要由均匀分布在全国的260 余个连续运行参考站（continuously operating reference stations， CORS）和2 000 余个不定期观测区域站构成。为了研究福建省及周边地区水平速度场模型，本文选取CMONOC 中位于福建省及其周边地区的7 个CORS 和68 个区域站进行速度场解算和分析。其中，CORS 观测数据收集大多起始于2010—2011 年，总体时间跨度约7～8 a，区域站观测数据为2009 年以后的数据，复测频率定为 每2 年1 次。研究区域的站点分布如图1 所示，圆形代表区域站，三角形代表CORS。

本文采用 GAMIT/GLOBK 软件处理福建省及周边区域的站点观测数据，为了将同全球卫星导 航 系 统(global navigation satellite system， GNSS）测站同国际GNSS 服务组织(International GNSS Service， IGS）站进行联合解算，还需选取国内及周边的17 个IGS 站（AIRA、BJFS、DAEJ、IISC、IRKT、KIT3、KUNM、LHAZ、PIMO、POL2、SHAO、URUM、WUHN、YSSK、TIXI、ARTU和TCMS）进行约束。受计算机软件和硬件性能的限制，采用GAMIT 软件进行基线解算时，一般要求测站数量不超过60 个，否则会大大降低基线解算效率，因此首先将福建省及周边的测站按照区域划分原则分为2 个分区，加上17 个IGS约束站，每个分区测站数不超过55 个；设置好基线解算参数进行解算，得到每个分区的单日松弛解文件，然后采用GLRED 软件将全球IGS 单日解与各个分区的单日解文件进行合并，合并时仅保留稳定的IGS 核心站，需剔除出现粗差的测站信息，合并后得到包含全球IGS 核心站和福建省及周边区域测站的坐标、卫星轨道和极移等参数的单日整体松弛解；最后将所有的单日整体松弛解法方程文件进行网平差，解算福建省及周边区域测站在国际地球参考框架2014（international terrestrial reference frame， ITRF2014）下的坐标和速度。绘制研究区域测站的速度场，如图 2所示。

图2 福建省及周边区域速度场矢量图

2 福建省速度场模型的构建原理

2.1 局部地区欧拉矢量模型

由于福建省所占区域不大，且地表内部构造活动不剧烈，因此可以把整个福建及周边区域地表当作1 个刚性块体，根据欧拉定理[13]可得

式中：V为块体内某站点的速度；Ω为该站点所处块体的欧拉矢量；R为站点的位置矢量。式（1）改写成便于计算的公式[13]为

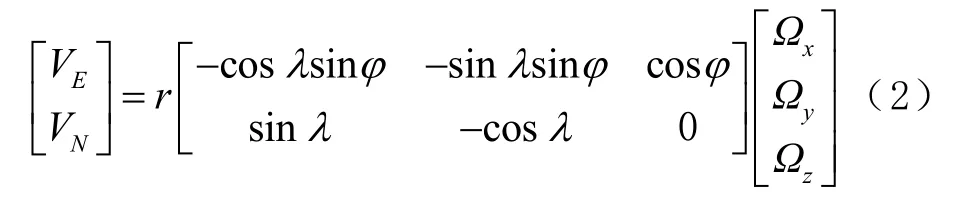
式中：VE、VN为某测站的站心坐标速度，假设块体运动沿水平方向与VU无关；r 为地球平均半径，约为6 371 393 m；λ、φ为该测站的经纬度，单位为弧度；Ωx、Ωy、Ωz为欧拉矢量的3 分量。

设欧拉矢量的估值为参数向量 ˆX ，站点的水平速度观测向量L，观测误差向量为Δ，误差矩阵为V，则可以组成误差方程为

上述方程的最小二乘解为

以福建省及周边区域测站的坐标和速度代入上述方程进行平差解算，为避免粗差对参数解算的影响，需进行迭代最小二乘计算，每次解算后以3 倍中误差准则判断数据集中是否含有粗差，直至不再含有粗差时结束迭代，得到研究区域的欧拉矢量参数。

2.2 Delaunay 三角网反距离加权法构建区域格网速度场

2.2.1 格网点生成

以115～121°E、23～28°N 为矩形边界框，以0.5°为格网间距进行格网划分，得到福建省及周边区域的经纬度格网点。

2.2.2 Delaunay 三角网生成

进行德洛奈（Delaunay）三角剖分，必须要满足2 个重要准则：唯一性和最大化最小角特性。根据Delaunay 三角网的实现过程的不同，通常分为逐点插入法、三角网生成法、分治算法和合成算法等[17]。其中逐点插入法原理简单，易于编程实现，基本步骤为：1）建立包含所有离散点集的多边形凸包；2）在构成凸包的所有点中，初始化凸包三角网；3）根据局部优化过程局部优化过程（local optimization procedure， LOP）算法优化初始凸包三角网；4）在已生成的三角网逐点插入其余散点，每次插入1 个点后，用LOP 算法重新生成三角网；5）重复步骤4），直到所有点插入完毕。

由福建省及周边区域的测站生成的Delaunay三角网如图3 所示。

图3 福建省及周边区域测站三角网

2.2.3 反距离加权法求取格网点的水平速度值

1）判断格网点位于某一三角形中。采取射线法判断1 点是否在区域内，具体步骤为：从该点向左引水平扫描线，遍历计算该射线与每1 个三角网边界的相较次数，如果为奇数，则认为在三角形内，若为偶数，则在三角形外部。如果格网点不位于三角网内部，则寻找离其最近的3 个测站点。

2）反距离加权法计算格网点水平速度场。设空 间 待 插 值点 为 P ( xp， yp， zp)，P 点 所在 邻 域 内 有3 个已知离散点 Qi( xi， yi， zi)（ i =1， 2， 3， xi、 yi，为位置信息， zi为属性信息）。根据离散点的值，通过反距离加权法对P 点的属性zp进行插值，即

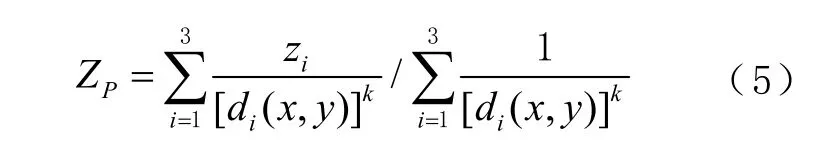
3 福建省速度场模型的精度分析

3.1 欧拉矢量模型内外符合精度分析

将福建省及周边区域当作1 个刚性块体，使用68 个区域站的坐标和速度，根据式（4）用迭代最小二乘法求取该区域的欧拉矢量，与文献[6]利用“地壳网络工程”1999—2008 年的观测数据解算的速度场模型（CHINA-2008）进行比较，具体参数见表1。根据解算得到的欧拉矢量估值计算福建省区域的欧拉矢量模型速度场残差值，如图4 和图5 所示。

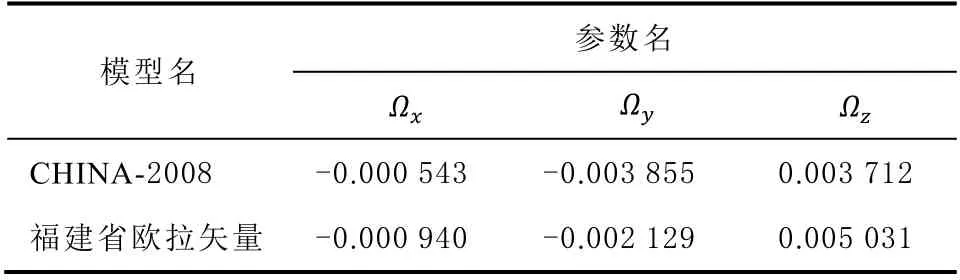
表1 福建省区域欧拉矢量参数 单位： rad/Ma

分析表1 可得：2 套参数的整体旋转趋势有较大的相似性，但是CHINA-2008 模型代表的是中国整个大陆地区的整体欧拉矢量，反映的是整个大陆运动趋势；而福建省欧拉矢量是针对局部区域构建的，因此更适合表达福建省自身块体近年来的运动趋势。因此2 套参数必然会产生一定的偏差。

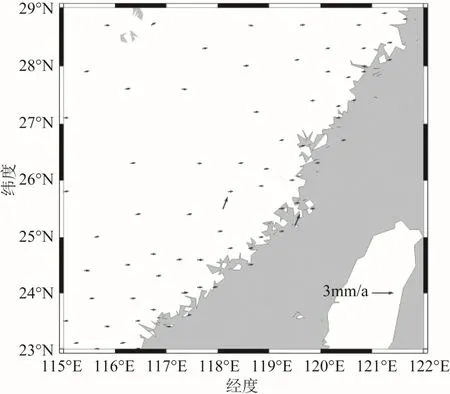
图4 福建省欧拉矢量模型区域站速度场残差矢量图

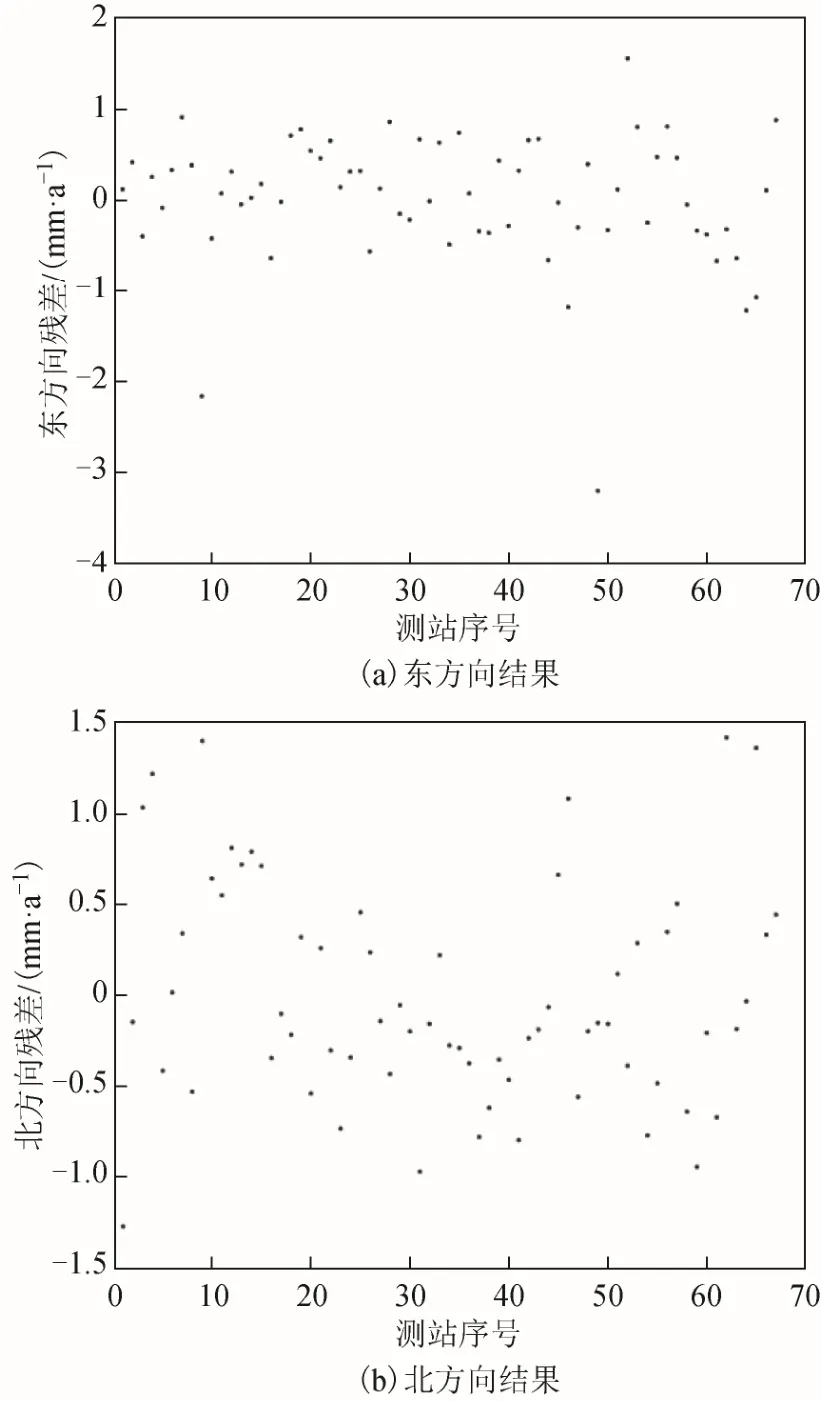
图5 福建省欧拉矢量模型区域站速度场残差散点图

分析图4 及图5 可得，采用福建省区域欧拉 矢量模型可以明显减弱该区域块体的运动趋势，除个别测站的速度残差值较大，出现该现象可能是该测站的实测速度不准造成的。经欧拉转换后，福建省区域测站点的速度残差在2 mm/a 以内，大部分在1 mm/a 以内。扣除福建省区域欧拉矢量模型后，该区域仍具有由西向东的微小运动趋势。

为了进一步验证福建省区域欧拉矢量模型的精度和可靠性，以该区域的8 个CORS 作为外部检核点，使用解算得到的欧拉矢量参数计算检核点的水平速度，并与原始实测速度作差得到残差值，如图6 所示：外部检核点残差绝对值不超过1 mm/a，其中大部分测站的速度残差表现为正向偏差，说明解算得到的欧拉矢量参数存在一定的系统性误差，该误差可能是由于部分测站的实测速度不准造成的。

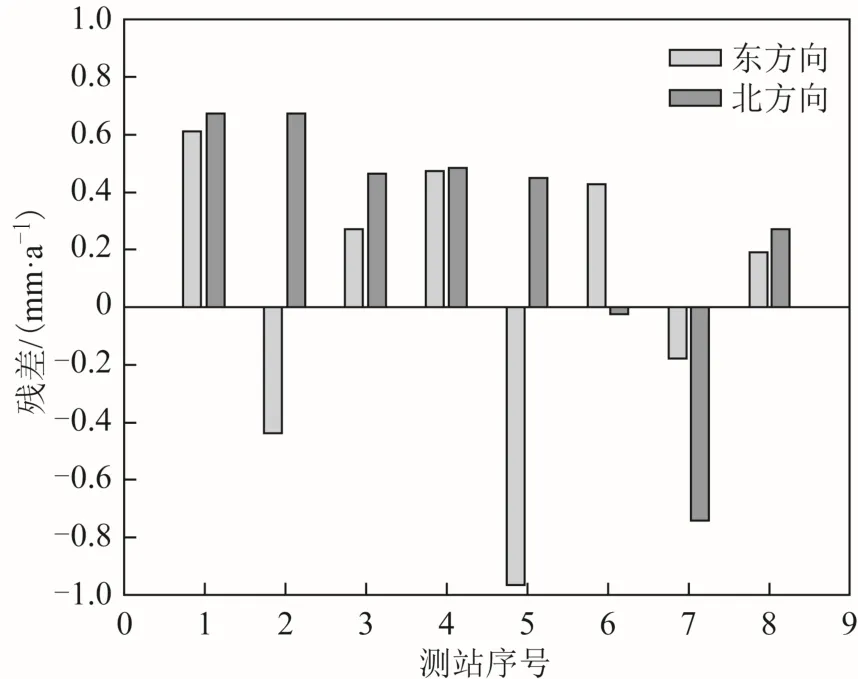
图6 福建省欧拉矢量模型CORS 速度场残差柱状图

统计福建省欧拉矢量模型的内外符合精度指标，如表2 所示。

表2 福建省欧拉矢量模型速度场残差统计 单位: mm/a

分析表2 可得，东、北方向的内外符合速度残差绝对值在0.5 mm/a 左右，东（E）、北（N）方向的内外符合速度残差中误差均不超过1 mm/a，区域站残差绝对值的最大值超过3 mm/a，而CORS残差绝对值的最大值不超过1 mm/a，说明区域站速度场精度低于CORS 速度场精度。总体来看，区域站内符合精度与CORS 站外符合精度保持在同一精度水平上，福建省欧拉矢量模型东、北方向均能达到1 mm/a 的精度。

3.2 Delaunay 三角网反距离加权格网速度场模型内外符合精度分析

在福建省及周边区域内，使用68 个区域站的经纬度坐标构建三角网，并基于反距离加权原理计算每个格网点的水平速度值，如图7 所示。根据解算得到的欧拉矢量估值计算福建省区域的欧拉矢量模型速度场残差值，如图8 所示。

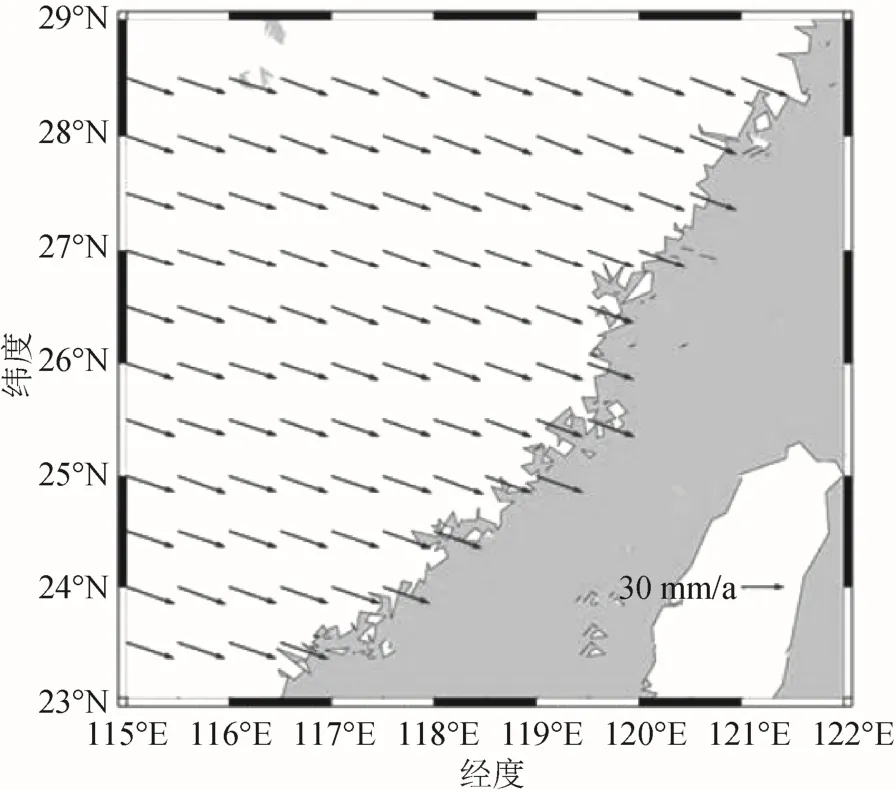
图7 福建省区域格网速度场矢量图

图8 福建省三角网模型区域站速度场残差散点图

分析图7、图8 可得，采用三角网反距离加权模型得到的格网速度场整体具有西北至东南的运动方向，整体测站平均运动速度为：E 方向32.8 mm/a，N 方向-11.7 mm/a。根据格网速度场反推区域站的速度值并与实测值作差得到速度场残差值，福建省区域测站点的速度残差在2 mm/a 以内，大部分在1 mm/a 以内。同样，为了进一步验证福建省区域三角网反距离加权模型的精度和可靠性，以该区域的8 个CORS 作为外部检核点，使用区域格网速度场计算检核点的水平速度，并与原始实测速度作差得到残差值，如图9 所示，外部检核点残差绝对值不超过1 mm/a。

统计福建省区域格网模型的内外符合精度指标，如表3 所示。分析可得与欧拉矢量模型较为一致的结果，东、北方向的内外符合速度残差绝对值在0.5 mm/a 左右，东、北方向的内外符合速度残差中误差均不超过1 mm/a，区域站残差绝对值的最大值超过2.5 mm/a，而CORS 残差绝对值的最大值不超过1 mm/a。总体来看，区域站内符合精度与CORS外符合精度保持一致，福建省三角网反距离加权格网模型东、北方向均能达到1 mm/a 的精度。

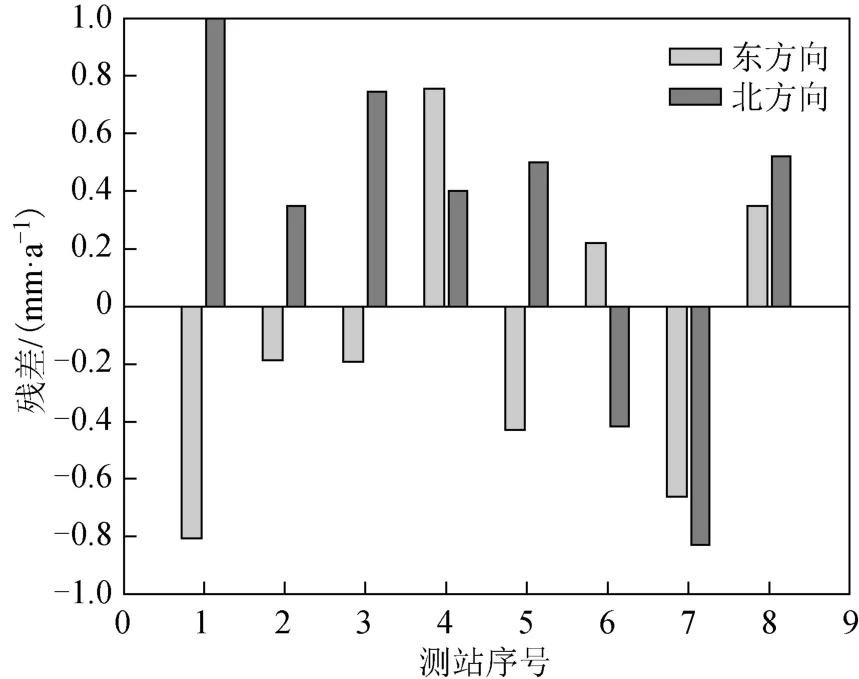
图9 福建省三角网模型CORS 速度场残差柱状图

表3 福建省三角网模型速度场残差统计 单位: mm/a

4 结束语

本文基于福建省及周边区域陆态网测站2011—2017 年长期全球定位系统(global positioning system， GPS）观测数据解算得到福建省区域高精度水平速度场，分别使用68 个区域站和7 个CORS构建和评估福建省区域欧拉矢量块体运动模型和Delaunay 三角网反距离加权格网模型，统计并分析2 种模型的内外符合精度指标，结果表明：

1）福建省及周边区域整体呈现由西北至东南方向的运动趋势，东、北方向整体平均速度分别为32.8、-11.7 mm/a。由于其块体内部构造活动并不剧烈，因此本文使用的2 种模型的精度相当，东、北方向速度场的精度均能达到1 mm/a 左右。

2）相较于欧拉矢量块体运动模型，Delaunay三角网反距离加权格网模型虽然具体物理意义不强，但是在考虑了距离和方位信息（最大化最小角特性）的同时，Delaunay 三角剖分充分利用了每个点的信息，该特性使得采用少量的信息便可以刻画更为精细的局部特征，且使用更为简便，根据格网点速度场可以快速得到该区域内任意未知点的速度值。

与中国大陆整体速度场模型相比，区域速度场模型更加符合局部区域地壳运动特征，因此针对每个地区建立适用自身的高精度水平速度场模型对于现代高精度大地测量工作非常有必要。文中提出的基于Delaunay 三角网的反距离加权格网模型精度高，且计算相对简单，使用较为方便，值得进一步借鉴和推广。