基于问题链的数学微专题设计

【摘 要】在数学微专题中融入问题链教学的理念，通过对“认知冲突链”“思维导向链”“内化提升链”“拓展深入链”的有序设计，进而推动传统课堂的转型，促使学生的学习从“想学”到“学会”“会学”“乐学”的跨越。

【关键词】问题链;微专题;两边夹

【作者简介】吕增锋，中学正高级教师，研究方向为数学教育、微课开发。

【基金项目】浙江省2019年度重点规划课题“精准·自主·深度：基于‘学历案的高中数学微专题教学实践研究”（2019SB051）

数学微专题教学一般运用于高三复习课，虽然与传统的大专题教学相比，微专题教学具有“因微而准、因微而细、因微而深”的优点，但从本质层面分析，微专题其实就是传统习题集或复习材料的“浓缩版”或“精华版”。微专题教学还是依赖于“教师讲，学生练”的陈旧形式，它无法从根本上促使传统课堂的转型与学生学习方式的转变。

引入“问题链”可以有效弥补微专题的不足。一方面，问题链为学生提供了数学学习的框架，使学生能够通过问题链获得较高水平的数学知识;另一方面，问题链中问题间的跨度又为学生的高水平思维提供了无限的可能[1]。在数学微专题设计中，如果能够把问题链有机地融入其中，学生就可以通过问题链驱动学习的进程，实现数学知识的自主探究与思维的自主建构。下面以“两边夹”解题策略微专题为例，浅谈基于问题链的数学微专题设计。

一、设计“认知冲突链”，让学生想学

数学微专题教学不仅能巩固和强化学生已有的解题经验，而且还能让学生获得新的解题技巧，优化解题思维。但由于高三学生已经初步具备了一套“行之有效”的解题策略，如何让已经深受思维定式影响的学生愿意学习并接受新的解题方法是数学微专题设计中首先需要考虑的问题。可以通过制造“认知冲突”来激发学生的学习动机。人都有解决认知冲突的本能，学生一旦发现那些“行之有效”的方法不好用或不能用时，就会促使他们去寻求新的解题方法。

“认知冲突链”的设计可以按照“回忆—尝试—评价—激发”的逻辑主线展开。在学生面对相对陌生的问题时，教师可以先让学生回忆问题的类别，引导学生从已有的认知结构中寻找解题方法，借助已有的解题经验去尝试解题，再对解题过程进行评价，分析原有方法存在的不足，激发学生进一步探索的欲望。

例1 已知函数f（x）=x2-2x-t（t∈R）在区间[0，3]上的最大值为2，则实数t的值为 。

【回忆】教师让学生思考这道题目属于哪类问题，以前是否接触过类似的题目，可以用什么方法来解决。

【尝试】这是一道求函数最值问题的题目，这个函数是由二次函数外加绝对值构成的，其图像呈现“W”型，一般可以通过图像来确定其最值。

学生在解题时需要考虑函数的最大值在什么情况下取得，以及如何确定t的值。

结合图像，其最大值只有在f（0）=t，f（1）=t+1，f（3）=t-3处取得，然后通过逐一验证以确定t的值。

①當fmax（x）=f（0）时，即t=±2，

t=2f（1）=3>2，t=-2f（3）=5>2，所以t=±2不符合题意。

②当fmax（x）=f（1）时，即t=1或t=-3，

t=1f（0）=1，f（3）=2，符合题意;t=-3f（0）=3>2，f（3）=6>2不符合题意。

③当fmax（x）=f（3）时，即t=1或t=5，

t=5f（0）=5>2，f（1）=6>2不符合题意。

综上所述，t=1。

【评价】此题涉及分类讨论，解题过程相对烦琐。解题结束后，教师让学生思考“能否想到这种解法”“对这种解法有什么看法”。

【激发】教师先肯定学生的解题成果，再针对解题过程存在的弊端，激发学生进一步探究的欲望。

二、设计“思维导向链”，让学生学会

费赖登塔尔认为：“教学过程中所教的东西，要让学生感觉一切都是当着学生面发生的，而不是以教条形式灌输的。”波利亚也强调：“要让学生懂得学习的途径，学习任何东西的最佳途径是自己去发现;教师不要立即吐露你的全部秘密，尽量让学生自己找出来。”因此，数学教学的过程其实就是引导学生自主发现的过程。数学微专题教学不应该只是关注解题技巧、方法的落实，而是应该重在通过设计“思维导向链”使学生经历完整的数学发现的过程，从而实现学生学会学习的目的。

“思维导向链”的设计可以按照“提示—回归—迁移—归纳”的逻辑主线展开。首先，通过提示性的语句打破学生的思维定式，让学生知道还存在更好的解题方法;然后，让研究的视角转向学生熟悉的、相对简单的题目上， 从而使学生的思维回归到问题的起点，进而发现新的解题思路;接着，尝试把解题思路迁移到对复杂问题的解决过程中;最后，经过总结分析，归纳解决问题的核心思想方法。

【提示1】如何把“函数f（x）=x2-2x-t（t∈R）在区间[0，3]上的最大值为2”用不等式表示出来？如何去掉绝对值？

（该问题等价于x2-2x-t≤2。去绝对值一般有两种方法：一是两边平方，但这样做运算量比较大;二是根据绝对值的定义直接展开，即-2≤x2-2x-t≤2。）

【提示2】能否把参数t表示出来？

（参数分离后，得到x2-2x-2≤t≤x2-2x+2。）

【提示3】不等式x2-2x-2≤t≤x2-2x+2具有什么内在的意义？

（这是一个表示“恒成立”的不等式。）

【回归】若不等式x2-2x-2≤t在区间[0，3]上恒成立，如何求t的取值范围？

（问题归结为求函数g（x）=x2-2x-2在[0，3]上的最大值，利用二次函数的性质，结合图1，很容易求出gmax（x）=g（3）=1。）

【迁移】如何通过不等式x2-2x-2≤t≤x2-2x+2求t的值？

图1

（maxx2-2x-2≤t≤minx2-2x+2，借助图像，如图1，得到t=1。）

【归纳】解决这个问题的关键是什么？需要用到哪些思想方法？

（去绝对值把问题转换为函数最值问题，通过数形结合思想“夹出”参数的值。）

三、设计“内化提升链”，让学生会学

不经历深度思考，不经历“内化”的解题充其量就是低层次的重复训练，是无法达成“解一题懂一法，会一类通一片”的目标的。内化的过程正是自我反思、自我提高、自我升华的过程。只有经历这个过程才能真正形成属于学生自己的数学思想方法体系，才能实现从“学会”到“会学”的跨越。

“内化提升链”在微专题中处于核心地位，可以按照“运用—优化—提炼—强化”的逻辑主线展开。首先，让学生把初步获得的解题方法大胆地运用到解题中;然后，在实际操作中通过优化解题方法来化解遇到的思维障碍;接着，反思积累解题经验，使解题方法得到进一步的提炼;最后，在教师的激励下逐步形成适用性强、灵活多样的解题策略，强化解题的一般思路。

例2

设a∈R，若x>0时均有[（a-1）x-1]（x2-ax-1）≥0，则实数a的取值为。

【运用】这道题目能否利用上述的解题思路进行解答呢？

图2

问题等价于[a-（1+1x）][a-（x-1x）]≤0在x>0时恒成立，根据“两边夹”思想，实数a的取值“夹在”曲线y=1+1x与y=x-1x之间（如图2），所以a=32。

例3 已知函数f（x）=2x-ax-b（a，b∈R），对任意的x∈[1，2]，均有f（x）≤m，则实数m的最小值为。

【优化1】此题与例1和例2比较有何不同？

（题目中包含多个参数。）

【优化2】对于包含多个参数的式子如何变形比较合理？

（2x-ax-b≤m-m≤2x-ax-b≤m2x-m≤ax+b≤2x+m①。）

【优化3】如何利用“两边夹”思想求①式的m值？

（①式可理解为“两曲线夹一直线”，如图3，设M（1，2-m），N（2，1-m），则直线MN的方程为y=-x+3-m，当直线MN与曲线

y=2x+m相切时m的值最小，联立方程

y=2x+my=-x+3-m

x2+（2m-3）x+2=0，由Δ=0m=3+222。）

图3

【提炼】经过例3的解答，你有什么收获？

（不等式变形是解题的关键，尤其是对包含多个参数的不等式，虽然其变形有多种形式，但要遵循熟悉以及容易作图的原则，最后通过图像“夹”出来。）

【强化】已知f（x）=x2+x-a-3在x∈[-1，1]上的最大值为2，则实数a的值为 。

此题虽然包含了两个绝对值，但万变不离其宗，依然可以用“两边夹”的思想解决。

四、设计“拓展深入链”，让学生乐学

哲学家卡尔·波普尔认为，愈来愈深化的问题，愈来愈能启发新问题。通过对微专题中问题链的探求，学生学会了一种解题方法，会利用相关的思想方法解决一类数学问题，但这并不是微专题教学的终极目标。随着問题链的不断拓展和深入，学生在“发现问题—解决问题—再发现问题”的过程中，思维逐渐走向纵深，形成完整的、具有联系的数学知识体系。

“拓展深入链”可以围绕着“情境拓展”与“方法拓展”两个层面进行。“情境拓展”旨在通过改变问题的条件、结论与类型，让学生进一步感受解题方法的普适性;“方法拓展”是对已有的思想方法作适当的改进以适应新的题型，让学生体会解题方法的灵活性。“拓展深入链”能够为学生带来成就感，使学生从“会学”走向“乐学”。

例4 已知二次函数满足f（1）=2，对于x∈R都有-x-1≤f（x）≤2x2+3x+1，求函数f（x）的解析式。

该题看似与前面的含绝对值的最值问题不是同一类题目，但当把x=-1代入不等式-x-1≤f（x）≤2x2+3x+1后，得到0≤f（-1）≤0，这显然就是“两边夹”思想的直接应用。然后利用f（1）=2，f（-1）=0联立方程即可求出函数f（x）的解析式。

【情境拓展】已知函数f（x）的定义域为R，且对x，y∈R都有f（x+3）≤f（x）+3，f（x+2）≥f（x）+2，若f（1）=2019，则f（2019）=。

两组不等式f（x+3）≤f（x）+3，f（x+2）≥f（x）+2方向相反，可以利用“两边夹”思想建立两个不等式之间的等量关系。

由f（x+3）≤f（x）+3，f（x+2）≥f（x）+2得，f（x）≥f（x+3）-3f（x+1）≥f（x+4）-3≥f（x+2）-1≥f（x）+1;

f（x）≤f（x+2）-2f（x+1）≤f（x+3）-2≤f（x）+1，所以f（x+1）=f（x）+1，f（2019）=f（2018）+1=f（2017）+2=…=f（1）+2018=4037。

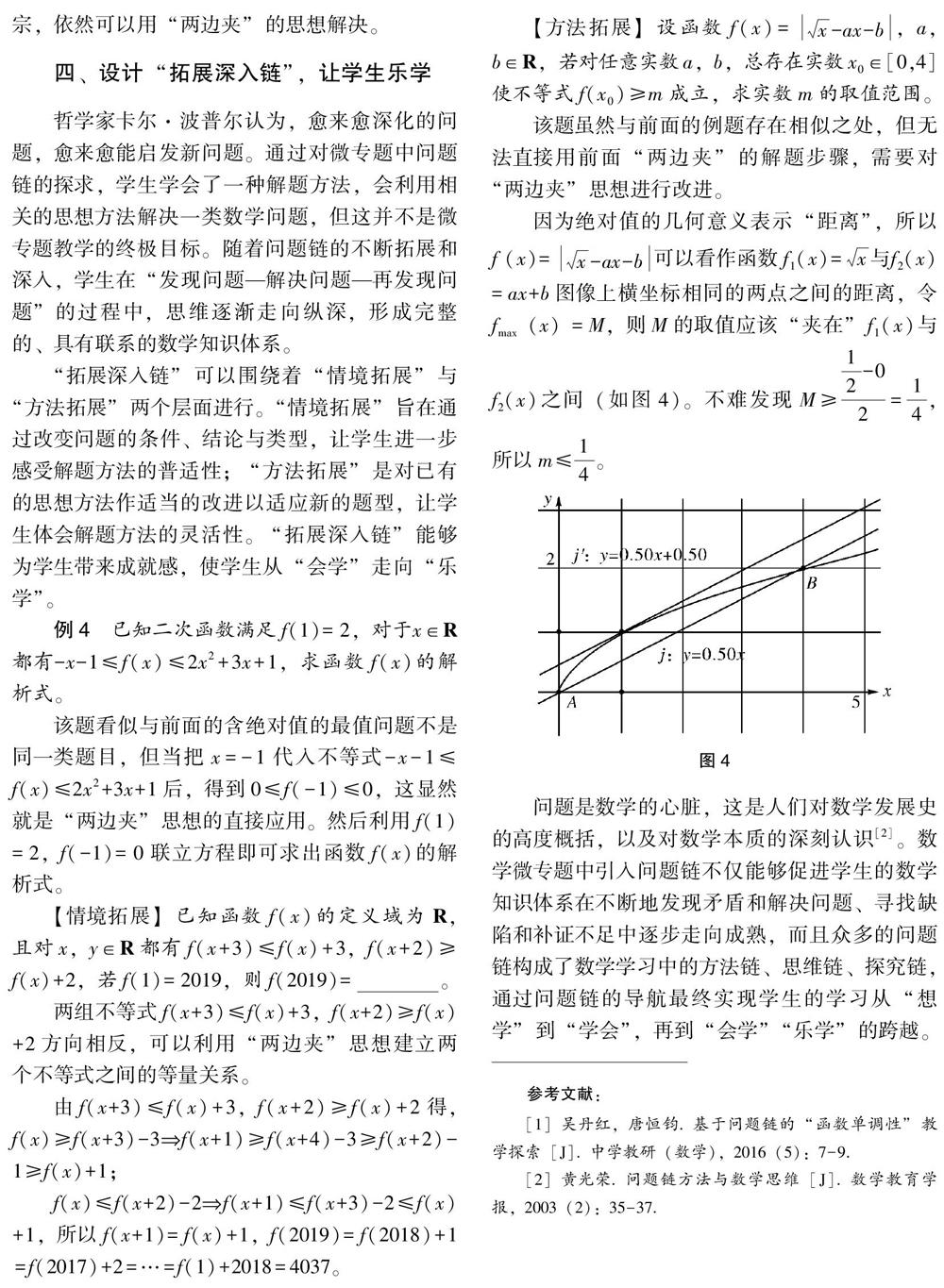
【方法拓展】设函数f（x）=x-ax-b，a，b∈R，若对任意实数a，b，总存在实数x0∈[0，4]使不等式f（x0）≥m成立，求实数m的取值范围。

该题虽然与前面的例题存在相似之处，但无法直接用前面“两边夹”的解题步骤，需要对“两边夹”思想进行改进。

因为绝对值的几何意义表示“距离”，所以f （x）=x-ax-b可以看作函数f1（x）=x与f2（x）=ax+b图像上横坐标相同的两点之间的距离，令fmax（x）=M，则M的取值应该“夹在”f1（x）与f2（x）之间（如图4）。不难发现M≥12-02=14，所以m≤14。

图4

问题是数学的心脏，这是人们对数学发展史的高度概括，以及对数学本质的深刻认识[2]。数学微专题中引入问题链不仅能够促进学生的数学知识体系在不断地发现矛盾和解决问题、寻找缺陷和补证不足中逐步走向成熟，而且众多的问题链构成了数学学习中的方法链、思维链、探究链，通过问题链的导航最终实现学生的学习从“想学”到“学会”，再到“会学”“乐学”的跨越。

参考文献：

[1]吴丹红，唐恒钧.基于问题链的“函数单调性”教学探索[J].中学教研（数学），2016（5）：7-9.

[2]黄光荣.问题链方法与数学思维[J].数学教育学报，2003（2）：35-37.