线性悬臂梁式压电振子的理论分析与仿真

杨晋宁　曹雅莉

摘要：悬臂梁式压电俘能系统的输出电压和功率与压电振子的结构尺寸、外界激振频率等都有着密切的联系。同时，线性压电振子当与环境振动激励产生共振时才能获得最大的输出功率，而其固有频率又与压电振子的结构尺寸等参数有关。因此，为了在实际应用中提高俘能效率，就需要研究这些参数对悬臂梁式压电俘能系统性能的影响规律。现针对悬臂梁式压电振子结构进行了相关的理论分析，并通过COMSOL Multiphysics有限元软件，对系统输出电压和功率受外界激振频率、负载、外激励加速度的影响规律进行了仿真分析，从而为优化悬臂梁式压电振子结构，降低系统固有频率提供了参考。

关键词：压电振子;固有频率;激振频率;负载;仿真

0 引言

自然界中的能源多种多样，其中振动能是一种取之不尽、用之不竭的“绿色能源”，它不像其他能源那样随时受到时间、地域、环境等因素的限制。若能将其转化为电能，有助于解决微电子器件需长期、实时持续的能源供给问题。实际上，利用自然界中的振动给微型发电装置提供动力，可以源源不断地将振动能转变为微机电系统所需要的电能。由于利用正压电效应原理在环境中收集到的振动能具有较高的能量密度、清洁环保、高输出电压和功率以及易于实现结构微型集成化等优点，因而近年来备受关注[1]。在理论研究中，一般将压电式悬臂梁作为压电式振动俘能系统基本结构的等效体，利用线性动力学模型对其进行建模与分析，故常将它称之为线性悬臂梁式压电振子。

本文为了进一步提高能量转换效率，在对悬臂梁式压电振子结构和尺寸进行理论分析的基础上，利用COMSOL Multiphysics软件，将外界激振频率等参数对输出电压和功率的影响进行仿真分析，为优化悬臂梁式压电振子结构提供理论参考。

1 压电能量收集器的理论分析

1.1    基本结构和原理

能量收集器中最典型的结构是悬臂梁式，其具有诸多优点。为进一步提高能量转换效率，使压电结构的固有频率、外界激振频率和负载三者之间有效匹配起来，本文采用基于正压电效应原理下的矩形悬臂梁结构，如图1所示。该结构的中间层是用铜材料制成的金属基体，在基体的上下方各粘有一层很薄的PZT-5H压电陶瓷，利用串联连接的输出方式，构成双晶压电振子，Z轴为极化方向。压电振子的左端固定，另一端放置一个材料为45钢的质量块，用于降低压电结构的固有频率，以便收集外界低频环境中的振动能量。

在外界振动源的激励下，将会激发压电振子进行振动而发生弯曲变形，使上下两片PZT-5H压电陶瓷分别受到拉伸和压缩作用，结合正压电效應原理此时可对外输出电压。该结构采用激励方向与极化方向相垂直的d31振动模式，使其共振频率更低，更易与外界环境产生共振。悬臂梁式压电结构尺寸参数如表1所示。

1.2    固有频率

根据文献[2-3]提出的分布式参数动力学模型，在忽略质量惯性矩和剪切变形影响的前提下，可将线性悬臂梁式压电振子等效为一个Euler-Bernoulli梁，然后利用Euler-Bernoulli方程对其机电耦合行为进行建模。通过理论推导，得到计算各阶固有频率的公式[4]：

式中，E为压电振子的弹性模量;ρ为压电振子的等效密度;l为压电振子的长度;w为压电振子的宽度;h为压电振子的厚度（h=he+2hp）。

由（1）式可看出，压电振子的fi与E、w和h之间呈正比关系，与ρ和l之间呈反比关系。当压电振子的一端放置质量块时，相当于增加了ρ的大小，从而起到降低fi的作用。

2 有限元分析

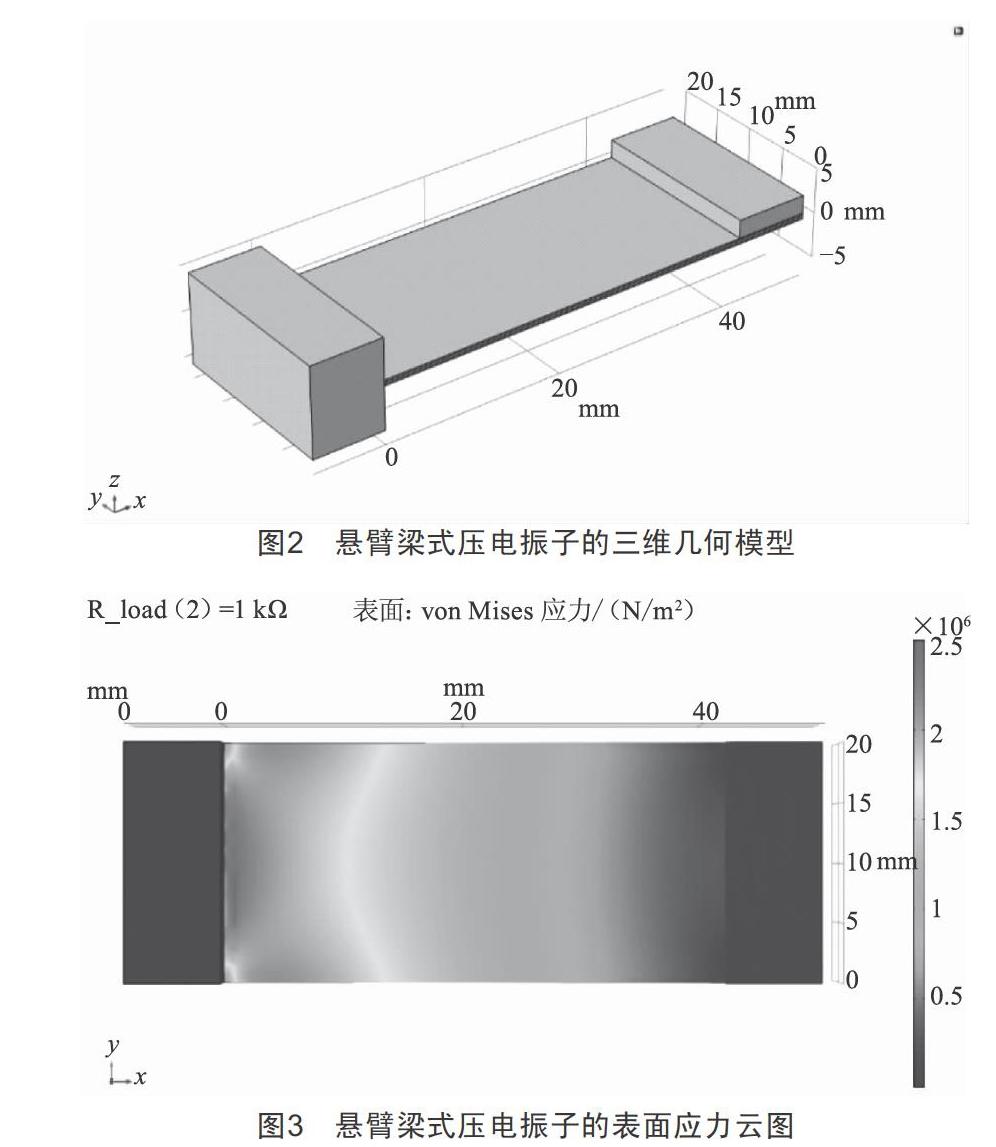
在COMSOL Multiphysics多物理场仿真软件中，按照表1所示数据对悬臂梁式双晶压电振子进行三维建模，如图2所示。通过求解，可以得到压电振子的表面应力云图，如图3所示，σmax位于压电振子根部，为使压电振子产生更多的电能，压电片应粘贴于此处[5]。

2.1    模态分析

对于线性悬臂梁式压电振子而言，其固有频率只有与外界环境产生共振时，才能输出最大电能。利用模态分析不仅能够求解出悬臂梁式压电振子的各阶振型及固有频率，还可以仿真其尺寸参数对固有频率的影响，最终为优化悬臂梁式压电振子结构提供理论依据[6]。悬臂梁式双晶压电振子的前四阶振型模态图及固有频率值，分别如图4和表2所示。

从图4中可看出，除了一阶振型模态图外，其余三阶振型模态图都是非正常的。对于悬臂梁式压电振子而言，一阶振型下应变最大，输出的电能也最多，因此在实际研究中为了建模分析方便，通常只考虑一阶振型下的固有频率值。

2.1.1    振子长度对其一阶固有频率的影响

如表1中，除l外，其余几何参数均不变，使l在30～50 mm按步长为5变化取值，通过仿真求解可得到相对应的f1值分别为196.4 Hz、148.5 Hz、116.74 Hz、94.476 Hz、78.214 Hz。可以看出，随着l的不断增大，f1（一阶固有频率）逐渐减小，二者呈反比关系。这就意味着，增大l可以有效降低f1，但l的增大必须要在一定的范围之内，否则会增大能量收集器的几何尺寸，与其微小集成化的特点相违背。该仿真求解结论与本文前面对公式（1）的理论分析结论相一致。

2.1.2    振子宽度对其一阶固有频率的影响

如表1中，除w外，其余几何参数均不变，使w在10～30 mm按步长为5变化取值，通过仿真求解可得到相对应的f1值分别为77.387 Hz、77.829 Hz、78.214 Hz、78.543 Hz、78.823 Hz。可以看出，f1随w数值的增大而缓慢增大，虽增大幅度很小，但二者仍呈正比关系。总体而言，该仿真求解结论与本文前面对公式（1）的理论分析结论相一致，但是压电振子一阶固有频率受其宽度的影响并不大，基本可忽略不计。

2.1.3    振子压电片厚度对其一阶固有频率的影响

如表1中，除hp外，其余几何参数均不变，使hp在0.1～0.5 mm按步长为0.1变化取值，通过仿真求解可得到相对应的f1值分别为49.94 Hz、78.214 Hz、109.49 Hz、142.43 Hz、176.37 Hz。可以看出，f1随hp数值的增大而增大，二者呈正比关系，该仿真求解结论与本文前面对公式（1）的理论分析结论相一致。

2.1.4    振子质量块质量对其一阶固有频率的影响

如表1中，按照单晶压电振子不带质量块、单晶压电振子带质量块、双晶压电振子不带质量块、双晶压电振子带质量块4个方面，通过仿真求解得到相对应的f1值分别为98.993 Hz、56.453 Hz、142.09 Hz、78.214 Hz。可以看出，不论是单晶压电振子还是双晶压电振子，自由端带质量块都会降低其一阶固有频率，该仿真求解结论与本文前面对公式（1）的理论分析结论相一致。

因此，在实际应用时可以通过增大l、减小hp，同时在压电振子一端放置质量块并加大质量块质量的方法来降低压电振子的一阶固有频率，使悬臂梁压电振子与振动激励源之间产生共振，从而可以收集到环境中的低频振动能量，这种方法非常适用于那些低频小幅的振动环境。

2.2    频率响应分析

由于外界环境的振动频率一般处于0～200 Hz，因此在有限元仿真时对频率范围进行设定，通过扫频的方法使其在60～80 Hz内进行取值，步长为1。同时对压电振子施加一数值为1的正弦外激励加速度，求解后可得到输出电压和功率对频率的响应曲线，如图5所示。从图5中可知，在压电振子的一阶固有频率处具有最大输出电压和最大输出功率。这是由于当压电振子的一阶固有频率与环境外加的加速度频率接近或一致时，压电振子将会产生共振，此时压电振子在外激励作用下发生最大的弯曲变形，根据正压电效应原理，将产生最大的输出电压和输出功率。

2.3    负载对输出电压和功率的影响

由前面的分析可知，本文中压电振子的共振频率就是其一阶固有频率78 Hz，因此将频率设定在78 Hz，仿真求解此压电振子在共振条件下负载对输出电压和功率的影响关系。将负载电阻值在102～105 Ω之间扫描取值，步长为0.25，求解得到负载对输出电压和功率的影响曲线，如图6所示。

由图6可看出，输出功率随负载电阻的增大而迅速增大，在负载电阻为1.78 kΩ时输出功率达到最大值5.18 MW，根据电路理论的推导可以知道，只有当外接电阻与压电振子内电阻相等或接近时，负载才能获得最大电能，因此压电振子内电阻为1.78 kΩ。但当负载电阻继续增大时，外部电路电流将会变得很小，因此输出功率将迅速减小。随着外接负载电阻阻值的增大，输出电压也在增大，当阻值增大到某一数值时，输出电压将保持不变，此时的电压值为7.87 V。

2.4    加速度对输出电压和功率的影响

将频率继续设定在78 Hz，仿真求解此压电振子在共振的条件下外激励加速度对输出电压和功率的影响。将加速度在0.25g～2g扫描取值，步长为0.25，求解得到加速度对输出电压和功率的影响曲线，如图7所示。

在图7中可看出，随着加速度的增大，输出电压和功率均增大，加速度对于输出电压和功率的影响都呈正比关系。但是加速度与输出功率关系近似于一个二次函数，而加速度与输出电压的关系则为线性，可见加速度对于输出功率的影响要大于对输出电压的影响，输出功率与输出电压呈二次方关系。

3 结语

本文對线性悬臂梁式压电振子的结构尺寸参数进行了理论分析，得出了相关结论，并通过有限元软件进行建模、仿真和分析，研究了压电振子的长度、宽度、厚度以及自由端质量块对于其一阶固有频率的影响规律，验证了理论分析的正确性，并对外界激振频率、负载、外激励加速度对输出电压和功率的影响进行了仿真分析，使压电结构的固有频率、外界激振频率和负载三者之间可以有效匹配，为优化悬臂梁式压电振子结构，调整系统固有频率提供了理论依据。

[参考文献]

[1] 王德石，张恺.压电换能器设计原理[M].武汉：武汉理工大学出版社，2016.

[2] ERTURK A，INMAN D J.On mechanical modeling of cantilevered piezoelectric vibration energy harvesters[J].Journal of Intelligent Material System and Structures，2008，19（11）：1311-1325.

[3] ERTURK A，INMAN D J.A distributed parameter electrome-

chanical model for cantilevered piezoelectric energy harvesters[J].Journal of Vibration and Acoustics，2008，130（4）：1-10.

[4] 邓冠前.基于压电陶瓷的振动能量捕获关键技术研究[D].长沙：国防科技大学，2008.

[5] 袁秋洁.基于压电材料的振动能量收集理论及其结构分析[D].北京：华北电力大学，2009.

[6] 陈仲生.压电式振动能量俘获理论与方法[M].北京：国防工业出版社，2017.

收稿日期：2020-04-10

作者简介：杨晋宁（1984—），男，山西乡宁人，硕士，讲师，研究方向：先进制造技术。