离心压缩机齿轮参数化造型、啮合装配及动力学仿真分析
2020-10-21林伟伟

摘要:介绍了在Pro/E软件环境下,引入坐标变换矩阵和离散变量实现圆柱齿轮的三维参数化造型,并结合啮合理论进行精确装配。同时,基于多体动力学软件MSC.ADAMS对齿式离心压缩机的齿轮轮系进行动力学仿真分析,进而验证造型和装配的准确性。
关键词:圆柱齿轮;参数化;啮合理论;动力学仿真
0 引言
齿轮作为传递运动和动力的基础元件,在工业发展中发挥着十分重要的作用。齿轮造型及精确啮合装配是齿轮加工和对齿轮进行各种运动、动力等分析的基础,模型的准确性会直接影响到齿轮的加工精度和分析结果。圆柱齿轮包括直齿渐开线齿轮、斜齿渐开线齿轮、变位齿轮等。齿轮的参数化造型过程实际上就是解决变位斜齿轮造型的过程,当变位系数为0时它就是标准齿轮,当螺旋角为0时它就是直齿轮。
为拓展数字化研究领域,本文对圆柱齿轮参数化造型、啮合装配及动力学仿真进行研究。基于Pro/E完成渐开线变位斜齿轮的参数化造型,实现齿轮的自动化设计,同时结合齿轮啮合原理,添加装配辅助参照,实现变位斜齿轮的精确啮合装配,最后基于ADAMS完成齿式离心压缩机齿轮轮系的运动学和动力学仿真分析,验证齿轮参数化造型和啮合装配的准确性。
1 参数和造型
齿轮参数化造型的难点主要是变位齿轮齿厚的计算、斜齿轮的旋向问题以及螺旋线生成等。目前齿轮造型的方法有很多,但这些关键问题都没有很好的解决手段,比如针对斜齿轮,通常是分别建立左旋和右旋两个基本参数化模型。本文在学习前人研究成果的基础上,提出基于Pro/E的圆柱齿轮参数化建模,解决以上几个齿轮参数化造型的关键问题。
齿轮的基本参数如表1所示。
1.1 渐开线和齿形角度关系
图1为渐开线的形成原理,其方程为:
Pro/E具有强大的曲线方程功能,可通过渐开线方程生成齿轮轮齿的渐开线齿廓,进而通过扫描或扫描混合生成轮齿。在Pro/E齿轮造型过程中,相对于扫描命令,使用扫描混合命令可准确生成轮齿,且保证轮齿两端面与齿宽平面完全对齐。扫描混合命令生成轮齿至少需要两个齿廓截面的草绘,因此需依次建立四条渐开线齿廓,如图2中的渐开线1、2、3、4。四条渐开线分属不同的坐标系,为了在Pro/E的缺省坐标系XOY同时表达这四条渐开线,曲线生成过程需要进行坐标转换。一种方法是在Pro/E中分别新建四个坐标系,输入坐标旋转角度和平移位移,然后分别基于各自的坐标系生成四条渐开线;另一种方法是通过坐标变换矩阵,将四条渐开线所在的坐标转换到缺省坐标系,进而各自生成渐开线。
以上两种方法都需要准确计算渐开线的旋转角及移动位移。下面根据齿轮啮合理论推导计算渐开线坐标变换的角度关系。
根据图1、图2,在变位齿轮中:
将θ和γ的关系式分别写入Pro/E的关系中。
根据坐标转换(图2),渐开线1到缺省坐标系XOY的变换矩阵为:
渐开线1在缺省坐标系XOY下的方程为:
在Pro/E中制作齿廓渐开线采用方程式的方法精确生成,选缺省坐标系,在文件rel.ptd中输入:
其中t为参变量,它在0到1之间变化,本文中t意义相同。
渐开线3到缺省坐标系XOY的变换矩阵为:
渐开线3在XOY坐标下的方程为:
渐开线2、4类似,这里不再重复。
1.2 螺旋线
目前创建螺旋线的方法通常是在基准平面内创建一条角度为螺旋角的斜线,然后投影到分度圓曲面得到螺旋线。这种方法创建过程繁琐,且引入一个冗余的分度圆曲面。本文通过螺旋线形成的分析,采用方程直接绘制螺旋线。螺旋线是柱面x2+y2=r2和z=x/tan β的交线,所以螺旋线方程应为:
1.3 螺旋方向
决定斜齿轮旋向的参数是螺旋角β和螺旋齿的坐标旋转角γ。在Pro/E关系式中,这两个角都不允许直接输入负值。为此,本文绕开正负角度,通过两种方法分别解决这两个问题。
斜齿轮旋向是由螺旋角β的正负引起螺旋线方向的变化,在不改变螺旋角的情况下,引入一个离散参数k,通过k控制螺旋线的x坐标,进而控制螺旋线方向。修订Pro/E中螺旋线方程如下:
螺旋齿的坐标旋转角γ无法反向偏移,可在Pro/E关系中引入判断语句:
1.4 建模步骤
在Pro/E参数化造型之前一定要统一单位,特别是角度和弧度。齿轮的参数化建模基本步骤如下:
(1)新建一个Pro/E零件,在工具—程序—编辑文本内添加输入的参数。
(2)创建基圆、分度圆、齿顶圆、齿根圆,将尺寸代号进行参数化。根据齿轮参数关系,在关系窗口内定义各参数的关系式。
(3)通过方程绘制螺旋线,并在水平基准面捕捉螺旋线的投影曲线,注意基准和方向的统一。
(4)通过方程绘制渐开线齿廓,并通过坐标旋转变换绘制其他齿廓。
(5)使用扫描混合命令选取螺旋线和其投影线,定义螺旋线两端点的草绘,通过捕捉渐开线轮廓以及齿顶圆、齿根圆,并进行齿根倒圆角,完成轮齿齿形草绘,进而扫描混合出轮齿实体。扫描混合过程中要注意两条轨迹线的选取顺序及草绘平面与轨迹线的垂直关系。
(6)阵列轮齿。
齿轮的参数化建模如图3所示。
2 啮合装配
2.1 正确啮合条件
平行轴斜齿轮在端面内的啮合相当于直齿轮的啮合,所以其正确啮合的条件为端面模数及端面压力角相等,两基圆柱螺旋角必须相等,于是得到平行轴斜齿轮正确啮合条件:
因外啮合齿轮的螺旋角大小相等,方向相反,而内啮合时方向相同,故式中负号用于外啮合,正号用于内啮合。
2.2 啮合装配方法
在标准齿轮啮合和等变位齿轮啮合中,由于啮合角等于分度圆压力角,故标准中心距为:
而在非等变位齿轮啮合中,啮合角并不等于分度圆压力角,此时,啮合角为:
对于斜齿轮,取端面模数、端面压力角。
在确定中心距之后,齿轮接触齿面之间的啮合至关重要。在Pro/E齿轮装配过程中,对于接触曲面复杂的变位斜齿轮,精确啮合装配需添加辅助参照。本文结合齿轮啮合理论,提出三种精确啮合装配方法。
方法一:对于无齿侧间隙的齿轮啮合,只需分别建立过齿槽和齿厚的基准平面,装配时令两基准面重合即可保证准确啮合。该方法比较简便,但适用范围有限,主要适合标准齿轮和等变位齿轮。
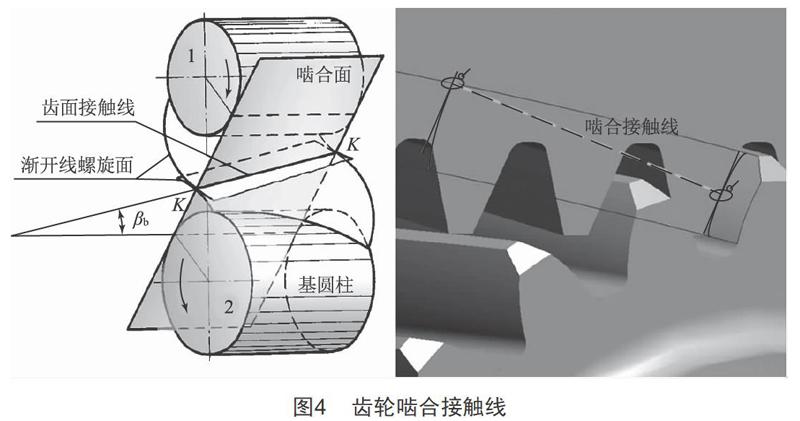
方法二:斜齿轮在啮合过程中总是从端面齿廓的一点进入啮合,从齿面的某一位置退出啮合。结合齿面接触线特点,在装配过程中,根据齿轮参数在齿面上准确绘制其中一条接触线,令该接触线在另一配合齿面内,模拟齿轮啮合以实现精确装配,如图4所示。
方法三:齿轮啮合过程中,端面啮合齿廓总是存在若干相切的位置。根据该啮合特点,在装配过程中,定义配合齿轮端面齿廓曲线的凸轮接触,即可确定齿轮某一时刻精确啮合装配位置。该方法操作简便,且适用于所有齿轮啮合装配。
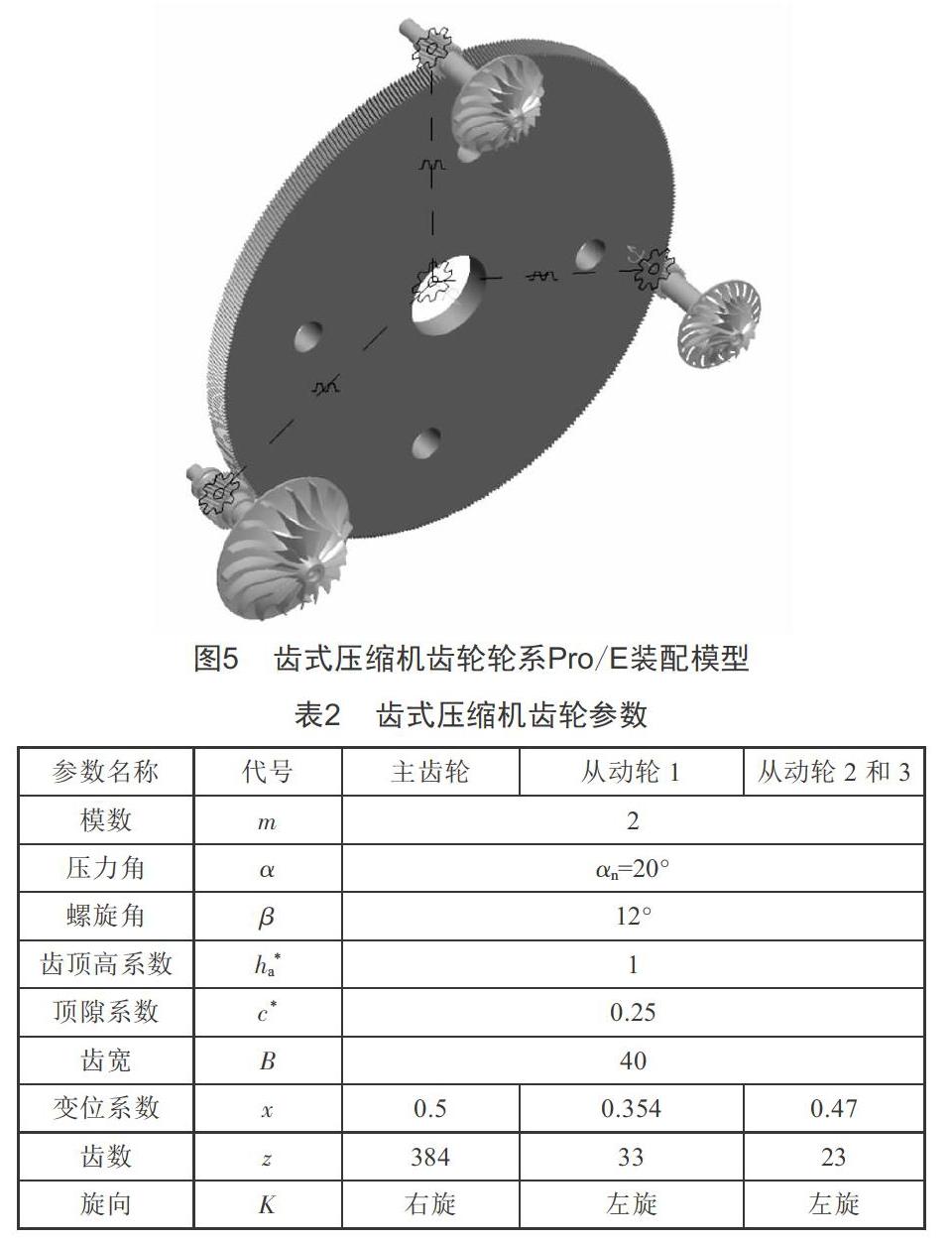
以上三种齿轮精确啮合装配方法都引入了辅助参照,在准确定义某一啮合位置后,配合齿轮间添加齿轮约束,设置传动比,然后删除辅助装配参照,即实现了齿轮的精确装配。图5为齿式离心压缩机齿轮啮合装配。
3 动力学仿真
结合齿轮参数化造型方法和啮合装配,本文针对齿式离心压缩机轮系进行参数化建模和啮合装配,并基于ADAMS进行运动学和动力学仿真分析。齿式压缩机齿轮参数如表2所示。
3.1 模型及运动约束
齿轮轮系模型导入ADAMS后,添加运动副、转速、载荷,如图6所示。
结合齿式压缩机传动,在主动轮gear0施加转速17 850 r/s,从动轮gear1施加6.002 2×105 Nmm(600.22 Nm)的负载力矩,从动轮gear2、gear3施加1.075 27×106 Nmm(1 075.27 Nm)的负载力矩。为防止负载施加过程陡变,采用STEP函数加载,使力矩在一段时间内平稳加到恒定值,即STEP(time,0,0,0.01,
600 220)。图7为三个从动轮的负载力矩加载曲线,红色曲线为从动轮gear1的加载过程,粉色和蓝色重叠曲线为从动轮gear2、gear3的加载过程。
3.2 齿轮接触碰撞力
齿轮传递转速和扭矩主要是通过轮齿之间的接触碰撞。在ADAMS中,选用基于Impact函数的接触力,Impact是用刚度系数和阻尼系数来计算接触力的。轮齿碰撞所引起的冲击力,可以作为两个变曲率半径柱体撞击问题。根据Hertz碰撞理论,考虑接触面积为圆形时:
由此式可得到碰撞时接触法向力P和变形δ关系为:
公式中K取决于碰撞物体材料和形状:
式中:R1、R2为接触物体在接触点的接触半径,齿轮接触近似以分度圆半径代替接触点的当量半径。
式中:μ1、μ2为接触物体材料的泊松比;E1、E2为接触物体材料的弹性模量。
齿轮材料都是17CrNiMo6,其泊松比为0.3,弹性模量为2.06×105 N/mm2。
主齿轮gear0和从动轮gear1,代入数据计算得:
主齿轮gear0和从动轮gear2、从动轮gear3接触参数一样,代入数据计算得:
另外,碰撞指数e用来计算瞬时法向力中材料刚度项贡献值,通常取1.5;材料阻尼系数c取50 N/mms,全阻尼穿透值d取0.05 mm;由于两齿面充分润滑,动摩擦系数取0.03,静摩擦系数取0.05。将以上接触碰撞的参数计算结果输入,即完成齿轮碰撞参数设置。
3.3 仿真结果分析
设置仿真时间t=0.02 s,step=4 000进行计算。
图8为轮系各齿轮转速曲线,从图中可以看出,从动轮在主动轮的碰撞冲击作用下,转速逐渐变大,且很快趋于平稳。
通过测量,从动轮gear1的稳定转速平均值为2.077 11×105 rad/s,从动輪gear2的稳定转速平均值为2.979 95×105 rad/s,从动轮gear3的稳定转速平均值为2.979 73×105 rad/s。
从动轮gear1的理论转速为:
从动轮gear2、gear3的理论转速为:
转速误差为:
可见,在误差范围内,轮系的转速满足实际工况。
图9为轮齿之间接触碰撞力曲线,从图中可以看出,在轮齿啮合初期,轮齿由于负载的作用,碰撞力较大,随着传动的平稳,碰撞力也逐步趋于平稳,且在一个稳定的范围内变化。
齿轮在啮合过程中啮合碰撞并不是保持不变的,而是每啮合入一个齿就产生一个脉冲力,且从进入啮合到退出啮合的过程中,啮合力有一个波动。啮合力的波动幅值大小与齿型的结构密切相关,同时,由于应力变形和热膨胀等影响,啮合力大小有可能存在阶跃。因此,为了改善齿轮传动,延长使用寿命,齿轮轮齿需要进行相应的修型处理。
由以上转速和接触碰撞力的仿真结果可知,齿轮轮系的运动学和动力学仿真结果比较准确,具有一定的现实指导意义。同时,齿轮的运动仿真也验证了齿轮的参数化造型方法和啮合装配的准确性。
4 结语
本文结合目前齿轮参数化造型和精确装配存在的问题,引入渐开线坐标变换矩阵、螺旋线方程表达式、螺旋方向判断变量以及啮合装配等,提出基于Pro/E的圆柱齿轮参数化造型和精确啮合装配,解决齿轮造型和装配存在的难题。同时,使用研究方法针对齿式离心压缩机齿轮组件进行参数化建模和啮合装配,并基于ADAMS进行轮系的运动仿真,仿真结果验证了齿轮参数化造型和啮合装配的准确性。
[参考文献]
[1] 濮良贵,纪名刚.机械设计[M].7版.北京:高等教育出版社,2003.
[2] YE Z H,LAN Z H,SMITH M R.Mechanisms and machine theory[M].Beijing:Higher Education Press,2001.
[3] 朱学文,朱国文,何小新.斜齿轮的参数化建模与动力学分析[J].机械传动,2006,30(2):32-33.
[4] 周炎强,杨洁明,田英.基于ADAMS的齿轮动力学特性分析[J].机械工程师,2008(6):99-100.
收稿日期:2020-05-15
作者简介:林伟伟(1983—),男,福建莆田人,硕士研究生,工程师,研究方向:机械。
