试析分类讨论在“圆”教学中的运用

胡定祥

摘;要：初中数学思想中的分类讨论思想，就是将研究的数学对象分成若干类，并对各类情况进行讨论，达到解决问题的一种数学方法。分类讨论时，要做到不重不漏，并保证解答的完整性。本文对"圆"中分类讨论思想，结合例题加以分析。

关键词： 分类讨论;位置关系; 数学对象;教学运用

圆是非常美的几何图形，既是轴对称图形，又是中心对称图形，还具有旋转不变性，这给学生带来了许多思考，从而提高学生的思维能力。

新课标指出：“通过义务 教育阶段的数学学习，学生能够获得适应未来社会生活和进一步发展所必需的重要数学知识（包括数学事实、数学活动经验）以及基本的数学思想方法和必要的应用技能”。所以在数学教学中有效地渗透，培养数学思想方法，已逐渐成为数学课改的热点。数学思想，是指人们对数学科学研究的本质及规律的理性认识。初中阶段常见的数学思想包括：函数与方程思想、化归转化、分类讨论思想、数形结合思想等。其中分类讨论思想是初中数学中最常见、最重要的一种数学思想。

一、分类讨论思想的概念

分类讨论思想是一种最基本的解决问题的思维策略，就是把要研究的数学对象按照一定标准划分为若干不同的类别，然后逐类进行研究，求解的一种数学解题思想。

二、引起分类讨论的主要原因：

分类讨论是比较数学对象的共同性和差异性，根據数量关系或空间形式的某一标准将数学对象分为不同种类，然后分别对它们进行讨论，得出结论的数学思想方法。产生的原因有：

（1）概念本身是分类定义的（如绝对值概念）;

（2）公式、定理、性质和法则有范围或条件限制;

（3）题设的数量大小或关系确定，而图形的位置或形状不确定;

（4）题目的条件或结论不唯一;等。

三、解答分类讨论型问题的步骤

解决分类讨论型问题，需要具备扎实的基础知识，和灵活的思维方式，对问题进行全面衡量、统筹兼顾，切忌以偏概全。

一般步骤为：

（1）确定分类对象;

（2）对问题中的某些条件进行分类;

（3）逐类进行讨论;

（4）对各类讨论结果进行归纳，并加以整合，得出结论。

四、分类讨论思想在初中数学教学中的应用举例

初中数学教学中渗透着分类讨论思想。应用分类讨论思想解题对学生的能力要求较高，在课堂教学中渗透、提炼，还要加强训练。

1.点与圆的位置关系不唯一性

例1.若⊙O所在平面内一点P到⊙O上的点的最大距离为a，最小距离为b（a>b），则此圆的半径为（   ）。

分析：点P可能在圆内，也可能在圆外;如图1、如图2

易知，选（C）。

例2. 过不在⊙O上的一点A，作⊙O的割线，交⊙O于B、C，且AB·AC=64，OA=10，则⊙O的半径R为___________。

分析：点A与⊙O的位置关系有两种：

（1）点A在⊙O内，如图1，延长AO交⊙O于F，由相交弦定理易得：

（2）点A在⊙O外，如图2，由割线定理易得：

故⊙O的半径R为或6。

2.由圆心与弦的位置关系引发多解

例3.已知中，弦，

且AB=6cm，CD=8cm，半径为。求之间的距离。

分析：在半径为的圆中，平行弦的位置关系有如图5和图6两种情形：

易得：弦AB、AC之间的距离为7cm或1cm

3.圆心与角的位置

例4. 在半径为1的⊙O中，弦AB、AC的长分别为和，则∠BAC的度数是____________。

分析：圆心O与∠BAC的位置关系有两种;

当圆心在∠BAC内部时，如图7，

易得 ∠BAC=75°

当圆心O在∠BAC的外部时，由轴对称性可知：∠BAC=15°

所以∠BAC为75°或15

例5. 半径为1的圆中有一条弦，如果它的长为，那么这条弦所对的圆周角的度数等于___________。

分析：弦所对的圆周角有两种情况：

（1）当弦所对的圆周角的顶点在优弧上时，其圆周角为60°;

（2）当弦所对的圆周角的顶点在劣弧上时，其圆周角为120°。

故应填60°或120°。

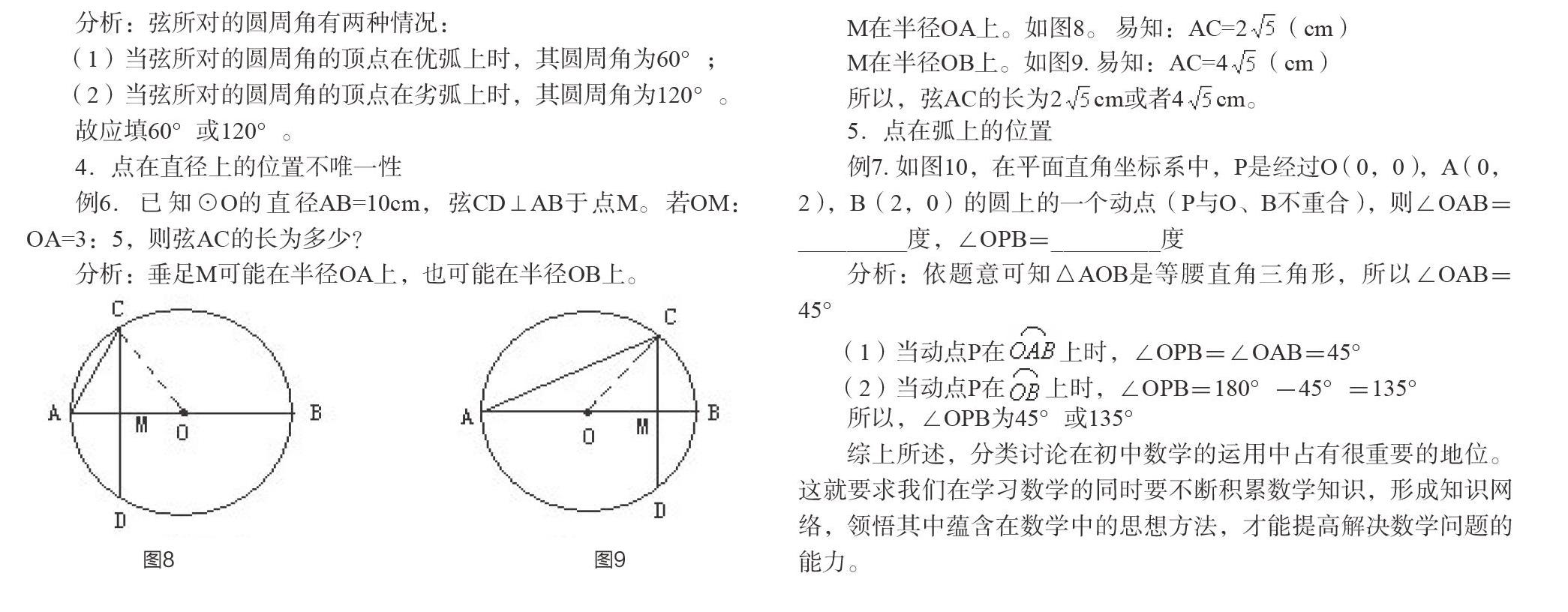
4.点在直径上的位置不唯一性

例6.已知⊙O的直径AB=10cm，弦CD⊥AB于点M。若OM：OA=3：5，则弦AC的长为多少？

分析：垂足M可能在半径OA上，也可能在半径OB上。

M在半径OA上。如图8。 易知：AC=2（cm）

M在半径OB上。如图9. 易知：AC=4（cm）

所以，弦AC的长为2cm或者4cm。

5.点在弧上的位置

例7. 如图10，在平面直角坐标系中，P是经过O（0，0），A（0，2），B（2，0）的圆上的一个动点（P与O、B不重合），则∠OAB=_________度，∠OPB=_________度

分析：依题意可知△AOB是等腰直角三角形，所以∠OAB=45°

（1）当动点P在上时，∠OPB=∠OAB=45°

（2）当动点P在上时，∠OPB=180°-45°=135°

所以，∠OPB为45°或135°

综上所述，分类讨论在初中数学的运用中占有很重要的地位。这就要求我们在学习数学的同时要不断积累数学知识，形成知识网络，领悟其中蕴含在数学中的思想方法，才能提高解决数学问题的能力。