分层演化算法研究

黄友亮

摘  要：演化计算是一种以自然选择理论为灵感，利用简单的编码技术来描述复杂的数据结构，并通过编码表示进行遗传操作和自然选择来引导学习和搜索的方向的计算机科学算法。本文就演化计算的研究背景、分类和特点进行讨论，并对分层演化算法进行初步的探究。

关键词：演化计算;分层演化

一、演化计算的概述

1.1、演化计算的研究背景

演化计算^[1]是基于这个想法发展起来的一种普遍的问题解决方法。它使用简单的编码技术来描述各种复杂的结构，并通过简单的编码表示进行遗传操作和自然选择来引导学习和搜索的方向。用种群组织搜索的方式，使得演化算法特别适合于大规模并行。演化算法具有很高的效率、简单、易于操作和通用性强的特征，这也是演化算法在国际研究领域影响力越来越大的因素。

1.2、演化计算的分类

1.2.1遗传算法

20世纪60年代中期，美国Michigan大学的John.Holland提出了串編码技术，以解决计算机科学与进化论结合的问题，这种编码既适合于变异又适合于交配操作，并正式命名为遗传算法^[2]。遗传算法从一个种群开始，种群代表问题的潜在解集，由经过基因（gene）编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。染色体即多个基因的集合，是遗传物质的主要载体，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现。

1.2.2演化策略

早期的演化策略包括（1+1）策略和（μ+1）演化策略。它们的相似之处是每次只产生一个后代。为了进一步提高效率，后来发展为（μ+λ）演化策略和（μ，λ）演化策略，并引入了重组操作，即由两个个体按类似于杂交的方式生成一个个体。（μ+λ）演化策略根据中群内的μ个个体产生λ个个体，然后将这μ+λ个个体进行比较，选取其中μ个最优者。（μ，λ）演化策略则是在新产生的λ（>μ）个个体中选择μ个最优者。这两种演化策略中的选择方法分别被称为（μ+λ）选择和（μ，λ）选择。

1.2.3、演化规则

在演化规则中，通常将模拟环境表示成有限字符序列中的符号组成的序列。那么问题变成根据观察序列的符号的反应获得最大的收益。演化规则中常用有限态自动机（finitestatemachine，FSM）来表示这样的策略，这么说，就在此时此刻，如何设计有效的FSM将成为战略问题。L.J.Fogel借这种思想对一群FSM进化来获得更好的全局。他们应用得到的数据进行数据诊断、模式识别和分类以及控制系统的设计等方面，取得了良好效果。后来，D.B.Fogel通过演化策略的方法，并应用于演化规则的发展，并应用到神经网络训练及数值优化等领域。

1.3、演化计算的特点

1.3.1、智能性

演化计算智能包括自组织、自适应和自学习，应用的演化计算解决问题中，在确定了编码算法和遗传算子、适应度函数后，利用演化过程中获得的信息自动组织搜索。这种具有自适应、自组织的演化算法，给了它发现环境变化的特点和规律的能力。

1.3.2本质并行性

演化计算的本质并行性具体表现在两个方面：一是演化计算的并行是内在的，即演化算法本身非常适合大规模的并行，而且对其并行效率没有太大的影响;二是演化计算的内涵并行性，由于演化计算是采用种群的方式进行组织搜索，因此可以同时搜索解空间的多个区域，关键是可以相互交流信息。

1.3.3过程性

演化计算通过自然选择和遗传操作等自组织行为来增强群体的适应性。算法模拟的是一个过程。算法的实施也是一个过程，在这个过程中，算法本身无法判定个体处在解空间的位置，因而需要人为干预（即实现确定终止准则）才能终止。

1.3.4多解性

由于演化计算采用种群的方式组织搜索，它从多个点出发，通过这些点内部结构的调整和重组形成新的点，因而算法每次都将提供多个近似解，这对多目标搜索或需要多个近似解作为参照的情况非常有用。

二、分层演化算法

分层演化算法最初由Tang，Man，Kwong，&Liu于1998年提出。HEA可以认为是遗传算法的一种变形，它们都是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是通过模拟自然进化过程搜索最优解的方法。

二者都是从一个种群开始，种群代表问题的潜在解集，由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。在算法一开始，我们就需要实现从表现型到基因型的映射，也就是编码工作。编码通常有浮点数编码和二进制编码等方式。

当第一代的种群产生以后，算法将依照生物学中优胜劣汰的原理，逐代演化从而产生出越来越好的近似解。每一次迭代称为一代，新的一代的产生，都要进过一下三个步骤：（1）计算：在父代中的每一个个体都通过适应值评价函数计算得到适应值;（2）选择：适应值高的个体将被选择，成为新一代的个体;（3）交配：通过交叉、变异等遗传操作来产生新的个体。以上三个步骤不断地循环操作，指导问题得到最优解或者满足终止条件。最后一代种群中的最优个体经过解码后，可以作为问题的近似最优解。

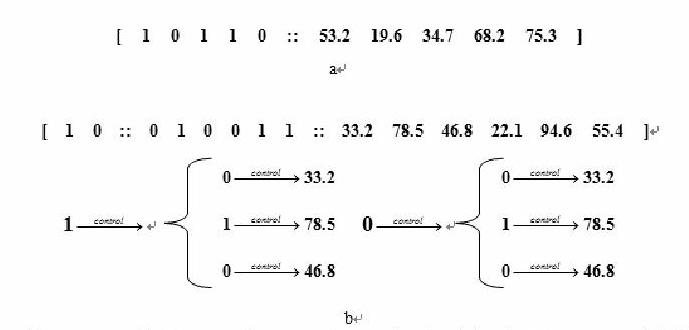
从生物学和医学的观点上看，染色体中的基因结构是各种不同的基因按照分层的结构排列着的，根据这个事实，Tang在1998年提出了分层演化算法（HEA）来模拟这个现象。如果一个控制基因的值是“1”，表示与它对应的参数基因是可用的;如果是“0”，则表示与它对应的参数基因不可用。图1给出了两个分层染色体结构的例子。图1a是一个具有双层基因结构的染色体结构为[控制基因：参数基因]，每一个控制基因对应一个参数基因。其中，基因53.2，34.7，68.2是活跃的，19.6和75.3是不活跃的。图1b表示的是一个具有三层基因结构的染色体，它有两层的控制基因结构为[一层控制基因：二层控制基因：参数基因]。参数基因被第二层控制基因直接控制，而第二层控制基因被第一层控制基因控制，因此，只有基因78.5是活跃的。

尽管现在大多数研究的遗传算法的染色体都是固定长度的，也有很多研究是围绕着具有可变长度的染色体或者其他结构的染色体的遗传算法展开的。从某种程度上来说，HEA可以算是一种可变长度染色体的简明的表现形式。无论如何，通过这种分层的结构，不仅可以简化简单的遗传算法的重新排列，而且在算法的鲁棒性和参数的设置上都有所改进。对于具有分层结构的问题，HEA可以很自然地通过它的特点对问题的参数进行编码，因此，它的这种灵活的表示对于求解一些具有限制的问题时，具有一定的优势。相比起遗传算法，HEA更适合解决聚类问题。

参考文献

[1]  高柯夫.演化计算的应用研究[N].武汉生物工程学院学报.2007.3（3）.

[2]  周明，孙树栋.遗传算法原理与应用[M].北京：国防工业出版社.1999：6.